
Date: 2019-12-25 21:46:07 CET, cola version: 1.3.2
Document is loading... 
All available functions which can be applied to this res_list object:
res_list
#> A 'ConsensusPartitionList' object with 24 methods.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows are extracted by 'SD, CV, MAD, ATC' methods.
#> Subgroups are detected by 'hclust, kmeans, skmeans, pam, mclust, NMF' method.
#> Number of partitions are tried for k = 2, 3, 4, 5, 6.
#> Performed in total 30000 partitions by row resampling.
#>
#> Following methods can be applied to this 'ConsensusPartitionList' object:
#> [1] "cola_report" "collect_classes" "collect_plots" "collect_stats"
#> [5] "colnames" "functional_enrichment" "get_anno_col" "get_anno"
#> [9] "get_classes" "get_matrix" "get_membership" "get_stats"
#> [13] "is_best_k" "is_stable_k" "ncol" "nrow"
#> [17] "rownames" "show" "suggest_best_k" "test_to_known_factors"
#> [21] "top_rows_heatmap" "top_rows_overlap"
#>
#> You can get result for a single method by, e.g. object["SD", "hclust"] or object["SD:hclust"]
#> or a subset of methods by object[c("SD", "CV")], c("hclust", "kmeans")]
The call of run_all_consensus_partition_methods() was:
#> run_all_consensus_partition_methods(data = mat, mc.cores = 4, anno = anno)
Dimension of the input matrix:
mat = get_matrix(res_list)
dim(mat)
#> [1] 31632 79
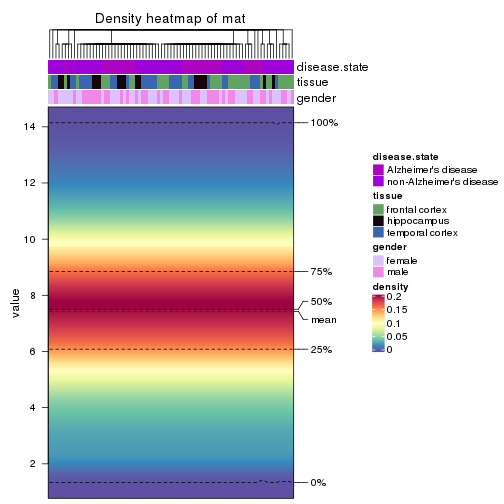
The density distribution for each sample is visualized as in one column in the following heatmap. The clustering is based on the distance which is the Kolmogorov-Smirnov statistic between two distributions.
library(ComplexHeatmap)
densityHeatmap(mat, top_annotation = HeatmapAnnotation(df = get_anno(res_list),
col = get_anno_col(res_list)), ylab = "value", cluster_columns = TRUE, show_column_names = FALSE,
mc.cores = 4)
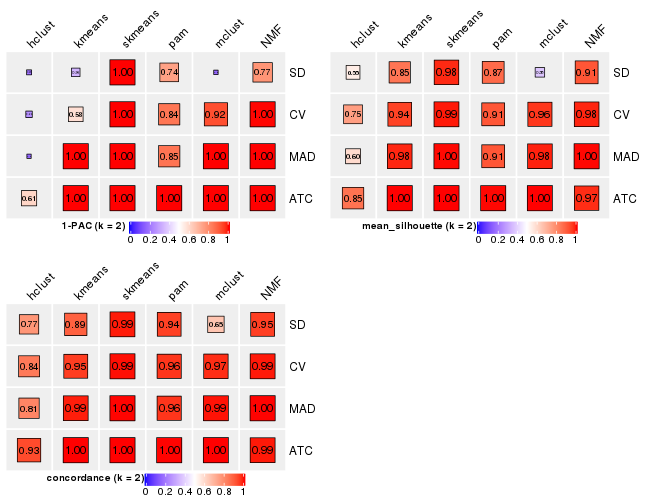
Folowing table shows the best k (number of partitions) for each combination
of top-value methods and partition methods. Clicking on the method name in
the table goes to the section for a single combination of methods.
The cola vignette explains the definition of the metrics used for determining the best number of partitions.
suggest_best_k(res_list)
| The best k | 1-PAC | Mean silhouette | Concordance | Optional k | ||
|---|---|---|---|---|---|---|
| SD:skmeans | 2 | 1.000 | 0.975 | 0.988 | ** | |
| CV:skmeans | 2 | 1.000 | 0.989 | 0.994 | ** | |
| MAD:kmeans | 2 | 1.000 | 0.979 | 0.986 | ** | |
| MAD:skmeans | 2 | 1.000 | 0.997 | 0.999 | ** | |
| MAD:mclust | 2 | 1.000 | 0.983 | 0.993 | ** | |
| MAD:NMF | 2 | 1.000 | 0.998 | 0.999 | ** | |
| ATC:kmeans | 2 | 1.000 | 1.000 | 1.000 | ** | |
| ATC:mclust | 2 | 1.000 | 1.000 | 1.000 | ** | |
| ATC:NMF | 2 | 1.000 | 0.972 | 0.989 | ** | |
| CV:NMF | 2 | 0.998 | 0.980 | 0.989 | ** | |
| ATC:pam | 5 | 0.950 | 0.941 | 0.972 | ** | 2,3,4 |
| CV:mclust | 2 | 0.922 | 0.959 | 0.972 | * | |
| ATC:skmeans | 5 | 0.916 | 0.890 | 0.937 | * | 2 |
| MAD:pam | 2 | 0.849 | 0.909 | 0.962 | ||
| CV:pam | 2 | 0.845 | 0.909 | 0.962 | ||
| SD:NMF | 2 | 0.773 | 0.909 | 0.948 | ||
| SD:pam | 2 | 0.742 | 0.869 | 0.945 | ||
| ATC:hclust | 2 | 0.608 | 0.851 | 0.930 | ||
| CV:kmeans | 2 | 0.584 | 0.943 | 0.951 | ||
| SD:mclust | 3 | 0.510 | 0.834 | 0.891 | ||
| SD:hclust | 4 | 0.404 | 0.626 | 0.741 | ||
| CV:hclust | 3 | 0.396 | 0.801 | 0.853 | ||
| SD:kmeans | 2 | 0.338 | 0.846 | 0.888 | ||
| MAD:hclust | 2 | 0.172 | 0.595 | 0.809 |
**: 1-PAC > 0.95, *: 1-PAC > 0.9
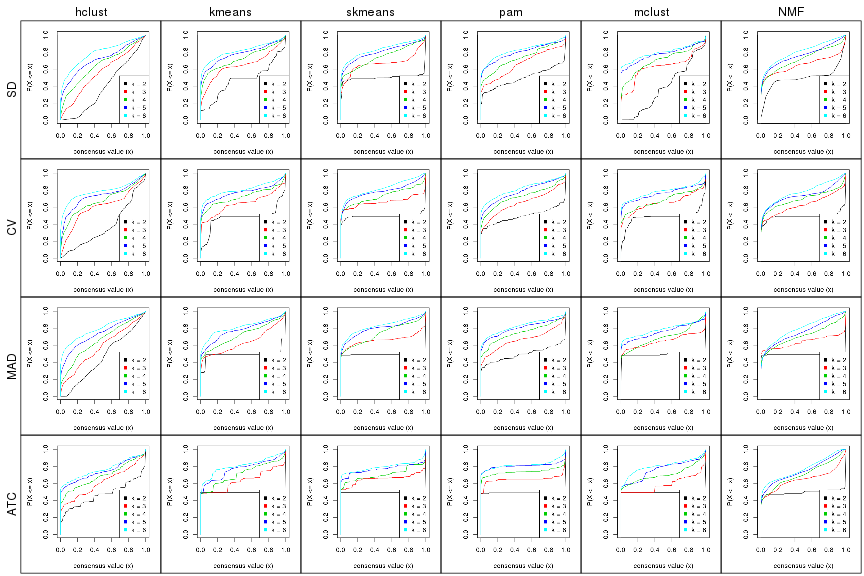
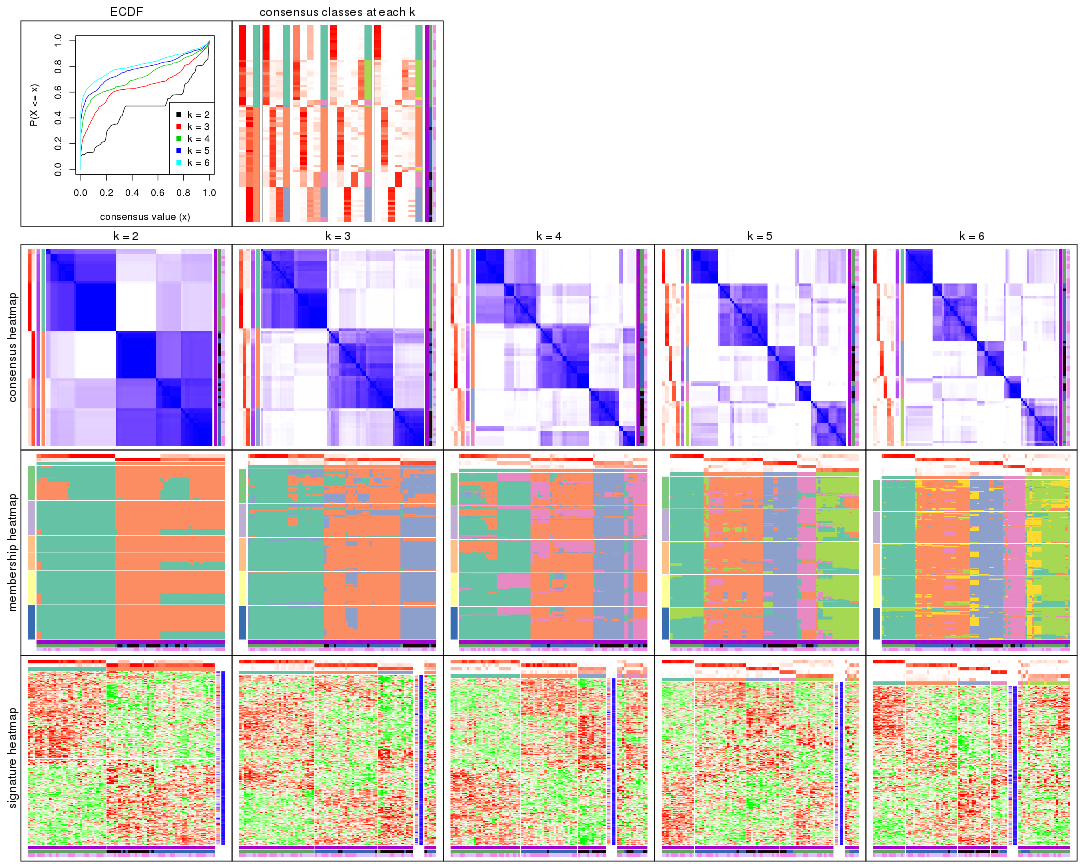
Cumulative distribution function curves of consensus matrix for all methods.
collect_plots(res_list, fun = plot_ecdf)
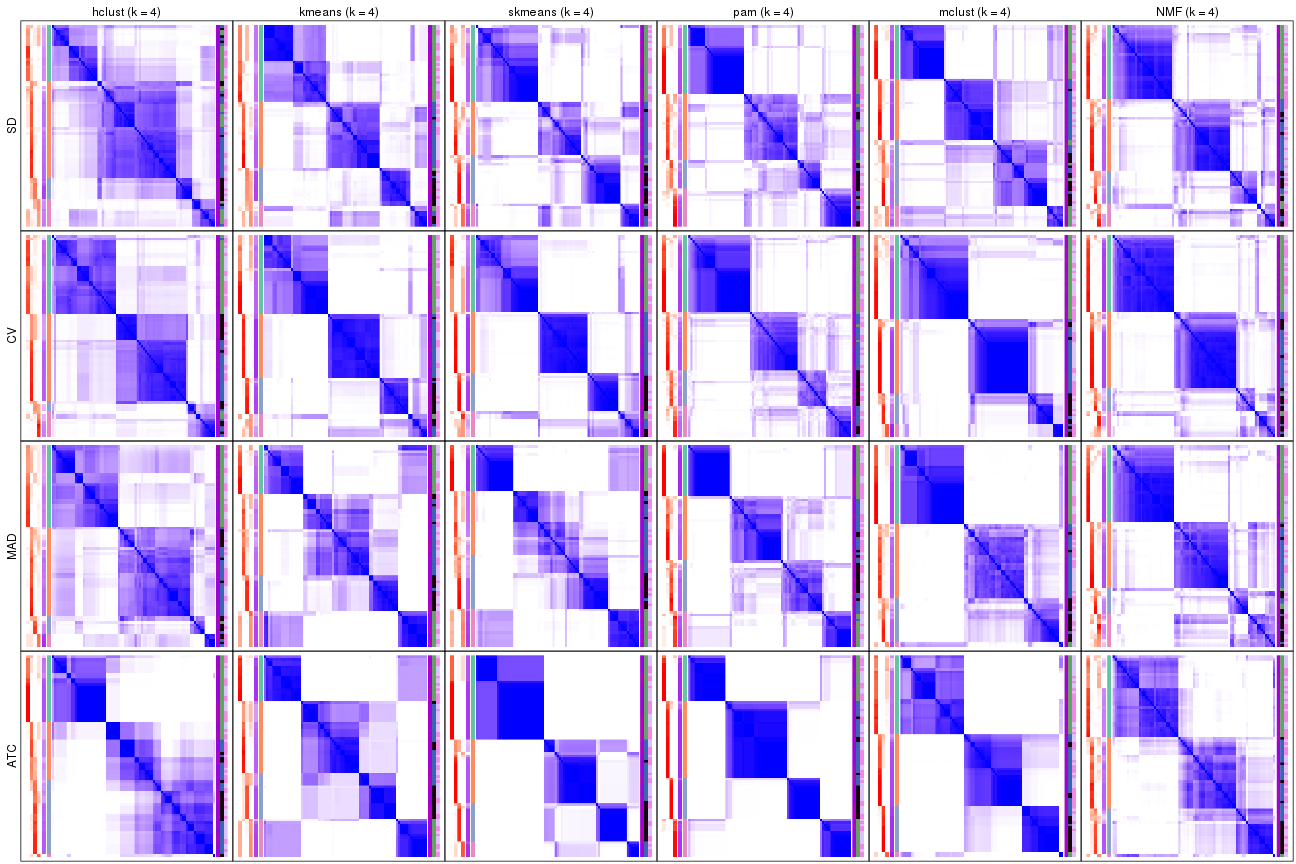
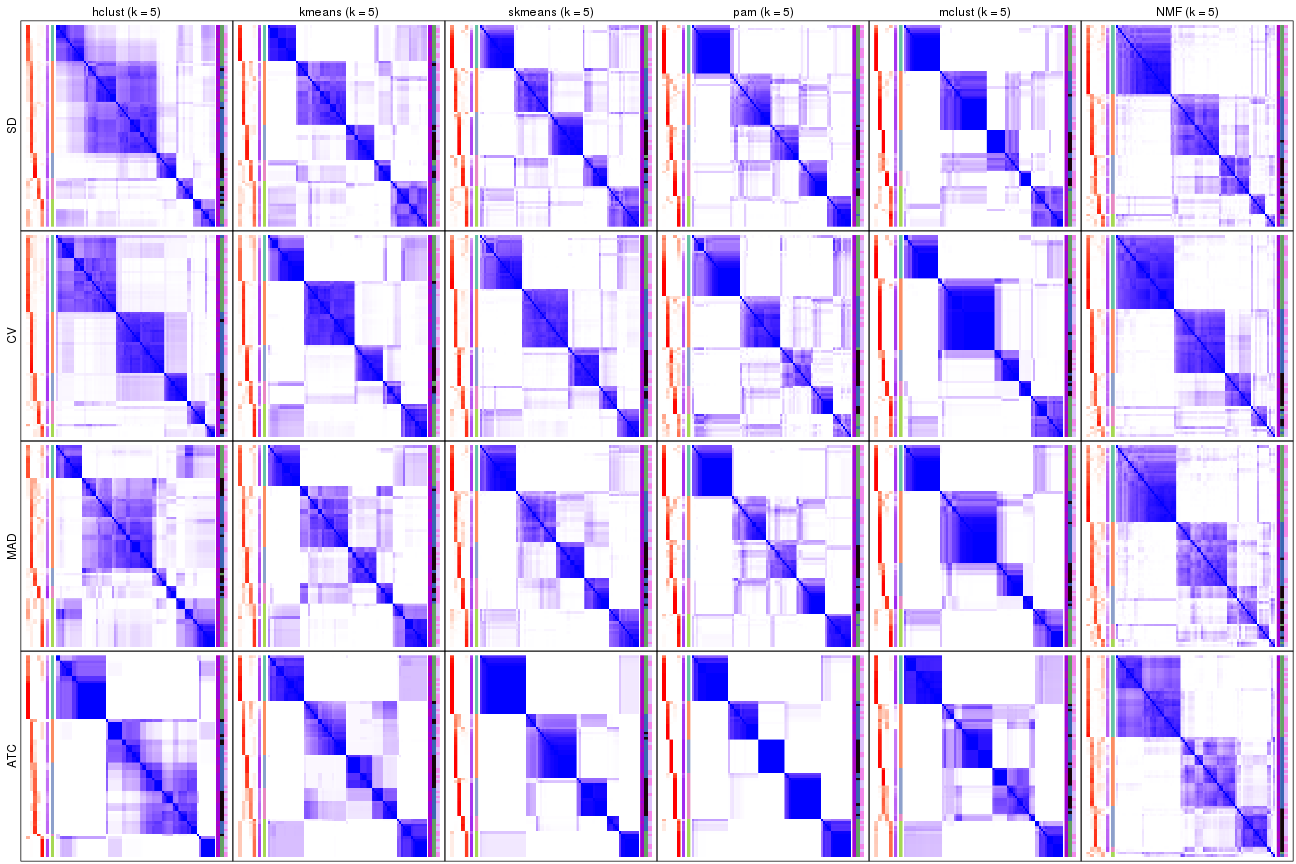
Consensus heatmaps for all methods. (What is a consensus heatmap?)
collect_plots(res_list, k = 2, fun = consensus_heatmap, mc.cores = 4)

collect_plots(res_list, k = 3, fun = consensus_heatmap, mc.cores = 4)

collect_plots(res_list, k = 4, fun = consensus_heatmap, mc.cores = 4)
collect_plots(res_list, k = 5, fun = consensus_heatmap, mc.cores = 4)
collect_plots(res_list, k = 6, fun = consensus_heatmap, mc.cores = 4)
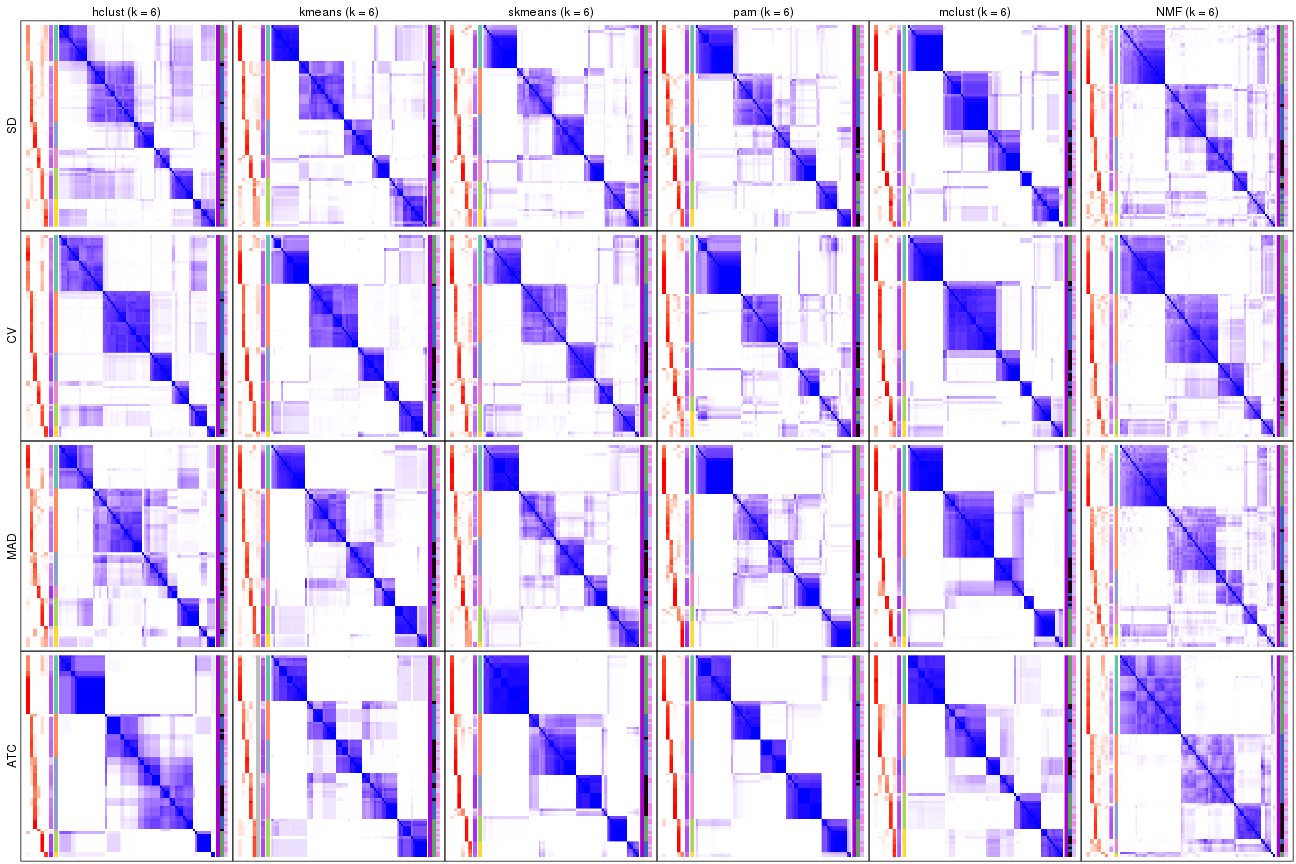
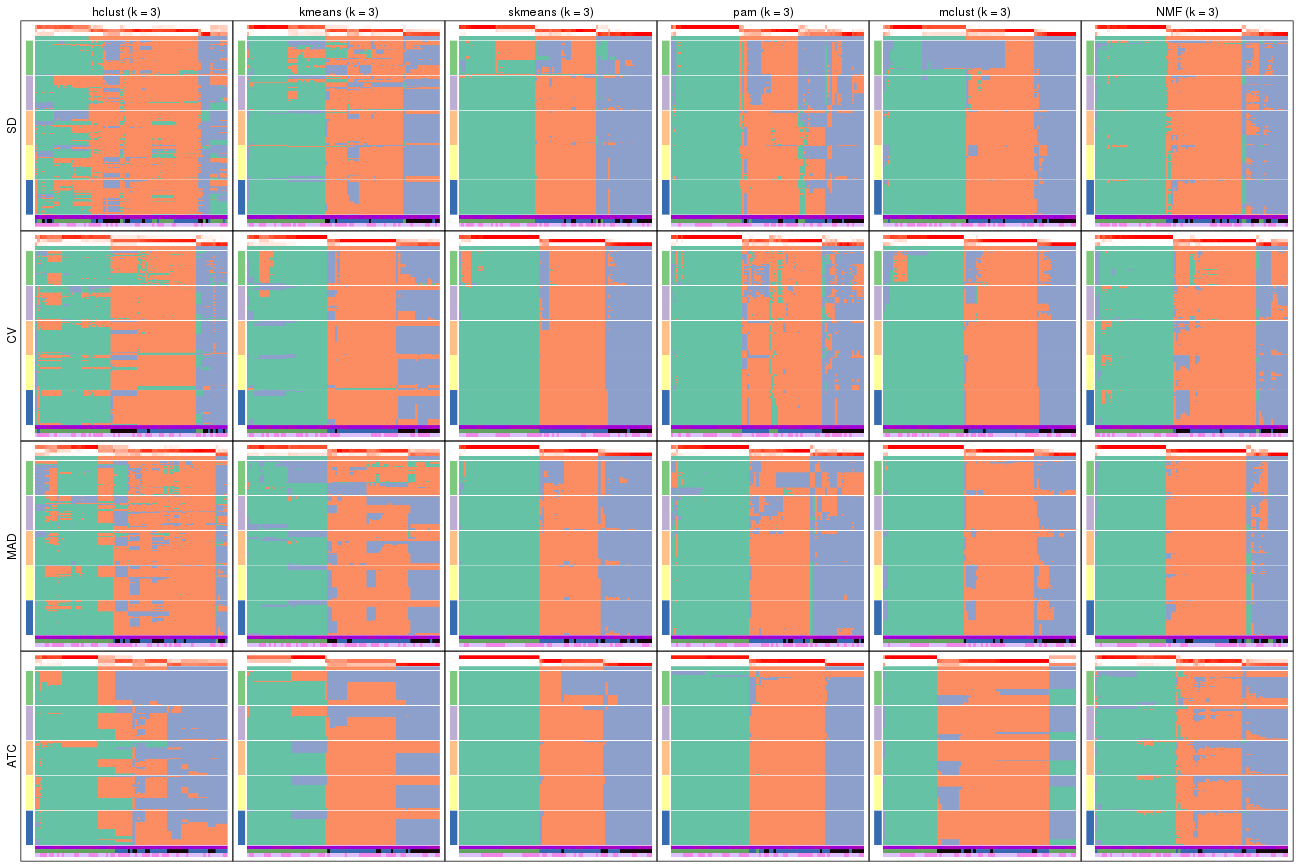
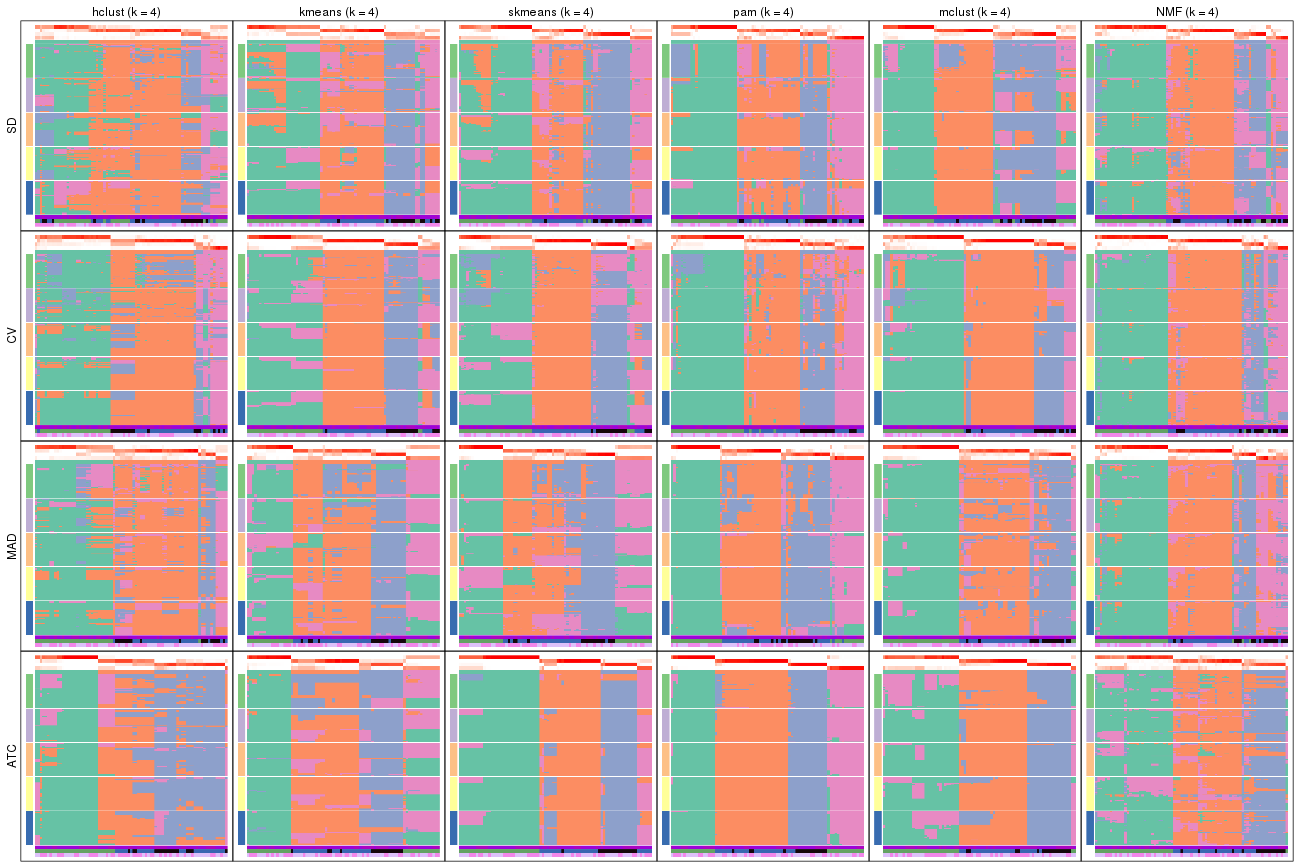
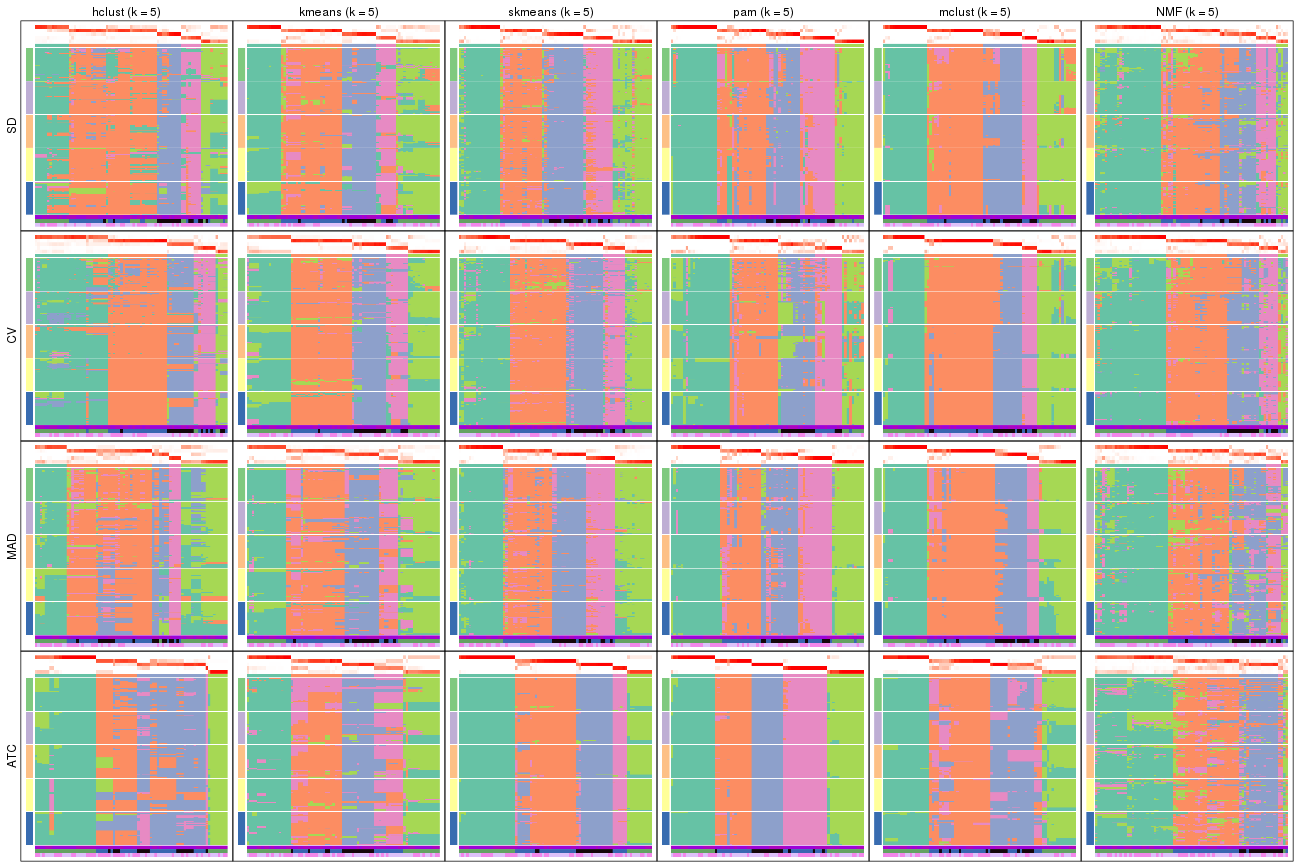
Membership heatmaps for all methods. (What is a membership heatmap?)
collect_plots(res_list, k = 2, fun = membership_heatmap, mc.cores = 4)

collect_plots(res_list, k = 3, fun = membership_heatmap, mc.cores = 4)
collect_plots(res_list, k = 4, fun = membership_heatmap, mc.cores = 4)
collect_plots(res_list, k = 5, fun = membership_heatmap, mc.cores = 4)
collect_plots(res_list, k = 6, fun = membership_heatmap, mc.cores = 4)

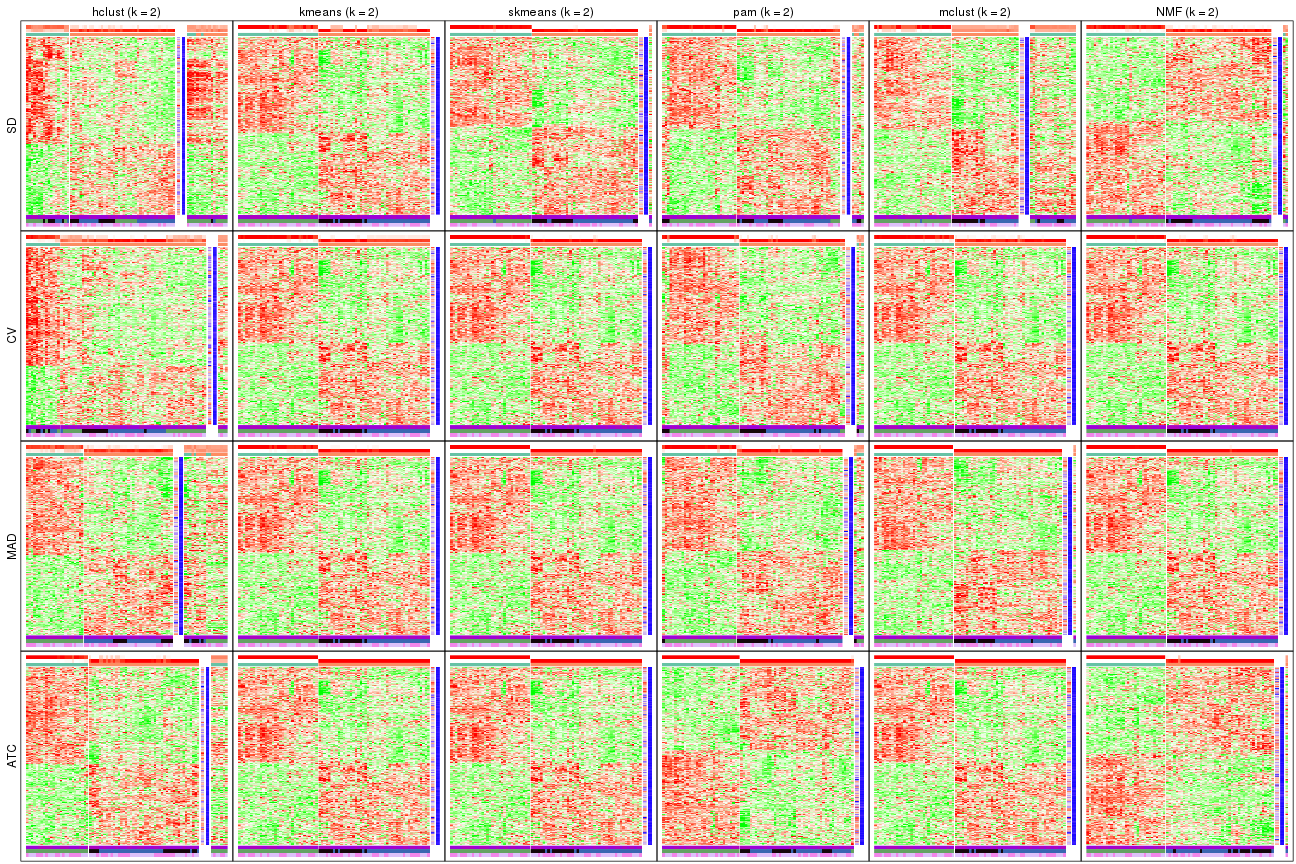
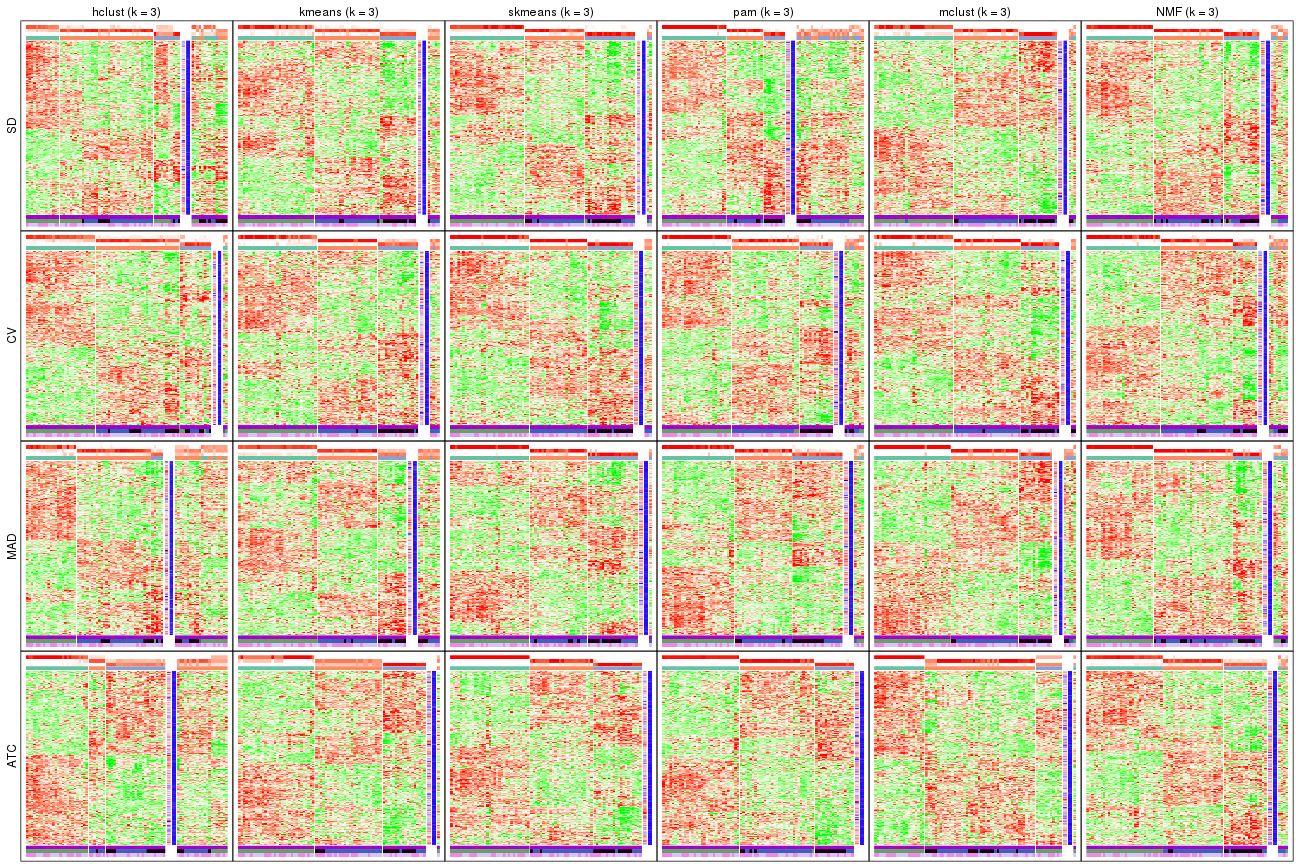
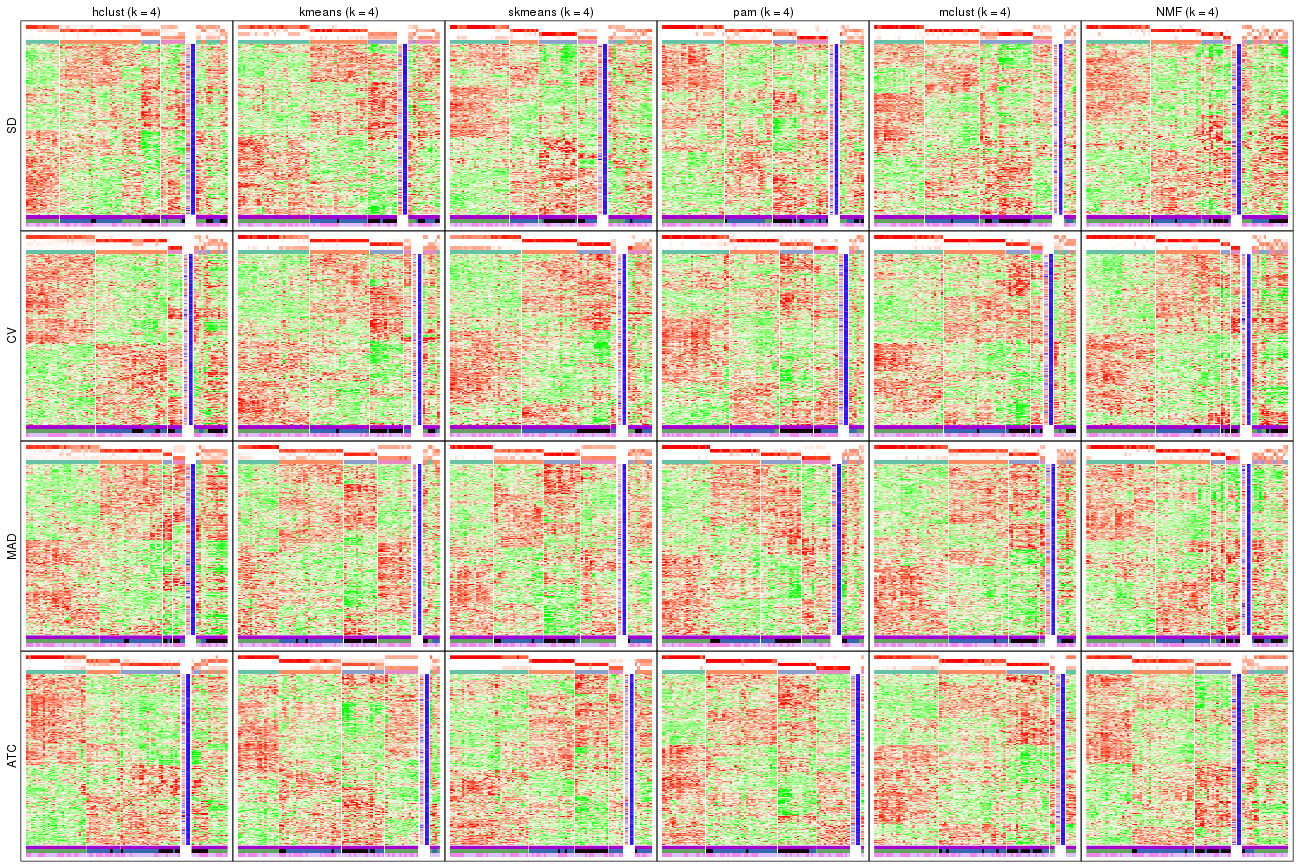
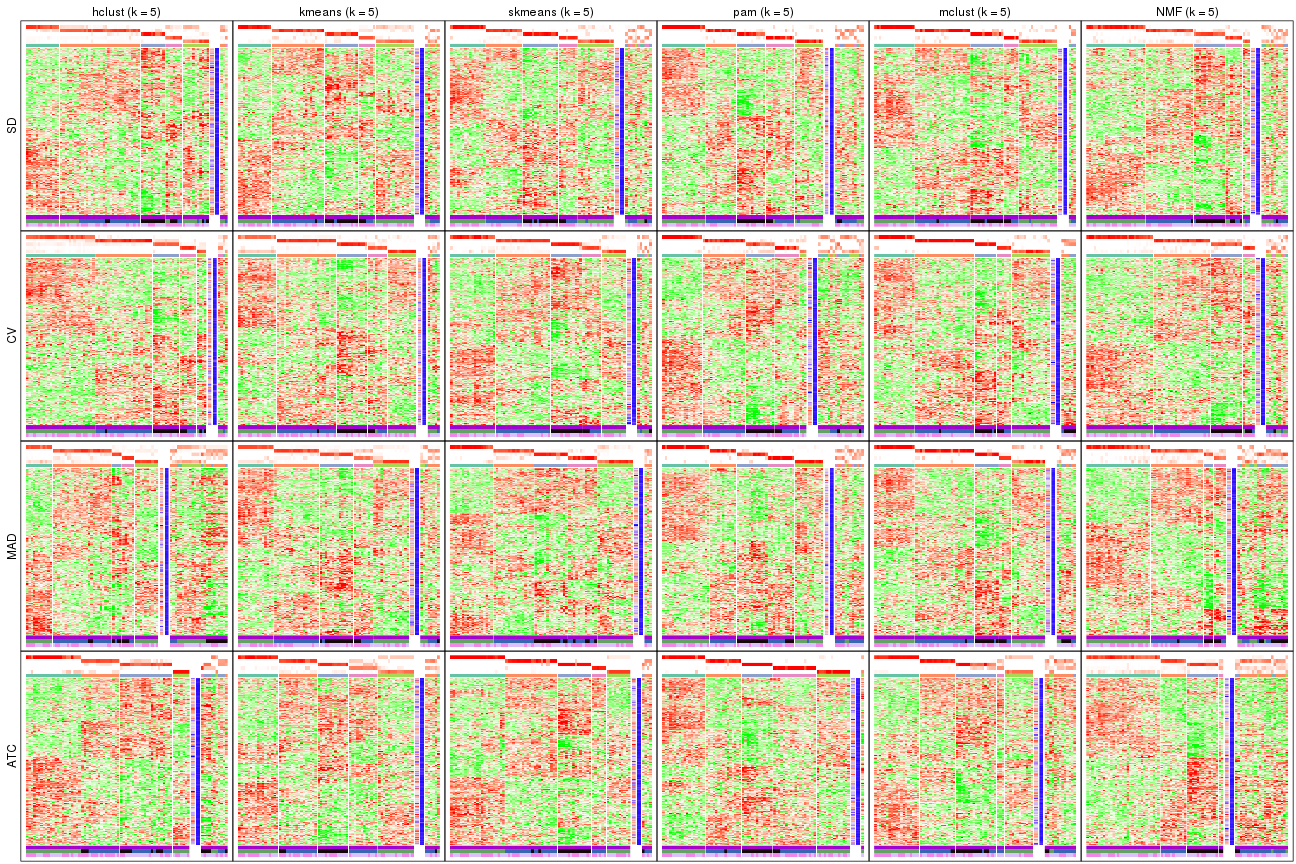
Signature heatmaps for all methods. (What is a signature heatmap?)
Note in following heatmaps, rows are scaled.
collect_plots(res_list, k = 2, fun = get_signatures, mc.cores = 4)
collect_plots(res_list, k = 3, fun = get_signatures, mc.cores = 4)
collect_plots(res_list, k = 4, fun = get_signatures, mc.cores = 4)
collect_plots(res_list, k = 5, fun = get_signatures, mc.cores = 4)
collect_plots(res_list, k = 6, fun = get_signatures, mc.cores = 4)
The statistics used for measuring the stability of consensus partitioning. (How are they defined?)
get_stats(res_list, k = 2)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> SD:NMF 2 0.773 0.909 0.948 0.498 0.503 0.503
#> CV:NMF 2 0.998 0.980 0.989 0.495 0.507 0.507
#> MAD:NMF 2 1.000 0.998 0.999 0.493 0.507 0.507
#> ATC:NMF 2 1.000 0.972 0.989 0.496 0.507 0.507
#> SD:skmeans 2 1.000 0.975 0.988 0.498 0.503 0.503
#> CV:skmeans 2 1.000 0.989 0.994 0.494 0.507 0.507
#> MAD:skmeans 2 1.000 0.997 0.999 0.494 0.507 0.507
#> ATC:skmeans 2 1.000 1.000 1.000 0.493 0.507 0.507
#> SD:mclust 2 0.176 0.377 0.652 0.380 0.537 0.537
#> CV:mclust 2 0.922 0.959 0.972 0.488 0.507 0.507
#> MAD:mclust 2 1.000 0.983 0.993 0.494 0.507 0.507
#> ATC:mclust 2 1.000 1.000 1.000 0.493 0.507 0.507
#> SD:kmeans 2 0.338 0.846 0.888 0.474 0.507 0.507
#> CV:kmeans 2 0.584 0.943 0.951 0.482 0.507 0.507
#> MAD:kmeans 2 1.000 0.979 0.986 0.492 0.507 0.507
#> ATC:kmeans 2 1.000 1.000 1.000 0.493 0.507 0.507
#> SD:pam 2 0.742 0.869 0.945 0.497 0.503 0.503
#> CV:pam 2 0.845 0.909 0.962 0.496 0.503 0.503
#> MAD:pam 2 0.849 0.909 0.962 0.496 0.503 0.503
#> ATC:pam 2 1.000 0.998 0.999 0.489 0.512 0.512
#> SD:hclust 2 0.197 0.548 0.770 0.388 0.582 0.582
#> CV:hclust 2 0.257 0.749 0.836 0.375 0.705 0.705
#> MAD:hclust 2 0.172 0.595 0.809 0.457 0.523 0.523
#> ATC:hclust 2 0.608 0.851 0.930 0.472 0.507 0.507
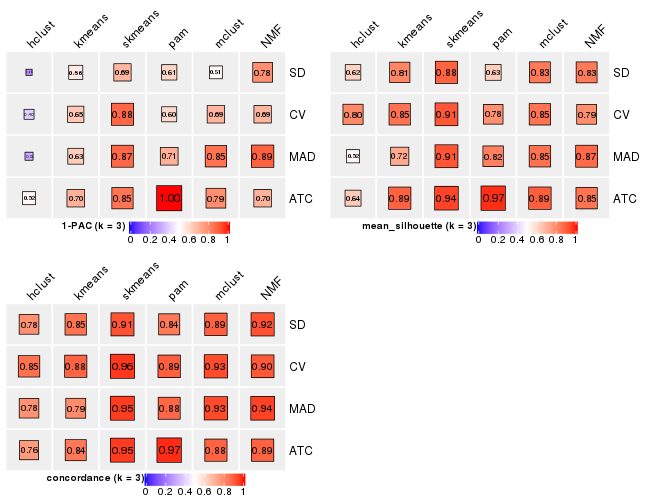
get_stats(res_list, k = 3)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> SD:NMF 3 0.785 0.832 0.921 0.309 0.776 0.580
#> CV:NMF 3 0.692 0.789 0.904 0.274 0.853 0.713
#> MAD:NMF 3 0.889 0.873 0.945 0.294 0.806 0.630
#> ATC:NMF 3 0.698 0.849 0.885 0.304 0.796 0.612
#> SD:skmeans 3 0.688 0.883 0.915 0.341 0.788 0.595
#> CV:skmeans 3 0.878 0.907 0.959 0.341 0.833 0.672
#> MAD:skmeans 3 0.875 0.912 0.953 0.343 0.829 0.662
#> ATC:skmeans 3 0.847 0.942 0.954 0.325 0.831 0.667
#> SD:mclust 3 0.510 0.834 0.891 0.646 0.666 0.453
#> CV:mclust 3 0.693 0.851 0.928 0.333 0.844 0.693
#> MAD:mclust 3 0.850 0.853 0.931 0.316 0.840 0.685
#> ATC:mclust 3 0.786 0.893 0.884 0.193 0.921 0.845
#> SD:kmeans 3 0.559 0.808 0.852 0.370 0.840 0.687
#> CV:kmeans 3 0.647 0.852 0.884 0.336 0.836 0.678
#> MAD:kmeans 3 0.631 0.722 0.792 0.295 0.861 0.726
#> ATC:kmeans 3 0.699 0.887 0.837 0.284 0.817 0.646
#> SD:pam 3 0.610 0.631 0.839 0.333 0.707 0.477
#> CV:pam 3 0.600 0.782 0.893 0.313 0.789 0.603
#> MAD:pam 3 0.706 0.818 0.876 0.342 0.804 0.620
#> ATC:pam 3 1.000 0.969 0.974 0.327 0.839 0.685
#> SD:hclust 3 0.246 0.617 0.783 0.448 0.751 0.601
#> CV:hclust 3 0.396 0.801 0.853 0.614 0.645 0.503
#> MAD:hclust 3 0.321 0.523 0.779 0.268 0.936 0.879
#> ATC:hclust 3 0.519 0.635 0.759 0.301 0.723 0.501
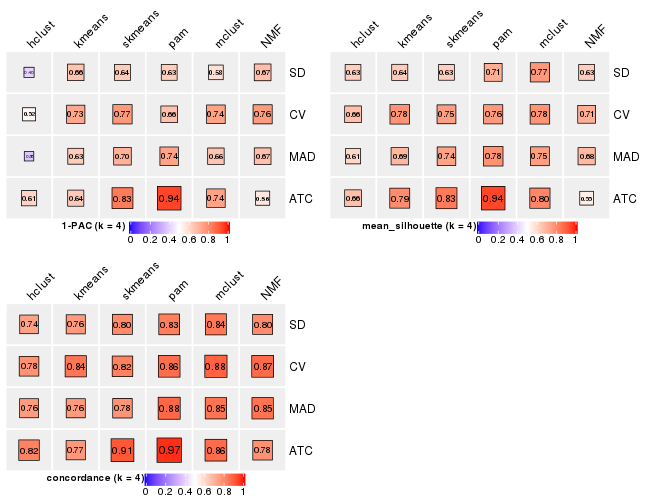
get_stats(res_list, k = 4)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> SD:NMF 4 0.666 0.631 0.795 0.1047 0.857 0.629
#> CV:NMF 4 0.761 0.709 0.868 0.1065 0.917 0.781
#> MAD:NMF 4 0.665 0.684 0.851 0.1145 0.855 0.627
#> ATC:NMF 4 0.563 0.547 0.781 0.0933 0.907 0.759
#> SD:skmeans 4 0.636 0.627 0.797 0.1127 0.897 0.709
#> CV:skmeans 4 0.768 0.749 0.816 0.1066 0.917 0.765
#> MAD:skmeans 4 0.700 0.740 0.776 0.1161 0.898 0.703
#> ATC:skmeans 4 0.831 0.834 0.906 0.0809 0.904 0.742
#> SD:mclust 4 0.583 0.766 0.839 0.1286 0.796 0.506
#> CV:mclust 4 0.741 0.778 0.885 0.0507 0.954 0.874
#> MAD:mclust 4 0.655 0.750 0.849 0.0674 0.951 0.865
#> ATC:mclust 4 0.739 0.805 0.865 0.2000 0.752 0.504
#> SD:kmeans 4 0.657 0.639 0.760 0.1209 0.912 0.760
#> CV:kmeans 4 0.727 0.778 0.844 0.1251 0.929 0.798
#> MAD:kmeans 4 0.633 0.690 0.759 0.1367 0.872 0.668
#> ATC:kmeans 4 0.641 0.794 0.766 0.1269 0.905 0.725
#> SD:pam 4 0.630 0.711 0.826 0.1076 0.799 0.497
#> CV:pam 4 0.663 0.762 0.862 0.1144 0.891 0.701
#> MAD:pam 4 0.738 0.780 0.876 0.1252 0.868 0.630
#> ATC:pam 4 0.940 0.937 0.969 0.1359 0.904 0.730
#> SD:hclust 4 0.404 0.626 0.741 0.1582 0.908 0.781
#> CV:hclust 4 0.522 0.664 0.780 0.1131 0.978 0.941
#> MAD:hclust 4 0.377 0.605 0.757 0.1409 0.782 0.587
#> ATC:hclust 4 0.609 0.665 0.816 0.1254 0.929 0.801
get_stats(res_list, k = 5)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> SD:NMF 5 0.659 0.675 0.824 0.0592 0.894 0.671
#> CV:NMF 5 0.694 0.751 0.858 0.0612 0.921 0.758
#> MAD:NMF 5 0.619 0.608 0.758 0.0634 0.930 0.778
#> ATC:NMF 5 0.617 0.548 0.753 0.0571 0.883 0.693
#> SD:skmeans 5 0.741 0.717 0.862 0.0779 0.872 0.572
#> CV:skmeans 5 0.777 0.790 0.874 0.0756 0.905 0.676
#> MAD:skmeans 5 0.762 0.811 0.879 0.0829 0.888 0.598
#> ATC:skmeans 5 0.916 0.890 0.937 0.0896 0.925 0.757
#> SD:mclust 5 0.753 0.803 0.901 0.0968 0.845 0.517
#> CV:mclust 5 0.831 0.808 0.908 0.1121 0.876 0.638
#> MAD:mclust 5 0.795 0.786 0.897 0.0950 0.853 0.586
#> ATC:mclust 5 0.729 0.676 0.818 0.0809 0.894 0.680
#> SD:kmeans 5 0.681 0.773 0.831 0.0742 0.892 0.645
#> CV:kmeans 5 0.766 0.802 0.845 0.0674 0.924 0.738
#> MAD:kmeans 5 0.677 0.703 0.794 0.0763 0.918 0.710
#> ATC:kmeans 5 0.708 0.776 0.780 0.0807 0.920 0.700
#> SD:pam 5 0.761 0.730 0.880 0.0878 0.855 0.527
#> CV:pam 5 0.685 0.615 0.796 0.0784 0.906 0.678
#> MAD:pam 5 0.794 0.743 0.885 0.0716 0.876 0.565
#> ATC:pam 5 0.950 0.941 0.972 0.0927 0.906 0.657
#> SD:hclust 5 0.499 0.717 0.800 0.1018 0.935 0.806
#> CV:hclust 5 0.614 0.790 0.835 0.0877 0.903 0.727
#> MAD:hclust 5 0.539 0.530 0.733 0.1202 0.920 0.780
#> ATC:hclust 5 0.678 0.690 0.808 0.0759 0.939 0.813
get_stats(res_list, k = 6)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> SD:NMF 6 0.657 0.590 0.768 0.0551 0.915 0.683
#> CV:NMF 6 0.666 0.663 0.799 0.0565 0.935 0.771
#> MAD:NMF 6 0.615 0.515 0.743 0.0527 0.938 0.780
#> ATC:NMF 6 0.620 0.458 0.737 0.0333 0.945 0.835
#> SD:skmeans 6 0.763 0.669 0.817 0.0377 0.951 0.765
#> CV:skmeans 6 0.757 0.651 0.806 0.0437 0.980 0.909
#> MAD:skmeans 6 0.738 0.574 0.770 0.0364 0.971 0.858
#> ATC:skmeans 6 0.878 0.823 0.909 0.0325 0.983 0.928
#> SD:mclust 6 0.765 0.764 0.871 0.0289 0.991 0.958
#> CV:mclust 6 0.818 0.792 0.888 0.0332 0.960 0.835
#> MAD:mclust 6 0.827 0.781 0.892 0.0353 0.960 0.837
#> ATC:mclust 6 0.819 0.832 0.826 0.0554 0.944 0.763
#> SD:kmeans 6 0.746 0.606 0.791 0.0441 0.976 0.891
#> CV:kmeans 6 0.776 0.754 0.843 0.0467 0.972 0.876
#> MAD:kmeans 6 0.748 0.756 0.820 0.0471 0.944 0.748
#> ATC:kmeans 6 0.703 0.757 0.806 0.0504 0.971 0.861
#> SD:pam 6 0.766 0.722 0.827 0.0307 0.972 0.862
#> CV:pam 6 0.737 0.585 0.803 0.0432 0.945 0.760
#> MAD:pam 6 0.778 0.687 0.829 0.0311 0.951 0.767
#> ATC:pam 6 0.898 0.876 0.926 0.0178 0.992 0.956
#> SD:hclust 6 0.607 0.687 0.739 0.1043 0.907 0.661
#> CV:hclust 6 0.727 0.787 0.841 0.0755 0.931 0.743
#> MAD:hclust 6 0.653 0.586 0.762 0.0766 0.849 0.523
#> ATC:hclust 6 0.702 0.692 0.805 0.0315 0.985 0.945
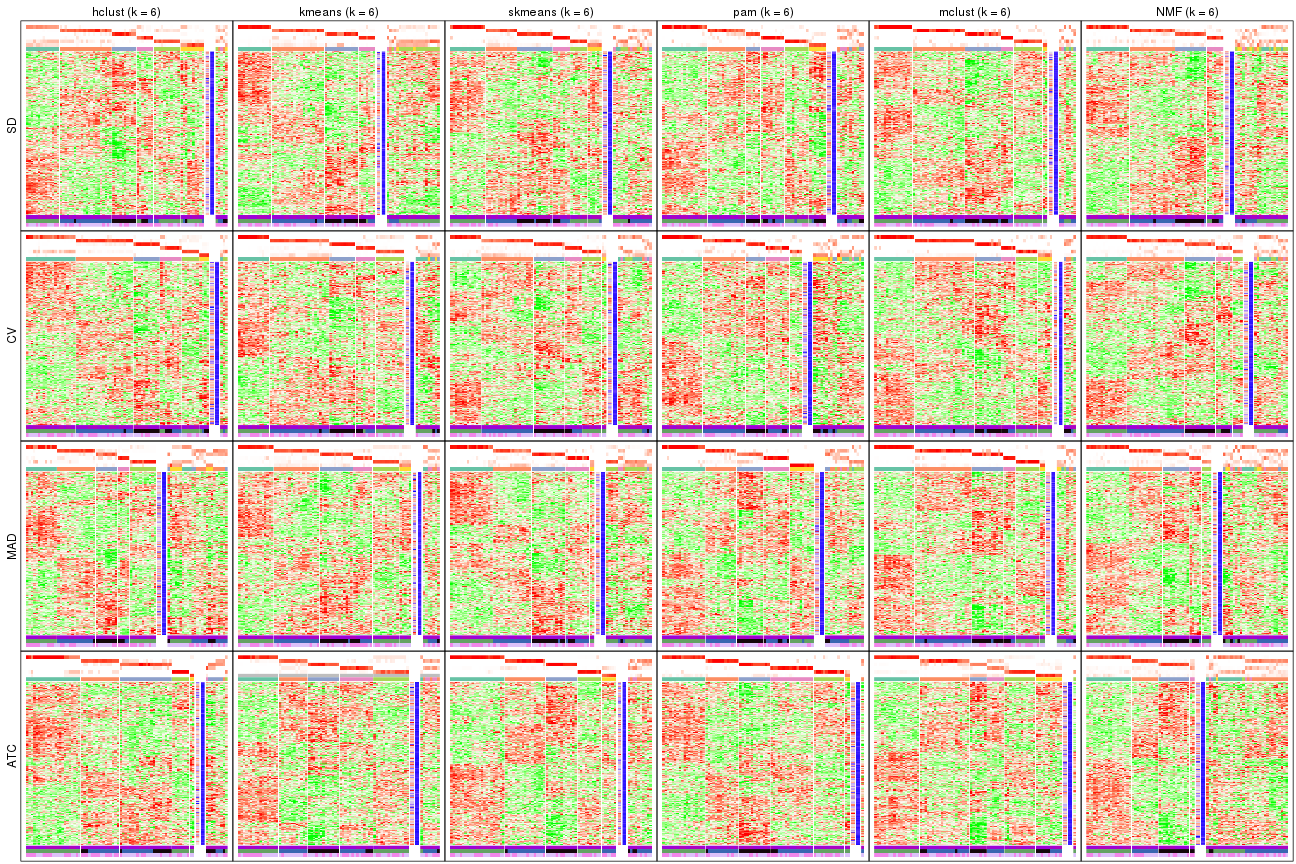
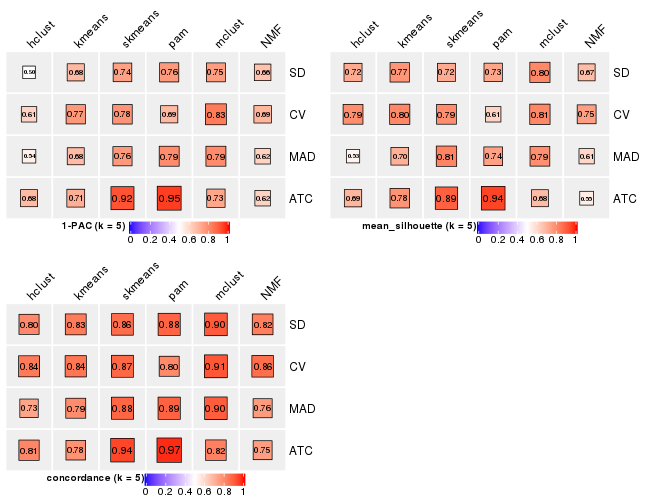
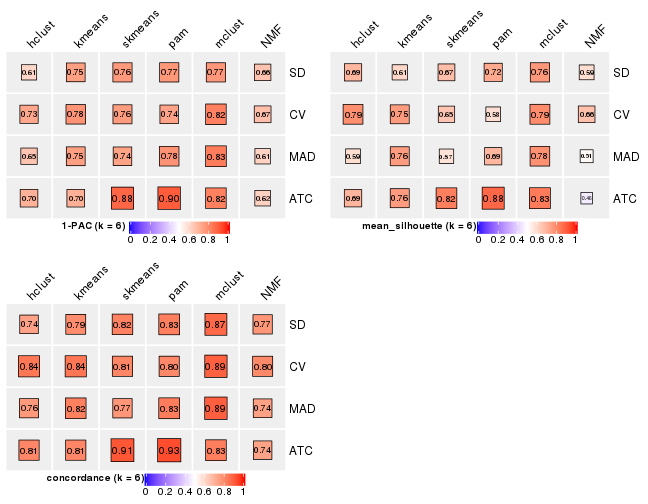
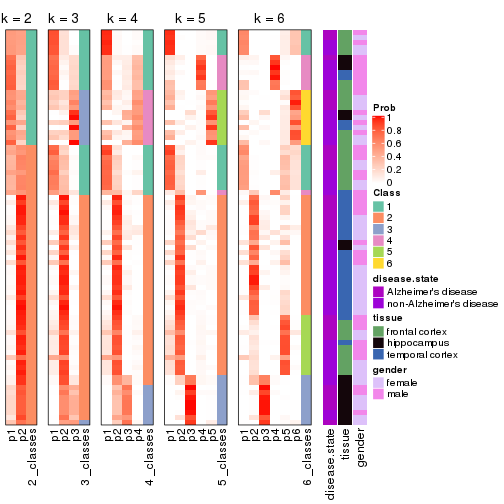
Following heatmap plots the partition for each combination of methods and the lightness correspond to the silhouette scores for samples in each method. On top the consensus subgroup is inferred from all methods by taking the mean silhouette scores as weight.
collect_stats(res_list, k = 2)
collect_stats(res_list, k = 3)
collect_stats(res_list, k = 4)
collect_stats(res_list, k = 5)
collect_stats(res_list, k = 6)
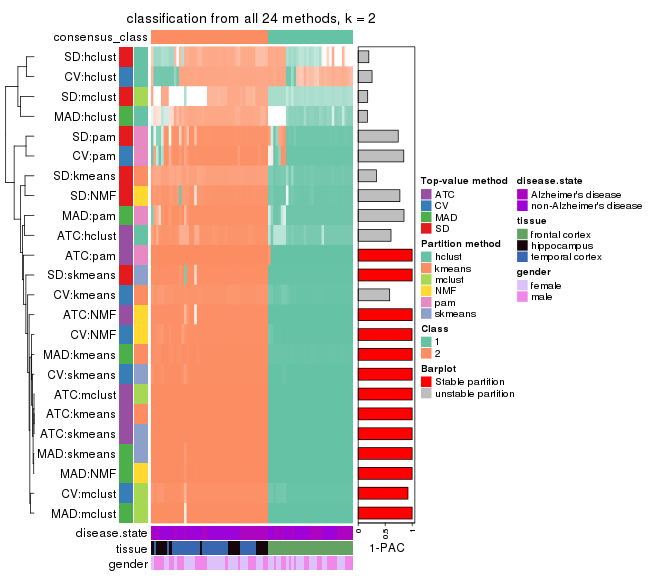
Collect partitions from all methods:
collect_classes(res_list, k = 2)
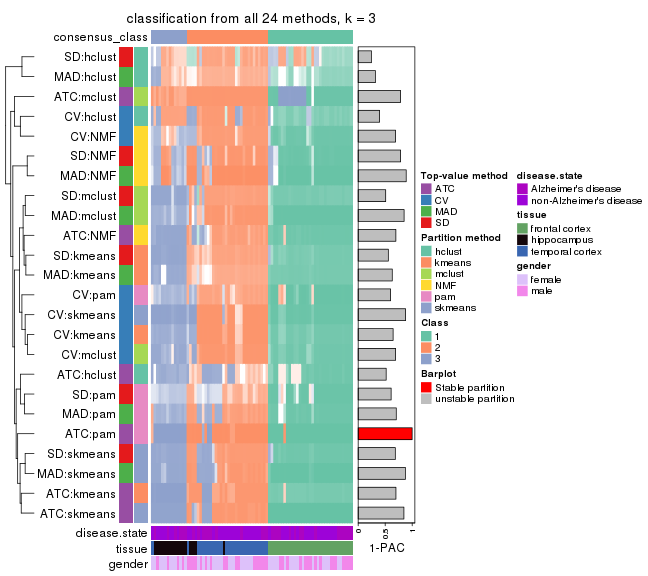
collect_classes(res_list, k = 3)
collect_classes(res_list, k = 4)
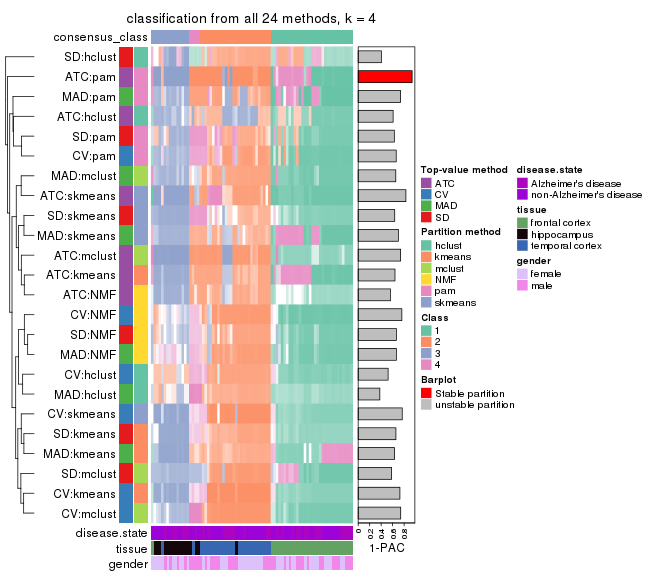
collect_classes(res_list, k = 5)
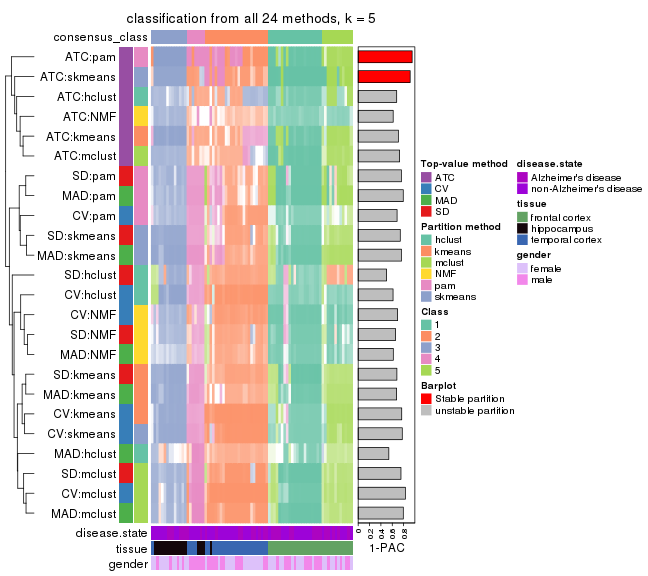
collect_classes(res_list, k = 6)
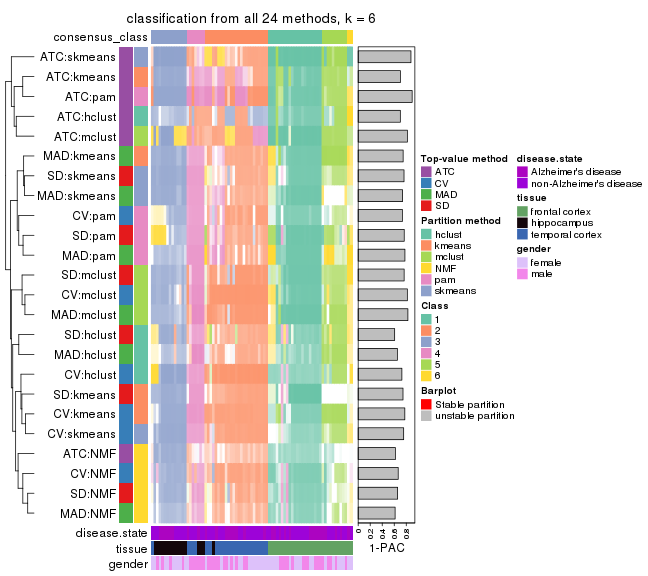
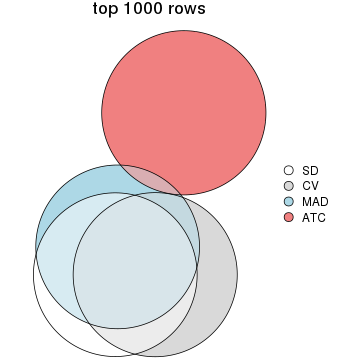
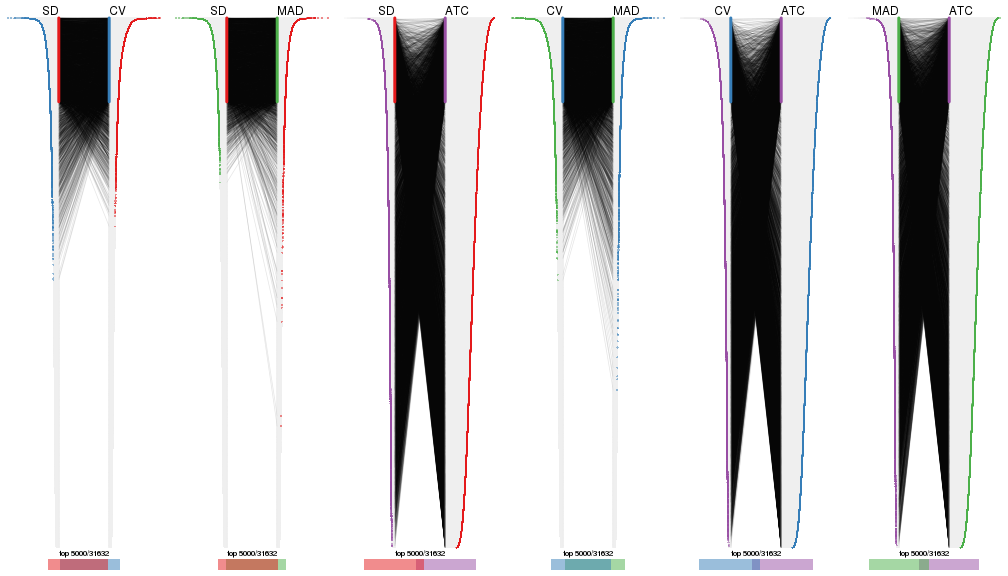
Overlap of top rows from different top-row methods:
top_rows_overlap(res_list, top_n = 1000, method = "euler")
top_rows_overlap(res_list, top_n = 2000, method = "euler")
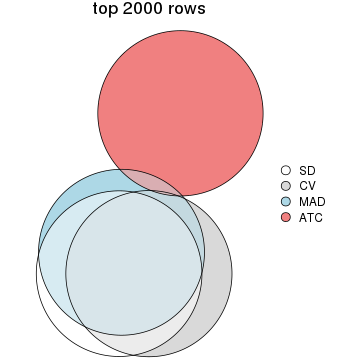
top_rows_overlap(res_list, top_n = 3000, method = "euler")
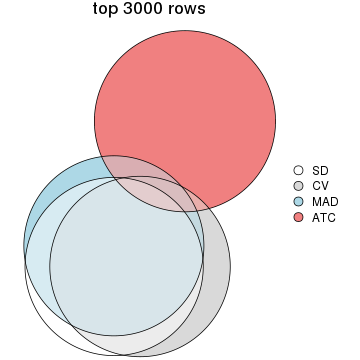
top_rows_overlap(res_list, top_n = 4000, method = "euler")
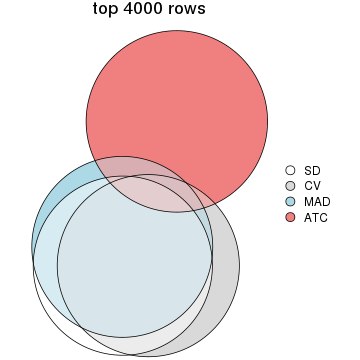
top_rows_overlap(res_list, top_n = 5000, method = "euler")
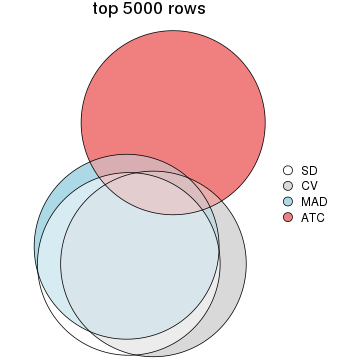
Also visualize the correspondance of rankings between different top-row methods:
top_rows_overlap(res_list, top_n = 1000, method = "correspondance")
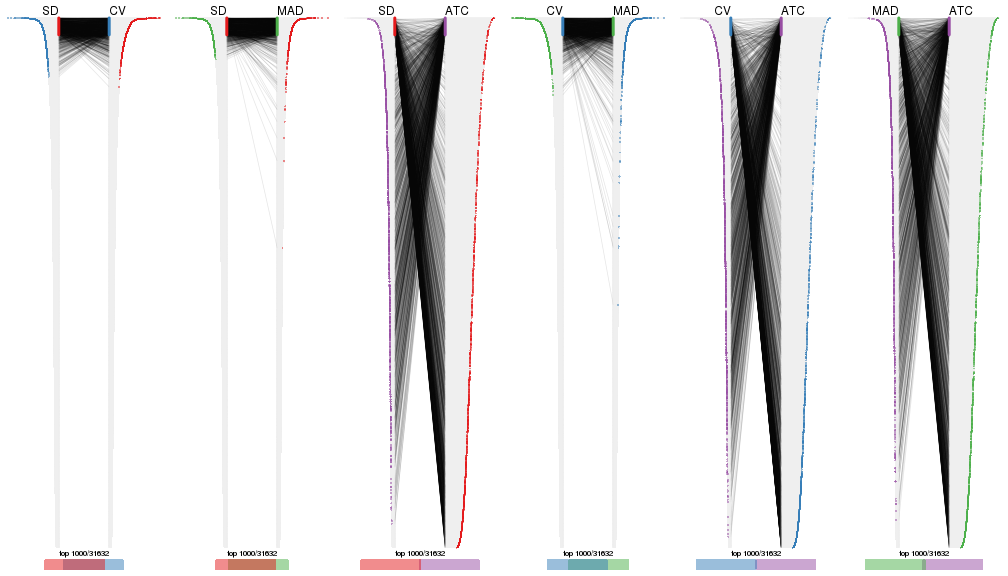
top_rows_overlap(res_list, top_n = 2000, method = "correspondance")
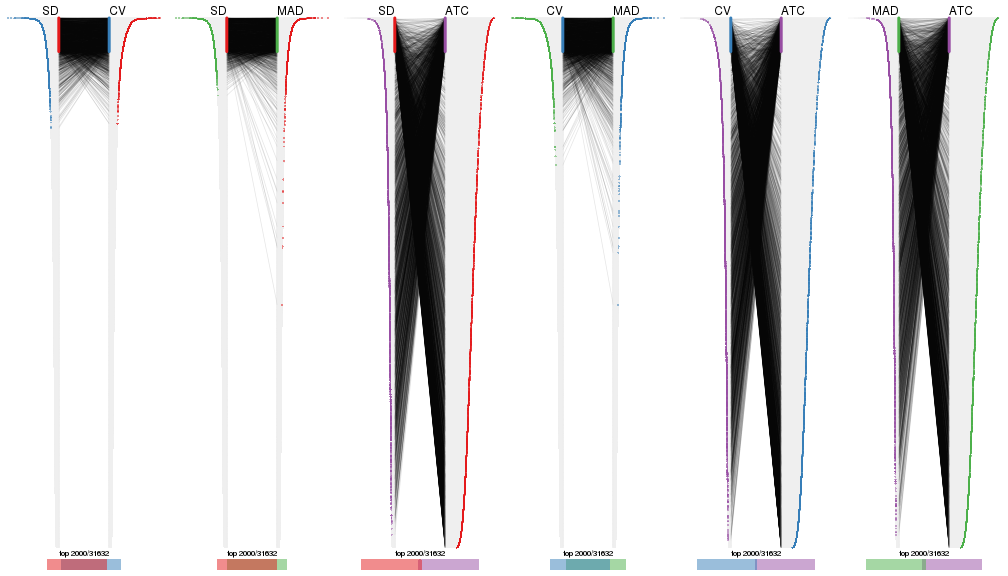
top_rows_overlap(res_list, top_n = 3000, method = "correspondance")
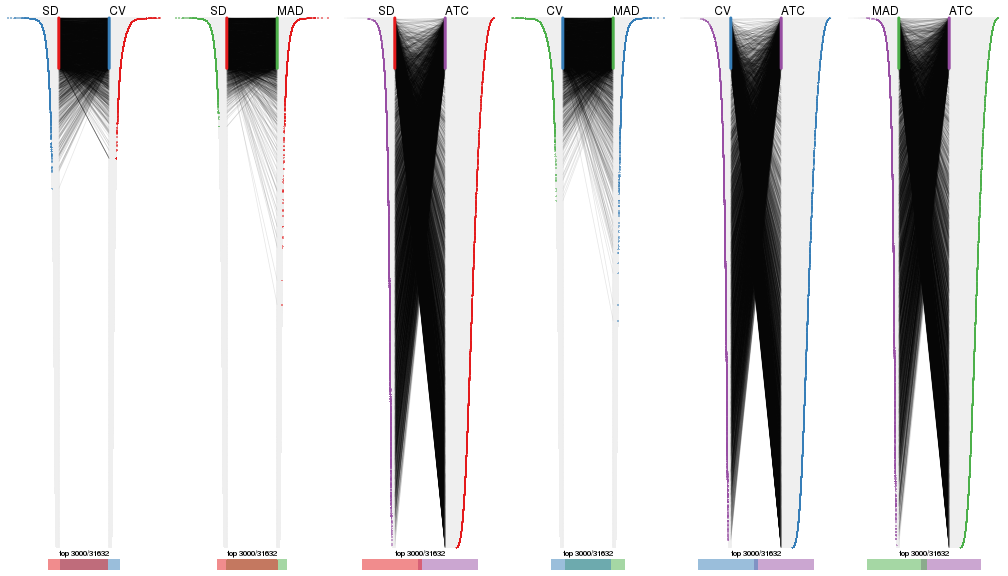
top_rows_overlap(res_list, top_n = 4000, method = "correspondance")
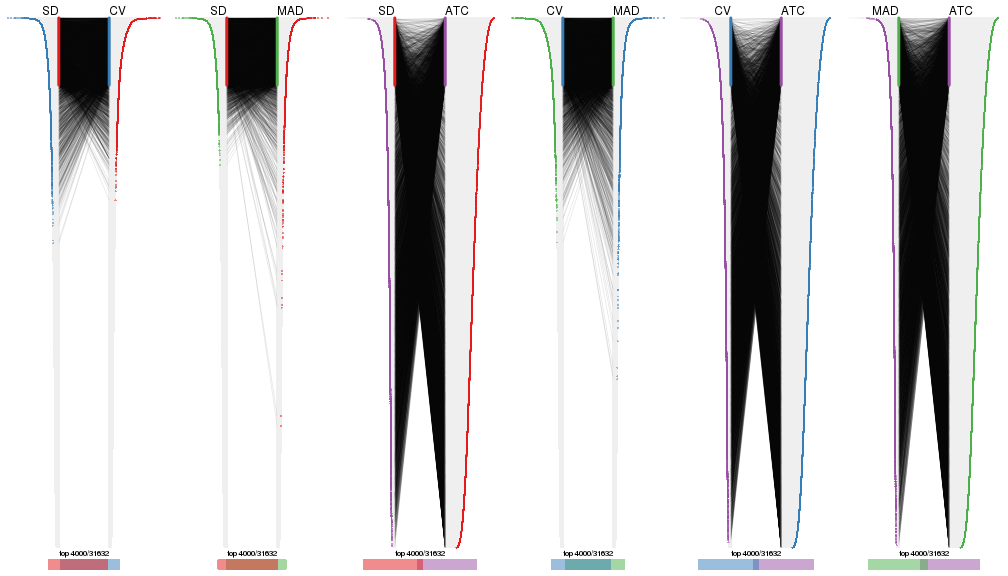
top_rows_overlap(res_list, top_n = 5000, method = "correspondance")
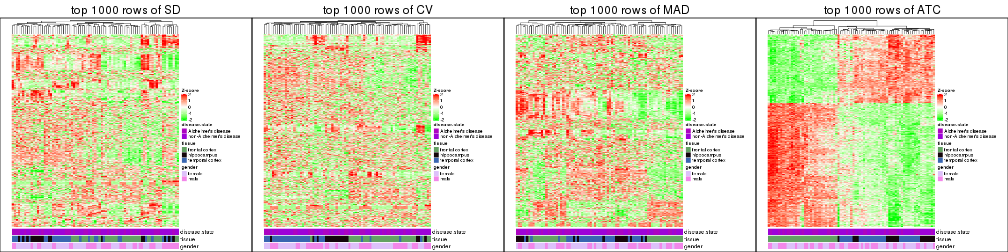
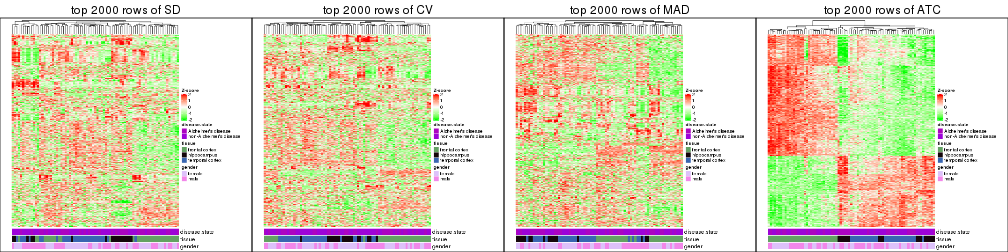
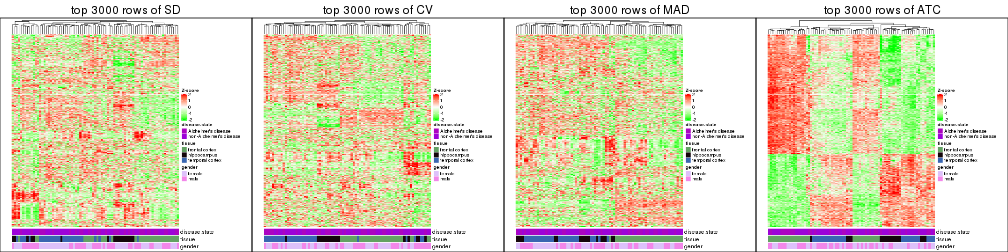
Heatmaps of the top rows:
top_rows_heatmap(res_list, top_n = 1000)
top_rows_heatmap(res_list, top_n = 2000)
top_rows_heatmap(res_list, top_n = 3000)
top_rows_heatmap(res_list, top_n = 4000)
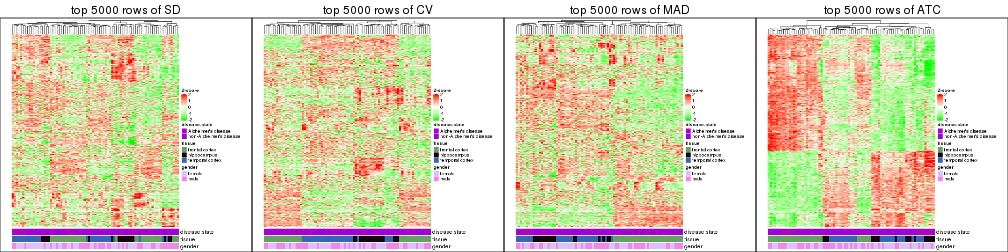
top_rows_heatmap(res_list, top_n = 5000)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res_list, k = 2)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 77 0.714 1.36e-16 0.621 2
#> CV:NMF 79 0.599 7.00e-18 0.984 2
#> MAD:NMF 79 0.599 7.00e-18 0.984 2
#> ATC:NMF 78 0.654 1.15e-17 0.901 2
#> SD:skmeans 78 0.471 8.21e-17 1.000 2
#> CV:skmeans 79 0.599 7.00e-18 0.984 2
#> MAD:skmeans 79 0.599 7.00e-18 0.984 2
#> ATC:skmeans 79 0.599 7.00e-18 0.984 2
#> SD:mclust 60 0.959 6.15e-13 0.154 2
#> CV:mclust 79 0.599 7.00e-18 0.984 2
#> MAD:mclust 78 0.517 1.15e-17 1.000 2
#> ATC:mclust 79 0.599 7.00e-18 0.984 2
#> SD:kmeans 79 0.599 7.00e-18 0.984 2
#> CV:kmeans 79 0.599 7.00e-18 0.984 2
#> MAD:kmeans 79 0.599 7.00e-18 0.984 2
#> ATC:kmeans 79 0.599 7.00e-18 0.984 2
#> SD:pam 74 0.319 1.56e-11 0.427 2
#> CV:pam 76 0.494 2.16e-13 0.874 2
#> MAD:pam 75 0.422 3.58e-16 1.000 2
#> ATC:pam 79 0.473 5.24e-17 0.814 2
#> SD:hclust 62 0.399 3.28e-02 0.183 2
#> CV:hclust 75 0.204 4.10e-01 0.291 2
#> MAD:hclust 61 0.886 5.68e-14 0.644 2
#> ATC:hclust 72 0.607 2.32e-16 0.913 2
test_to_known_factors(res_list, k = 3)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 72 0.1083 2.07e-15 0.4898 3
#> CV:NMF 71 0.4269 3.73e-22 0.5256 3
#> MAD:NMF 73 0.2151 9.19e-16 0.3826 3
#> ATC:NMF 75 0.1800 1.21e-24 0.6669 3
#> SD:skmeans 77 0.1141 4.99e-19 0.2708 3
#> CV:skmeans 76 0.7682 5.18e-29 0.8704 3
#> MAD:skmeans 78 0.0661 1.20e-19 0.2426 3
#> ATC:skmeans 79 0.0687 2.64e-24 0.7726 3
#> SD:mclust 76 0.3231 9.33e-24 0.6508 3
#> CV:mclust 77 0.7292 9.52e-28 0.9518 3
#> MAD:mclust 74 0.5008 2.05e-26 0.6283 3
#> ATC:mclust 78 0.6766 4.62e-16 0.8685 3
#> SD:kmeans 74 0.2504 6.55e-24 0.1833 3
#> CV:kmeans 75 0.7693 2.12e-28 0.8743 3
#> MAD:kmeans 70 0.0832 2.21e-24 0.5546 3
#> ATC:kmeans 78 0.0823 9.50e-22 0.3785 3
#> SD:pam 51 0.4395 3.49e-15 0.0482 3
#> CV:pam 71 0.7895 1.04e-27 0.7989 3
#> MAD:pam 75 0.0617 7.14e-19 0.2451 3
#> ATC:pam 79 0.0836 6.92e-23 0.3727 3
#> SD:hclust 64 0.7158 1.69e-05 0.7158 3
#> CV:hclust 77 0.1214 4.38e-14 0.1378 3
#> MAD:hclust 57 0.5314 2.88e-12 0.2970 3
#> ATC:hclust 58 0.6917 7.96e-13 0.0773 3
test_to_known_factors(res_list, k = 4)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 60 0.1873 4.95e-14 0.12025 4
#> CV:NMF 64 0.3132 7.46e-17 0.12536 4
#> MAD:NMF 64 0.5146 1.02e-17 0.10992 4
#> ATC:NMF 60 0.0814 3.01e-19 0.14721 4
#> SD:skmeans 61 0.3316 1.33e-17 0.02686 4
#> CV:skmeans 69 0.5247 2.65e-27 0.35545 4
#> MAD:skmeans 69 0.1449 3.99e-18 0.11559 4
#> ATC:skmeans 72 0.1626 1.09e-25 0.60925 4
#> SD:mclust 74 0.5018 4.27e-21 0.90590 4
#> CV:mclust 70 0.3723 1.20e-22 0.10605 4
#> MAD:mclust 71 0.7364 2.56e-23 0.18884 4
#> ATC:mclust 75 0.2099 1.76e-19 0.16772 4
#> SD:kmeans 66 0.4227 2.94e-24 0.71408 4
#> CV:kmeans 72 0.3423 1.69e-25 0.15501 4
#> MAD:kmeans 72 0.3256 3.90e-24 0.25389 4
#> ATC:kmeans 75 0.2646 2.89e-19 0.44684 4
#> SD:pam 69 0.1834 1.03e-16 0.00576 4
#> CV:pam 73 0.7474 7.51e-24 0.04395 4
#> MAD:pam 70 0.2750 1.96e-15 0.02975 4
#> ATC:pam 78 0.1833 4.73e-22 0.53512 4
#> SD:hclust 66 0.2876 4.59e-14 0.79873 4
#> CV:hclust 65 0.3123 5.44e-14 0.01789 4
#> MAD:hclust 66 0.6648 1.55e-17 0.06118 4
#> ATC:hclust 64 0.4528 1.84e-14 0.03096 4
test_to_known_factors(res_list, k = 5)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 68 0.261 5.31e-19 0.0242 5
#> CV:NMF 70 0.575 9.71e-26 0.0637 5
#> MAD:NMF 59 0.199 1.91e-17 0.1844 5
#> ATC:NMF 57 0.654 2.96e-22 0.2243 5
#> SD:skmeans 68 0.671 3.95e-19 0.0420 5
#> CV:skmeans 73 0.735 8.34e-25 0.1230 5
#> MAD:skmeans 76 0.781 2.52e-23 0.0193 5
#> ATC:skmeans 75 0.427 1.44e-25 0.7891 5
#> SD:mclust 76 0.397 1.02e-22 0.0388 5
#> CV:mclust 73 0.550 1.45e-21 0.0642 5
#> MAD:mclust 71 0.420 1.23e-21 0.1609 5
#> ATC:mclust 66 0.321 4.27e-17 0.0865 5
#> SD:kmeans 73 0.429 8.46e-22 0.0364 5
#> CV:kmeans 74 0.775 2.30e-23 0.1506 5
#> MAD:kmeans 71 0.744 1.55e-22 0.0544 5
#> ATC:kmeans 73 0.722 8.23e-24 0.0626 5
#> SD:pam 67 0.524 6.28e-20 0.0215 5
#> CV:pam 60 0.870 1.94e-19 0.0249 5
#> MAD:pam 67 0.576 4.23e-20 0.0279 5
#> ATC:pam 78 0.795 1.74e-24 0.0730 5
#> SD:hclust 76 0.375 2.60e-13 0.0393 5
#> CV:hclust 75 0.308 8.94e-23 0.1384 5
#> MAD:hclust 55 0.910 3.22e-13 0.0673 5
#> ATC:hclust 68 0.474 1.77e-13 0.0339 5
test_to_known_factors(res_list, k = 6)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 57 0.1003 7.15e-17 0.0111 6
#> CV:NMF 65 0.3239 1.27e-21 0.0357 6
#> MAD:NMF 52 0.2631 4.56e-17 0.0897 6
#> ATC:NMF 45 0.5663 3.03e-17 0.2842 6
#> SD:skmeans 63 0.5466 2.17e-16 0.0153 6
#> CV:skmeans 65 0.9612 9.07e-21 0.1584 6
#> MAD:skmeans 60 0.8856 2.58e-18 0.0403 6
#> ATC:skmeans 70 0.4324 1.37e-23 0.5970 6
#> SD:mclust 72 0.7924 2.80e-20 0.0440 6
#> CV:mclust 74 0.7292 2.77e-21 0.0637 6
#> MAD:mclust 71 0.8501 5.27e-21 0.0872 6
#> ATC:mclust 78 0.0846 1.61e-19 0.1093 6
#> SD:kmeans 57 0.5790 2.41e-17 0.0172 6
#> CV:kmeans 69 0.7200 3.03e-21 0.0987 6
#> MAD:kmeans 72 0.8708 1.08e-21 0.0178 6
#> ATC:kmeans 71 0.6291 4.36e-23 0.1207 6
#> SD:pam 68 0.5169 3.34e-17 0.0444 6
#> CV:pam 58 0.9386 4.16e-18 0.0411 6
#> MAD:pam 63 0.7295 1.10e-18 0.0209 6
#> ATC:pam 78 0.8282 3.33e-23 0.0767 6
#> SD:hclust 74 0.5625 1.34e-17 0.0174 6
#> CV:hclust 76 0.2881 1.30e-20 0.1029 6
#> MAD:hclust 54 0.3198 1.56e-16 0.0672 6
#> ATC:hclust 70 0.6195 8.27e-13 0.0323 6
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "hclust"]
# you can also extract it by
# res = res_list["SD:hclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'hclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
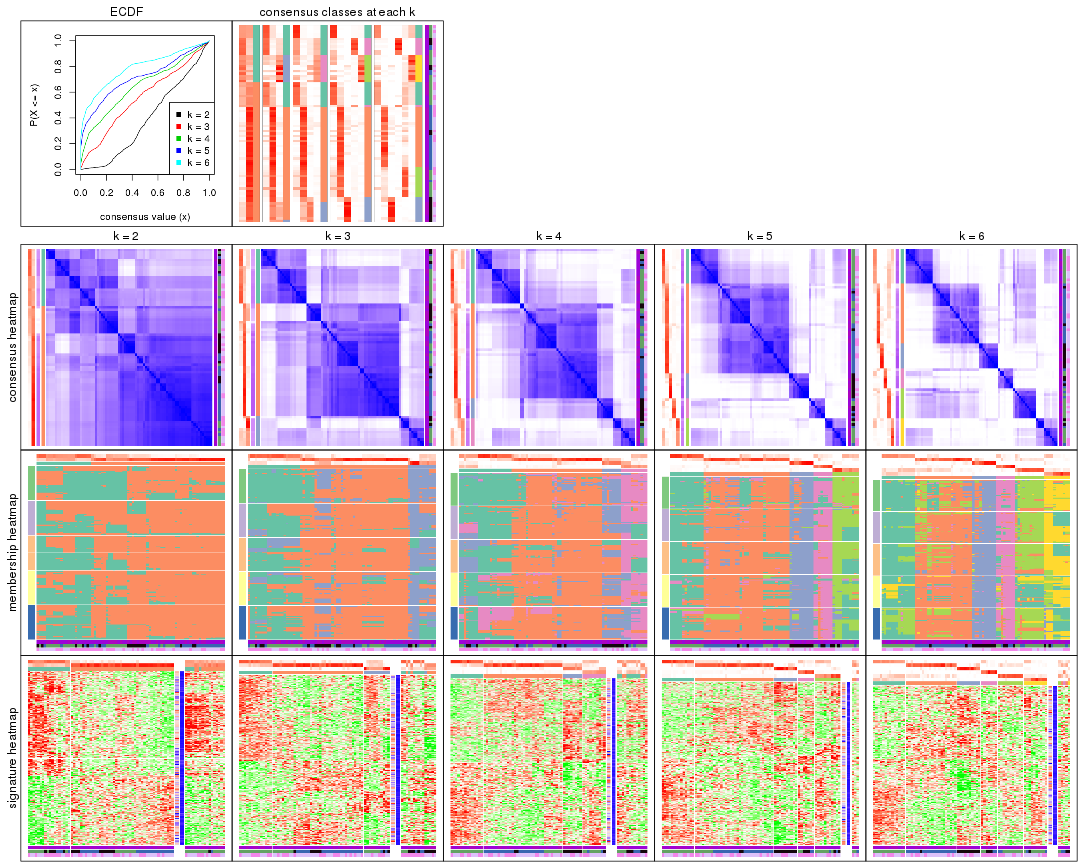
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
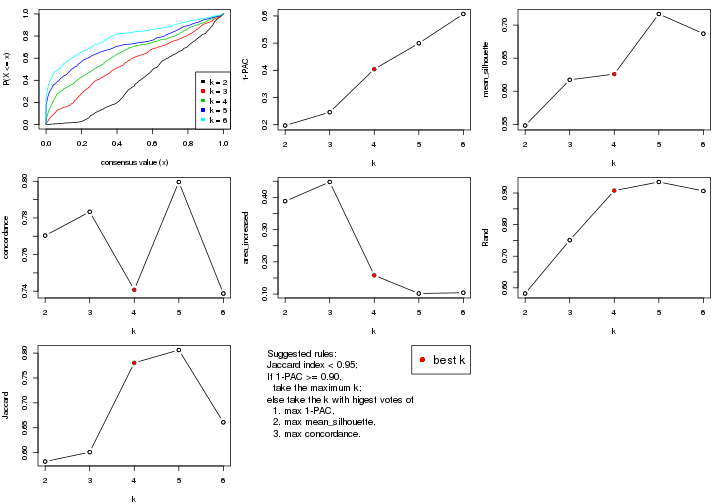
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.197 0.548 0.770 0.388 0.582 0.582
#> 3 3 0.246 0.617 0.783 0.448 0.751 0.601
#> 4 4 0.404 0.626 0.741 0.158 0.908 0.781
#> 5 5 0.499 0.717 0.800 0.102 0.935 0.806
#> 6 6 0.607 0.687 0.739 0.104 0.907 0.661
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.7453 5.66e-01 0.212 0.788
#> GSM907859 1 0.8763 6.25e-01 0.704 0.296
#> GSM907860 2 0.6712 6.15e-01 0.176 0.824
#> GSM907854 2 0.7376 5.60e-01 0.208 0.792
#> GSM907855 2 0.7453 5.66e-01 0.212 0.788
#> GSM907856 2 0.7453 5.66e-01 0.212 0.788
#> GSM907857 2 0.8813 4.56e-01 0.300 0.700
#> GSM907825 2 0.1633 7.49e-01 0.024 0.976
#> GSM907828 2 0.4431 7.30e-01 0.092 0.908
#> GSM907832 2 0.2043 7.52e-01 0.032 0.968
#> GSM907833 2 0.1414 7.52e-01 0.020 0.980
#> GSM907834 2 0.1414 7.49e-01 0.020 0.980
#> GSM907826 2 0.2423 7.41e-01 0.040 0.960
#> GSM907827 2 0.2603 7.51e-01 0.044 0.956
#> GSM907829 2 0.5294 7.00e-01 0.120 0.880
#> GSM907830 2 0.7139 6.12e-01 0.196 0.804
#> GSM907831 2 0.3733 7.21e-01 0.072 0.928
#> GSM907792 2 0.9866 -1.90e-01 0.432 0.568
#> GSM907795 1 0.9993 4.22e-01 0.516 0.484
#> GSM907801 2 0.9963 -3.07e-01 0.464 0.536
#> GSM907802 2 0.2423 7.49e-01 0.040 0.960
#> GSM907804 2 0.3274 7.39e-01 0.060 0.940
#> GSM907805 1 0.9909 5.42e-01 0.556 0.444
#> GSM907806 2 0.9491 8.52e-02 0.368 0.632
#> GSM907793 1 0.9998 4.02e-01 0.508 0.492
#> GSM907794 2 0.6343 6.41e-01 0.160 0.840
#> GSM907796 1 0.9933 5.08e-01 0.548 0.452
#> GSM907797 1 0.9580 5.81e-01 0.620 0.380
#> GSM907798 1 0.9833 5.39e-01 0.576 0.424
#> GSM907799 2 0.9580 3.87e-02 0.380 0.620
#> GSM907800 2 0.2043 7.50e-01 0.032 0.968
#> GSM907803 2 0.9635 2.55e-05 0.388 0.612
#> GSM907864 1 0.8207 6.34e-01 0.744 0.256
#> GSM907865 1 0.7674 6.32e-01 0.776 0.224
#> GSM907868 2 0.7376 5.72e-01 0.208 0.792
#> GSM907869 1 0.8661 5.08e-01 0.712 0.288
#> GSM907870 2 0.6712 6.10e-01 0.176 0.824
#> GSM907861 2 0.5629 6.57e-01 0.132 0.868
#> GSM907862 2 0.3733 7.43e-01 0.072 0.928
#> GSM907863 2 0.3733 7.43e-01 0.072 0.928
#> GSM907866 1 0.7745 5.42e-01 0.772 0.228
#> GSM907867 2 0.3431 7.25e-01 0.064 0.936
#> GSM907839 1 0.8207 6.34e-01 0.744 0.256
#> GSM907840 1 0.7745 6.34e-01 0.772 0.228
#> GSM907842 2 0.9954 -3.01e-01 0.460 0.540
#> GSM907843 2 0.5946 6.46e-01 0.144 0.856
#> GSM907845 1 0.9954 5.06e-01 0.540 0.460
#> GSM907846 2 0.2423 7.49e-01 0.040 0.960
#> GSM907848 2 0.1414 7.52e-01 0.020 0.980
#> GSM907851 2 0.6712 6.01e-01 0.176 0.824
#> GSM907835 2 0.1633 7.52e-01 0.024 0.976
#> GSM907836 2 0.2236 7.42e-01 0.036 0.964
#> GSM907837 2 0.1843 7.50e-01 0.028 0.972
#> GSM907838 2 0.1843 7.50e-01 0.028 0.972
#> GSM907841 1 0.7745 5.42e-01 0.772 0.228
#> GSM907844 2 0.2603 7.38e-01 0.044 0.956
#> GSM907847 2 0.1633 7.51e-01 0.024 0.976
#> GSM907849 2 0.4815 6.90e-01 0.104 0.896
#> GSM907850 2 0.1414 7.52e-01 0.020 0.980
#> GSM907852 2 0.0672 7.52e-01 0.008 0.992
#> GSM907853 2 0.1633 7.51e-01 0.024 0.976
#> GSM907807 1 0.9993 4.22e-01 0.516 0.484
#> GSM907813 1 0.7674 6.29e-01 0.776 0.224
#> GSM907814 1 0.7376 6.26e-01 0.792 0.208
#> GSM907816 2 0.9988 -3.23e-01 0.480 0.520
#> GSM907818 1 0.9944 5.15e-01 0.544 0.456
#> GSM907819 2 0.3431 7.32e-01 0.064 0.936
#> GSM907820 2 0.2043 7.50e-01 0.032 0.968
#> GSM907822 2 0.9608 2.75e-02 0.384 0.616
#> GSM907823 2 0.8555 3.90e-01 0.280 0.720
#> GSM907808 1 0.9983 4.32e-01 0.524 0.476
#> GSM907809 1 0.9983 4.32e-01 0.524 0.476
#> GSM907810 2 0.9608 2.75e-02 0.384 0.616
#> GSM907811 2 0.9552 5.46e-02 0.376 0.624
#> GSM907812 1 0.9833 5.39e-01 0.576 0.424
#> GSM907815 1 0.7674 5.45e-01 0.776 0.224
#> GSM907817 2 0.2043 7.50e-01 0.032 0.968
#> GSM907821 2 0.3114 7.41e-01 0.056 0.944
#> GSM907824 2 0.1843 7.51e-01 0.028 0.972
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 2 0.6204 0.3281 0.000 0.576 0.424
#> GSM907859 1 0.7228 0.4874 0.708 0.104 0.188
#> GSM907860 2 0.5873 0.5308 0.004 0.684 0.312
#> GSM907854 2 0.6180 0.3386 0.000 0.584 0.416
#> GSM907855 2 0.6204 0.3281 0.000 0.576 0.424
#> GSM907856 2 0.6204 0.3281 0.000 0.576 0.424
#> GSM907857 3 0.6307 -0.1828 0.000 0.488 0.512
#> GSM907825 2 0.0747 0.7963 0.000 0.984 0.016
#> GSM907828 2 0.3918 0.7609 0.120 0.868 0.012
#> GSM907832 2 0.2947 0.7882 0.060 0.920 0.020
#> GSM907833 2 0.1529 0.8028 0.040 0.960 0.000
#> GSM907834 2 0.0592 0.7969 0.000 0.988 0.012
#> GSM907826 2 0.2280 0.7957 0.008 0.940 0.052
#> GSM907827 2 0.2116 0.7992 0.012 0.948 0.040
#> GSM907829 2 0.3983 0.7439 0.004 0.852 0.144
#> GSM907830 2 0.6374 0.6752 0.100 0.768 0.132
#> GSM907831 2 0.2537 0.7843 0.000 0.920 0.080
#> GSM907792 1 0.5580 0.6352 0.736 0.256 0.008
#> GSM907795 1 0.4002 0.6403 0.840 0.160 0.000
#> GSM907801 1 0.4931 0.6451 0.784 0.212 0.004
#> GSM907802 2 0.3886 0.7654 0.096 0.880 0.024
#> GSM907804 2 0.4280 0.7436 0.124 0.856 0.020
#> GSM907805 3 0.9480 0.5294 0.268 0.236 0.496
#> GSM907806 1 0.7104 0.5393 0.608 0.360 0.032
#> GSM907793 1 0.4121 0.6423 0.832 0.168 0.000
#> GSM907794 2 0.7065 0.5486 0.228 0.700 0.072
#> GSM907796 3 0.9616 0.5034 0.296 0.236 0.468
#> GSM907797 3 0.8210 0.5766 0.240 0.132 0.628
#> GSM907798 3 0.9231 0.5350 0.300 0.184 0.516
#> GSM907799 1 0.6381 0.5843 0.648 0.340 0.012
#> GSM907800 2 0.3610 0.7668 0.096 0.888 0.016
#> GSM907803 1 0.6307 0.5959 0.660 0.328 0.012
#> GSM907864 1 0.6537 0.4771 0.740 0.064 0.196
#> GSM907865 1 0.5803 0.4608 0.760 0.028 0.212
#> GSM907868 2 0.6180 0.3468 0.000 0.584 0.416
#> GSM907869 3 0.2496 0.5640 0.004 0.068 0.928
#> GSM907870 2 0.5517 0.5514 0.268 0.728 0.004
#> GSM907861 2 0.5754 0.5401 0.004 0.700 0.296
#> GSM907862 2 0.4662 0.7397 0.032 0.844 0.124
#> GSM907863 2 0.4662 0.7397 0.032 0.844 0.124
#> GSM907866 3 0.0424 0.5645 0.000 0.008 0.992
#> GSM907867 2 0.2860 0.7821 0.004 0.912 0.084
#> GSM907839 1 0.6537 0.4771 0.740 0.064 0.196
#> GSM907840 1 0.5874 0.4641 0.760 0.032 0.208
#> GSM907842 1 0.9008 0.3820 0.500 0.360 0.140
#> GSM907843 2 0.5070 0.6273 0.224 0.772 0.004
#> GSM907845 3 0.9380 0.5525 0.232 0.256 0.512
#> GSM907846 2 0.3921 0.7663 0.112 0.872 0.016
#> GSM907848 2 0.1529 0.8028 0.040 0.960 0.000
#> GSM907851 2 0.5656 0.5287 0.284 0.712 0.004
#> GSM907835 2 0.1525 0.8030 0.032 0.964 0.004
#> GSM907836 2 0.2173 0.7963 0.008 0.944 0.048
#> GSM907837 2 0.1163 0.8023 0.028 0.972 0.000
#> GSM907838 2 0.1163 0.8023 0.028 0.972 0.000
#> GSM907841 3 0.0424 0.5645 0.000 0.008 0.992
#> GSM907844 2 0.2200 0.7926 0.004 0.940 0.056
#> GSM907847 2 0.1753 0.8019 0.048 0.952 0.000
#> GSM907849 2 0.4178 0.7027 0.172 0.828 0.000
#> GSM907850 2 0.1765 0.8031 0.040 0.956 0.004
#> GSM907852 2 0.0592 0.8003 0.012 0.988 0.000
#> GSM907853 2 0.1753 0.8019 0.048 0.952 0.000
#> GSM907807 1 0.4002 0.6403 0.840 0.160 0.000
#> GSM907813 1 0.4682 0.4741 0.804 0.004 0.192
#> GSM907814 1 0.4883 0.4591 0.788 0.004 0.208
#> GSM907816 1 0.6066 0.6259 0.728 0.248 0.024
#> GSM907818 3 0.9357 0.5577 0.236 0.248 0.516
#> GSM907819 2 0.4413 0.7476 0.104 0.860 0.036
#> GSM907820 2 0.3610 0.7668 0.096 0.888 0.016
#> GSM907822 1 0.6357 0.5881 0.652 0.336 0.012
#> GSM907823 2 0.6625 0.0885 0.440 0.552 0.008
#> GSM907808 1 0.4862 0.6309 0.820 0.160 0.020
#> GSM907809 1 0.4862 0.6309 0.820 0.160 0.020
#> GSM907810 1 0.6307 0.5947 0.660 0.328 0.012
#> GSM907811 1 0.6404 0.5801 0.644 0.344 0.012
#> GSM907812 3 0.9231 0.5350 0.300 0.184 0.516
#> GSM907815 3 0.0475 0.5643 0.004 0.004 0.992
#> GSM907817 2 0.3610 0.7668 0.096 0.888 0.016
#> GSM907821 2 0.4289 0.7570 0.092 0.868 0.040
#> GSM907824 2 0.3459 0.7691 0.096 0.892 0.012
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.4477 0.919 0.000 0.312 0.688 0.000
#> GSM907859 1 0.8243 0.490 0.492 0.088 0.088 0.332
#> GSM907860 3 0.5582 0.795 0.000 0.400 0.576 0.024
#> GSM907854 3 0.4720 0.915 0.000 0.324 0.672 0.004
#> GSM907855 3 0.4477 0.919 0.000 0.312 0.688 0.000
#> GSM907856 3 0.4477 0.919 0.000 0.312 0.688 0.000
#> GSM907857 3 0.5309 0.810 0.000 0.256 0.700 0.044
#> GSM907825 2 0.1284 0.741 0.000 0.964 0.024 0.012
#> GSM907828 2 0.4033 0.706 0.112 0.840 0.040 0.008
#> GSM907832 2 0.2958 0.743 0.072 0.896 0.004 0.028
#> GSM907833 2 0.1488 0.758 0.032 0.956 0.012 0.000
#> GSM907834 2 0.1151 0.741 0.000 0.968 0.024 0.008
#> GSM907826 2 0.2125 0.726 0.000 0.920 0.076 0.004
#> GSM907827 2 0.2741 0.713 0.012 0.892 0.096 0.000
#> GSM907829 2 0.4549 0.637 0.008 0.816 0.076 0.100
#> GSM907830 2 0.6491 0.563 0.064 0.716 0.100 0.120
#> GSM907831 2 0.3047 0.689 0.000 0.872 0.116 0.012
#> GSM907792 1 0.3306 0.607 0.840 0.156 0.000 0.004
#> GSM907795 1 0.1733 0.559 0.948 0.028 0.000 0.024
#> GSM907801 1 0.2408 0.603 0.896 0.104 0.000 0.000
#> GSM907802 2 0.3986 0.714 0.132 0.832 0.004 0.032
#> GSM907804 2 0.4381 0.694 0.160 0.804 0.008 0.028
#> GSM907805 4 0.8048 0.660 0.356 0.116 0.048 0.480
#> GSM907806 1 0.5022 0.535 0.708 0.264 0.000 0.028
#> GSM907793 1 0.1929 0.561 0.940 0.036 0.000 0.024
#> GSM907794 2 0.6389 0.465 0.300 0.620 0.008 0.072
#> GSM907796 4 0.7734 0.632 0.396 0.100 0.036 0.468
#> GSM907797 4 0.7025 0.689 0.316 0.020 0.088 0.576
#> GSM907798 4 0.7163 0.660 0.400 0.052 0.040 0.508
#> GSM907799 1 0.4328 0.577 0.748 0.244 0.000 0.008
#> GSM907800 2 0.3842 0.714 0.136 0.836 0.004 0.024
#> GSM907803 1 0.4228 0.586 0.760 0.232 0.000 0.008
#> GSM907864 1 0.7686 0.481 0.508 0.040 0.096 0.356
#> GSM907865 1 0.7071 0.463 0.504 0.004 0.112 0.380
#> GSM907868 3 0.4522 0.917 0.000 0.320 0.680 0.000
#> GSM907869 4 0.6187 0.492 0.000 0.052 0.432 0.516
#> GSM907870 2 0.4452 0.591 0.260 0.732 0.000 0.008
#> GSM907861 3 0.5151 0.717 0.000 0.464 0.532 0.004
#> GSM907862 2 0.6338 -0.352 0.024 0.568 0.380 0.028
#> GSM907863 2 0.6338 -0.352 0.024 0.568 0.380 0.028
#> GSM907866 4 0.5060 0.576 0.000 0.004 0.412 0.584
#> GSM907867 2 0.3157 0.656 0.000 0.852 0.144 0.004
#> GSM907839 1 0.7686 0.481 0.508 0.040 0.096 0.356
#> GSM907840 1 0.7191 0.466 0.504 0.008 0.112 0.376
#> GSM907842 1 0.8802 0.316 0.376 0.356 0.052 0.216
#> GSM907843 2 0.4392 0.623 0.216 0.768 0.012 0.004
#> GSM907845 4 0.8214 0.670 0.320 0.136 0.052 0.492
#> GSM907846 2 0.3873 0.718 0.144 0.832 0.008 0.016
#> GSM907848 2 0.1488 0.758 0.032 0.956 0.012 0.000
#> GSM907851 2 0.4567 0.575 0.276 0.716 0.000 0.008
#> GSM907835 2 0.1629 0.754 0.024 0.952 0.024 0.000
#> GSM907836 2 0.2125 0.726 0.000 0.920 0.076 0.004
#> GSM907837 2 0.2207 0.746 0.024 0.932 0.040 0.004
#> GSM907838 2 0.2207 0.746 0.024 0.932 0.040 0.004
#> GSM907841 4 0.5060 0.576 0.000 0.004 0.412 0.584
#> GSM907844 2 0.2593 0.700 0.000 0.892 0.104 0.004
#> GSM907847 2 0.1913 0.756 0.040 0.940 0.020 0.000
#> GSM907849 2 0.3764 0.677 0.172 0.816 0.012 0.000
#> GSM907850 2 0.1724 0.757 0.032 0.948 0.020 0.000
#> GSM907852 2 0.0657 0.751 0.004 0.984 0.012 0.000
#> GSM907853 2 0.1913 0.756 0.040 0.940 0.020 0.000
#> GSM907807 1 0.1388 0.566 0.960 0.028 0.000 0.012
#> GSM907813 1 0.6872 0.497 0.564 0.008 0.096 0.332
#> GSM907814 1 0.6888 0.487 0.556 0.004 0.108 0.332
#> GSM907816 1 0.5509 0.606 0.744 0.180 0.016 0.060
#> GSM907818 4 0.8122 0.677 0.328 0.124 0.052 0.496
#> GSM907819 2 0.4456 0.690 0.148 0.804 0.004 0.044
#> GSM907820 2 0.3842 0.714 0.136 0.836 0.004 0.024
#> GSM907822 1 0.4295 0.580 0.752 0.240 0.000 0.008
#> GSM907823 2 0.5277 0.212 0.460 0.532 0.000 0.008
#> GSM907808 1 0.2023 0.552 0.940 0.028 0.004 0.028
#> GSM907809 1 0.2023 0.552 0.940 0.028 0.004 0.028
#> GSM907810 1 0.4228 0.586 0.760 0.232 0.000 0.008
#> GSM907811 1 0.4360 0.575 0.744 0.248 0.000 0.008
#> GSM907812 4 0.7163 0.660 0.400 0.052 0.040 0.508
#> GSM907815 4 0.4888 0.579 0.000 0.000 0.412 0.588
#> GSM907817 2 0.3842 0.714 0.136 0.836 0.004 0.024
#> GSM907821 2 0.4336 0.701 0.132 0.816 0.004 0.048
#> GSM907824 2 0.3828 0.720 0.132 0.840 0.008 0.020
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0162 0.851 0.000 0.000 0.996 0.000 0.004
#> GSM907859 4 0.4504 0.754 0.168 0.084 0.000 0.748 0.000
#> GSM907860 3 0.2795 0.815 0.000 0.060 0.892 0.024 0.024
#> GSM907854 3 0.0693 0.851 0.000 0.012 0.980 0.000 0.008
#> GSM907855 3 0.0162 0.851 0.000 0.000 0.996 0.000 0.004
#> GSM907856 3 0.0162 0.851 0.000 0.000 0.996 0.000 0.004
#> GSM907857 3 0.1908 0.788 0.000 0.000 0.908 0.000 0.092
#> GSM907825 2 0.2544 0.791 0.000 0.900 0.064 0.008 0.028
#> GSM907828 2 0.4440 0.765 0.100 0.808 0.048 0.028 0.016
#> GSM907832 2 0.3161 0.775 0.100 0.860 0.000 0.032 0.008
#> GSM907833 2 0.2027 0.803 0.040 0.928 0.008 0.024 0.000
#> GSM907834 2 0.2456 0.792 0.000 0.904 0.064 0.008 0.024
#> GSM907826 2 0.2729 0.793 0.004 0.884 0.084 0.000 0.028
#> GSM907827 2 0.4063 0.750 0.008 0.808 0.140 0.020 0.024
#> GSM907829 2 0.5261 0.692 0.008 0.736 0.120 0.020 0.116
#> GSM907830 2 0.6185 0.620 0.020 0.668 0.080 0.192 0.040
#> GSM907831 2 0.3888 0.725 0.000 0.788 0.176 0.004 0.032
#> GSM907792 1 0.2969 0.784 0.852 0.128 0.000 0.020 0.000
#> GSM907795 1 0.1741 0.674 0.936 0.000 0.000 0.024 0.040
#> GSM907801 1 0.2585 0.760 0.896 0.072 0.000 0.024 0.008
#> GSM907802 2 0.3934 0.736 0.160 0.796 0.000 0.036 0.008
#> GSM907804 2 0.4100 0.707 0.192 0.764 0.000 0.044 0.000
#> GSM907805 5 0.6056 0.642 0.364 0.076 0.000 0.020 0.540
#> GSM907806 1 0.4456 0.742 0.736 0.224 0.000 0.020 0.020
#> GSM907793 1 0.2228 0.685 0.920 0.012 0.000 0.028 0.040
#> GSM907794 2 0.5894 0.382 0.336 0.580 0.000 0.040 0.044
#> GSM907796 5 0.6190 0.600 0.416 0.052 0.000 0.040 0.492
#> GSM907797 5 0.4500 0.683 0.316 0.000 0.004 0.016 0.664
#> GSM907798 5 0.5212 0.634 0.420 0.004 0.000 0.036 0.540
#> GSM907799 1 0.3519 0.775 0.776 0.216 0.000 0.008 0.000
#> GSM907800 2 0.3734 0.732 0.168 0.796 0.000 0.036 0.000
#> GSM907803 1 0.3421 0.783 0.788 0.204 0.000 0.008 0.000
#> GSM907864 4 0.3165 0.799 0.116 0.036 0.000 0.848 0.000
#> GSM907865 4 0.1732 0.777 0.080 0.000 0.000 0.920 0.000
#> GSM907868 3 0.0451 0.852 0.000 0.008 0.988 0.000 0.004
#> GSM907869 5 0.3355 0.501 0.000 0.000 0.184 0.012 0.804
#> GSM907870 2 0.4649 0.640 0.220 0.716 0.000 0.064 0.000
#> GSM907861 3 0.2890 0.768 0.000 0.160 0.836 0.000 0.004
#> GSM907862 3 0.5675 0.643 0.016 0.240 0.672 0.044 0.028
#> GSM907863 3 0.5675 0.643 0.016 0.240 0.672 0.044 0.028
#> GSM907866 5 0.2046 0.595 0.000 0.000 0.068 0.016 0.916
#> GSM907867 2 0.3724 0.723 0.000 0.788 0.184 0.000 0.028
#> GSM907839 4 0.3165 0.799 0.116 0.036 0.000 0.848 0.000
#> GSM907840 4 0.1892 0.780 0.080 0.004 0.000 0.916 0.000
#> GSM907842 4 0.5969 0.377 0.108 0.344 0.004 0.544 0.000
#> GSM907843 2 0.4253 0.681 0.204 0.756 0.008 0.032 0.000
#> GSM907845 5 0.6213 0.652 0.324 0.100 0.000 0.020 0.556
#> GSM907846 2 0.4082 0.738 0.160 0.788 0.008 0.044 0.000
#> GSM907848 2 0.2027 0.803 0.040 0.928 0.008 0.024 0.000
#> GSM907851 2 0.4793 0.621 0.232 0.700 0.000 0.068 0.000
#> GSM907835 2 0.2586 0.802 0.028 0.912 0.024 0.012 0.024
#> GSM907836 2 0.2729 0.793 0.004 0.884 0.084 0.000 0.028
#> GSM907837 2 0.2771 0.798 0.016 0.904 0.032 0.020 0.028
#> GSM907838 2 0.2771 0.798 0.016 0.904 0.032 0.020 0.028
#> GSM907841 5 0.2046 0.595 0.000 0.000 0.068 0.016 0.916
#> GSM907844 2 0.3238 0.760 0.000 0.836 0.136 0.000 0.028
#> GSM907847 2 0.2395 0.803 0.048 0.912 0.016 0.024 0.000
#> GSM907849 2 0.3716 0.729 0.172 0.800 0.008 0.020 0.000
#> GSM907850 2 0.2228 0.804 0.044 0.920 0.020 0.016 0.000
#> GSM907852 2 0.1659 0.802 0.008 0.948 0.016 0.004 0.024
#> GSM907853 2 0.2395 0.803 0.048 0.912 0.016 0.024 0.000
#> GSM907807 1 0.1493 0.681 0.948 0.000 0.000 0.024 0.028
#> GSM907813 4 0.4101 0.660 0.332 0.000 0.000 0.664 0.004
#> GSM907814 4 0.4029 0.678 0.316 0.000 0.000 0.680 0.004
#> GSM907816 1 0.4573 0.737 0.744 0.164 0.000 0.092 0.000
#> GSM907818 5 0.6107 0.659 0.332 0.088 0.000 0.020 0.560
#> GSM907819 2 0.4616 0.706 0.184 0.756 0.004 0.036 0.020
#> GSM907820 2 0.3734 0.732 0.168 0.796 0.000 0.036 0.000
#> GSM907822 1 0.3487 0.777 0.780 0.212 0.000 0.008 0.000
#> GSM907823 2 0.5611 0.217 0.408 0.516 0.000 0.076 0.000
#> GSM907808 1 0.1750 0.669 0.936 0.000 0.000 0.028 0.036
#> GSM907809 1 0.1750 0.669 0.936 0.000 0.000 0.028 0.036
#> GSM907810 1 0.3496 0.782 0.788 0.200 0.000 0.012 0.000
#> GSM907811 1 0.3551 0.771 0.772 0.220 0.000 0.008 0.000
#> GSM907812 5 0.5212 0.634 0.420 0.004 0.000 0.036 0.540
#> GSM907815 5 0.1981 0.596 0.000 0.000 0.064 0.016 0.920
#> GSM907817 2 0.3734 0.732 0.168 0.796 0.000 0.036 0.000
#> GSM907821 2 0.4326 0.724 0.160 0.780 0.000 0.036 0.024
#> GSM907824 2 0.3771 0.743 0.156 0.804 0.004 0.036 0.000
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0260 0.862 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907859 4 0.3739 0.749 0.088 0.056 0.000 0.816 0.040 0.000
#> GSM907860 3 0.2575 0.825 0.004 0.100 0.872 0.024 0.000 0.000
#> GSM907854 3 0.0717 0.864 0.000 0.016 0.976 0.000 0.008 0.000
#> GSM907855 3 0.0508 0.864 0.000 0.012 0.984 0.000 0.000 0.004
#> GSM907856 3 0.0508 0.864 0.000 0.012 0.984 0.000 0.000 0.004
#> GSM907857 3 0.2094 0.807 0.004 0.004 0.912 0.000 0.020 0.060
#> GSM907825 2 0.4177 0.617 0.004 0.720 0.040 0.000 0.232 0.004
#> GSM907828 2 0.4016 0.705 0.084 0.808 0.020 0.020 0.068 0.000
#> GSM907832 5 0.3738 0.528 0.000 0.312 0.000 0.004 0.680 0.004
#> GSM907833 2 0.3357 0.669 0.004 0.764 0.000 0.008 0.224 0.000
#> GSM907834 2 0.4039 0.621 0.004 0.724 0.040 0.000 0.232 0.000
#> GSM907826 2 0.2533 0.735 0.004 0.884 0.056 0.000 0.056 0.000
#> GSM907827 2 0.2001 0.710 0.000 0.900 0.092 0.000 0.004 0.004
#> GSM907829 2 0.6195 0.540 0.004 0.596 0.100 0.000 0.204 0.096
#> GSM907830 2 0.5387 0.586 0.008 0.712 0.040 0.156 0.044 0.040
#> GSM907831 2 0.4704 0.625 0.000 0.696 0.140 0.000 0.160 0.004
#> GSM907792 1 0.5436 0.808 0.572 0.000 0.000 0.000 0.248 0.180
#> GSM907795 1 0.4902 0.725 0.608 0.000 0.000 0.000 0.088 0.304
#> GSM907801 1 0.5246 0.793 0.608 0.000 0.000 0.000 0.180 0.212
#> GSM907802 5 0.2848 0.828 0.000 0.176 0.000 0.000 0.816 0.008
#> GSM907804 5 0.2762 0.834 0.012 0.108 0.000 0.004 0.864 0.012
#> GSM907805 6 0.3371 0.625 0.036 0.020 0.000 0.000 0.116 0.828
#> GSM907806 1 0.5946 0.742 0.464 0.008 0.000 0.000 0.356 0.172
#> GSM907793 1 0.5161 0.732 0.592 0.000 0.000 0.004 0.100 0.304
#> GSM907794 5 0.5166 0.568 0.100 0.072 0.000 0.000 0.704 0.124
#> GSM907796 6 0.3662 0.575 0.044 0.000 0.004 0.000 0.172 0.780
#> GSM907797 6 0.0820 0.658 0.012 0.000 0.000 0.000 0.016 0.972
#> GSM907798 6 0.3044 0.608 0.048 0.000 0.000 0.000 0.116 0.836
#> GSM907799 1 0.5795 0.777 0.500 0.008 0.000 0.000 0.340 0.152
#> GSM907800 5 0.2558 0.850 0.000 0.156 0.000 0.000 0.840 0.004
#> GSM907803 1 0.5767 0.787 0.512 0.008 0.000 0.000 0.328 0.152
#> GSM907864 4 0.2007 0.785 0.032 0.036 0.000 0.920 0.012 0.000
#> GSM907865 4 0.0146 0.766 0.004 0.000 0.000 0.996 0.000 0.000
#> GSM907868 3 0.0458 0.865 0.000 0.016 0.984 0.000 0.000 0.000
#> GSM907869 6 0.6929 0.447 0.256 0.000 0.184 0.000 0.096 0.464
#> GSM907870 2 0.6639 0.145 0.152 0.444 0.000 0.064 0.340 0.000
#> GSM907861 3 0.3210 0.780 0.000 0.152 0.812 0.000 0.036 0.000
#> GSM907862 3 0.4381 0.670 0.004 0.328 0.640 0.024 0.004 0.000
#> GSM907863 3 0.4381 0.670 0.004 0.328 0.640 0.024 0.004 0.000
#> GSM907866 6 0.6003 0.533 0.348 0.000 0.040 0.000 0.104 0.508
#> GSM907867 2 0.3130 0.693 0.004 0.824 0.144 0.000 0.028 0.000
#> GSM907839 4 0.2007 0.785 0.032 0.036 0.000 0.920 0.012 0.000
#> GSM907840 4 0.0551 0.768 0.004 0.004 0.000 0.984 0.008 0.000
#> GSM907842 4 0.5679 0.347 0.036 0.276 0.000 0.588 0.100 0.000
#> GSM907843 2 0.5764 0.531 0.172 0.616 0.000 0.040 0.172 0.000
#> GSM907845 6 0.3049 0.646 0.004 0.048 0.000 0.000 0.104 0.844
#> GSM907846 5 0.2868 0.831 0.004 0.136 0.008 0.008 0.844 0.000
#> GSM907848 2 0.3384 0.666 0.004 0.760 0.000 0.008 0.228 0.000
#> GSM907851 2 0.6754 0.124 0.164 0.424 0.000 0.068 0.344 0.000
#> GSM907835 2 0.2009 0.736 0.008 0.904 0.004 0.000 0.084 0.000
#> GSM907836 2 0.2533 0.735 0.004 0.884 0.056 0.000 0.056 0.000
#> GSM907837 2 0.0748 0.734 0.004 0.976 0.004 0.000 0.016 0.000
#> GSM907838 2 0.0748 0.734 0.004 0.976 0.004 0.000 0.016 0.000
#> GSM907841 6 0.6003 0.533 0.348 0.000 0.040 0.000 0.104 0.508
#> GSM907844 2 0.2604 0.717 0.004 0.872 0.096 0.000 0.028 0.000
#> GSM907847 2 0.3292 0.682 0.008 0.784 0.000 0.008 0.200 0.000
#> GSM907849 2 0.5004 0.589 0.144 0.676 0.000 0.012 0.168 0.000
#> GSM907850 2 0.3261 0.690 0.004 0.792 0.004 0.008 0.192 0.000
#> GSM907852 2 0.3052 0.668 0.004 0.780 0.000 0.000 0.216 0.000
#> GSM907853 2 0.3262 0.684 0.008 0.788 0.000 0.008 0.196 0.000
#> GSM907807 1 0.4854 0.733 0.620 0.000 0.000 0.000 0.088 0.292
#> GSM907813 4 0.3802 0.617 0.312 0.000 0.000 0.676 0.012 0.000
#> GSM907814 4 0.3446 0.638 0.308 0.000 0.000 0.692 0.000 0.000
#> GSM907816 1 0.6925 0.753 0.508 0.016 0.000 0.084 0.252 0.140
#> GSM907818 6 0.2949 0.646 0.008 0.028 0.000 0.000 0.116 0.848
#> GSM907819 5 0.3046 0.834 0.008 0.112 0.004 0.000 0.848 0.028
#> GSM907820 5 0.2520 0.850 0.000 0.152 0.000 0.000 0.844 0.004
#> GSM907822 1 0.5786 0.779 0.504 0.008 0.000 0.000 0.336 0.152
#> GSM907823 5 0.6675 0.130 0.276 0.184 0.000 0.064 0.476 0.000
#> GSM907808 1 0.4932 0.721 0.600 0.000 0.000 0.000 0.088 0.312
#> GSM907809 1 0.4932 0.721 0.600 0.000 0.000 0.000 0.088 0.312
#> GSM907810 1 0.5668 0.786 0.516 0.004 0.000 0.000 0.328 0.152
#> GSM907811 1 0.5803 0.772 0.496 0.008 0.000 0.000 0.344 0.152
#> GSM907812 6 0.3044 0.608 0.048 0.000 0.000 0.000 0.116 0.836
#> GSM907815 6 0.5953 0.532 0.352 0.000 0.036 0.000 0.104 0.508
#> GSM907817 5 0.2558 0.850 0.000 0.156 0.000 0.000 0.840 0.004
#> GSM907821 5 0.2988 0.839 0.000 0.152 0.000 0.000 0.824 0.024
#> GSM907824 5 0.2738 0.837 0.000 0.176 0.000 0.000 0.820 0.004
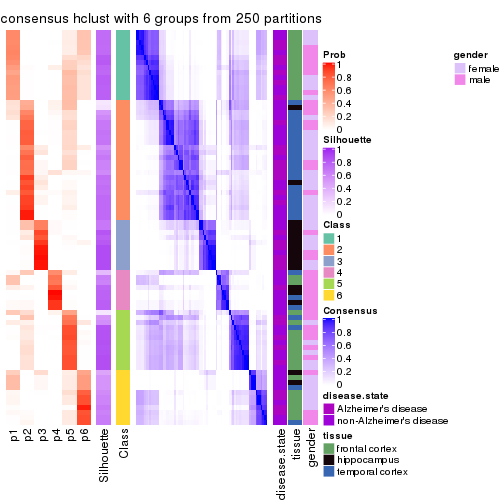
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
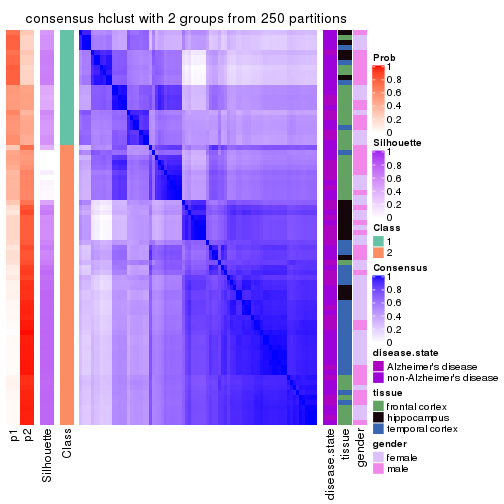
consensus_heatmap(res, k = 3)
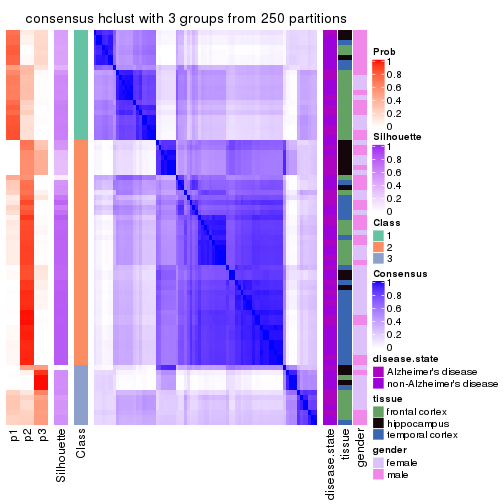
consensus_heatmap(res, k = 4)
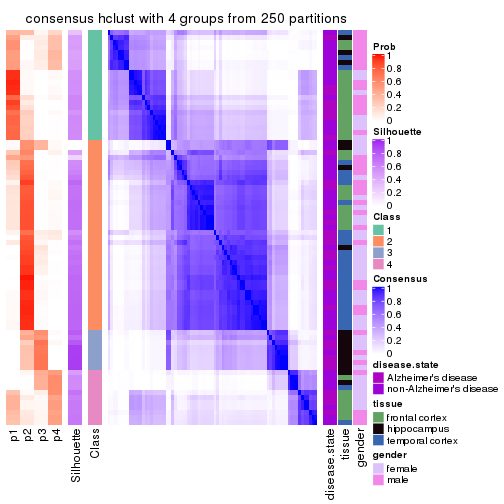
consensus_heatmap(res, k = 5)
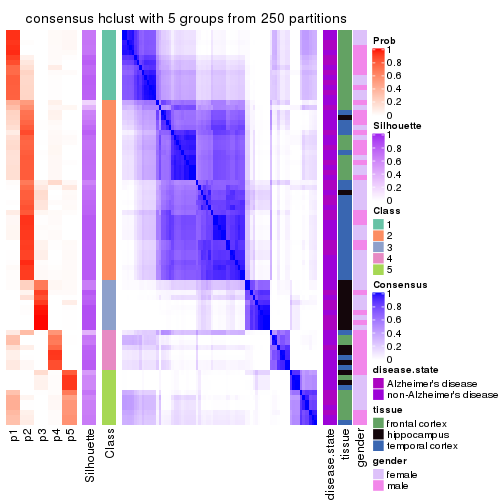
consensus_heatmap(res, k = 6)
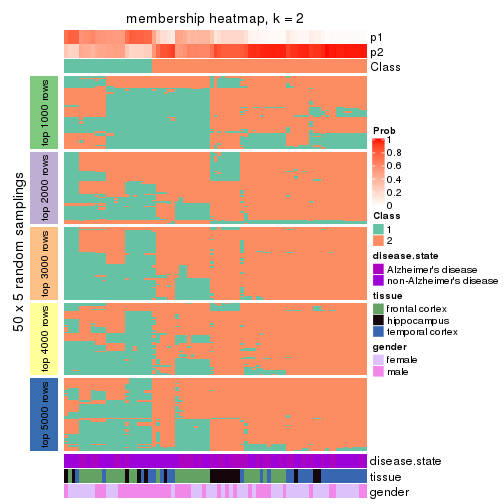
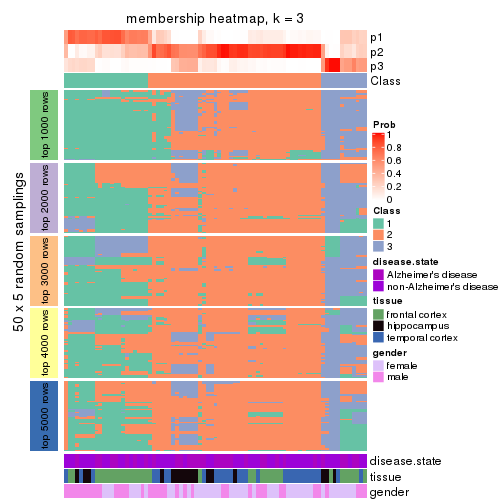
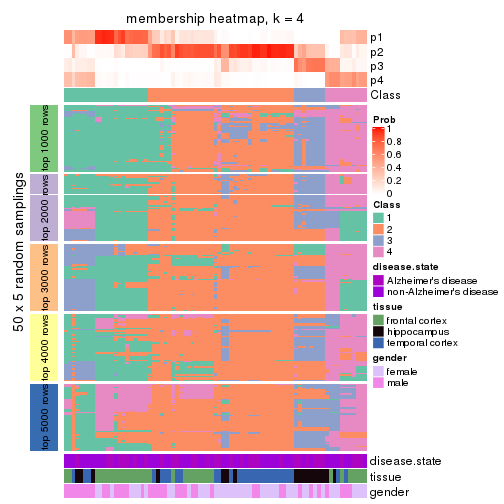
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
membership_heatmap(res, k = 4)
membership_heatmap(res, k = 5)
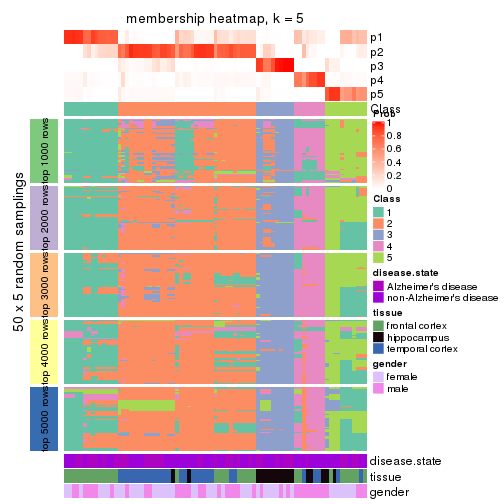
membership_heatmap(res, k = 6)
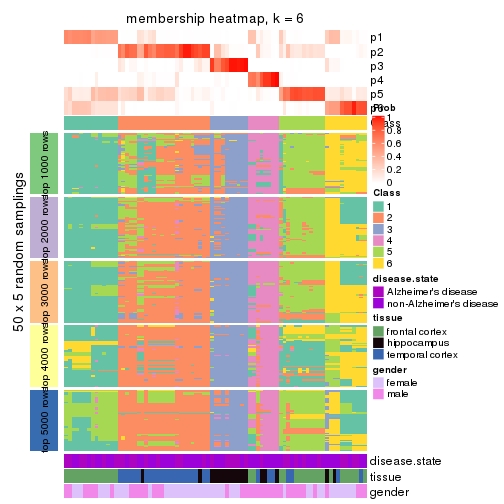
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
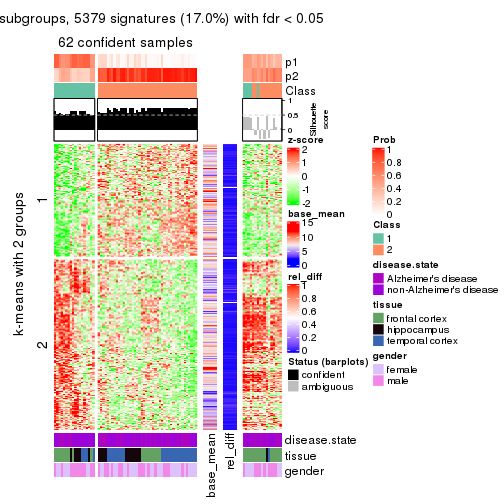
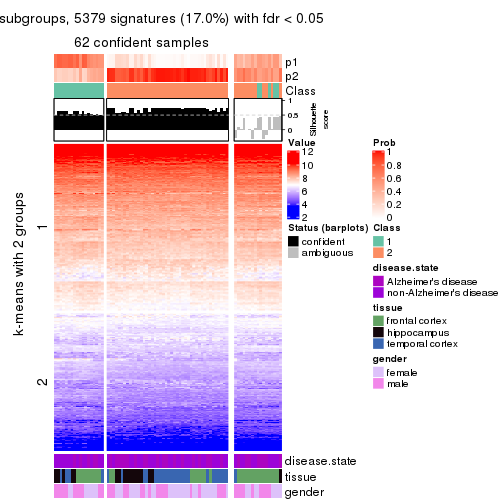
get_signatures(res, k = 2)
get_signatures(res, k = 3)
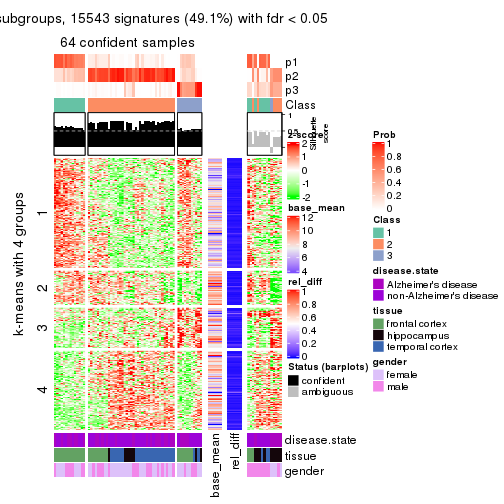
get_signatures(res, k = 4)
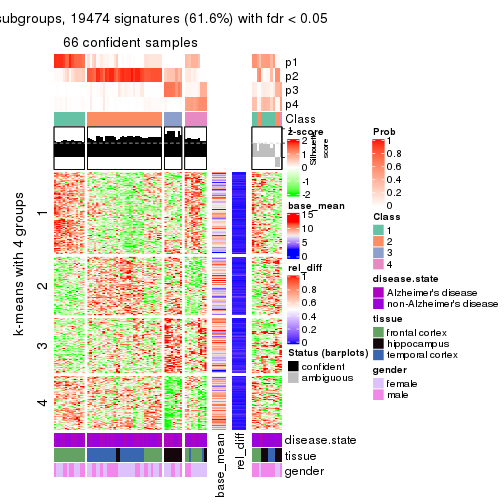
get_signatures(res, k = 5)
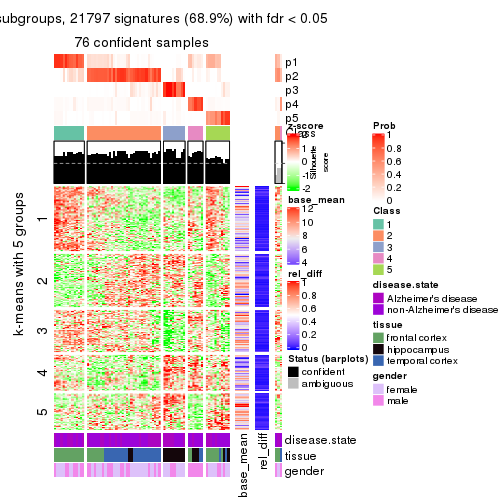
get_signatures(res, k = 6)
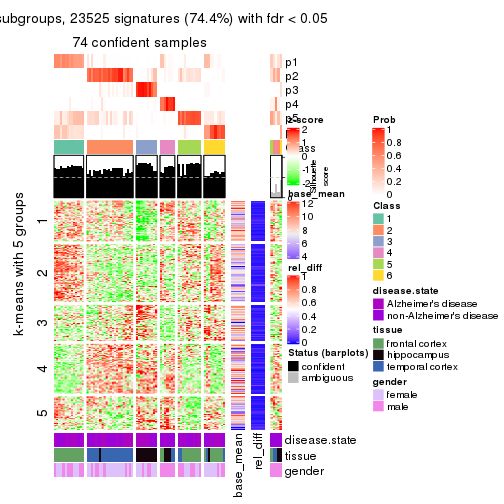
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
get_signatures(res, k = 3, scale_rows = FALSE)
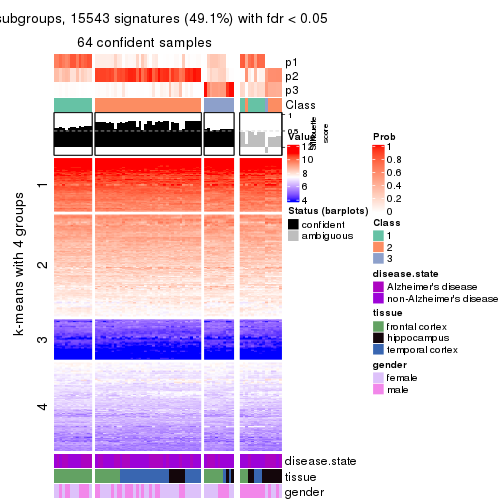
get_signatures(res, k = 4, scale_rows = FALSE)
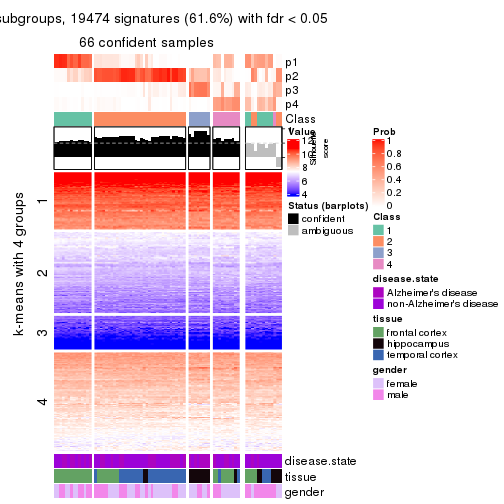
get_signatures(res, k = 5, scale_rows = FALSE)
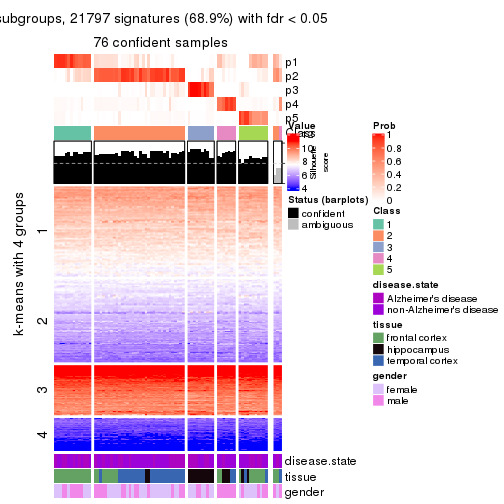
get_signatures(res, k = 6, scale_rows = FALSE)
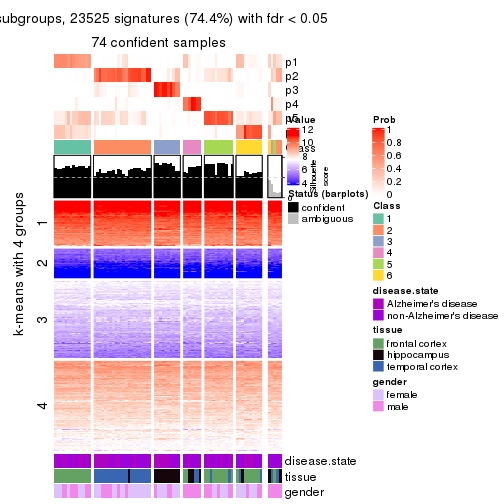
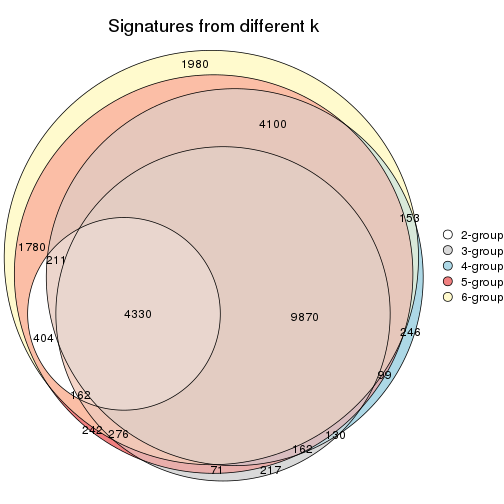
Compare the overlap of signatures from different k:
compare_signatures(res)
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
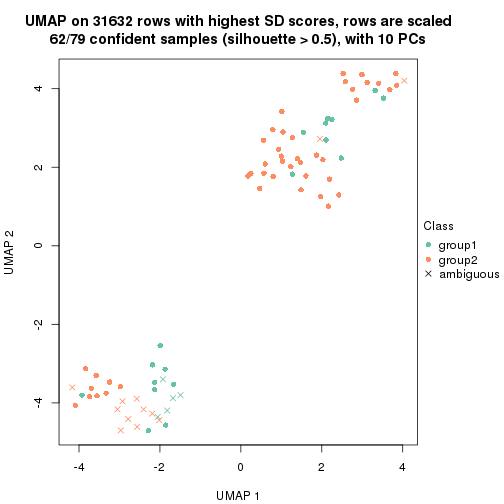
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
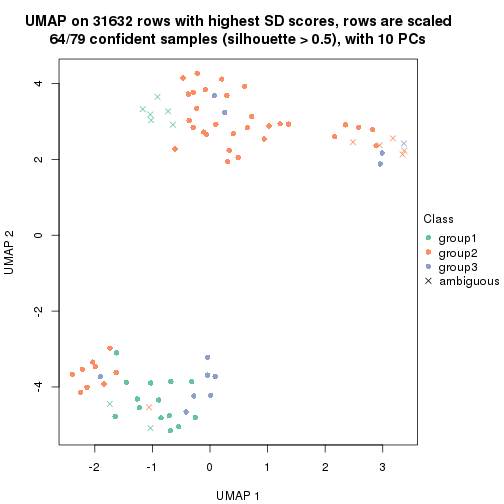
dimension_reduction(res, k = 3, method = "UMAP")
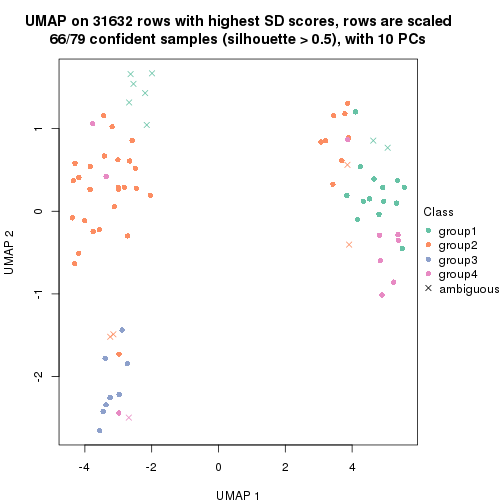
dimension_reduction(res, k = 4, method = "UMAP")
dimension_reduction(res, k = 5, method = "UMAP")
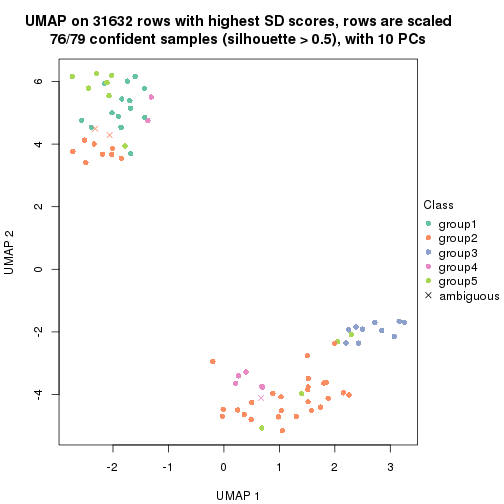
dimension_reduction(res, k = 6, method = "UMAP")
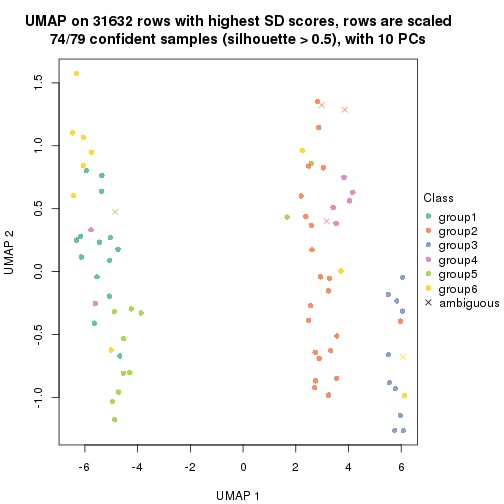
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:hclust 62 0.399 3.28e-02 0.1825 2
#> SD:hclust 64 0.716 1.69e-05 0.7158 3
#> SD:hclust 66 0.288 4.59e-14 0.7987 4
#> SD:hclust 76 0.375 2.60e-13 0.0393 5
#> SD:hclust 74 0.562 1.34e-17 0.0174 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "kmeans"]
# you can also extract it by
# res = res_list["SD:kmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'kmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
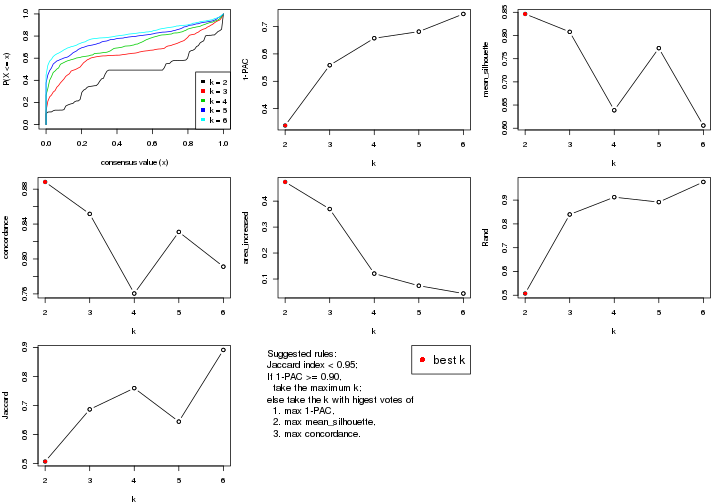
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.338 0.846 0.888 0.4738 0.507 0.507
#> 3 3 0.559 0.808 0.852 0.3696 0.840 0.687
#> 4 4 0.657 0.639 0.760 0.1209 0.912 0.760
#> 5 5 0.681 0.773 0.831 0.0742 0.892 0.645
#> 6 6 0.746 0.606 0.791 0.0441 0.976 0.891
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.829 0.000 1.000
#> GSM907859 2 0.9170 0.756 0.332 0.668
#> GSM907860 2 0.0000 0.829 0.000 1.000
#> GSM907854 2 0.0000 0.829 0.000 1.000
#> GSM907855 2 0.0000 0.829 0.000 1.000
#> GSM907856 2 0.0000 0.829 0.000 1.000
#> GSM907857 2 0.0000 0.829 0.000 1.000
#> GSM907825 2 0.2043 0.834 0.032 0.968
#> GSM907828 2 0.8763 0.786 0.296 0.704
#> GSM907832 2 0.7139 0.838 0.196 0.804
#> GSM907833 2 0.7139 0.838 0.196 0.804
#> GSM907834 2 0.0000 0.829 0.000 1.000
#> GSM907826 2 0.6438 0.842 0.164 0.836
#> GSM907827 2 0.0000 0.829 0.000 1.000
#> GSM907829 2 0.7219 0.834 0.200 0.800
#> GSM907830 2 0.8661 0.790 0.288 0.712
#> GSM907831 2 0.0000 0.829 0.000 1.000
#> GSM907792 1 0.0000 0.924 1.000 0.000
#> GSM907795 1 0.0000 0.924 1.000 0.000
#> GSM907801 1 0.0000 0.924 1.000 0.000
#> GSM907802 1 0.6148 0.844 0.848 0.152
#> GSM907804 1 0.0000 0.924 1.000 0.000
#> GSM907805 1 0.0000 0.924 1.000 0.000
#> GSM907806 1 0.0000 0.924 1.000 0.000
#> GSM907793 1 0.0000 0.924 1.000 0.000
#> GSM907794 1 0.4939 0.884 0.892 0.108
#> GSM907796 1 0.4939 0.884 0.892 0.108
#> GSM907797 1 0.8813 0.671 0.700 0.300
#> GSM907798 1 0.4939 0.884 0.892 0.108
#> GSM907799 1 0.0000 0.924 1.000 0.000
#> GSM907800 1 0.4939 0.884 0.892 0.108
#> GSM907803 1 0.0000 0.924 1.000 0.000
#> GSM907864 2 0.9209 0.752 0.336 0.664
#> GSM907865 2 0.9170 0.755 0.332 0.668
#> GSM907868 2 0.0000 0.829 0.000 1.000
#> GSM907869 2 0.0000 0.829 0.000 1.000
#> GSM907870 2 0.8763 0.786 0.296 0.704
#> GSM907861 2 0.0000 0.829 0.000 1.000
#> GSM907862 2 0.0672 0.828 0.008 0.992
#> GSM907863 2 0.0672 0.828 0.008 0.992
#> GSM907866 2 0.0000 0.829 0.000 1.000
#> GSM907867 2 0.0000 0.829 0.000 1.000
#> GSM907839 2 0.9209 0.752 0.336 0.664
#> GSM907840 2 0.9129 0.760 0.328 0.672
#> GSM907842 2 0.9129 0.760 0.328 0.672
#> GSM907843 2 0.9087 0.764 0.324 0.676
#> GSM907845 2 0.6973 0.840 0.188 0.812
#> GSM907846 2 0.7139 0.838 0.196 0.804
#> GSM907848 2 0.7139 0.838 0.196 0.804
#> GSM907851 2 0.9209 0.752 0.336 0.664
#> GSM907835 2 0.6887 0.841 0.184 0.816
#> GSM907836 2 0.7056 0.839 0.192 0.808
#> GSM907837 2 0.7299 0.837 0.204 0.796
#> GSM907838 2 0.7299 0.837 0.204 0.796
#> GSM907841 2 0.0000 0.829 0.000 1.000
#> GSM907844 2 0.0000 0.829 0.000 1.000
#> GSM907847 2 0.7139 0.838 0.196 0.804
#> GSM907849 2 0.9209 0.752 0.336 0.664
#> GSM907850 2 0.7139 0.838 0.196 0.804
#> GSM907852 2 0.7056 0.839 0.192 0.808
#> GSM907853 2 0.7139 0.838 0.196 0.804
#> GSM907807 1 0.0000 0.924 1.000 0.000
#> GSM907813 1 0.0000 0.924 1.000 0.000
#> GSM907814 1 0.0000 0.924 1.000 0.000
#> GSM907816 1 0.0000 0.924 1.000 0.000
#> GSM907818 1 0.5059 0.881 0.888 0.112
#> GSM907819 1 0.4939 0.884 0.892 0.108
#> GSM907820 1 0.5408 0.872 0.876 0.124
#> GSM907822 1 0.0000 0.924 1.000 0.000
#> GSM907823 1 0.0000 0.924 1.000 0.000
#> GSM907808 1 0.0000 0.924 1.000 0.000
#> GSM907809 1 0.0000 0.924 1.000 0.000
#> GSM907810 1 0.0000 0.924 1.000 0.000
#> GSM907811 1 0.0000 0.924 1.000 0.000
#> GSM907812 1 0.2603 0.911 0.956 0.044
#> GSM907815 1 0.9129 0.636 0.672 0.328
#> GSM907817 1 0.4939 0.884 0.892 0.108
#> GSM907821 1 0.6148 0.844 0.848 0.152
#> GSM907824 1 0.6148 0.844 0.848 0.152
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.3482 0.942 0.000 0.128 0.872
#> GSM907859 2 0.6526 0.689 0.128 0.760 0.112
#> GSM907860 3 0.4399 0.919 0.000 0.188 0.812
#> GSM907854 3 0.3551 0.940 0.000 0.132 0.868
#> GSM907855 3 0.4178 0.927 0.000 0.172 0.828
#> GSM907856 3 0.4178 0.927 0.000 0.172 0.828
#> GSM907857 3 0.3340 0.936 0.000 0.120 0.880
#> GSM907825 2 0.5929 0.503 0.004 0.676 0.320
#> GSM907828 2 0.2486 0.799 0.060 0.932 0.008
#> GSM907832 2 0.3112 0.803 0.004 0.900 0.096
#> GSM907833 2 0.2682 0.811 0.004 0.920 0.076
#> GSM907834 2 0.5785 0.485 0.000 0.668 0.332
#> GSM907826 2 0.3644 0.800 0.004 0.872 0.124
#> GSM907827 2 0.6079 0.359 0.000 0.612 0.388
#> GSM907829 2 0.8227 0.376 0.080 0.536 0.384
#> GSM907830 2 0.2550 0.798 0.040 0.936 0.024
#> GSM907831 2 0.6180 0.308 0.000 0.584 0.416
#> GSM907792 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907795 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907801 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907802 1 0.7777 0.758 0.676 0.160 0.164
#> GSM907804 1 0.4174 0.878 0.872 0.036 0.092
#> GSM907805 1 0.4289 0.878 0.868 0.040 0.092
#> GSM907806 1 0.4709 0.873 0.852 0.056 0.092
#> GSM907793 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907794 1 0.5625 0.860 0.808 0.076 0.116
#> GSM907796 1 0.5875 0.855 0.792 0.072 0.136
#> GSM907797 1 0.7741 0.554 0.568 0.056 0.376
#> GSM907798 1 0.5722 0.859 0.800 0.068 0.132
#> GSM907799 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907800 1 0.5662 0.860 0.808 0.092 0.100
#> GSM907803 1 0.0237 0.886 0.996 0.000 0.004
#> GSM907864 2 0.4799 0.747 0.132 0.836 0.032
#> GSM907865 2 0.8464 0.429 0.132 0.596 0.272
#> GSM907868 3 0.3551 0.941 0.000 0.132 0.868
#> GSM907869 3 0.3267 0.933 0.000 0.116 0.884
#> GSM907870 2 0.2550 0.801 0.056 0.932 0.012
#> GSM907861 3 0.3752 0.937 0.000 0.144 0.856
#> GSM907862 3 0.4887 0.884 0.000 0.228 0.772
#> GSM907863 3 0.4887 0.884 0.000 0.228 0.772
#> GSM907866 3 0.3482 0.942 0.000 0.128 0.872
#> GSM907867 3 0.3879 0.932 0.000 0.152 0.848
#> GSM907839 2 0.4799 0.747 0.132 0.836 0.032
#> GSM907840 2 0.4371 0.765 0.108 0.860 0.032
#> GSM907842 2 0.4371 0.765 0.108 0.860 0.032
#> GSM907843 2 0.4249 0.766 0.108 0.864 0.028
#> GSM907845 2 0.4733 0.751 0.004 0.800 0.196
#> GSM907846 2 0.3851 0.787 0.004 0.860 0.136
#> GSM907848 2 0.2590 0.812 0.004 0.924 0.072
#> GSM907851 2 0.3686 0.769 0.140 0.860 0.000
#> GSM907835 2 0.3030 0.809 0.004 0.904 0.092
#> GSM907836 2 0.3500 0.802 0.004 0.880 0.116
#> GSM907837 2 0.2492 0.808 0.016 0.936 0.048
#> GSM907838 2 0.2492 0.808 0.016 0.936 0.048
#> GSM907841 3 0.3482 0.942 0.000 0.128 0.872
#> GSM907844 2 0.3340 0.801 0.000 0.880 0.120
#> GSM907847 2 0.2590 0.812 0.004 0.924 0.072
#> GSM907849 2 0.3340 0.776 0.120 0.880 0.000
#> GSM907850 2 0.2682 0.812 0.004 0.920 0.076
#> GSM907852 2 0.3030 0.809 0.004 0.904 0.092
#> GSM907853 2 0.2682 0.811 0.004 0.920 0.076
#> GSM907807 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907813 1 0.3310 0.830 0.908 0.064 0.028
#> GSM907814 1 0.2810 0.849 0.928 0.036 0.036
#> GSM907816 1 0.0000 0.886 1.000 0.000 0.000
#> GSM907818 1 0.5897 0.853 0.792 0.076 0.132
#> GSM907819 1 0.5875 0.853 0.792 0.072 0.136
#> GSM907820 1 0.7180 0.795 0.716 0.168 0.116
#> GSM907822 1 0.0000 0.886 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.886 1.000 0.000 0.000
#> GSM907808 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907809 1 0.0592 0.886 0.988 0.000 0.012
#> GSM907810 1 0.0424 0.886 0.992 0.000 0.008
#> GSM907811 1 0.0424 0.885 0.992 0.000 0.008
#> GSM907812 1 0.5094 0.870 0.832 0.056 0.112
#> GSM907815 3 0.3805 0.703 0.092 0.024 0.884
#> GSM907817 1 0.5966 0.852 0.792 0.104 0.104
#> GSM907821 1 0.7766 0.761 0.676 0.148 0.176
#> GSM907824 1 0.7617 0.771 0.688 0.160 0.152
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.5924 0.9041 0.000 0.040 0.556 0.404
#> GSM907859 4 0.6380 0.4593 0.012 0.364 0.048 0.576
#> GSM907860 3 0.5590 0.8882 0.000 0.020 0.524 0.456
#> GSM907854 3 0.5924 0.9041 0.000 0.040 0.556 0.404
#> GSM907855 3 0.5564 0.8950 0.000 0.020 0.544 0.436
#> GSM907856 3 0.5564 0.8950 0.000 0.020 0.544 0.436
#> GSM907857 3 0.5007 0.8793 0.000 0.008 0.636 0.356
#> GSM907825 2 0.4419 0.6956 0.056 0.820 0.008 0.116
#> GSM907828 2 0.3486 0.6625 0.000 0.812 0.000 0.188
#> GSM907832 2 0.0000 0.7994 0.000 1.000 0.000 0.000
#> GSM907833 2 0.0000 0.7994 0.000 1.000 0.000 0.000
#> GSM907834 2 0.4849 0.6731 0.080 0.796 0.008 0.116
#> GSM907826 2 0.1545 0.7949 0.000 0.952 0.008 0.040
#> GSM907827 2 0.4538 0.6400 0.000 0.760 0.024 0.216
#> GSM907829 2 0.7920 0.2985 0.348 0.500 0.100 0.052
#> GSM907830 2 0.4483 0.4710 0.004 0.712 0.000 0.284
#> GSM907831 2 0.4574 0.6184 0.000 0.756 0.024 0.220
#> GSM907792 1 0.4990 0.6935 0.640 0.000 0.352 0.008
#> GSM907795 1 0.5040 0.6908 0.628 0.000 0.364 0.008
#> GSM907801 1 0.4990 0.6935 0.640 0.000 0.352 0.008
#> GSM907802 1 0.4343 0.5326 0.732 0.264 0.004 0.000
#> GSM907804 1 0.0927 0.7088 0.976 0.016 0.008 0.000
#> GSM907805 1 0.1706 0.7087 0.948 0.016 0.036 0.000
#> GSM907806 1 0.1118 0.7053 0.964 0.036 0.000 0.000
#> GSM907793 1 0.5040 0.6908 0.628 0.000 0.364 0.008
#> GSM907794 1 0.1722 0.7006 0.944 0.048 0.008 0.000
#> GSM907796 1 0.3211 0.6898 0.884 0.024 0.084 0.008
#> GSM907797 1 0.4497 0.6440 0.812 0.024 0.140 0.024
#> GSM907798 1 0.3279 0.6908 0.880 0.024 0.088 0.008
#> GSM907799 1 0.4990 0.6935 0.640 0.000 0.352 0.008
#> GSM907800 1 0.2469 0.6748 0.892 0.108 0.000 0.000
#> GSM907803 1 0.4955 0.6936 0.648 0.000 0.344 0.008
#> GSM907864 4 0.6554 0.4520 0.012 0.376 0.056 0.556
#> GSM907865 4 0.6518 0.4609 0.012 0.364 0.056 0.568
#> GSM907868 3 0.5894 0.8993 0.000 0.036 0.536 0.428
#> GSM907869 3 0.5024 0.8776 0.000 0.008 0.632 0.360
#> GSM907870 2 0.3528 0.6574 0.000 0.808 0.000 0.192
#> GSM907861 3 0.6242 0.8851 0.000 0.056 0.520 0.424
#> GSM907862 4 0.6504 -0.7752 0.000 0.072 0.452 0.476
#> GSM907863 4 0.6504 -0.7752 0.000 0.072 0.452 0.476
#> GSM907866 3 0.5558 0.8912 0.000 0.028 0.608 0.364
#> GSM907867 3 0.5912 0.8945 0.000 0.036 0.524 0.440
#> GSM907839 4 0.6554 0.4520 0.012 0.376 0.056 0.556
#> GSM907840 4 0.5353 0.3510 0.012 0.432 0.000 0.556
#> GSM907842 4 0.5360 0.3408 0.012 0.436 0.000 0.552
#> GSM907843 2 0.4019 0.6291 0.012 0.792 0.000 0.196
#> GSM907845 2 0.5899 0.5059 0.256 0.684 0.024 0.036
#> GSM907846 2 0.2773 0.7154 0.116 0.880 0.004 0.000
#> GSM907848 2 0.0000 0.7994 0.000 1.000 0.000 0.000
#> GSM907851 2 0.4646 0.6377 0.044 0.796 0.008 0.152
#> GSM907835 2 0.0817 0.7978 0.000 0.976 0.000 0.024
#> GSM907836 2 0.1635 0.7956 0.000 0.948 0.008 0.044
#> GSM907837 2 0.2760 0.7542 0.000 0.872 0.000 0.128
#> GSM907838 2 0.2760 0.7542 0.000 0.872 0.000 0.128
#> GSM907841 3 0.5587 0.8888 0.000 0.028 0.600 0.372
#> GSM907844 2 0.1489 0.7954 0.000 0.952 0.004 0.044
#> GSM907847 2 0.0188 0.7978 0.000 0.996 0.000 0.004
#> GSM907849 2 0.4321 0.6395 0.024 0.796 0.004 0.176
#> GSM907850 2 0.0000 0.7994 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0817 0.7978 0.000 0.976 0.000 0.024
#> GSM907853 2 0.0000 0.7994 0.000 1.000 0.000 0.000
#> GSM907807 1 0.5040 0.6908 0.628 0.000 0.364 0.008
#> GSM907813 4 0.7455 0.1729 0.148 0.008 0.340 0.504
#> GSM907814 4 0.7551 0.0411 0.196 0.000 0.356 0.448
#> GSM907816 1 0.5093 0.6918 0.640 0.000 0.348 0.012
#> GSM907818 1 0.2949 0.6779 0.888 0.088 0.024 0.000
#> GSM907819 1 0.2363 0.6932 0.920 0.024 0.056 0.000
#> GSM907820 1 0.4193 0.5295 0.732 0.268 0.000 0.000
#> GSM907822 1 0.5093 0.6918 0.640 0.000 0.348 0.012
#> GSM907823 1 0.5093 0.6918 0.640 0.000 0.348 0.012
#> GSM907808 1 0.5040 0.6908 0.628 0.000 0.364 0.008
#> GSM907809 1 0.4905 0.6926 0.632 0.000 0.364 0.004
#> GSM907810 1 0.4990 0.6935 0.640 0.000 0.352 0.008
#> GSM907811 1 0.4917 0.6932 0.656 0.000 0.336 0.008
#> GSM907812 1 0.2853 0.6972 0.900 0.016 0.076 0.008
#> GSM907815 3 0.5986 0.4280 0.320 0.000 0.620 0.060
#> GSM907817 1 0.3569 0.6053 0.804 0.196 0.000 0.000
#> GSM907821 1 0.4343 0.5326 0.732 0.264 0.004 0.000
#> GSM907824 1 0.4343 0.5326 0.732 0.264 0.004 0.000
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0960 0.903 0.000 0.008 0.972 0.004 0.016
#> GSM907859 4 0.3477 0.847 0.040 0.136 0.000 0.824 0.000
#> GSM907860 3 0.0510 0.904 0.000 0.016 0.984 0.000 0.000
#> GSM907854 3 0.0854 0.904 0.000 0.008 0.976 0.004 0.012
#> GSM907855 3 0.0807 0.905 0.000 0.012 0.976 0.000 0.012
#> GSM907856 3 0.0807 0.905 0.000 0.012 0.976 0.000 0.012
#> GSM907857 3 0.4127 0.822 0.000 0.000 0.784 0.080 0.136
#> GSM907825 2 0.4179 0.741 0.000 0.800 0.076 0.012 0.112
#> GSM907828 2 0.3596 0.681 0.000 0.776 0.012 0.212 0.000
#> GSM907832 2 0.2017 0.801 0.000 0.912 0.000 0.008 0.080
#> GSM907833 2 0.2069 0.801 0.000 0.912 0.000 0.012 0.076
#> GSM907834 2 0.4422 0.731 0.000 0.784 0.076 0.016 0.124
#> GSM907826 2 0.1043 0.808 0.000 0.960 0.040 0.000 0.000
#> GSM907827 2 0.3787 0.719 0.000 0.800 0.168 0.012 0.020
#> GSM907829 5 0.6201 0.329 0.004 0.296 0.024 0.088 0.588
#> GSM907830 2 0.4559 0.100 0.000 0.512 0.000 0.480 0.008
#> GSM907831 2 0.4561 0.711 0.000 0.760 0.164 0.012 0.064
#> GSM907792 1 0.0510 0.966 0.984 0.000 0.000 0.000 0.016
#> GSM907795 1 0.0000 0.961 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0510 0.966 0.984 0.000 0.000 0.000 0.016
#> GSM907802 5 0.4680 0.750 0.128 0.132 0.000 0.000 0.740
#> GSM907804 5 0.4162 0.691 0.312 0.004 0.000 0.004 0.680
#> GSM907805 5 0.4718 0.621 0.404 0.008 0.000 0.008 0.580
#> GSM907806 5 0.4492 0.711 0.296 0.020 0.000 0.004 0.680
#> GSM907793 1 0.0000 0.961 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.3920 0.730 0.268 0.004 0.000 0.004 0.724
#> GSM907796 5 0.5512 0.698 0.280 0.000 0.008 0.080 0.632
#> GSM907797 5 0.5386 0.608 0.152 0.000 0.012 0.140 0.696
#> GSM907798 5 0.5624 0.680 0.304 0.000 0.008 0.080 0.608
#> GSM907799 1 0.0510 0.966 0.984 0.000 0.000 0.000 0.016
#> GSM907800 5 0.4906 0.758 0.184 0.092 0.000 0.004 0.720
#> GSM907803 1 0.1197 0.952 0.952 0.000 0.000 0.000 0.048
#> GSM907864 4 0.3445 0.847 0.036 0.140 0.000 0.824 0.000
#> GSM907865 4 0.3432 0.846 0.040 0.132 0.000 0.828 0.000
#> GSM907868 3 0.0510 0.904 0.000 0.016 0.984 0.000 0.000
#> GSM907869 3 0.4376 0.809 0.000 0.000 0.764 0.092 0.144
#> GSM907870 2 0.3935 0.671 0.000 0.760 0.012 0.220 0.008
#> GSM907861 3 0.0794 0.899 0.000 0.028 0.972 0.000 0.000
#> GSM907862 3 0.3192 0.800 0.000 0.112 0.848 0.040 0.000
#> GSM907863 3 0.3192 0.800 0.000 0.112 0.848 0.040 0.000
#> GSM907866 3 0.4194 0.830 0.000 0.004 0.788 0.080 0.128
#> GSM907867 3 0.0703 0.901 0.000 0.024 0.976 0.000 0.000
#> GSM907839 4 0.3445 0.847 0.036 0.140 0.000 0.824 0.000
#> GSM907840 4 0.3093 0.818 0.008 0.168 0.000 0.824 0.000
#> GSM907842 4 0.3093 0.818 0.008 0.168 0.000 0.824 0.000
#> GSM907843 2 0.3756 0.645 0.000 0.744 0.000 0.248 0.008
#> GSM907845 2 0.4977 0.487 0.000 0.604 0.000 0.040 0.356
#> GSM907846 2 0.4621 0.337 0.000 0.576 0.004 0.008 0.412
#> GSM907848 2 0.2069 0.801 0.000 0.912 0.000 0.012 0.076
#> GSM907851 2 0.4229 0.672 0.024 0.756 0.000 0.208 0.012
#> GSM907835 2 0.0693 0.814 0.000 0.980 0.008 0.000 0.012
#> GSM907836 2 0.1043 0.808 0.000 0.960 0.040 0.000 0.000
#> GSM907837 2 0.2077 0.798 0.000 0.920 0.040 0.040 0.000
#> GSM907838 2 0.2077 0.798 0.000 0.920 0.040 0.040 0.000
#> GSM907841 3 0.4436 0.821 0.000 0.004 0.768 0.088 0.140
#> GSM907844 2 0.1913 0.807 0.000 0.932 0.044 0.008 0.016
#> GSM907847 2 0.1082 0.812 0.000 0.964 0.000 0.008 0.028
#> GSM907849 2 0.4261 0.666 0.024 0.752 0.000 0.212 0.012
#> GSM907850 2 0.0898 0.812 0.000 0.972 0.000 0.008 0.020
#> GSM907852 2 0.0324 0.814 0.000 0.992 0.004 0.000 0.004
#> GSM907853 2 0.1557 0.810 0.000 0.940 0.000 0.008 0.052
#> GSM907807 1 0.0000 0.961 1.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.4009 0.552 0.312 0.000 0.000 0.684 0.004
#> GSM907814 4 0.4268 0.285 0.444 0.000 0.000 0.556 0.000
#> GSM907816 1 0.1197 0.952 0.952 0.000 0.000 0.000 0.048
#> GSM907818 5 0.3716 0.765 0.172 0.020 0.000 0.008 0.800
#> GSM907819 5 0.3786 0.752 0.204 0.000 0.004 0.016 0.776
#> GSM907820 5 0.4955 0.739 0.124 0.148 0.000 0.004 0.724
#> GSM907822 1 0.1197 0.952 0.952 0.000 0.000 0.000 0.048
#> GSM907823 1 0.1197 0.952 0.952 0.000 0.000 0.000 0.048
#> GSM907808 1 0.0000 0.961 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0290 0.957 0.992 0.000 0.000 0.000 0.008
#> GSM907810 1 0.0510 0.966 0.984 0.000 0.000 0.000 0.016
#> GSM907811 1 0.2230 0.866 0.884 0.000 0.000 0.000 0.116
#> GSM907812 5 0.5641 0.676 0.308 0.000 0.008 0.080 0.604
#> GSM907815 5 0.6692 0.320 0.048 0.000 0.196 0.168 0.588
#> GSM907817 5 0.4915 0.758 0.168 0.104 0.000 0.004 0.724
#> GSM907821 5 0.4593 0.754 0.128 0.124 0.000 0.000 0.748
#> GSM907824 5 0.4835 0.749 0.128 0.132 0.000 0.004 0.736
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.1410 0.85802 0.000 0.000 0.944 0.004 0.008 0.044
#> GSM907859 4 0.1036 0.84743 0.008 0.024 0.004 0.964 0.000 0.000
#> GSM907860 3 0.0363 0.85506 0.000 0.012 0.988 0.000 0.000 0.000
#> GSM907854 3 0.1410 0.85802 0.000 0.000 0.944 0.004 0.008 0.044
#> GSM907855 3 0.1245 0.85916 0.000 0.000 0.952 0.000 0.016 0.032
#> GSM907856 3 0.1245 0.85916 0.000 0.000 0.952 0.000 0.016 0.032
#> GSM907857 3 0.4232 0.73237 0.000 0.000 0.640 0.012 0.012 0.336
#> GSM907825 2 0.3720 0.74937 0.000 0.804 0.008 0.004 0.064 0.120
#> GSM907828 2 0.4861 0.66080 0.000 0.692 0.000 0.208 0.028 0.072
#> GSM907832 2 0.4063 0.76815 0.000 0.768 0.000 0.012 0.072 0.148
#> GSM907833 2 0.4026 0.77003 0.000 0.772 0.000 0.012 0.072 0.144
#> GSM907834 2 0.4222 0.71721 0.000 0.760 0.008 0.004 0.084 0.144
#> GSM907826 2 0.1168 0.80311 0.000 0.956 0.016 0.000 0.000 0.028
#> GSM907827 2 0.3665 0.75852 0.000 0.828 0.076 0.004 0.040 0.052
#> GSM907829 5 0.4572 -0.01035 0.000 0.264 0.000 0.004 0.668 0.064
#> GSM907830 4 0.5018 0.06177 0.004 0.392 0.000 0.552 0.012 0.040
#> GSM907831 2 0.4019 0.74824 0.000 0.804 0.084 0.004 0.048 0.060
#> GSM907792 1 0.0146 0.97137 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907795 1 0.0260 0.96944 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907801 1 0.0146 0.97099 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907802 5 0.6032 -0.09229 0.092 0.044 0.000 0.000 0.456 0.408
#> GSM907804 6 0.6075 -0.35907 0.192 0.000 0.000 0.008 0.400 0.400
#> GSM907805 5 0.5456 0.11354 0.440 0.004 0.000 0.000 0.452 0.104
#> GSM907806 5 0.6147 -0.13794 0.180 0.008 0.000 0.004 0.416 0.392
#> GSM907793 1 0.0405 0.96967 0.988 0.000 0.000 0.000 0.008 0.004
#> GSM907794 5 0.5750 -0.09566 0.184 0.000 0.000 0.000 0.480 0.336
#> GSM907796 5 0.2664 0.24380 0.184 0.000 0.000 0.000 0.816 0.000
#> GSM907797 5 0.4396 0.17126 0.044 0.000 0.004 0.008 0.704 0.240
#> GSM907798 5 0.2969 0.24715 0.224 0.000 0.000 0.000 0.776 0.000
#> GSM907799 1 0.0551 0.96918 0.984 0.000 0.000 0.004 0.008 0.004
#> GSM907800 5 0.6122 -0.06421 0.116 0.028 0.000 0.004 0.456 0.396
#> GSM907803 1 0.0837 0.96033 0.972 0.000 0.000 0.004 0.020 0.004
#> GSM907864 4 0.0972 0.84879 0.008 0.028 0.000 0.964 0.000 0.000
#> GSM907865 4 0.1180 0.84698 0.008 0.024 0.004 0.960 0.000 0.004
#> GSM907868 3 0.0291 0.85684 0.000 0.004 0.992 0.000 0.000 0.004
#> GSM907869 3 0.4333 0.70391 0.000 0.000 0.596 0.020 0.004 0.380
#> GSM907870 2 0.5528 0.62573 0.000 0.632 0.000 0.216 0.036 0.116
#> GSM907861 3 0.1152 0.84640 0.000 0.044 0.952 0.000 0.000 0.004
#> GSM907862 3 0.2792 0.79751 0.000 0.076 0.876 0.016 0.004 0.028
#> GSM907863 3 0.2792 0.79751 0.000 0.076 0.876 0.016 0.004 0.028
#> GSM907866 3 0.4099 0.71423 0.000 0.000 0.612 0.016 0.000 0.372
#> GSM907867 3 0.0790 0.84906 0.000 0.032 0.968 0.000 0.000 0.000
#> GSM907839 4 0.0972 0.84879 0.008 0.028 0.000 0.964 0.000 0.000
#> GSM907840 4 0.1080 0.84694 0.004 0.032 0.000 0.960 0.000 0.004
#> GSM907842 4 0.0935 0.84659 0.004 0.032 0.000 0.964 0.000 0.000
#> GSM907843 2 0.5399 0.63298 0.000 0.640 0.000 0.228 0.036 0.096
#> GSM907845 2 0.5654 0.47835 0.000 0.532 0.000 0.004 0.304 0.160
#> GSM907846 6 0.6141 0.08053 0.000 0.236 0.000 0.012 0.272 0.480
#> GSM907848 2 0.4026 0.77003 0.000 0.772 0.000 0.012 0.072 0.144
#> GSM907851 2 0.5677 0.62712 0.004 0.628 0.000 0.212 0.036 0.120
#> GSM907835 2 0.1124 0.80548 0.000 0.956 0.000 0.000 0.008 0.036
#> GSM907836 2 0.1390 0.80229 0.000 0.948 0.016 0.000 0.004 0.032
#> GSM907837 2 0.2476 0.78945 0.000 0.900 0.036 0.020 0.004 0.040
#> GSM907838 2 0.2476 0.78945 0.000 0.900 0.036 0.020 0.004 0.040
#> GSM907841 3 0.4446 0.69792 0.000 0.000 0.588 0.020 0.008 0.384
#> GSM907844 2 0.2156 0.79671 0.000 0.912 0.020 0.000 0.020 0.048
#> GSM907847 2 0.3147 0.79518 0.000 0.844 0.000 0.012 0.044 0.100
#> GSM907849 2 0.5457 0.63808 0.000 0.640 0.000 0.220 0.040 0.100
#> GSM907850 2 0.2649 0.80158 0.000 0.880 0.000 0.012 0.036 0.072
#> GSM907852 2 0.0692 0.80597 0.000 0.976 0.000 0.000 0.004 0.020
#> GSM907853 2 0.3111 0.79917 0.000 0.836 0.000 0.008 0.032 0.124
#> GSM907807 1 0.0260 0.96944 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907813 4 0.2968 0.71626 0.168 0.000 0.000 0.816 0.000 0.016
#> GSM907814 4 0.4052 0.41474 0.356 0.000 0.000 0.628 0.000 0.016
#> GSM907816 1 0.0551 0.96773 0.984 0.000 0.000 0.004 0.008 0.004
#> GSM907818 5 0.5435 -0.00948 0.120 0.004 0.000 0.000 0.544 0.332
#> GSM907819 5 0.5917 -0.11025 0.168 0.000 0.000 0.008 0.472 0.352
#> GSM907820 5 0.6039 -0.10296 0.092 0.044 0.000 0.000 0.440 0.424
#> GSM907822 1 0.0551 0.96773 0.984 0.000 0.000 0.004 0.008 0.004
#> GSM907823 1 0.1313 0.94218 0.952 0.000 0.000 0.004 0.016 0.028
#> GSM907808 1 0.0363 0.96911 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907809 1 0.0363 0.96911 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907810 1 0.0146 0.97112 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907811 1 0.2979 0.79755 0.852 0.000 0.000 0.004 0.088 0.056
#> GSM907812 5 0.3217 0.24785 0.224 0.000 0.000 0.000 0.768 0.008
#> GSM907815 5 0.5689 0.09090 0.008 0.000 0.084 0.016 0.524 0.368
#> GSM907817 5 0.6122 -0.06421 0.116 0.028 0.000 0.004 0.456 0.396
#> GSM907821 5 0.6019 -0.07763 0.092 0.044 0.000 0.000 0.472 0.392
#> GSM907824 5 0.6029 -0.07259 0.092 0.044 0.000 0.000 0.460 0.404
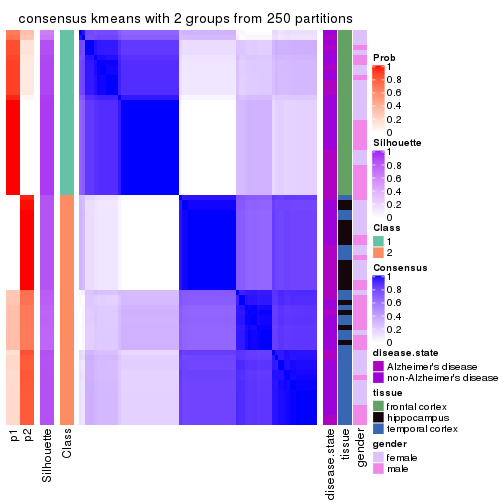
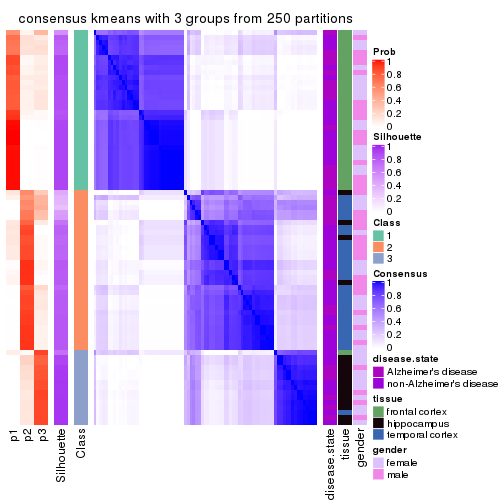
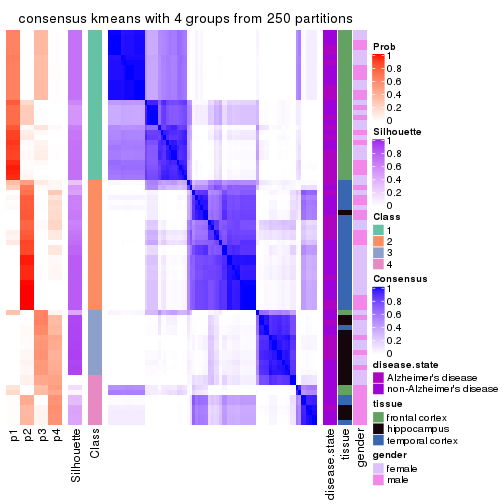
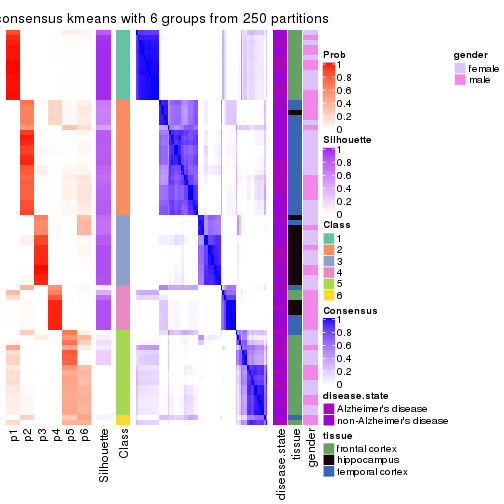
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
consensus_heatmap(res, k = 3)
consensus_heatmap(res, k = 4)
consensus_heatmap(res, k = 5)
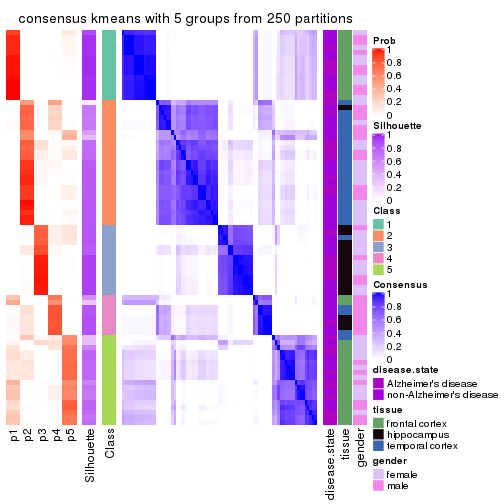
consensus_heatmap(res, k = 6)
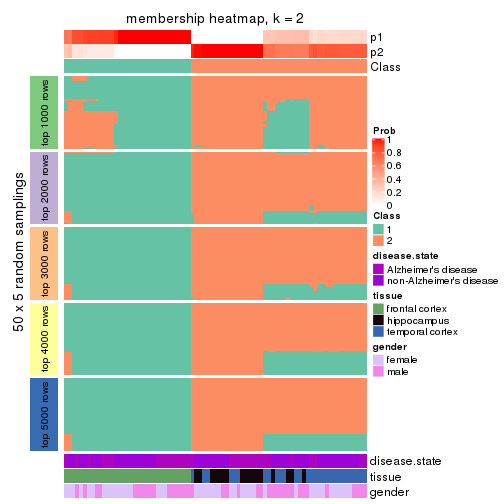
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
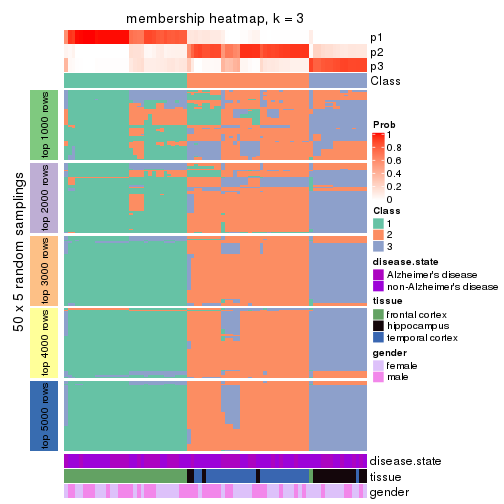
membership_heatmap(res, k = 4)
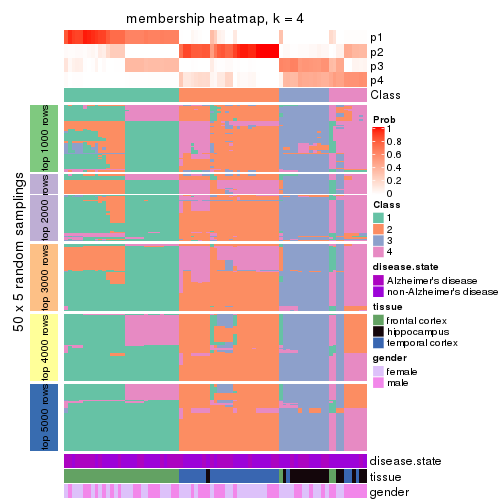
membership_heatmap(res, k = 5)
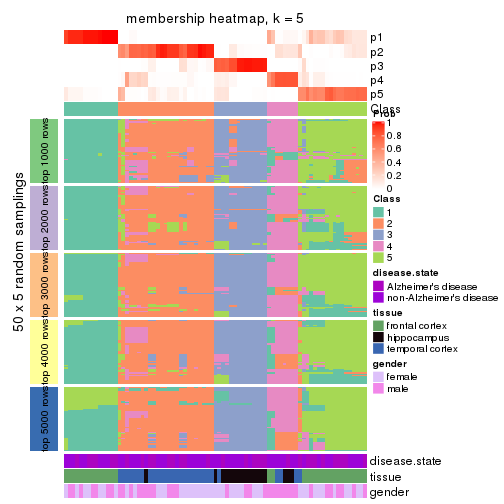
membership_heatmap(res, k = 6)
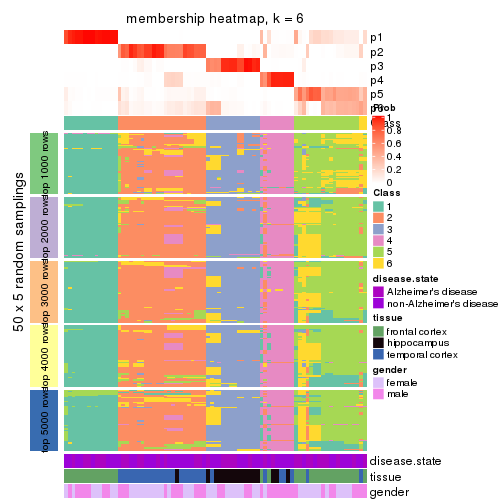
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
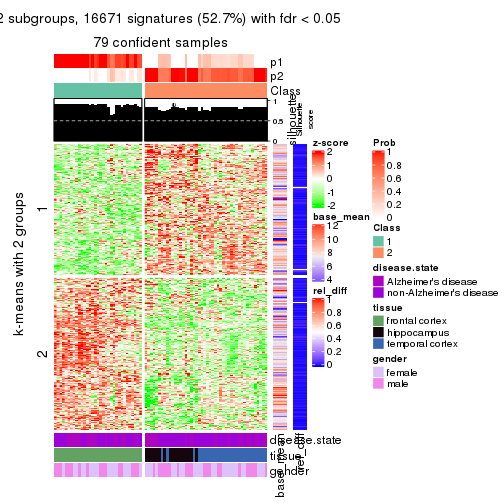
get_signatures(res, k = 3)
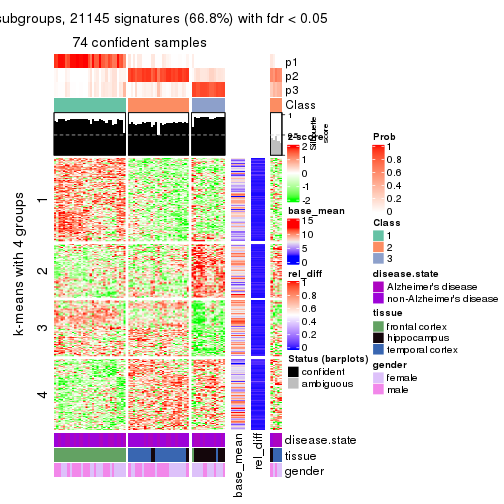
get_signatures(res, k = 4)
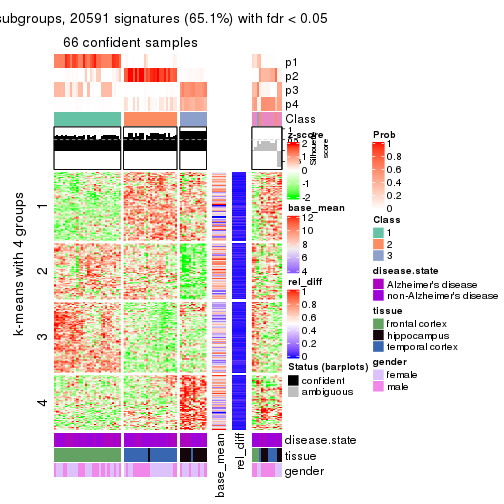
get_signatures(res, k = 5)
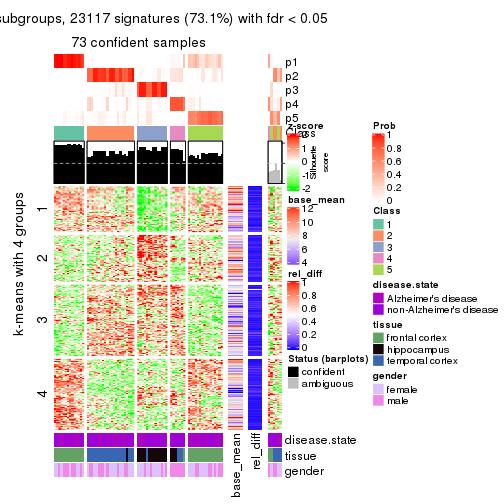
get_signatures(res, k = 6)
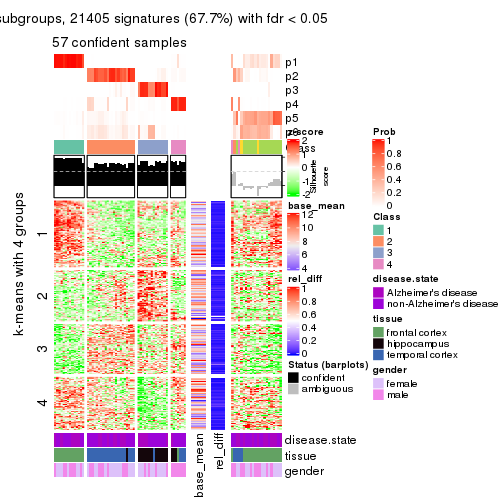
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
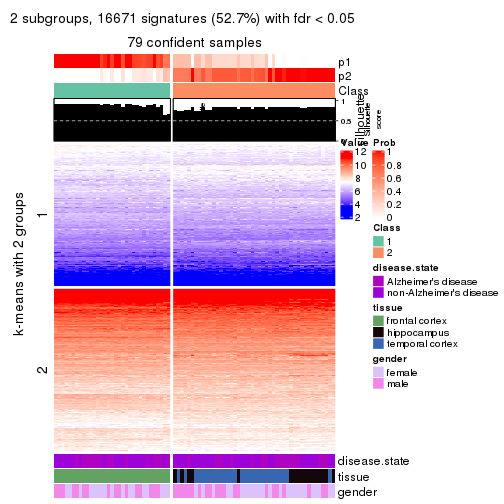
get_signatures(res, k = 3, scale_rows = FALSE)
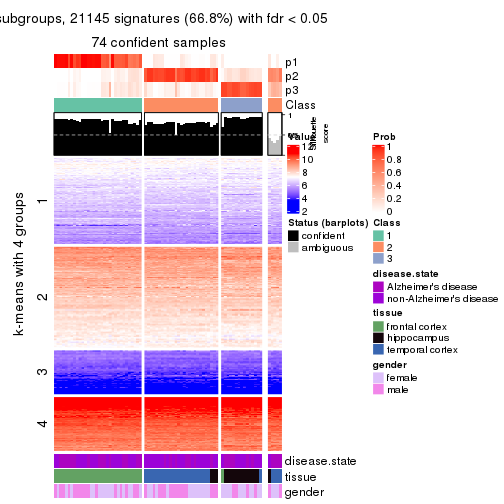
get_signatures(res, k = 4, scale_rows = FALSE)
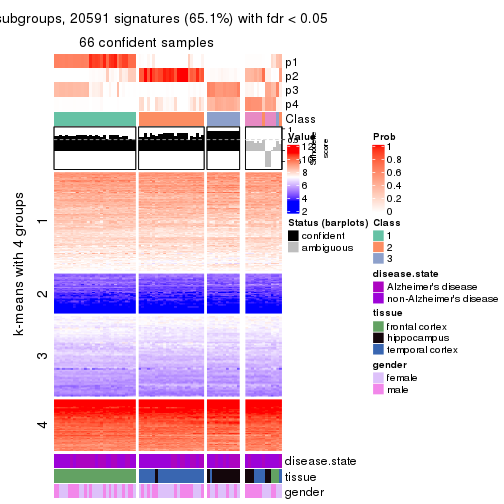
get_signatures(res, k = 5, scale_rows = FALSE)
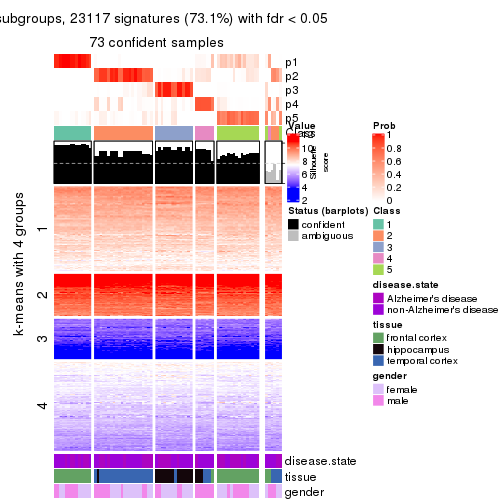
get_signatures(res, k = 6, scale_rows = FALSE)
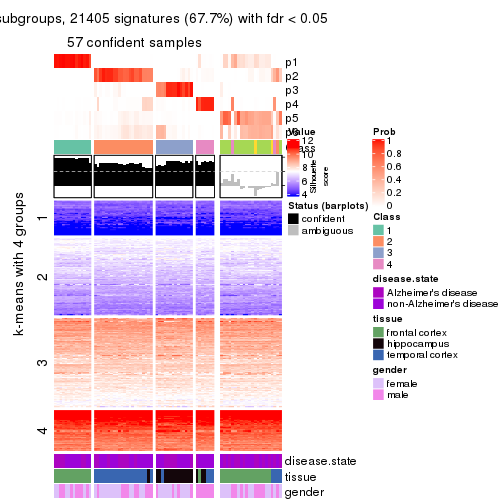
Compare the overlap of signatures from different k:
compare_signatures(res)
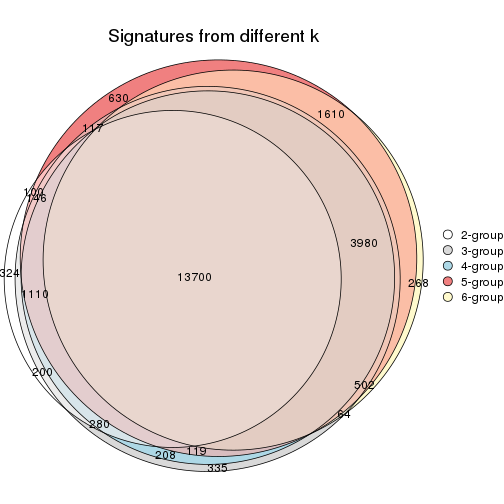
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
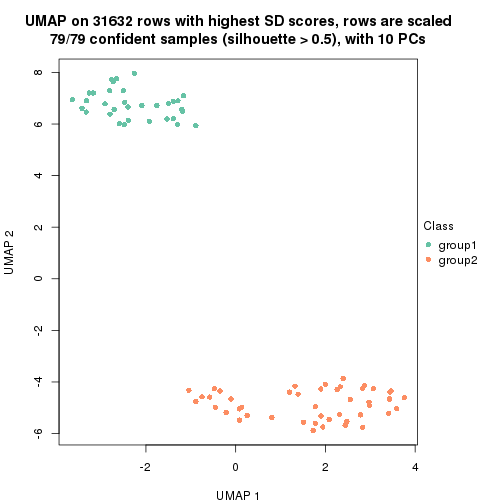
dimension_reduction(res, k = 3, method = "UMAP")
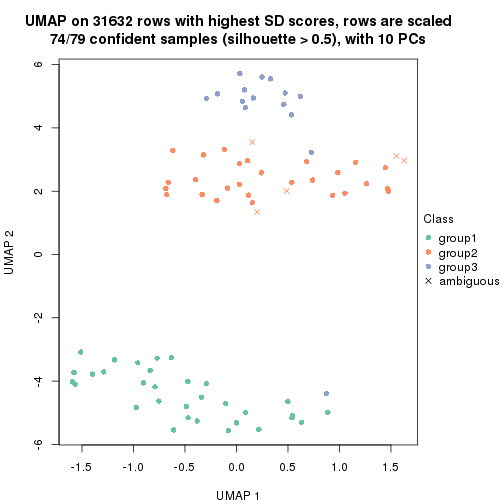
dimension_reduction(res, k = 4, method = "UMAP")
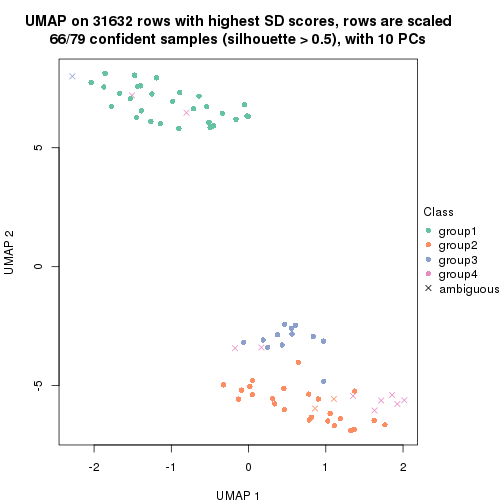
dimension_reduction(res, k = 5, method = "UMAP")
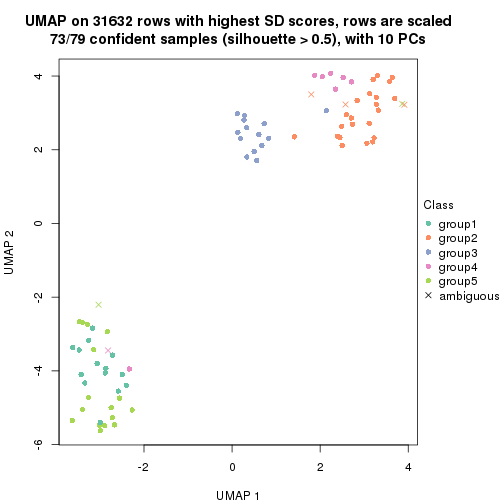
dimension_reduction(res, k = 6, method = "UMAP")
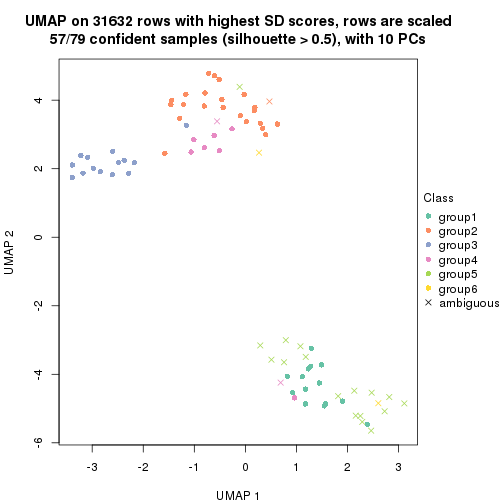
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
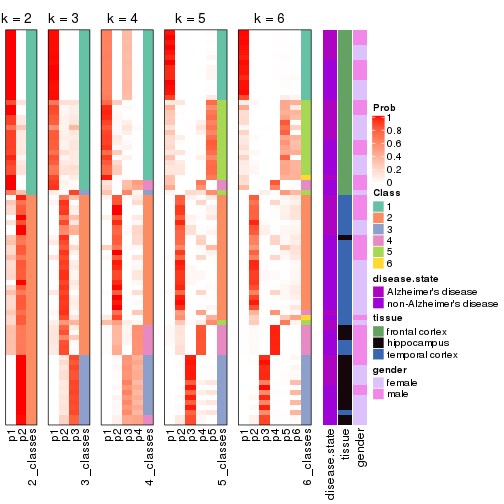
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:kmeans 79 0.599 7.00e-18 0.9838 2
#> SD:kmeans 74 0.250 6.55e-24 0.1833 3
#> SD:kmeans 66 0.423 2.94e-24 0.7141 4
#> SD:kmeans 73 0.429 8.46e-22 0.0364 5
#> SD:kmeans 57 0.579 2.41e-17 0.0172 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "skmeans"]
# you can also extract it by
# res = res_list["SD:skmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
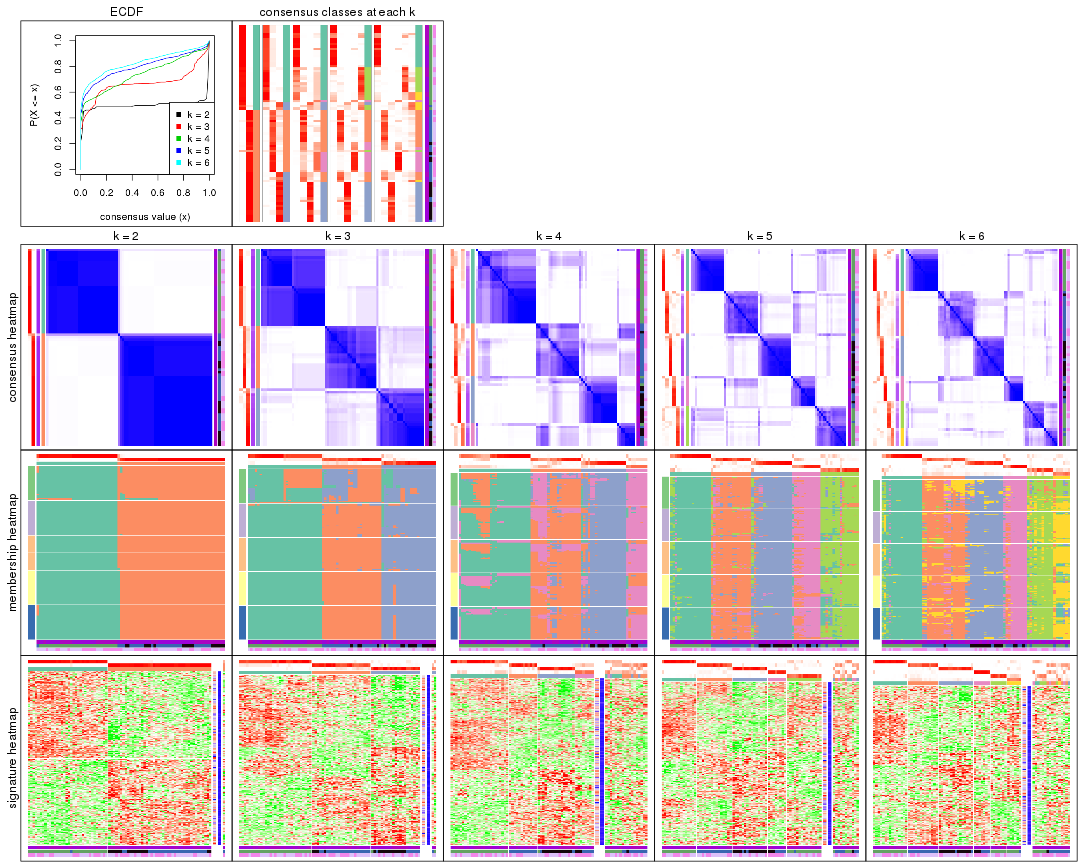
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
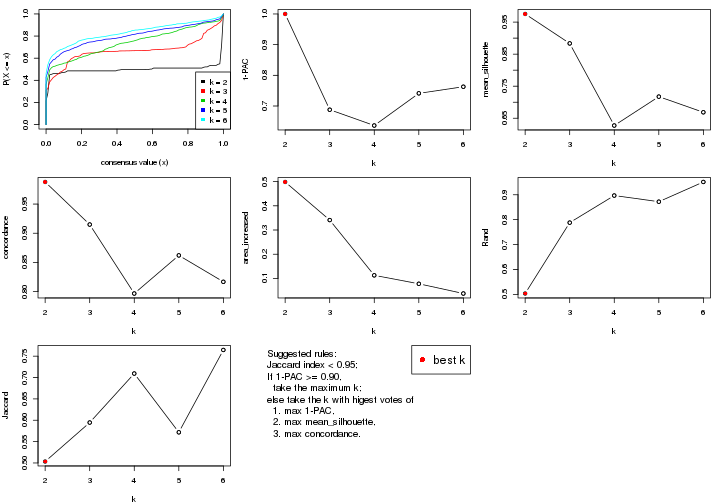
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.975 0.988 0.4984 0.503 0.503
#> 3 3 0.688 0.883 0.915 0.3411 0.788 0.595
#> 4 4 0.636 0.627 0.797 0.1127 0.897 0.709
#> 5 5 0.741 0.717 0.862 0.0779 0.872 0.572
#> 6 6 0.763 0.669 0.817 0.0377 0.951 0.765
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.985 0.000 1.000
#> GSM907859 2 0.0938 0.981 0.012 0.988
#> GSM907860 2 0.0000 0.985 0.000 1.000
#> GSM907854 2 0.0000 0.985 0.000 1.000
#> GSM907855 2 0.0000 0.985 0.000 1.000
#> GSM907856 2 0.0000 0.985 0.000 1.000
#> GSM907857 2 0.0000 0.985 0.000 1.000
#> GSM907825 2 0.0000 0.985 0.000 1.000
#> GSM907828 2 0.0938 0.981 0.012 0.988
#> GSM907832 2 0.0000 0.985 0.000 1.000
#> GSM907833 2 0.0000 0.985 0.000 1.000
#> GSM907834 2 0.0000 0.985 0.000 1.000
#> GSM907826 2 0.0000 0.985 0.000 1.000
#> GSM907827 2 0.0000 0.985 0.000 1.000
#> GSM907829 1 0.5294 0.874 0.880 0.120
#> GSM907830 2 0.0938 0.981 0.012 0.988
#> GSM907831 2 0.0000 0.985 0.000 1.000
#> GSM907792 1 0.0000 0.992 1.000 0.000
#> GSM907795 1 0.0000 0.992 1.000 0.000
#> GSM907801 1 0.0000 0.992 1.000 0.000
#> GSM907802 1 0.0938 0.989 0.988 0.012
#> GSM907804 1 0.0000 0.992 1.000 0.000
#> GSM907805 1 0.0000 0.992 1.000 0.000
#> GSM907806 1 0.0000 0.992 1.000 0.000
#> GSM907793 1 0.0000 0.992 1.000 0.000
#> GSM907794 1 0.0938 0.989 0.988 0.012
#> GSM907796 1 0.0938 0.989 0.988 0.012
#> GSM907797 1 0.0938 0.989 0.988 0.012
#> GSM907798 1 0.0938 0.989 0.988 0.012
#> GSM907799 1 0.0000 0.992 1.000 0.000
#> GSM907800 1 0.0672 0.991 0.992 0.008
#> GSM907803 1 0.0000 0.992 1.000 0.000
#> GSM907864 2 0.0938 0.981 0.012 0.988
#> GSM907865 2 0.0938 0.981 0.012 0.988
#> GSM907868 2 0.0000 0.985 0.000 1.000
#> GSM907869 2 0.0000 0.985 0.000 1.000
#> GSM907870 2 0.0938 0.981 0.012 0.988
#> GSM907861 2 0.0000 0.985 0.000 1.000
#> GSM907862 2 0.0672 0.982 0.008 0.992
#> GSM907863 2 0.0672 0.982 0.008 0.992
#> GSM907866 2 0.0000 0.985 0.000 1.000
#> GSM907867 2 0.0000 0.985 0.000 1.000
#> GSM907839 2 0.0938 0.981 0.012 0.988
#> GSM907840 2 0.0938 0.981 0.012 0.988
#> GSM907842 2 0.0938 0.981 0.012 0.988
#> GSM907843 2 0.0938 0.981 0.012 0.988
#> GSM907845 2 0.0000 0.985 0.000 1.000
#> GSM907846 2 0.9732 0.310 0.404 0.596
#> GSM907848 2 0.0000 0.985 0.000 1.000
#> GSM907851 2 0.4161 0.912 0.084 0.916
#> GSM907835 2 0.0000 0.985 0.000 1.000
#> GSM907836 2 0.0000 0.985 0.000 1.000
#> GSM907837 2 0.0938 0.981 0.012 0.988
#> GSM907838 2 0.0938 0.981 0.012 0.988
#> GSM907841 2 0.0000 0.985 0.000 1.000
#> GSM907844 2 0.0000 0.985 0.000 1.000
#> GSM907847 2 0.0000 0.985 0.000 1.000
#> GSM907849 2 0.2236 0.962 0.036 0.964
#> GSM907850 2 0.0000 0.985 0.000 1.000
#> GSM907852 2 0.0000 0.985 0.000 1.000
#> GSM907853 2 0.0000 0.985 0.000 1.000
#> GSM907807 1 0.0000 0.992 1.000 0.000
#> GSM907813 1 0.0000 0.992 1.000 0.000
#> GSM907814 1 0.0000 0.992 1.000 0.000
#> GSM907816 1 0.0000 0.992 1.000 0.000
#> GSM907818 1 0.0938 0.989 0.988 0.012
#> GSM907819 1 0.0938 0.989 0.988 0.012
#> GSM907820 1 0.0672 0.991 0.992 0.008
#> GSM907822 1 0.0000 0.992 1.000 0.000
#> GSM907823 1 0.0000 0.992 1.000 0.000
#> GSM907808 1 0.0000 0.992 1.000 0.000
#> GSM907809 1 0.0000 0.992 1.000 0.000
#> GSM907810 1 0.0000 0.992 1.000 0.000
#> GSM907811 1 0.0000 0.992 1.000 0.000
#> GSM907812 1 0.0672 0.991 0.992 0.008
#> GSM907815 1 0.0938 0.989 0.988 0.012
#> GSM907817 1 0.0672 0.991 0.992 0.008
#> GSM907821 1 0.0938 0.989 0.988 0.012
#> GSM907824 1 0.0938 0.989 0.988 0.012
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907859 2 0.1964 0.865 0.000 0.944 0.056
#> GSM907860 3 0.1411 0.901 0.000 0.036 0.964
#> GSM907854 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907855 3 0.1411 0.901 0.000 0.036 0.964
#> GSM907856 3 0.1411 0.901 0.000 0.036 0.964
#> GSM907857 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907825 3 0.2492 0.889 0.016 0.048 0.936
#> GSM907828 2 0.1753 0.891 0.000 0.952 0.048
#> GSM907832 2 0.5200 0.852 0.020 0.796 0.184
#> GSM907833 2 0.4679 0.876 0.020 0.832 0.148
#> GSM907834 3 0.2414 0.892 0.020 0.040 0.940
#> GSM907826 2 0.5363 0.761 0.000 0.724 0.276
#> GSM907827 3 0.0747 0.912 0.000 0.016 0.984
#> GSM907829 3 0.4209 0.844 0.120 0.020 0.860
#> GSM907830 2 0.0747 0.879 0.000 0.984 0.016
#> GSM907831 3 0.1163 0.903 0.000 0.028 0.972
#> GSM907792 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907795 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907801 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907802 1 0.3183 0.857 0.908 0.016 0.076
#> GSM907804 1 0.1163 0.931 0.972 0.028 0.000
#> GSM907805 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907806 1 0.0237 0.927 0.996 0.004 0.000
#> GSM907793 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907794 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907797 3 0.6154 0.428 0.408 0.000 0.592
#> GSM907798 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907799 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907800 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907803 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907864 2 0.0892 0.879 0.000 0.980 0.020
#> GSM907865 2 0.1753 0.869 0.000 0.952 0.048
#> GSM907868 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907869 3 0.2165 0.883 0.064 0.000 0.936
#> GSM907870 2 0.2356 0.891 0.000 0.928 0.072
#> GSM907861 3 0.0237 0.912 0.000 0.004 0.996
#> GSM907862 3 0.2796 0.862 0.000 0.092 0.908
#> GSM907863 3 0.2796 0.862 0.000 0.092 0.908
#> GSM907866 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907867 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907839 2 0.0892 0.879 0.000 0.980 0.020
#> GSM907840 2 0.0892 0.879 0.000 0.980 0.020
#> GSM907842 2 0.0892 0.879 0.000 0.980 0.020
#> GSM907843 2 0.0000 0.880 0.000 1.000 0.000
#> GSM907845 3 0.4786 0.842 0.112 0.044 0.844
#> GSM907846 2 0.7082 0.773 0.120 0.724 0.156
#> GSM907848 2 0.4551 0.879 0.020 0.840 0.140
#> GSM907851 2 0.0000 0.880 0.000 1.000 0.000
#> GSM907835 2 0.4452 0.858 0.000 0.808 0.192
#> GSM907836 2 0.4504 0.855 0.000 0.804 0.196
#> GSM907837 2 0.3192 0.883 0.000 0.888 0.112
#> GSM907838 2 0.3192 0.883 0.000 0.888 0.112
#> GSM907841 3 0.0000 0.913 0.000 0.000 1.000
#> GSM907844 3 0.5835 0.362 0.000 0.340 0.660
#> GSM907847 2 0.4418 0.881 0.020 0.848 0.132
#> GSM907849 2 0.0000 0.880 0.000 1.000 0.000
#> GSM907850 2 0.4002 0.876 0.000 0.840 0.160
#> GSM907852 2 0.4452 0.858 0.000 0.808 0.192
#> GSM907853 2 0.4982 0.873 0.036 0.828 0.136
#> GSM907807 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907813 1 0.4452 0.872 0.808 0.192 0.000
#> GSM907814 1 0.3412 0.928 0.876 0.124 0.000
#> GSM907816 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907818 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907820 1 0.0747 0.919 0.984 0.016 0.000
#> GSM907822 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907823 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907808 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907809 1 0.2959 0.936 0.900 0.100 0.000
#> GSM907810 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907811 1 0.3192 0.935 0.888 0.112 0.000
#> GSM907812 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907815 3 0.3686 0.831 0.140 0.000 0.860
#> GSM907817 1 0.0000 0.926 1.000 0.000 0.000
#> GSM907821 1 0.3272 0.853 0.904 0.016 0.080
#> GSM907824 1 0.2152 0.894 0.948 0.016 0.036
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907859 4 0.5499 0.8022 0.008 0.196 0.064 0.732
#> GSM907860 3 0.0592 0.8570 0.000 0.000 0.984 0.016
#> GSM907854 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907855 3 0.0592 0.8570 0.000 0.000 0.984 0.016
#> GSM907856 3 0.0592 0.8570 0.000 0.000 0.984 0.016
#> GSM907857 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907825 2 0.5847 0.3433 0.000 0.628 0.320 0.052
#> GSM907828 2 0.5119 -0.2098 0.000 0.556 0.004 0.440
#> GSM907832 2 0.1004 0.6668 0.000 0.972 0.024 0.004
#> GSM907833 2 0.0672 0.6635 0.000 0.984 0.008 0.008
#> GSM907834 2 0.5639 0.3509 0.000 0.636 0.324 0.040
#> GSM907826 2 0.3266 0.6162 0.000 0.832 0.168 0.000
#> GSM907827 3 0.2796 0.7947 0.000 0.092 0.892 0.016
#> GSM907829 3 0.7963 0.2182 0.012 0.284 0.472 0.232
#> GSM907830 4 0.4372 0.8408 0.000 0.268 0.004 0.728
#> GSM907831 3 0.4898 0.2238 0.000 0.416 0.584 0.000
#> GSM907792 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907802 1 0.7840 0.3888 0.392 0.340 0.000 0.268
#> GSM907804 1 0.2973 0.7859 0.856 0.000 0.000 0.144
#> GSM907805 1 0.2888 0.7885 0.872 0.004 0.000 0.124
#> GSM907806 1 0.2271 0.7953 0.916 0.008 0.000 0.076
#> GSM907793 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907794 1 0.4134 0.7521 0.740 0.000 0.000 0.260
#> GSM907796 1 0.4976 0.7417 0.716 0.004 0.020 0.260
#> GSM907797 3 0.8217 -0.0251 0.328 0.016 0.416 0.240
#> GSM907798 1 0.4535 0.7526 0.744 0.000 0.016 0.240
#> GSM907799 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907800 1 0.6189 0.6976 0.640 0.092 0.000 0.268
#> GSM907803 1 0.0188 0.7990 0.996 0.000 0.000 0.004
#> GSM907864 4 0.4601 0.8462 0.008 0.256 0.004 0.732
#> GSM907865 4 0.5516 0.8086 0.012 0.200 0.056 0.732
#> GSM907868 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907869 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907870 2 0.5143 -0.2616 0.000 0.540 0.004 0.456
#> GSM907861 3 0.0336 0.8602 0.000 0.008 0.992 0.000
#> GSM907862 3 0.3324 0.7516 0.000 0.012 0.852 0.136
#> GSM907863 3 0.3271 0.7557 0.000 0.012 0.856 0.132
#> GSM907866 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907867 3 0.0779 0.8579 0.000 0.004 0.980 0.016
#> GSM907839 4 0.4601 0.8462 0.008 0.256 0.004 0.732
#> GSM907840 4 0.4343 0.8442 0.000 0.264 0.004 0.732
#> GSM907842 4 0.4343 0.8442 0.000 0.264 0.004 0.732
#> GSM907843 4 0.5060 0.5796 0.000 0.412 0.004 0.584
#> GSM907845 2 0.5913 0.5059 0.000 0.696 0.124 0.180
#> GSM907846 2 0.8304 0.2414 0.036 0.440 0.172 0.352
#> GSM907848 2 0.0376 0.6625 0.000 0.992 0.004 0.004
#> GSM907851 2 0.5558 -0.2299 0.020 0.548 0.000 0.432
#> GSM907835 2 0.0817 0.6663 0.000 0.976 0.024 0.000
#> GSM907836 2 0.4513 0.5856 0.000 0.804 0.120 0.076
#> GSM907837 2 0.3831 0.4639 0.000 0.792 0.004 0.204
#> GSM907838 2 0.4194 0.4200 0.000 0.764 0.008 0.228
#> GSM907841 3 0.0188 0.8615 0.000 0.004 0.996 0.000
#> GSM907844 2 0.3975 0.5650 0.000 0.760 0.240 0.000
#> GSM907847 2 0.0817 0.6547 0.000 0.976 0.000 0.024
#> GSM907849 2 0.5161 -0.3295 0.000 0.520 0.004 0.476
#> GSM907850 2 0.1356 0.6552 0.000 0.960 0.008 0.032
#> GSM907852 2 0.0707 0.6666 0.000 0.980 0.020 0.000
#> GSM907853 2 0.0672 0.6640 0.000 0.984 0.008 0.008
#> GSM907807 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907813 4 0.4679 0.4415 0.352 0.000 0.000 0.648
#> GSM907814 1 0.4998 -0.1203 0.512 0.000 0.000 0.488
#> GSM907816 1 0.0592 0.7917 0.984 0.000 0.000 0.016
#> GSM907818 1 0.7305 0.6284 0.560 0.164 0.008 0.268
#> GSM907819 1 0.4797 0.7440 0.720 0.000 0.020 0.260
#> GSM907820 1 0.7851 0.3560 0.376 0.356 0.000 0.268
#> GSM907822 1 0.0592 0.7914 0.984 0.000 0.000 0.016
#> GSM907823 1 0.0707 0.7892 0.980 0.000 0.000 0.020
#> GSM907808 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.7990 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0336 0.7989 0.992 0.000 0.000 0.008
#> GSM907812 1 0.4053 0.7606 0.768 0.000 0.004 0.228
#> GSM907815 3 0.4214 0.6831 0.016 0.000 0.780 0.204
#> GSM907817 1 0.7344 0.5859 0.524 0.208 0.000 0.268
#> GSM907821 1 0.7974 0.4196 0.408 0.320 0.004 0.268
#> GSM907824 1 0.7843 0.3810 0.388 0.344 0.000 0.268
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0162 0.8945 0.000 0.004 0.996 0.000 0.000
#> GSM907859 4 0.1012 0.7832 0.000 0.020 0.012 0.968 0.000
#> GSM907860 3 0.0162 0.8941 0.000 0.004 0.996 0.000 0.000
#> GSM907854 3 0.0162 0.8945 0.000 0.004 0.996 0.000 0.000
#> GSM907855 3 0.0000 0.8946 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 0.8946 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0693 0.8891 0.000 0.012 0.980 0.000 0.008
#> GSM907825 2 0.4617 0.6689 0.000 0.736 0.196 0.004 0.064
#> GSM907828 4 0.4101 0.4478 0.000 0.372 0.000 0.628 0.000
#> GSM907832 2 0.2618 0.8177 0.000 0.900 0.012 0.052 0.036
#> GSM907833 2 0.2300 0.8145 0.000 0.904 0.000 0.072 0.024
#> GSM907834 2 0.4370 0.7015 0.000 0.764 0.168 0.004 0.064
#> GSM907826 2 0.1894 0.8086 0.000 0.920 0.072 0.008 0.000
#> GSM907827 3 0.3086 0.7389 0.000 0.180 0.816 0.004 0.000
#> GSM907829 5 0.6725 0.5648 0.028 0.148 0.184 0.024 0.616
#> GSM907830 4 0.1270 0.7834 0.000 0.052 0.000 0.948 0.000
#> GSM907831 3 0.4888 -0.0177 0.000 0.472 0.508 0.004 0.016
#> GSM907792 1 0.0162 0.9060 0.996 0.000 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0162 0.9064 0.996 0.000 0.000 0.000 0.004
#> GSM907802 5 0.1670 0.7923 0.012 0.052 0.000 0.000 0.936
#> GSM907804 5 0.4251 0.5100 0.316 0.000 0.000 0.012 0.672
#> GSM907805 1 0.4607 0.2727 0.620 0.008 0.000 0.008 0.364
#> GSM907806 1 0.4415 0.1127 0.552 0.004 0.000 0.000 0.444
#> GSM907793 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.3366 0.6927 0.232 0.000 0.000 0.000 0.768
#> GSM907796 5 0.4042 0.7172 0.196 0.012 0.000 0.020 0.772
#> GSM907797 5 0.5631 0.6693 0.088 0.012 0.172 0.024 0.704
#> GSM907798 5 0.4607 0.6367 0.276 0.012 0.000 0.020 0.692
#> GSM907799 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.1836 0.7962 0.036 0.032 0.000 0.000 0.932
#> GSM907803 1 0.1197 0.8770 0.952 0.000 0.000 0.000 0.048
#> GSM907864 4 0.0880 0.7903 0.000 0.032 0.000 0.968 0.000
#> GSM907865 4 0.1012 0.7832 0.000 0.020 0.012 0.968 0.000
#> GSM907868 3 0.0000 0.8946 0.000 0.000 1.000 0.000 0.000
#> GSM907869 3 0.1507 0.8733 0.000 0.012 0.952 0.012 0.024
#> GSM907870 4 0.4583 0.2108 0.000 0.464 0.004 0.528 0.004
#> GSM907861 3 0.0510 0.8923 0.000 0.016 0.984 0.000 0.000
#> GSM907862 3 0.2632 0.8271 0.000 0.040 0.888 0.072 0.000
#> GSM907863 3 0.2770 0.8205 0.000 0.044 0.880 0.076 0.000
#> GSM907866 3 0.0486 0.8936 0.000 0.004 0.988 0.004 0.004
#> GSM907867 3 0.0404 0.8920 0.000 0.012 0.988 0.000 0.000
#> GSM907839 4 0.0880 0.7903 0.000 0.032 0.000 0.968 0.000
#> GSM907840 4 0.0794 0.7895 0.000 0.028 0.000 0.972 0.000
#> GSM907842 4 0.0880 0.7903 0.000 0.032 0.000 0.968 0.000
#> GSM907843 4 0.3395 0.6489 0.000 0.236 0.000 0.764 0.000
#> GSM907845 2 0.5602 0.4494 0.000 0.620 0.052 0.024 0.304
#> GSM907846 5 0.8604 0.1999 0.024 0.228 0.124 0.220 0.404
#> GSM907848 2 0.1965 0.8196 0.000 0.924 0.000 0.052 0.024
#> GSM907851 2 0.5493 -0.1888 0.052 0.488 0.000 0.456 0.004
#> GSM907835 2 0.0566 0.8220 0.000 0.984 0.012 0.000 0.004
#> GSM907836 2 0.2359 0.8054 0.000 0.904 0.060 0.036 0.000
#> GSM907837 2 0.2625 0.7700 0.000 0.876 0.016 0.108 0.000
#> GSM907838 2 0.3098 0.7284 0.000 0.836 0.016 0.148 0.000
#> GSM907841 3 0.0613 0.8924 0.000 0.004 0.984 0.008 0.004
#> GSM907844 2 0.3001 0.7540 0.000 0.844 0.144 0.008 0.004
#> GSM907847 2 0.2069 0.8101 0.000 0.912 0.000 0.076 0.012
#> GSM907849 4 0.4744 0.3654 0.020 0.408 0.000 0.572 0.000
#> GSM907850 2 0.1478 0.8152 0.000 0.936 0.000 0.064 0.000
#> GSM907852 2 0.0854 0.8217 0.000 0.976 0.012 0.004 0.008
#> GSM907853 2 0.1579 0.8223 0.000 0.944 0.000 0.032 0.024
#> GSM907807 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.4249 0.0901 0.432 0.000 0.000 0.568 0.000
#> GSM907814 1 0.3366 0.6698 0.768 0.000 0.000 0.232 0.000
#> GSM907816 1 0.0290 0.9050 0.992 0.000 0.000 0.000 0.008
#> GSM907818 5 0.1018 0.7940 0.016 0.016 0.000 0.000 0.968
#> GSM907819 5 0.2339 0.7750 0.100 0.004 0.000 0.004 0.892
#> GSM907820 5 0.2753 0.7352 0.008 0.136 0.000 0.000 0.856
#> GSM907822 1 0.0451 0.9039 0.988 0.000 0.000 0.004 0.008
#> GSM907823 1 0.0404 0.9038 0.988 0.000 0.000 0.000 0.012
#> GSM907808 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0162 0.9052 0.996 0.000 0.000 0.000 0.004
#> GSM907810 1 0.0000 0.9070 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2329 0.8044 0.876 0.000 0.000 0.000 0.124
#> GSM907812 5 0.4846 0.5642 0.324 0.012 0.000 0.020 0.644
#> GSM907815 3 0.6129 -0.1386 0.036 0.012 0.464 0.028 0.460
#> GSM907817 5 0.1648 0.7962 0.020 0.040 0.000 0.000 0.940
#> GSM907821 5 0.1168 0.7942 0.008 0.032 0.000 0.000 0.960
#> GSM907824 5 0.1502 0.7892 0.004 0.056 0.000 0.000 0.940
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0937 0.8791 0.000 0.000 0.960 0.000 0.000 0.040
#> GSM907859 4 0.0260 0.8207 0.000 0.000 0.008 0.992 0.000 0.000
#> GSM907860 3 0.0964 0.8784 0.000 0.012 0.968 0.004 0.000 0.016
#> GSM907854 3 0.0632 0.8815 0.000 0.000 0.976 0.000 0.000 0.024
#> GSM907855 3 0.0458 0.8830 0.000 0.000 0.984 0.000 0.000 0.016
#> GSM907856 3 0.0458 0.8830 0.000 0.000 0.984 0.000 0.000 0.016
#> GSM907857 3 0.1663 0.8615 0.000 0.000 0.912 0.000 0.000 0.088
#> GSM907825 2 0.6543 0.4908 0.000 0.540 0.188 0.000 0.088 0.184
#> GSM907828 4 0.4701 -0.0500 0.000 0.480 0.008 0.484 0.000 0.028
#> GSM907832 2 0.4894 0.7073 0.000 0.688 0.000 0.020 0.092 0.200
#> GSM907833 2 0.4778 0.7130 0.000 0.704 0.000 0.028 0.072 0.196
#> GSM907834 2 0.6958 0.4875 0.000 0.488 0.172 0.000 0.132 0.208
#> GSM907826 2 0.2186 0.7162 0.000 0.908 0.048 0.000 0.008 0.036
#> GSM907827 3 0.4553 0.6574 0.000 0.168 0.720 0.004 0.004 0.104
#> GSM907829 6 0.4640 0.6173 0.008 0.032 0.088 0.000 0.120 0.752
#> GSM907830 4 0.0692 0.8154 0.000 0.004 0.000 0.976 0.000 0.020
#> GSM907831 3 0.6044 0.0322 0.000 0.384 0.468 0.000 0.032 0.116
#> GSM907792 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.1321 0.7212 0.004 0.020 0.000 0.000 0.952 0.024
#> GSM907804 5 0.3822 0.6121 0.180 0.000 0.000 0.016 0.772 0.032
#> GSM907805 1 0.5758 -0.2095 0.456 0.000 0.000 0.000 0.176 0.368
#> GSM907806 1 0.4705 -0.0610 0.480 0.000 0.000 0.000 0.476 0.044
#> GSM907793 1 0.0260 0.8824 0.992 0.000 0.000 0.000 0.000 0.008
#> GSM907794 5 0.4931 0.4734 0.216 0.000 0.000 0.000 0.648 0.136
#> GSM907796 6 0.5046 0.5919 0.112 0.000 0.000 0.000 0.280 0.608
#> GSM907797 6 0.4886 0.6249 0.012 0.000 0.088 0.000 0.232 0.668
#> GSM907798 6 0.5187 0.6121 0.148 0.000 0.000 0.000 0.244 0.608
#> GSM907799 1 0.0146 0.8857 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907800 5 0.1845 0.7220 0.028 0.000 0.000 0.000 0.920 0.052
#> GSM907803 1 0.0937 0.8631 0.960 0.000 0.000 0.000 0.040 0.000
#> GSM907864 4 0.0146 0.8263 0.000 0.004 0.000 0.996 0.000 0.000
#> GSM907865 4 0.0000 0.8248 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.0865 0.8826 0.000 0.000 0.964 0.000 0.000 0.036
#> GSM907869 3 0.2558 0.8003 0.000 0.000 0.840 0.004 0.000 0.156
#> GSM907870 2 0.4989 0.2801 0.000 0.568 0.004 0.360 0.000 0.068
#> GSM907861 3 0.1245 0.8800 0.000 0.016 0.952 0.000 0.000 0.032
#> GSM907862 3 0.2965 0.8248 0.000 0.076 0.864 0.024 0.000 0.036
#> GSM907863 3 0.3140 0.8107 0.000 0.096 0.848 0.020 0.000 0.036
#> GSM907866 3 0.1531 0.8704 0.000 0.000 0.928 0.004 0.000 0.068
#> GSM907867 3 0.1232 0.8741 0.000 0.016 0.956 0.004 0.000 0.024
#> GSM907839 4 0.0146 0.8263 0.000 0.004 0.000 0.996 0.000 0.000
#> GSM907840 4 0.0146 0.8263 0.000 0.004 0.000 0.996 0.000 0.000
#> GSM907842 4 0.0146 0.8263 0.000 0.004 0.000 0.996 0.000 0.000
#> GSM907843 4 0.4794 0.3116 0.000 0.328 0.000 0.608 0.004 0.060
#> GSM907845 6 0.4465 0.2997 0.000 0.212 0.004 0.000 0.080 0.704
#> GSM907846 5 0.8203 0.2551 0.016 0.136 0.072 0.124 0.448 0.204
#> GSM907848 2 0.4601 0.7138 0.000 0.708 0.000 0.016 0.072 0.204
#> GSM907851 2 0.6050 0.3799 0.060 0.572 0.000 0.272 0.004 0.092
#> GSM907835 2 0.2020 0.7396 0.000 0.896 0.000 0.000 0.008 0.096
#> GSM907836 2 0.2220 0.7152 0.000 0.908 0.044 0.012 0.000 0.036
#> GSM907837 2 0.2861 0.6980 0.000 0.880 0.020 0.048 0.008 0.044
#> GSM907838 2 0.3108 0.6826 0.000 0.860 0.020 0.072 0.004 0.044
#> GSM907841 3 0.1644 0.8684 0.000 0.000 0.920 0.004 0.000 0.076
#> GSM907844 2 0.4892 0.6114 0.000 0.696 0.176 0.000 0.020 0.108
#> GSM907847 2 0.4399 0.7201 0.000 0.736 0.000 0.036 0.040 0.188
#> GSM907849 2 0.5768 0.0877 0.020 0.472 0.000 0.416 0.004 0.088
#> GSM907850 2 0.2915 0.7328 0.000 0.848 0.000 0.024 0.008 0.120
#> GSM907852 2 0.1341 0.7314 0.000 0.948 0.000 0.000 0.024 0.028
#> GSM907853 2 0.4099 0.7261 0.000 0.748 0.000 0.020 0.036 0.196
#> GSM907807 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.3634 0.3415 0.356 0.000 0.000 0.644 0.000 0.000
#> GSM907814 1 0.3221 0.5966 0.736 0.000 0.000 0.264 0.000 0.000
#> GSM907816 1 0.0405 0.8832 0.988 0.000 0.000 0.000 0.008 0.004
#> GSM907818 5 0.3636 0.3626 0.004 0.000 0.000 0.000 0.676 0.320
#> GSM907819 5 0.4580 0.3228 0.052 0.000 0.000 0.000 0.612 0.336
#> GSM907820 5 0.1777 0.6909 0.004 0.024 0.000 0.000 0.928 0.044
#> GSM907822 1 0.0260 0.8848 0.992 0.000 0.000 0.000 0.000 0.008
#> GSM907823 1 0.0363 0.8828 0.988 0.000 0.000 0.000 0.000 0.012
#> GSM907808 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.8868 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2902 0.6962 0.800 0.000 0.000 0.000 0.196 0.004
#> GSM907812 6 0.5275 0.6038 0.168 0.000 0.000 0.000 0.232 0.600
#> GSM907815 6 0.4830 0.5531 0.008 0.000 0.216 0.004 0.088 0.684
#> GSM907817 5 0.1257 0.7300 0.028 0.000 0.000 0.000 0.952 0.020
#> GSM907821 5 0.1753 0.7144 0.004 0.000 0.000 0.000 0.912 0.084
#> GSM907824 5 0.1268 0.7253 0.004 0.008 0.000 0.000 0.952 0.036
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
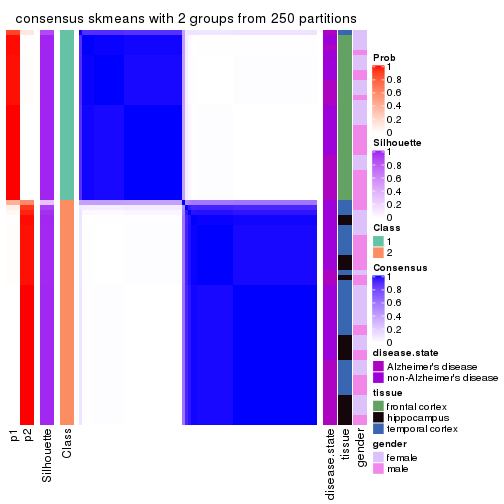
consensus_heatmap(res, k = 3)
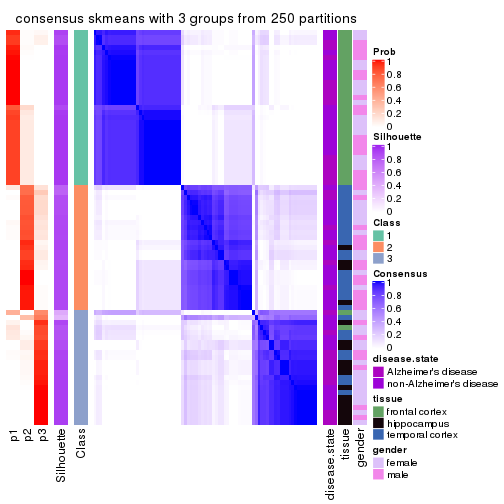
consensus_heatmap(res, k = 4)
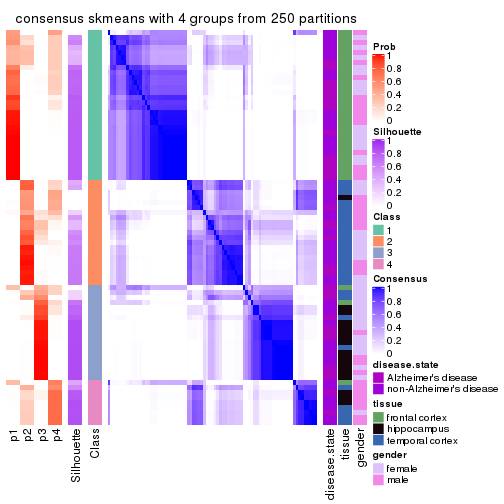
consensus_heatmap(res, k = 5)
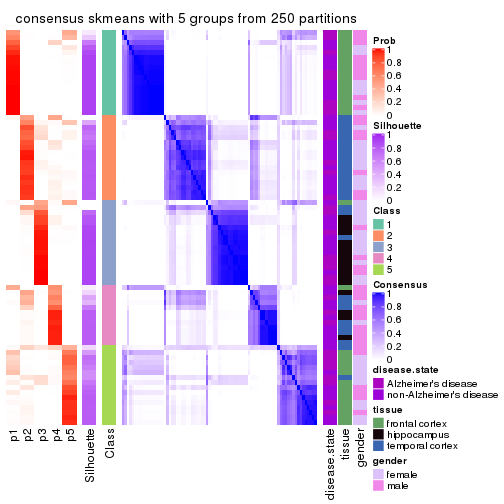
consensus_heatmap(res, k = 6)
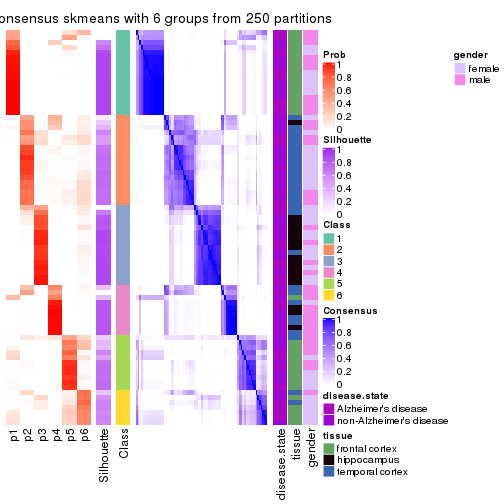
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
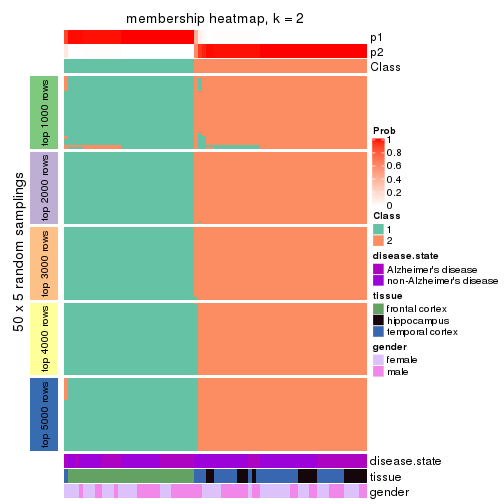
membership_heatmap(res, k = 3)
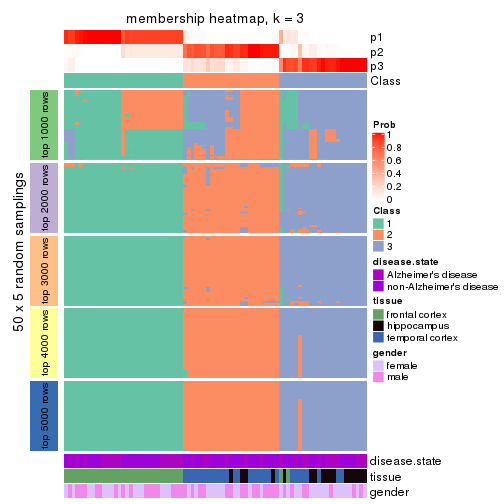
membership_heatmap(res, k = 4)
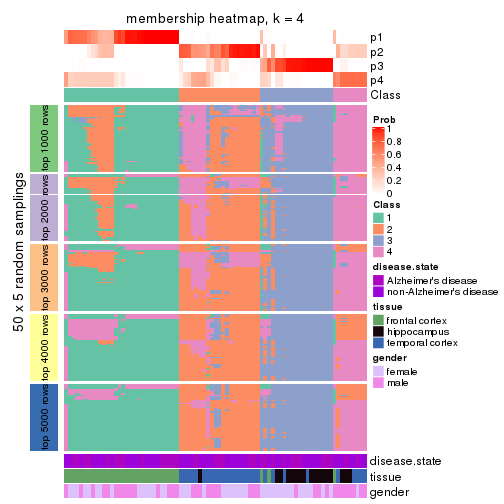
membership_heatmap(res, k = 5)
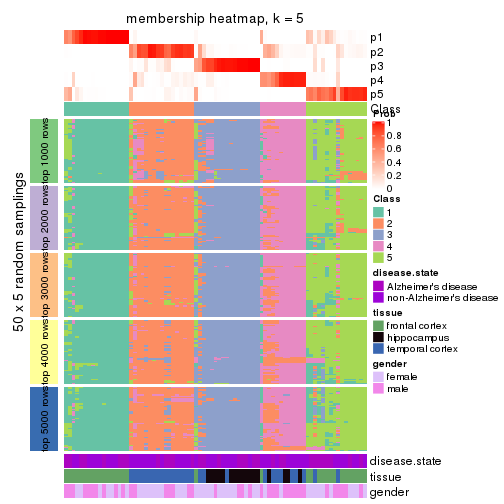
membership_heatmap(res, k = 6)
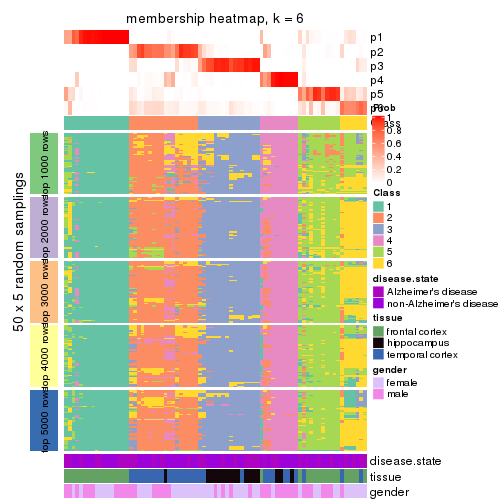
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
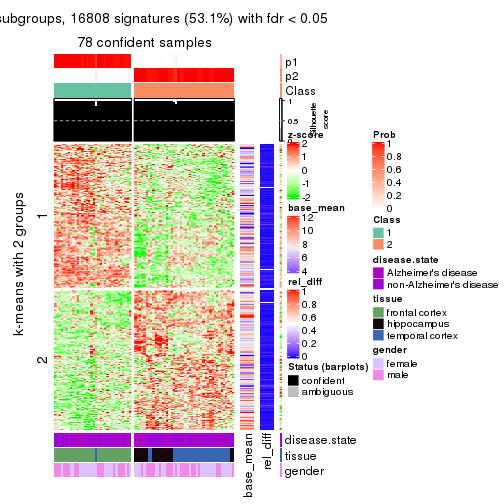
get_signatures(res, k = 3)
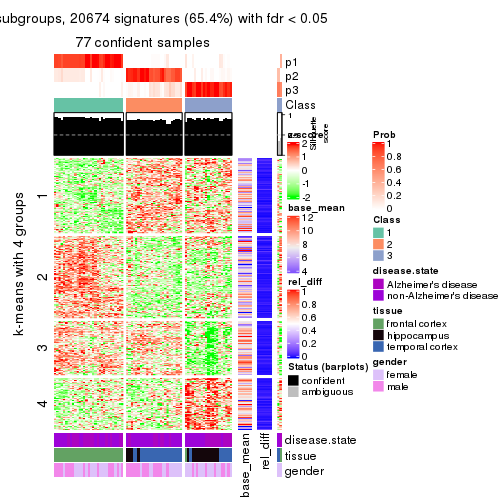
get_signatures(res, k = 4)
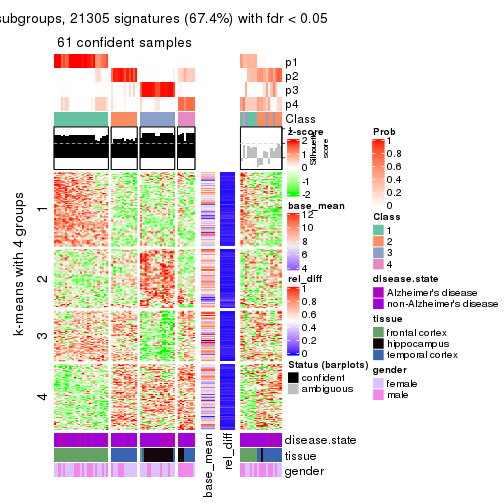
get_signatures(res, k = 5)
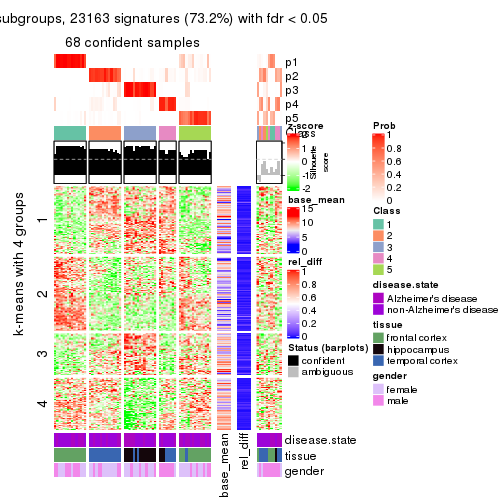
get_signatures(res, k = 6)
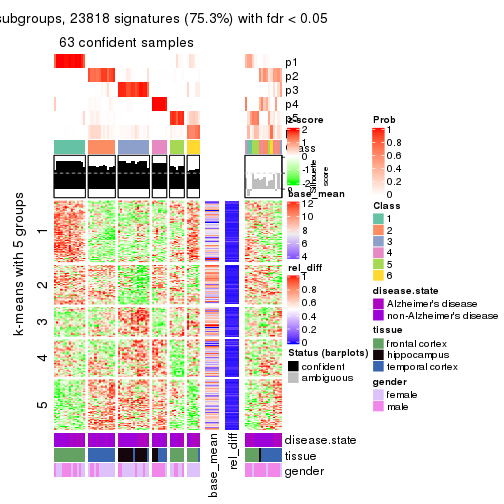
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
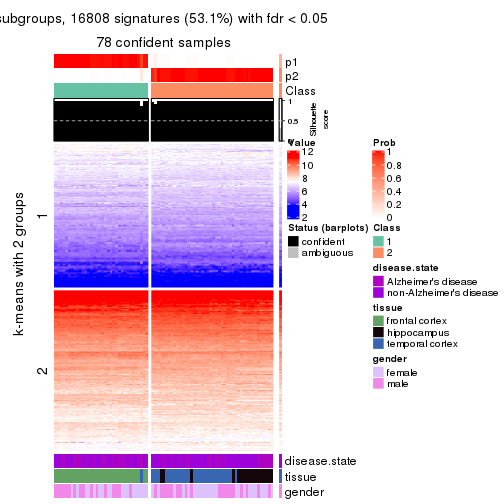
get_signatures(res, k = 3, scale_rows = FALSE)
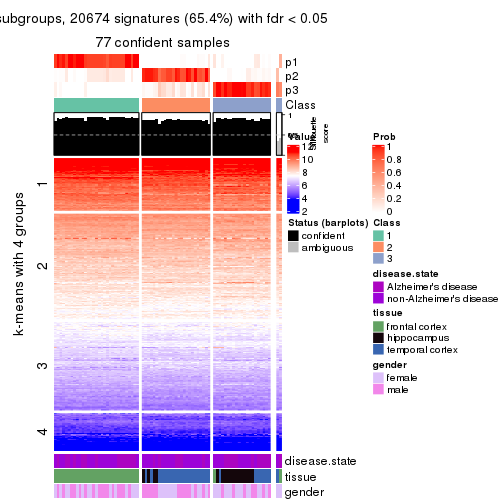
get_signatures(res, k = 4, scale_rows = FALSE)
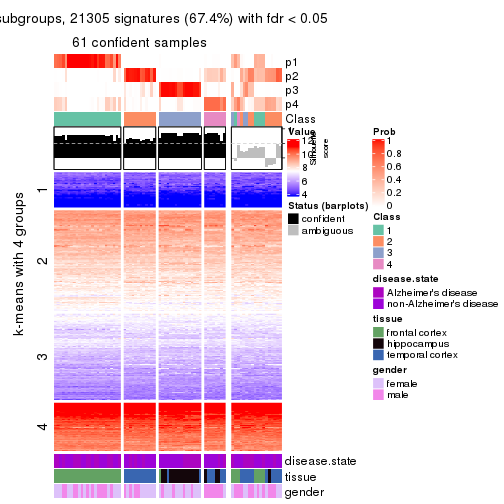
get_signatures(res, k = 5, scale_rows = FALSE)
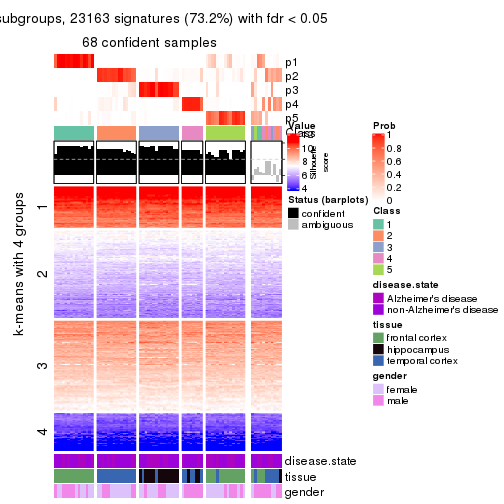
get_signatures(res, k = 6, scale_rows = FALSE)
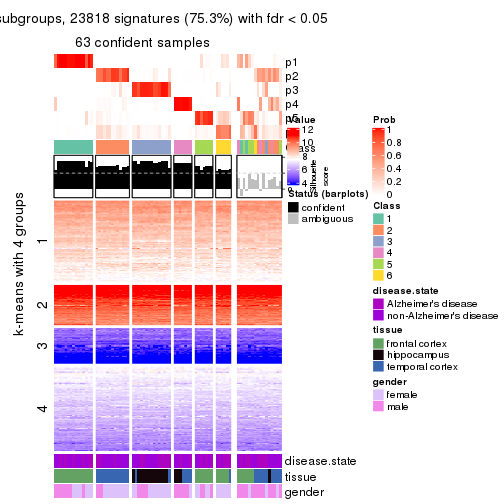
Compare the overlap of signatures from different k:
compare_signatures(res)
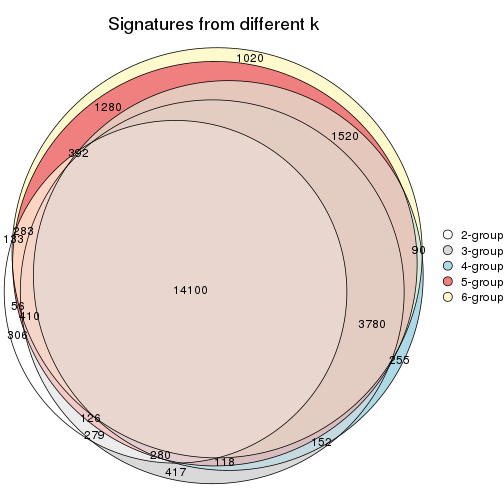
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
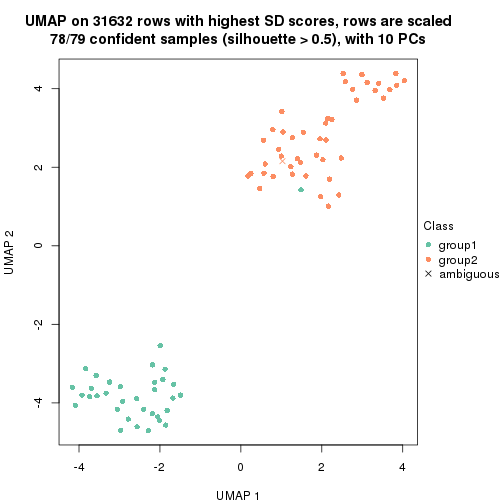
dimension_reduction(res, k = 3, method = "UMAP")
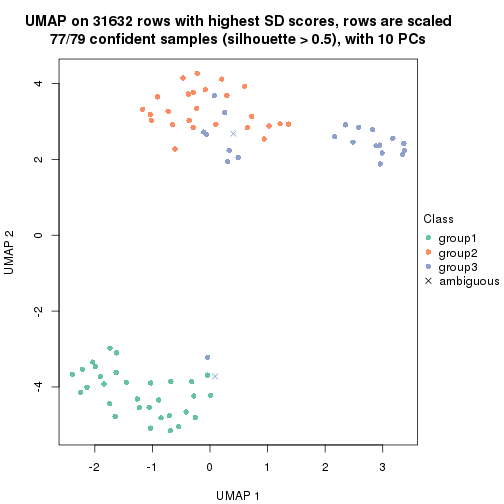
dimension_reduction(res, k = 4, method = "UMAP")
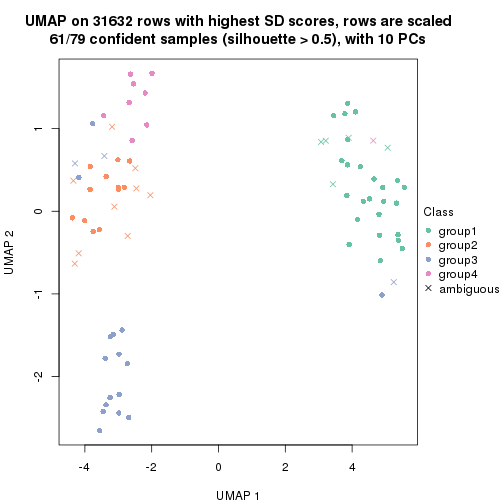
dimension_reduction(res, k = 5, method = "UMAP")
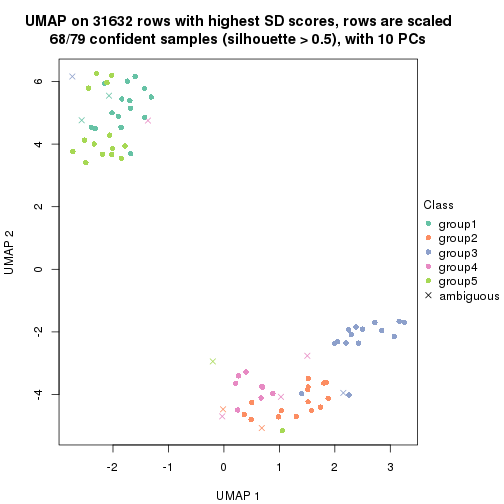
dimension_reduction(res, k = 6, method = "UMAP")
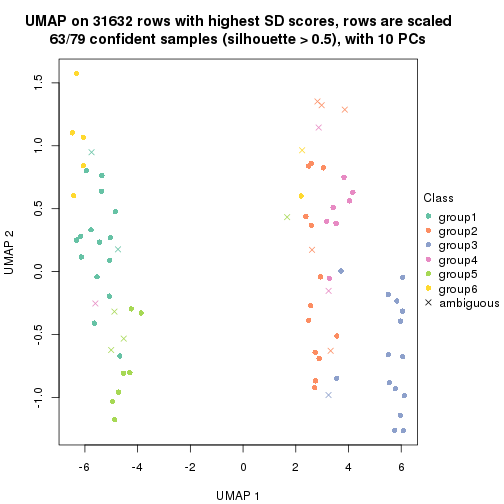
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
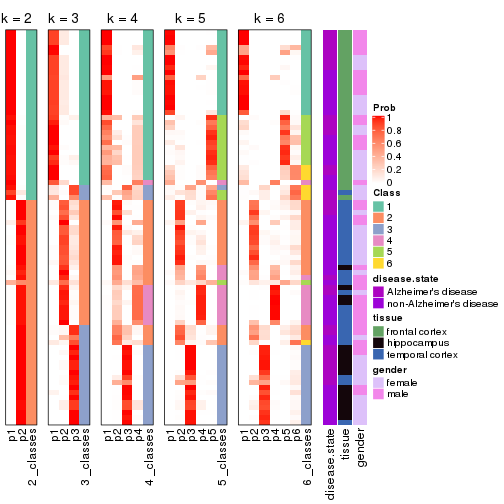
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:skmeans 78 0.471 8.21e-17 1.0000 2
#> SD:skmeans 77 0.114 4.99e-19 0.2708 3
#> SD:skmeans 61 0.332 1.33e-17 0.0269 4
#> SD:skmeans 68 0.671 3.95e-19 0.0420 5
#> SD:skmeans 63 0.547 2.17e-16 0.0153 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "pam"]
# you can also extract it by
# res = res_list["SD:pam"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'pam' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
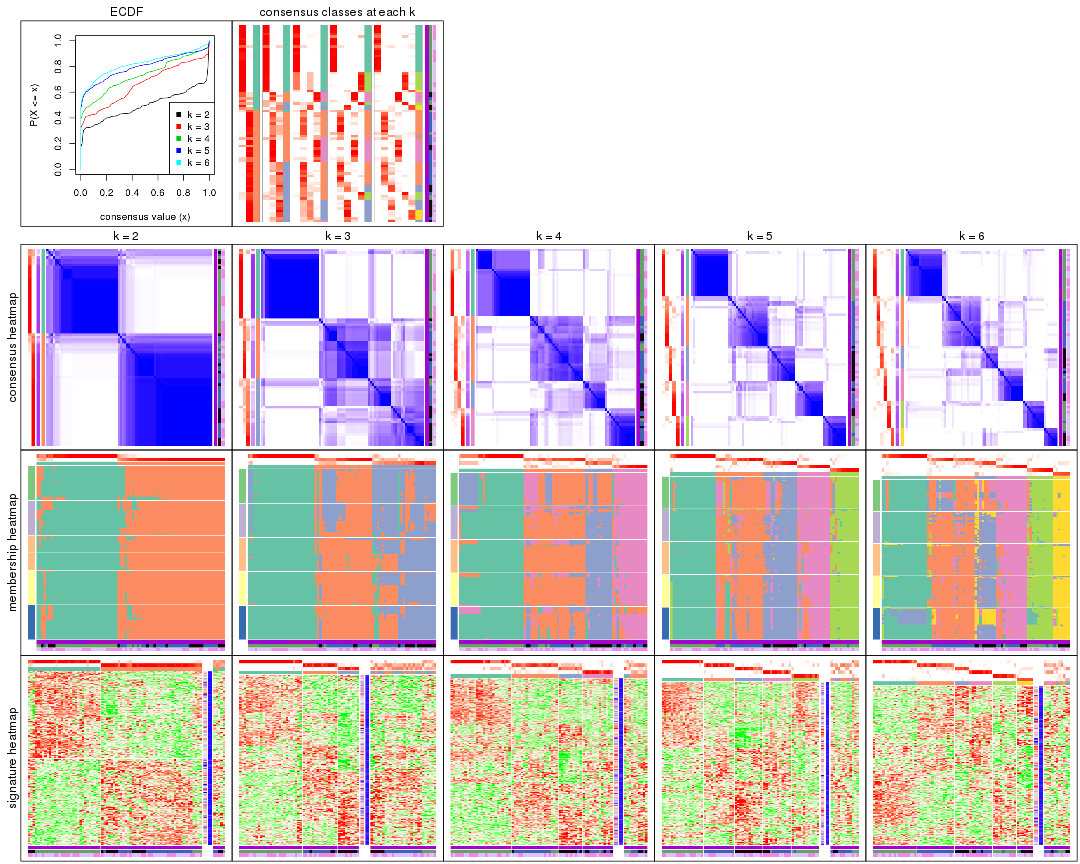
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
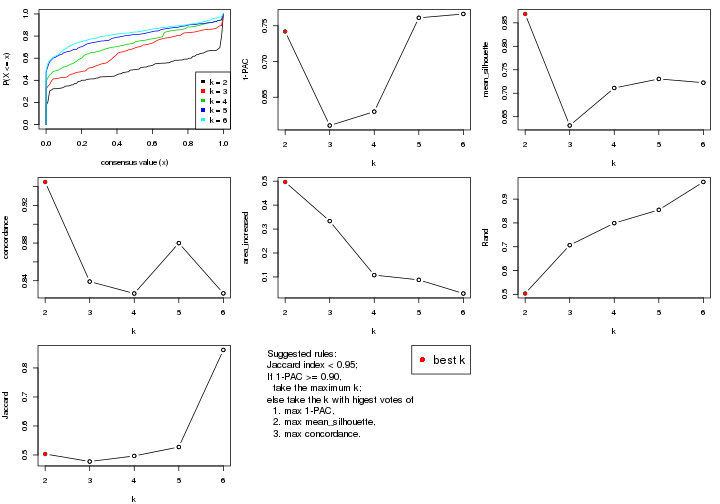
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.742 0.869 0.945 0.4967 0.503 0.503
#> 3 3 0.610 0.631 0.839 0.3333 0.707 0.477
#> 4 4 0.630 0.711 0.826 0.1076 0.799 0.497
#> 5 5 0.761 0.730 0.880 0.0878 0.855 0.527
#> 6 6 0.766 0.722 0.827 0.0307 0.972 0.862
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.9445 0.000 1.000
#> GSM907859 1 0.7139 0.7555 0.804 0.196
#> GSM907860 2 0.0000 0.9445 0.000 1.000
#> GSM907854 2 0.1414 0.9370 0.020 0.980
#> GSM907855 2 0.0376 0.9428 0.004 0.996
#> GSM907856 2 0.0000 0.9445 0.000 1.000
#> GSM907857 1 0.1414 0.9194 0.980 0.020
#> GSM907825 2 0.1414 0.9370 0.020 0.980
#> GSM907828 2 0.0000 0.9445 0.000 1.000
#> GSM907832 2 0.0000 0.9445 0.000 1.000
#> GSM907833 2 0.0000 0.9445 0.000 1.000
#> GSM907834 2 0.0000 0.9445 0.000 1.000
#> GSM907826 2 0.1414 0.9370 0.020 0.980
#> GSM907827 2 0.0000 0.9445 0.000 1.000
#> GSM907829 2 0.6247 0.8165 0.156 0.844
#> GSM907830 2 0.0000 0.9445 0.000 1.000
#> GSM907831 2 0.1414 0.9370 0.020 0.980
#> GSM907792 1 0.0000 0.9319 1.000 0.000
#> GSM907795 1 0.0000 0.9319 1.000 0.000
#> GSM907801 1 0.0000 0.9319 1.000 0.000
#> GSM907802 2 0.5629 0.8359 0.132 0.868
#> GSM907804 1 0.0000 0.9319 1.000 0.000
#> GSM907805 1 0.0000 0.9319 1.000 0.000
#> GSM907806 1 0.1414 0.9215 0.980 0.020
#> GSM907793 1 0.0376 0.9301 0.996 0.004
#> GSM907794 1 0.0000 0.9319 1.000 0.000
#> GSM907796 1 0.0000 0.9319 1.000 0.000
#> GSM907797 1 0.0000 0.9319 1.000 0.000
#> GSM907798 1 0.0000 0.9319 1.000 0.000
#> GSM907799 1 0.0000 0.9319 1.000 0.000
#> GSM907800 1 0.7815 0.6734 0.768 0.232
#> GSM907803 1 0.0000 0.9319 1.000 0.000
#> GSM907864 2 0.9977 0.0456 0.472 0.528
#> GSM907865 1 0.6623 0.7840 0.828 0.172
#> GSM907868 2 0.0000 0.9445 0.000 1.000
#> GSM907869 1 0.9866 0.2943 0.568 0.432
#> GSM907870 2 0.0000 0.9445 0.000 1.000
#> GSM907861 2 0.1414 0.9370 0.020 0.980
#> GSM907862 2 0.0000 0.9445 0.000 1.000
#> GSM907863 2 0.0000 0.9445 0.000 1.000
#> GSM907866 2 0.0000 0.9445 0.000 1.000
#> GSM907867 2 0.0000 0.9445 0.000 1.000
#> GSM907839 1 0.9970 0.1457 0.532 0.468
#> GSM907840 2 0.1414 0.9332 0.020 0.980
#> GSM907842 2 0.0000 0.9445 0.000 1.000
#> GSM907843 2 0.0000 0.9445 0.000 1.000
#> GSM907845 2 0.2043 0.9297 0.032 0.968
#> GSM907846 2 0.8555 0.5836 0.280 0.720
#> GSM907848 2 0.0000 0.9445 0.000 1.000
#> GSM907851 2 0.9635 0.3855 0.388 0.612
#> GSM907835 2 0.0376 0.9434 0.004 0.996
#> GSM907836 2 0.0376 0.9434 0.004 0.996
#> GSM907837 2 0.0000 0.9445 0.000 1.000
#> GSM907838 2 0.0000 0.9445 0.000 1.000
#> GSM907841 2 0.0000 0.9445 0.000 1.000
#> GSM907844 2 0.0000 0.9445 0.000 1.000
#> GSM907847 2 0.0000 0.9445 0.000 1.000
#> GSM907849 2 0.8813 0.5473 0.300 0.700
#> GSM907850 2 0.0000 0.9445 0.000 1.000
#> GSM907852 2 0.1414 0.9370 0.020 0.980
#> GSM907853 2 0.1414 0.9370 0.020 0.980
#> GSM907807 1 0.0000 0.9319 1.000 0.000
#> GSM907813 1 0.4690 0.8589 0.900 0.100
#> GSM907814 1 0.1414 0.9215 0.980 0.020
#> GSM907816 1 0.1414 0.9215 0.980 0.020
#> GSM907818 1 0.0000 0.9319 1.000 0.000
#> GSM907819 1 0.0000 0.9319 1.000 0.000
#> GSM907820 2 0.1843 0.9325 0.028 0.972
#> GSM907822 1 0.1414 0.9215 0.980 0.020
#> GSM907823 1 0.0000 0.9319 1.000 0.000
#> GSM907808 1 0.0000 0.9319 1.000 0.000
#> GSM907809 1 0.0000 0.9319 1.000 0.000
#> GSM907810 1 0.0000 0.9319 1.000 0.000
#> GSM907811 1 0.0000 0.9319 1.000 0.000
#> GSM907812 1 0.0000 0.9319 1.000 0.000
#> GSM907815 1 0.0000 0.9319 1.000 0.000
#> GSM907817 2 0.6712 0.7830 0.176 0.824
#> GSM907821 1 0.9732 0.3115 0.596 0.404
#> GSM907824 2 0.4939 0.8619 0.108 0.892
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.5859 0.000 0.000 1.000
#> GSM907859 2 0.1031 0.7041 0.024 0.976 0.000
#> GSM907860 3 0.5431 0.4644 0.000 0.284 0.716
#> GSM907854 3 0.0000 0.5859 0.000 0.000 1.000
#> GSM907855 3 0.3412 0.5694 0.000 0.124 0.876
#> GSM907856 3 0.3412 0.5694 0.000 0.124 0.876
#> GSM907857 3 0.5988 0.2659 0.368 0.000 0.632
#> GSM907825 3 0.5835 0.3562 0.000 0.340 0.660
#> GSM907828 2 0.0000 0.7191 0.000 1.000 0.000
#> GSM907832 2 0.3038 0.6876 0.000 0.896 0.104
#> GSM907833 2 0.3267 0.6805 0.000 0.884 0.116
#> GSM907834 3 0.6026 0.3057 0.000 0.376 0.624
#> GSM907826 3 0.6026 0.3057 0.000 0.376 0.624
#> GSM907827 3 0.6307 0.0671 0.000 0.488 0.512
#> GSM907829 3 0.8536 0.3282 0.124 0.300 0.576
#> GSM907830 2 0.0424 0.7181 0.000 0.992 0.008
#> GSM907831 3 0.0892 0.5851 0.000 0.020 0.980
#> GSM907792 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907802 3 0.9130 0.2835 0.356 0.152 0.492
#> GSM907804 1 0.1411 0.9320 0.964 0.036 0.000
#> GSM907805 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907797 1 0.0237 0.9641 0.996 0.000 0.004
#> GSM907798 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907800 1 0.4887 0.6389 0.772 0.000 0.228
#> GSM907803 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907864 2 0.0000 0.7191 0.000 1.000 0.000
#> GSM907865 2 0.6597 0.1856 0.024 0.664 0.312
#> GSM907868 3 0.4062 0.5537 0.000 0.164 0.836
#> GSM907869 3 0.6045 0.3242 0.000 0.380 0.620
#> GSM907870 2 0.0424 0.7187 0.000 0.992 0.008
#> GSM907861 3 0.0892 0.5851 0.000 0.020 0.980
#> GSM907862 3 0.4887 0.4807 0.000 0.228 0.772
#> GSM907863 3 0.5363 0.4278 0.000 0.276 0.724
#> GSM907866 3 0.3340 0.5710 0.000 0.120 0.880
#> GSM907867 3 0.2448 0.5846 0.000 0.076 0.924
#> GSM907839 2 0.1529 0.6919 0.040 0.960 0.000
#> GSM907840 2 0.0000 0.7191 0.000 1.000 0.000
#> GSM907842 2 0.0000 0.7191 0.000 1.000 0.000
#> GSM907843 2 0.0000 0.7191 0.000 1.000 0.000
#> GSM907845 3 0.6026 0.3057 0.000 0.376 0.624
#> GSM907846 2 0.1585 0.7054 0.028 0.964 0.008
#> GSM907848 2 0.5560 0.4899 0.000 0.700 0.300
#> GSM907851 2 0.8700 0.2634 0.344 0.536 0.120
#> GSM907835 3 0.6026 0.3057 0.000 0.376 0.624
#> GSM907836 3 0.6026 0.3057 0.000 0.376 0.624
#> GSM907837 2 0.6079 0.3517 0.000 0.612 0.388
#> GSM907838 2 0.3879 0.6555 0.000 0.848 0.152
#> GSM907841 3 0.6126 0.2573 0.000 0.400 0.600
#> GSM907844 3 0.5591 0.3131 0.000 0.304 0.696
#> GSM907847 2 0.3551 0.6687 0.000 0.868 0.132
#> GSM907849 2 0.0424 0.7185 0.008 0.992 0.000
#> GSM907850 2 0.6079 0.3517 0.000 0.612 0.388
#> GSM907852 2 0.6079 0.3517 0.000 0.612 0.388
#> GSM907853 2 0.6079 0.3517 0.000 0.612 0.388
#> GSM907807 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907813 2 0.6140 0.1848 0.404 0.596 0.000
#> GSM907814 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907820 2 0.6608 0.3907 0.016 0.628 0.356
#> GSM907822 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.9675 1.000 0.000 0.000
#> GSM907815 1 0.1031 0.9468 0.976 0.000 0.024
#> GSM907817 1 0.7820 0.0999 0.544 0.056 0.400
#> GSM907821 3 0.9177 0.2371 0.400 0.148 0.452
#> GSM907824 3 0.9810 0.0387 0.240 0.372 0.388
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.4605 0.8009 0.000 0.336 0.664 0.000
#> GSM907859 4 0.0000 0.8546 0.000 0.000 0.000 1.000
#> GSM907860 4 0.7474 0.1154 0.000 0.292 0.212 0.496
#> GSM907854 3 0.4761 0.7677 0.000 0.372 0.628 0.000
#> GSM907855 3 0.4761 0.8023 0.000 0.332 0.664 0.004
#> GSM907856 3 0.4761 0.8023 0.000 0.332 0.664 0.004
#> GSM907857 3 0.2647 0.6895 0.000 0.120 0.880 0.000
#> GSM907825 2 0.2214 0.7015 0.000 0.928 0.044 0.028
#> GSM907828 4 0.0336 0.8537 0.000 0.008 0.000 0.992
#> GSM907832 2 0.4925 0.3878 0.000 0.572 0.000 0.428
#> GSM907833 2 0.4998 0.2158 0.000 0.512 0.000 0.488
#> GSM907834 2 0.0707 0.7203 0.000 0.980 0.000 0.020
#> GSM907826 2 0.1297 0.7145 0.000 0.964 0.016 0.020
#> GSM907827 2 0.3443 0.7177 0.000 0.848 0.016 0.136
#> GSM907829 2 0.5323 0.5232 0.020 0.628 0.352 0.000
#> GSM907830 4 0.0336 0.8529 0.000 0.008 0.000 0.992
#> GSM907831 2 0.2469 0.6052 0.000 0.892 0.108 0.000
#> GSM907792 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907802 2 0.6407 0.4633 0.084 0.584 0.332 0.000
#> GSM907804 1 0.1118 0.8537 0.964 0.000 0.000 0.036
#> GSM907805 1 0.1792 0.8458 0.932 0.000 0.068 0.000
#> GSM907806 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907794 1 0.4564 0.7113 0.672 0.000 0.328 0.000
#> GSM907796 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907797 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907798 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907799 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907800 1 0.3831 0.6715 0.792 0.204 0.004 0.000
#> GSM907803 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.8546 0.000 0.000 0.000 1.000
#> GSM907865 4 0.0707 0.8393 0.000 0.020 0.000 0.980
#> GSM907868 3 0.5578 0.7890 0.000 0.312 0.648 0.040
#> GSM907869 3 0.2647 0.6895 0.000 0.120 0.880 0.000
#> GSM907870 4 0.3172 0.7350 0.000 0.160 0.000 0.840
#> GSM907861 2 0.3311 0.5090 0.000 0.828 0.172 0.000
#> GSM907862 2 0.6439 0.4997 0.000 0.648 0.172 0.180
#> GSM907863 2 0.6678 0.4801 0.000 0.620 0.172 0.208
#> GSM907866 3 0.4605 0.8009 0.000 0.336 0.664 0.000
#> GSM907867 3 0.6350 0.7360 0.000 0.364 0.564 0.072
#> GSM907839 4 0.0000 0.8546 0.000 0.000 0.000 1.000
#> GSM907840 4 0.0000 0.8546 0.000 0.000 0.000 1.000
#> GSM907842 4 0.0000 0.8546 0.000 0.000 0.000 1.000
#> GSM907843 4 0.1211 0.8388 0.000 0.040 0.000 0.960
#> GSM907845 2 0.5130 0.5666 0.000 0.668 0.312 0.020
#> GSM907846 4 0.6346 0.5174 0.152 0.192 0.000 0.656
#> GSM907848 2 0.3219 0.7318 0.000 0.836 0.000 0.164
#> GSM907851 4 0.7799 0.0754 0.252 0.348 0.000 0.400
#> GSM907835 2 0.0921 0.7244 0.000 0.972 0.000 0.028
#> GSM907836 2 0.1724 0.7187 0.000 0.948 0.020 0.032
#> GSM907837 2 0.2921 0.7375 0.000 0.860 0.000 0.140
#> GSM907838 2 0.4907 0.4682 0.000 0.580 0.000 0.420
#> GSM907841 3 0.6975 0.6109 0.000 0.200 0.584 0.216
#> GSM907844 2 0.4888 0.6863 0.000 0.780 0.096 0.124
#> GSM907847 2 0.4564 0.5523 0.000 0.672 0.000 0.328
#> GSM907849 4 0.2412 0.8075 0.008 0.084 0.000 0.908
#> GSM907850 2 0.2647 0.7403 0.000 0.880 0.000 0.120
#> GSM907852 2 0.2647 0.7403 0.000 0.880 0.000 0.120
#> GSM907853 2 0.2647 0.7403 0.000 0.880 0.000 0.120
#> GSM907807 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907813 4 0.2216 0.7786 0.092 0.000 0.000 0.908
#> GSM907814 1 0.0592 0.8628 0.984 0.000 0.000 0.016
#> GSM907816 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907818 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907819 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907820 2 0.4003 0.7152 0.080 0.856 0.028 0.036
#> GSM907822 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0000 0.8730 1.000 0.000 0.000 0.000
#> GSM907812 1 0.4605 0.7064 0.664 0.000 0.336 0.000
#> GSM907815 3 0.3311 0.3496 0.172 0.000 0.828 0.000
#> GSM907817 2 0.4507 0.6200 0.168 0.788 0.044 0.000
#> GSM907821 1 0.7527 0.3959 0.452 0.192 0.356 0.000
#> GSM907824 2 0.2976 0.7026 0.008 0.872 0.120 0.000
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 0.814 0.000 0.000 1.000 0.000 0.000
#> GSM907859 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907860 3 0.4444 0.716 0.000 0.072 0.748 0.180 0.000
#> GSM907854 3 0.0963 0.809 0.000 0.036 0.964 0.000 0.000
#> GSM907855 3 0.2230 0.775 0.000 0.116 0.884 0.000 0.000
#> GSM907856 3 0.0000 0.814 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0794 0.808 0.000 0.000 0.972 0.000 0.028
#> GSM907825 2 0.2561 0.655 0.000 0.856 0.144 0.000 0.000
#> GSM907828 4 0.0880 0.826 0.000 0.032 0.000 0.968 0.000
#> GSM907832 2 0.4288 0.260 0.000 0.612 0.000 0.384 0.004
#> GSM907833 2 0.3969 0.414 0.000 0.692 0.000 0.304 0.004
#> GSM907834 2 0.0162 0.747 0.000 0.996 0.000 0.000 0.004
#> GSM907826 2 0.0880 0.745 0.000 0.968 0.032 0.000 0.000
#> GSM907827 2 0.3119 0.703 0.000 0.860 0.068 0.072 0.000
#> GSM907829 5 0.0162 0.902 0.000 0.004 0.000 0.000 0.996
#> GSM907830 4 0.0609 0.829 0.000 0.020 0.000 0.980 0.000
#> GSM907831 2 0.4219 0.117 0.000 0.584 0.416 0.000 0.000
#> GSM907792 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.3366 0.666 0.000 0.232 0.000 0.000 0.768
#> GSM907804 1 0.1168 0.928 0.960 0.000 0.000 0.032 0.008
#> GSM907805 1 0.4060 0.372 0.640 0.000 0.000 0.000 0.360
#> GSM907806 1 0.0162 0.959 0.996 0.004 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.1908 0.846 0.092 0.000 0.000 0.000 0.908
#> GSM907796 5 0.0162 0.903 0.004 0.000 0.000 0.000 0.996
#> GSM907797 5 0.0404 0.902 0.012 0.000 0.000 0.000 0.988
#> GSM907798 5 0.0162 0.903 0.004 0.000 0.000 0.000 0.996
#> GSM907799 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907800 1 0.3513 0.718 0.800 0.180 0.000 0.000 0.020
#> GSM907803 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907865 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907868 3 0.0807 0.816 0.000 0.012 0.976 0.012 0.000
#> GSM907869 3 0.1792 0.770 0.000 0.000 0.916 0.000 0.084
#> GSM907870 4 0.4060 0.465 0.000 0.360 0.000 0.640 0.000
#> GSM907861 3 0.4268 0.258 0.000 0.444 0.556 0.000 0.000
#> GSM907862 3 0.4665 0.700 0.000 0.112 0.740 0.148 0.000
#> GSM907863 3 0.5329 0.627 0.000 0.144 0.672 0.184 0.000
#> GSM907866 3 0.0000 0.814 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.3710 0.709 0.000 0.192 0.784 0.024 0.000
#> GSM907839 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907840 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907842 4 0.0000 0.833 0.000 0.000 0.000 1.000 0.000
#> GSM907843 4 0.1544 0.805 0.000 0.068 0.000 0.932 0.000
#> GSM907845 2 0.3210 0.613 0.000 0.788 0.000 0.000 0.212
#> GSM907846 4 0.5335 0.537 0.096 0.260 0.000 0.644 0.000
#> GSM907848 2 0.1205 0.734 0.000 0.956 0.000 0.040 0.004
#> GSM907851 2 0.6177 0.310 0.232 0.556 0.000 0.212 0.000
#> GSM907835 2 0.0162 0.747 0.000 0.996 0.000 0.000 0.004
#> GSM907836 2 0.2450 0.721 0.000 0.896 0.076 0.028 0.000
#> GSM907837 2 0.1484 0.734 0.000 0.944 0.008 0.048 0.000
#> GSM907838 4 0.4227 0.165 0.000 0.420 0.000 0.580 0.000
#> GSM907841 3 0.4392 0.335 0.000 0.008 0.612 0.380 0.000
#> GSM907844 2 0.5176 -0.174 0.000 0.492 0.468 0.040 0.000
#> GSM907847 2 0.3048 0.601 0.000 0.820 0.000 0.176 0.004
#> GSM907849 4 0.4418 0.503 0.016 0.332 0.000 0.652 0.000
#> GSM907850 2 0.0000 0.747 0.000 1.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.747 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.0162 0.747 0.000 0.996 0.000 0.000 0.004
#> GSM907807 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.3274 0.632 0.220 0.000 0.000 0.780 0.000
#> GSM907814 1 0.0162 0.959 0.996 0.000 0.000 0.004 0.000
#> GSM907816 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.0162 0.903 0.004 0.000 0.000 0.000 0.996
#> GSM907819 5 0.1341 0.877 0.056 0.000 0.000 0.000 0.944
#> GSM907820 2 0.5235 0.385 0.360 0.596 0.000 0.016 0.028
#> GSM907822 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.0000 0.962 1.000 0.000 0.000 0.000 0.000
#> GSM907812 5 0.0404 0.902 0.012 0.000 0.000 0.000 0.988
#> GSM907815 5 0.3508 0.680 0.000 0.000 0.252 0.000 0.748
#> GSM907817 2 0.6508 0.250 0.364 0.484 0.012 0.000 0.140
#> GSM907821 5 0.0162 0.902 0.000 0.004 0.000 0.000 0.996
#> GSM907824 5 0.3774 0.576 0.000 0.296 0.000 0.000 0.704
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 6 0.2219 0.8820 0.000 0.000 0.136 0.000 0.000 0.864
#> GSM907859 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907860 3 0.2563 0.6985 0.000 0.000 0.876 0.072 0.000 0.052
#> GSM907854 3 0.4184 0.2053 0.000 0.016 0.576 0.000 0.000 0.408
#> GSM907855 3 0.3843 -0.0144 0.000 0.000 0.548 0.000 0.000 0.452
#> GSM907856 6 0.2562 0.8515 0.000 0.000 0.172 0.000 0.000 0.828
#> GSM907857 6 0.2135 0.8857 0.000 0.000 0.128 0.000 0.000 0.872
#> GSM907825 2 0.3349 0.7031 0.000 0.748 0.244 0.000 0.000 0.008
#> GSM907828 4 0.1007 0.8139 0.000 0.044 0.000 0.956 0.000 0.000
#> GSM907832 2 0.3217 0.5375 0.000 0.768 0.000 0.224 0.000 0.008
#> GSM907833 2 0.2302 0.6621 0.000 0.872 0.000 0.120 0.000 0.008
#> GSM907834 2 0.0717 0.7314 0.000 0.976 0.016 0.000 0.000 0.008
#> GSM907826 2 0.2854 0.7296 0.000 0.792 0.208 0.000 0.000 0.000
#> GSM907827 2 0.4468 0.6899 0.000 0.696 0.212 0.092 0.000 0.000
#> GSM907829 5 0.0260 0.8639 0.000 0.008 0.000 0.000 0.992 0.000
#> GSM907830 4 0.1686 0.7801 0.000 0.012 0.064 0.924 0.000 0.000
#> GSM907831 2 0.3852 0.5508 0.000 0.612 0.384 0.000 0.000 0.004
#> GSM907792 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.5375 0.5324 0.000 0.276 0.008 0.000 0.592 0.124
#> GSM907804 1 0.3072 0.8578 0.852 0.000 0.004 0.020 0.020 0.104
#> GSM907805 1 0.3859 0.5295 0.692 0.020 0.000 0.000 0.288 0.000
#> GSM907806 1 0.0858 0.9240 0.968 0.004 0.000 0.000 0.000 0.028
#> GSM907793 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.2956 0.7851 0.120 0.000 0.000 0.000 0.840 0.040
#> GSM907796 5 0.0260 0.8667 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907797 5 0.0713 0.8633 0.028 0.000 0.000 0.000 0.972 0.000
#> GSM907798 5 0.0260 0.8667 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907799 1 0.1327 0.9129 0.936 0.000 0.000 0.000 0.000 0.064
#> GSM907800 1 0.6041 0.5667 0.640 0.048 0.164 0.000 0.028 0.120
#> GSM907803 1 0.1327 0.9129 0.936 0.000 0.000 0.000 0.000 0.064
#> GSM907864 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.2700 0.6159 0.000 0.004 0.836 0.004 0.000 0.156
#> GSM907869 6 0.2442 0.8768 0.000 0.000 0.144 0.000 0.004 0.852
#> GSM907870 4 0.4066 0.3519 0.000 0.392 0.012 0.596 0.000 0.000
#> GSM907861 3 0.2053 0.6238 0.000 0.108 0.888 0.000 0.000 0.004
#> GSM907862 3 0.2436 0.6977 0.000 0.000 0.880 0.088 0.000 0.032
#> GSM907863 3 0.2615 0.6738 0.000 0.004 0.852 0.136 0.000 0.008
#> GSM907866 6 0.2135 0.8857 0.000 0.000 0.128 0.000 0.000 0.872
#> GSM907867 3 0.1605 0.6581 0.000 0.044 0.936 0.004 0.000 0.016
#> GSM907839 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907840 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.0000 0.8242 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907843 4 0.1588 0.7954 0.000 0.072 0.004 0.924 0.000 0.000
#> GSM907845 2 0.2191 0.6932 0.000 0.876 0.000 0.000 0.120 0.004
#> GSM907846 4 0.6505 0.2105 0.096 0.352 0.048 0.488 0.008 0.008
#> GSM907848 2 0.0862 0.7238 0.000 0.972 0.004 0.008 0.000 0.016
#> GSM907851 2 0.5946 0.3118 0.176 0.544 0.020 0.260 0.000 0.000
#> GSM907835 2 0.2092 0.7435 0.000 0.876 0.124 0.000 0.000 0.000
#> GSM907836 2 0.3653 0.7159 0.000 0.748 0.228 0.020 0.000 0.004
#> GSM907837 2 0.3672 0.6685 0.000 0.688 0.304 0.008 0.000 0.000
#> GSM907838 3 0.6560 0.3475 0.000 0.156 0.488 0.292 0.000 0.064
#> GSM907841 6 0.3190 0.7383 0.000 0.000 0.044 0.136 0.000 0.820
#> GSM907844 2 0.5077 0.4820 0.000 0.524 0.404 0.068 0.000 0.004
#> GSM907847 2 0.1265 0.7108 0.000 0.948 0.000 0.044 0.000 0.008
#> GSM907849 4 0.4607 0.3612 0.036 0.380 0.004 0.580 0.000 0.000
#> GSM907850 2 0.2697 0.7344 0.000 0.812 0.188 0.000 0.000 0.000
#> GSM907852 2 0.2762 0.7326 0.000 0.804 0.196 0.000 0.000 0.000
#> GSM907853 2 0.0000 0.7279 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.2048 0.7192 0.120 0.000 0.000 0.880 0.000 0.000
#> GSM907814 1 0.0146 0.9348 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907816 1 0.1327 0.9129 0.936 0.000 0.000 0.000 0.000 0.064
#> GSM907818 5 0.1610 0.8338 0.000 0.000 0.000 0.000 0.916 0.084
#> GSM907819 5 0.1610 0.8327 0.084 0.000 0.000 0.000 0.916 0.000
#> GSM907820 2 0.6173 0.3466 0.232 0.584 0.004 0.004 0.048 0.128
#> GSM907822 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9363 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0146 0.9356 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907811 1 0.1866 0.8966 0.908 0.000 0.000 0.000 0.008 0.084
#> GSM907812 5 0.0713 0.8633 0.028 0.000 0.000 0.000 0.972 0.000
#> GSM907815 6 0.2730 0.6969 0.000 0.000 0.000 0.000 0.192 0.808
#> GSM907817 2 0.8799 0.1558 0.236 0.276 0.180 0.000 0.180 0.128
#> GSM907821 5 0.0260 0.8638 0.000 0.008 0.000 0.000 0.992 0.000
#> GSM907824 5 0.6496 0.4405 0.000 0.144 0.176 0.000 0.560 0.120
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
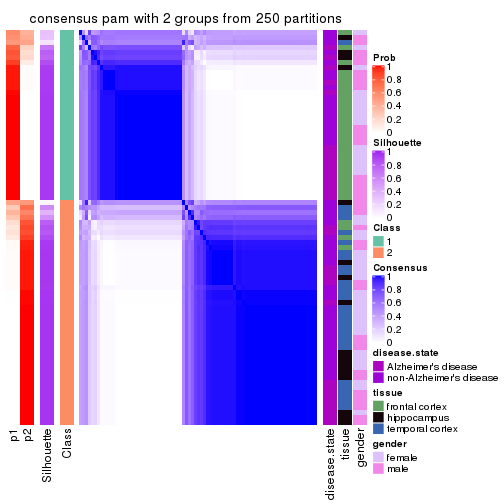
consensus_heatmap(res, k = 3)
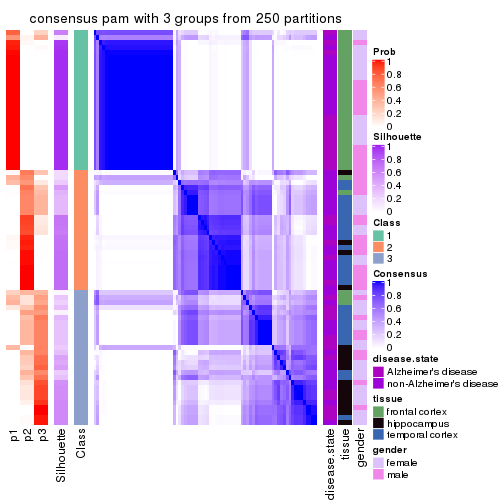
consensus_heatmap(res, k = 4)
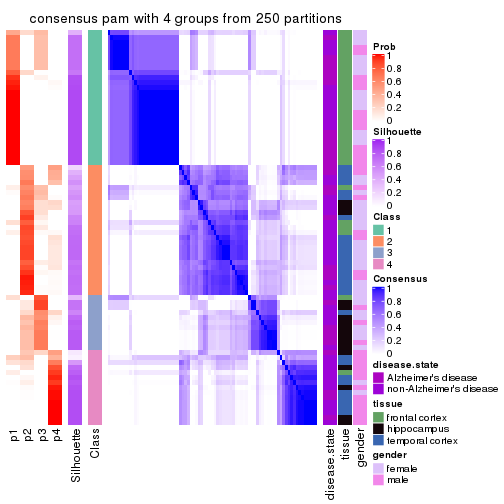
consensus_heatmap(res, k = 5)
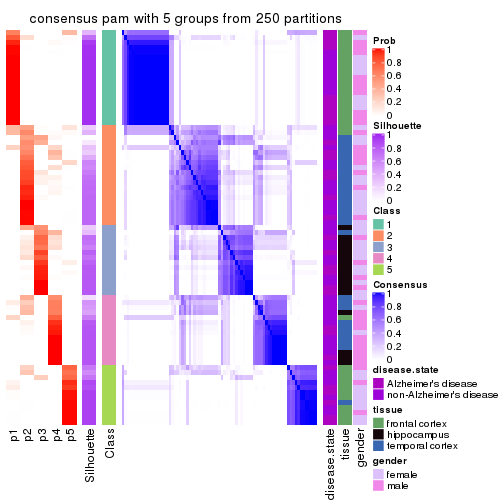
consensus_heatmap(res, k = 6)
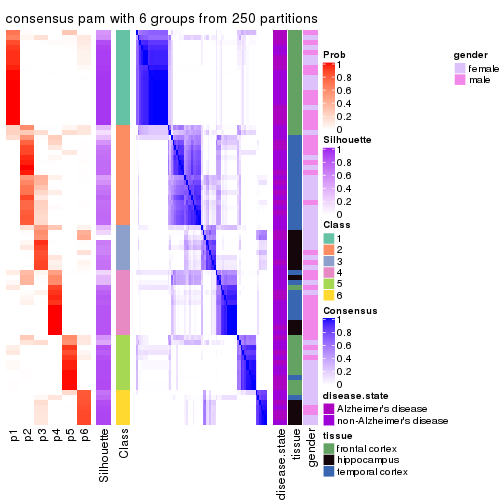
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
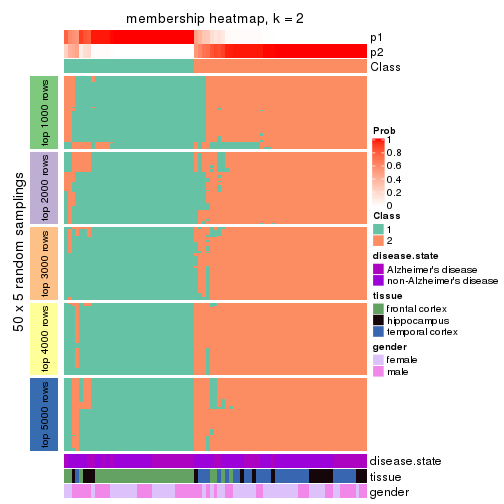
membership_heatmap(res, k = 3)
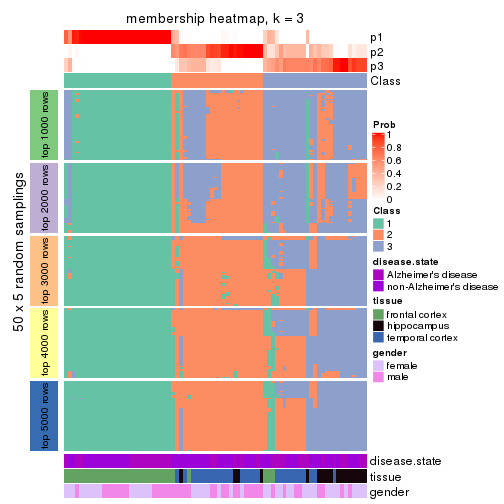
membership_heatmap(res, k = 4)
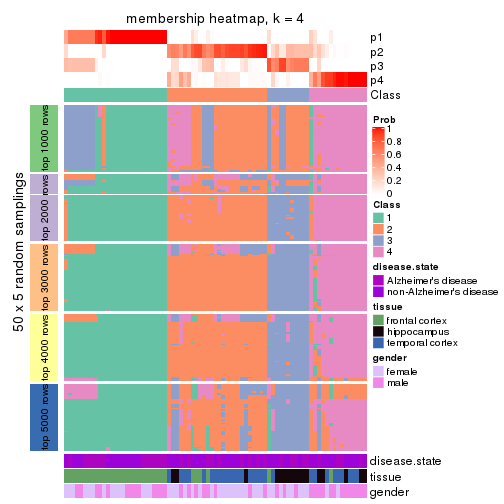
membership_heatmap(res, k = 5)
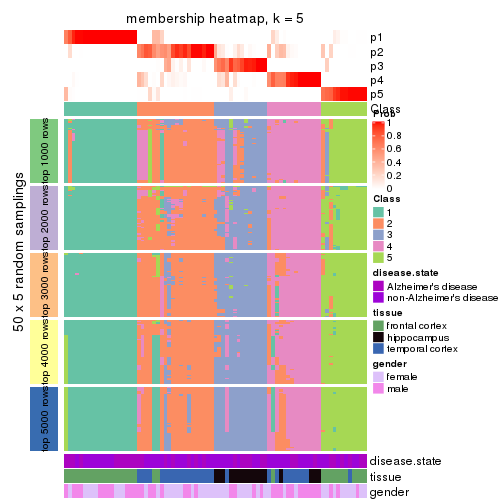
membership_heatmap(res, k = 6)
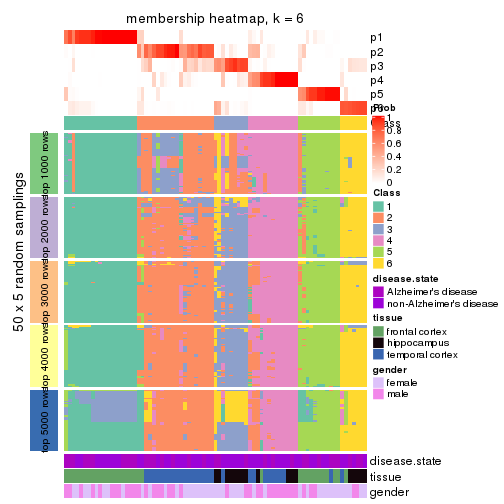
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
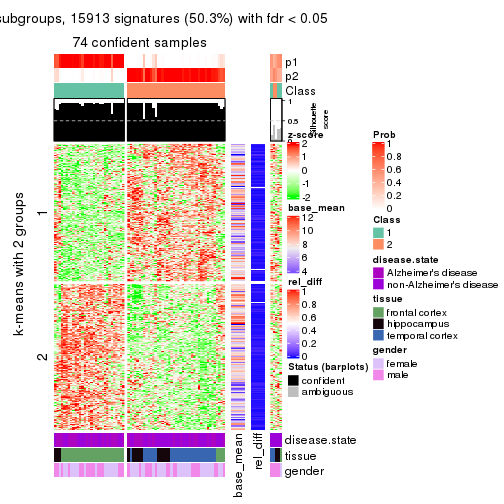
get_signatures(res, k = 3)
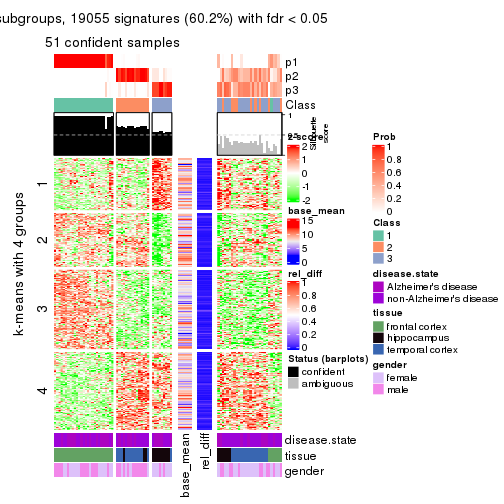
get_signatures(res, k = 4)
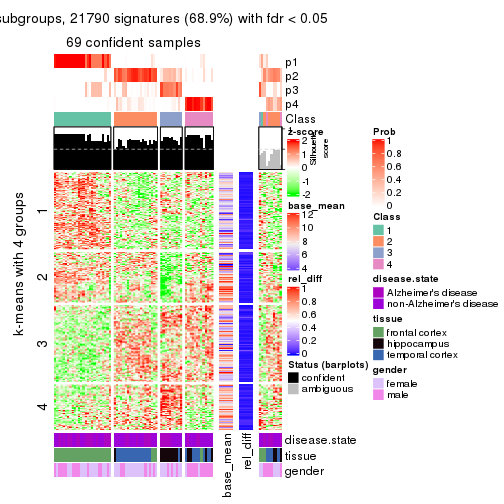
get_signatures(res, k = 5)
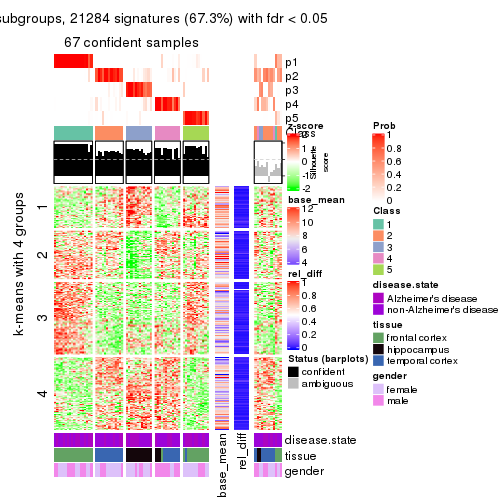
get_signatures(res, k = 6)
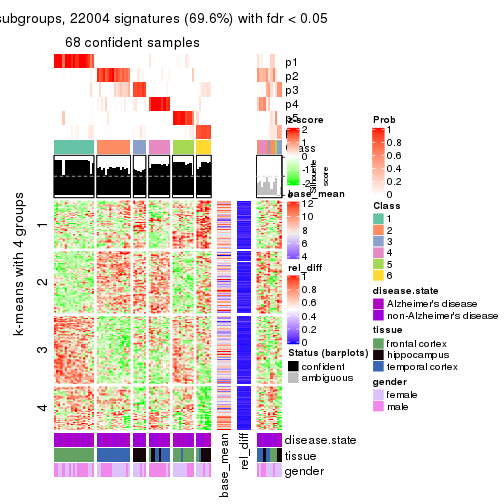
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
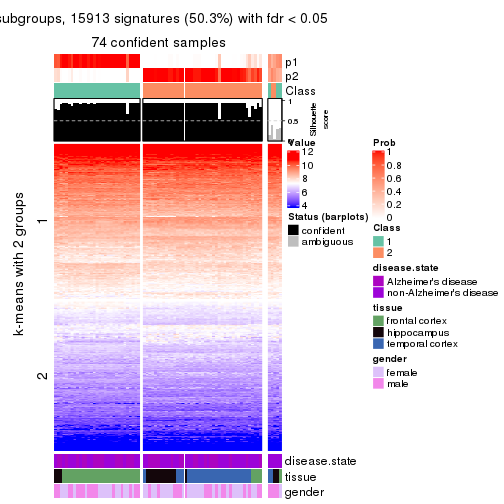
get_signatures(res, k = 3, scale_rows = FALSE)
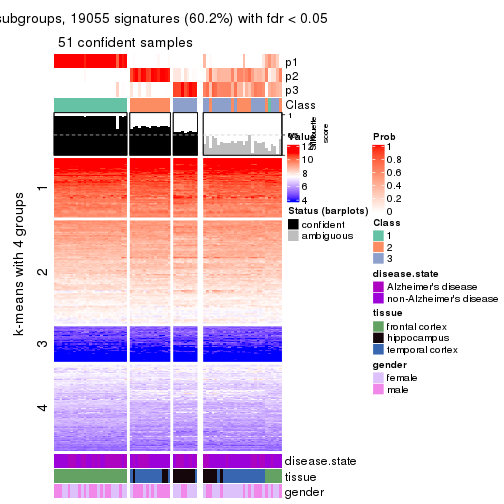
get_signatures(res, k = 4, scale_rows = FALSE)
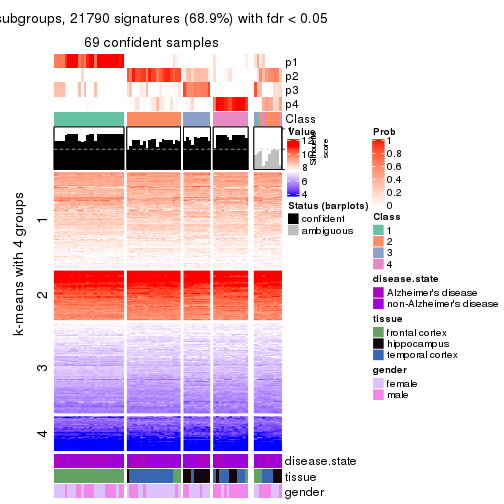
get_signatures(res, k = 5, scale_rows = FALSE)
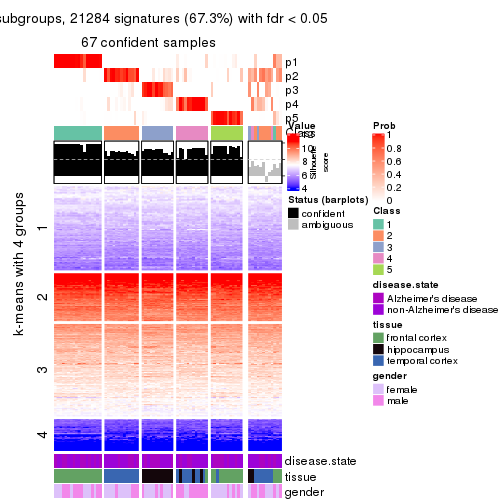
get_signatures(res, k = 6, scale_rows = FALSE)
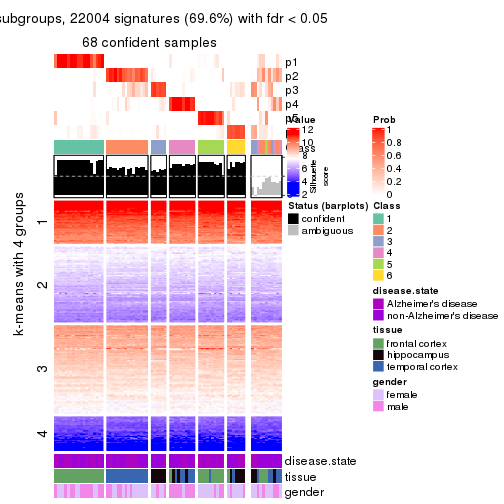
Compare the overlap of signatures from different k:
compare_signatures(res)
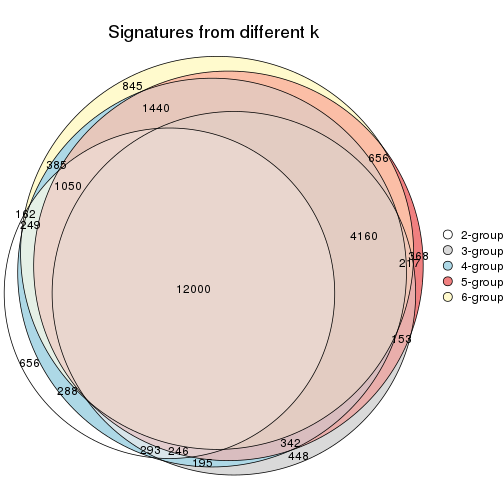
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
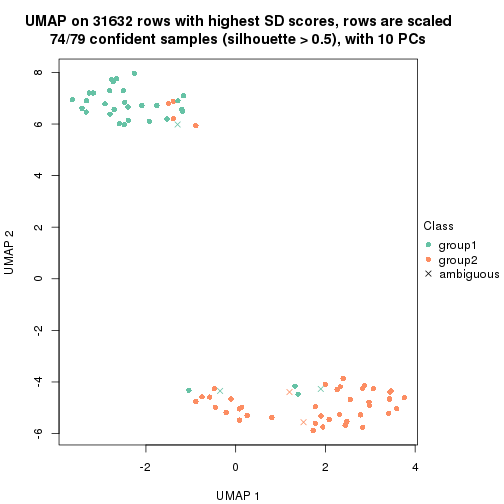
dimension_reduction(res, k = 3, method = "UMAP")
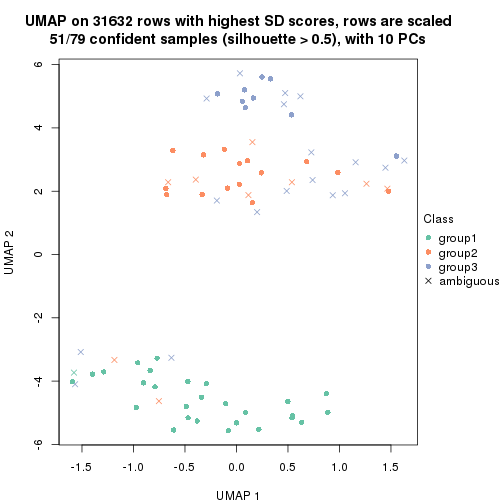
dimension_reduction(res, k = 4, method = "UMAP")
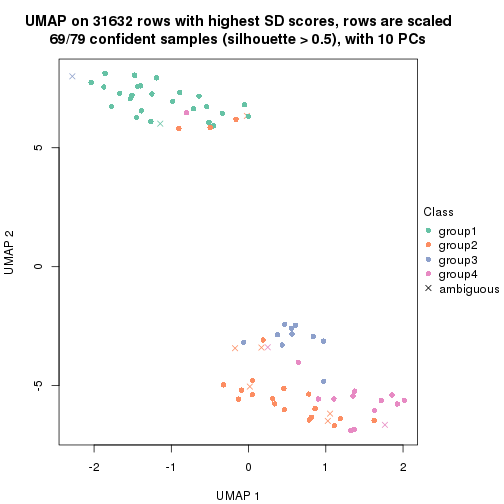
dimension_reduction(res, k = 5, method = "UMAP")
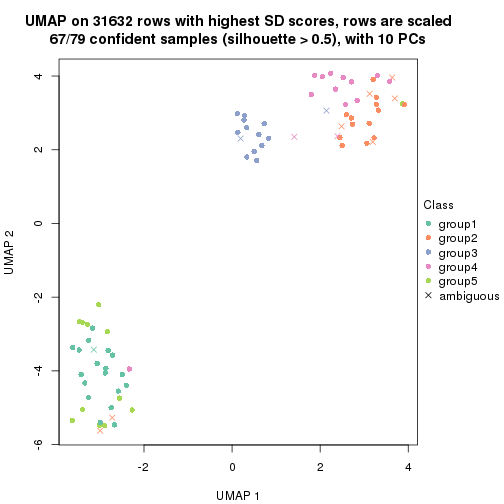
dimension_reduction(res, k = 6, method = "UMAP")
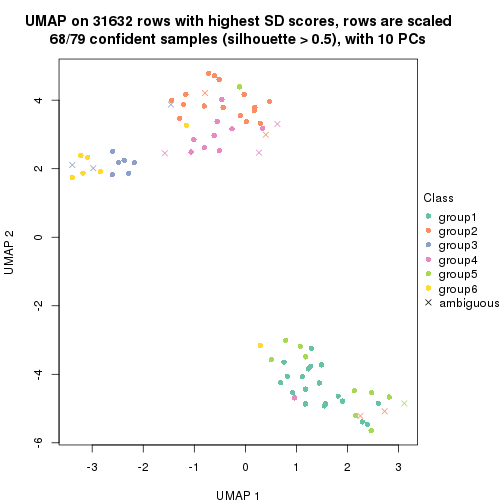
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
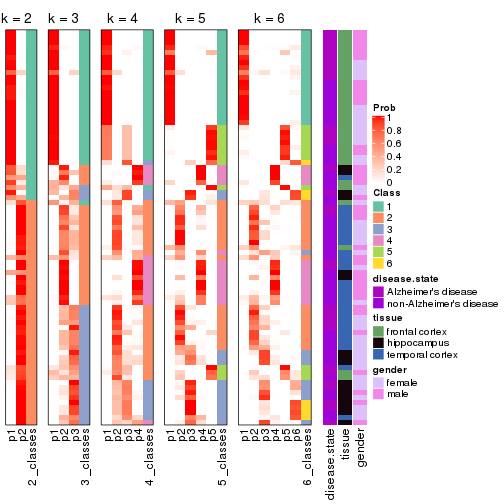
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:pam 74 0.319 1.56e-11 0.42703 2
#> SD:pam 51 0.440 3.49e-15 0.04821 3
#> SD:pam 69 0.183 1.03e-16 0.00576 4
#> SD:pam 67 0.524 6.28e-20 0.02146 5
#> SD:pam 68 0.517 3.34e-17 0.04440 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "mclust"]
# you can also extract it by
# res = res_list["SD:mclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'mclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
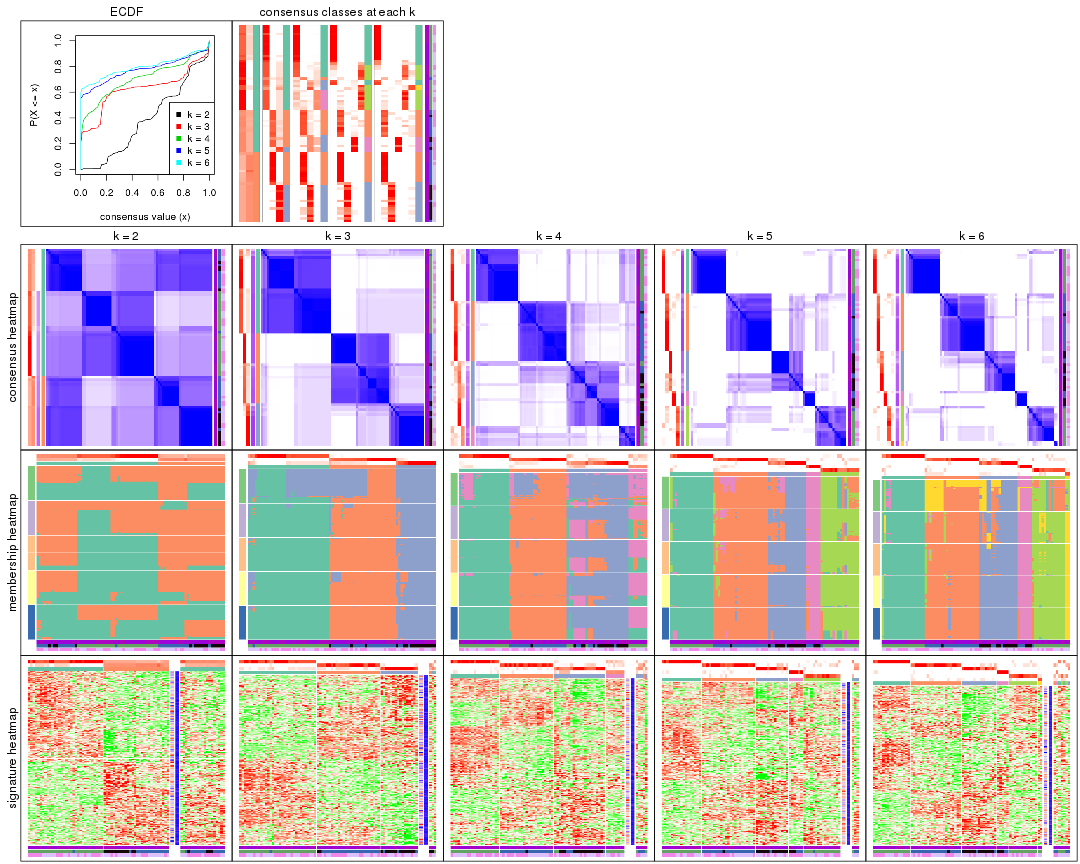
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
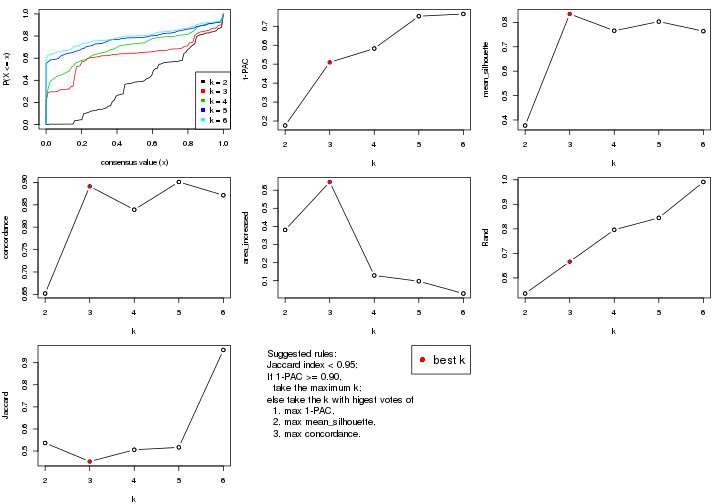
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.176 0.377 0.652 0.3804 0.537 0.537
#> 3 3 0.510 0.834 0.891 0.6456 0.666 0.453
#> 4 4 0.583 0.766 0.839 0.1286 0.796 0.506
#> 5 5 0.753 0.803 0.901 0.0968 0.845 0.517
#> 6 6 0.765 0.764 0.871 0.0289 0.991 0.958
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.9896 0.753 0.440 0.560
#> GSM907859 1 0.9754 -0.471 0.592 0.408
#> GSM907860 2 0.9896 0.753 0.440 0.560
#> GSM907854 2 0.9896 0.753 0.440 0.560
#> GSM907855 2 0.9896 0.753 0.440 0.560
#> GSM907856 2 0.9896 0.753 0.440 0.560
#> GSM907857 2 0.9896 0.753 0.440 0.560
#> GSM907825 2 0.9998 0.610 0.492 0.508
#> GSM907828 1 0.9833 -0.498 0.576 0.424
#> GSM907832 2 0.9608 0.653 0.384 0.616
#> GSM907833 2 0.9608 0.653 0.384 0.616
#> GSM907834 1 0.9933 -0.579 0.548 0.452
#> GSM907826 2 0.9608 0.653 0.384 0.616
#> GSM907827 2 0.9896 0.753 0.440 0.560
#> GSM907829 1 0.3274 0.517 0.940 0.060
#> GSM907830 1 0.9732 -0.462 0.596 0.404
#> GSM907831 2 0.9983 0.704 0.476 0.524
#> GSM907792 1 0.7745 0.522 0.772 0.228
#> GSM907795 1 0.7745 0.522 0.772 0.228
#> GSM907801 1 0.7745 0.522 0.772 0.228
#> GSM907802 1 0.0000 0.565 1.000 0.000
#> GSM907804 1 0.0376 0.566 0.996 0.004
#> GSM907805 1 0.6048 0.543 0.852 0.148
#> GSM907806 1 0.0000 0.565 1.000 0.000
#> GSM907793 1 0.7745 0.522 0.772 0.228
#> GSM907794 1 0.0000 0.565 1.000 0.000
#> GSM907796 1 0.0000 0.565 1.000 0.000
#> GSM907797 1 0.6247 0.401 0.844 0.156
#> GSM907798 1 0.0376 0.563 0.996 0.004
#> GSM907799 1 0.7745 0.522 0.772 0.228
#> GSM907800 1 0.0000 0.565 1.000 0.000
#> GSM907803 1 0.7745 0.522 0.772 0.228
#> GSM907864 1 0.9732 -0.462 0.596 0.404
#> GSM907865 1 0.9754 -0.471 0.592 0.408
#> GSM907868 2 0.9896 0.753 0.440 0.560
#> GSM907869 2 0.9896 0.753 0.440 0.560
#> GSM907870 1 0.9881 -0.519 0.564 0.436
#> GSM907861 2 0.9896 0.753 0.440 0.560
#> GSM907862 2 0.9896 0.753 0.440 0.560
#> GSM907863 2 0.9909 0.748 0.444 0.556
#> GSM907866 2 0.9896 0.753 0.440 0.560
#> GSM907867 2 0.9896 0.753 0.440 0.560
#> GSM907839 1 0.9732 -0.462 0.596 0.404
#> GSM907840 1 0.9732 -0.462 0.596 0.404
#> GSM907842 1 0.9732 -0.462 0.596 0.404
#> GSM907843 1 0.9732 -0.462 0.596 0.404
#> GSM907845 1 0.9815 -0.505 0.580 0.420
#> GSM907846 1 0.9661 -0.443 0.608 0.392
#> GSM907848 2 0.9608 0.653 0.384 0.616
#> GSM907851 1 0.9732 -0.462 0.596 0.404
#> GSM907835 2 0.9608 0.653 0.384 0.616
#> GSM907836 2 0.9635 0.654 0.388 0.612
#> GSM907837 1 0.9866 -0.512 0.568 0.432
#> GSM907838 1 0.9896 -0.526 0.560 0.440
#> GSM907841 2 0.9896 0.753 0.440 0.560
#> GSM907844 2 0.8081 0.622 0.248 0.752
#> GSM907847 2 0.9608 0.653 0.384 0.616
#> GSM907849 1 0.9732 -0.462 0.596 0.404
#> GSM907850 2 0.9608 0.653 0.384 0.616
#> GSM907852 2 0.9732 0.654 0.404 0.596
#> GSM907853 2 0.9795 0.652 0.416 0.584
#> GSM907807 1 0.7745 0.522 0.772 0.228
#> GSM907813 1 0.0000 0.565 1.000 0.000
#> GSM907814 1 0.0000 0.565 1.000 0.000
#> GSM907816 1 0.7745 0.522 0.772 0.228
#> GSM907818 1 0.0000 0.565 1.000 0.000
#> GSM907819 1 0.0000 0.565 1.000 0.000
#> GSM907820 1 0.0000 0.565 1.000 0.000
#> GSM907822 1 0.7745 0.522 0.772 0.228
#> GSM907823 1 0.7745 0.522 0.772 0.228
#> GSM907808 1 0.7745 0.522 0.772 0.228
#> GSM907809 1 0.6048 0.543 0.852 0.148
#> GSM907810 1 0.7745 0.522 0.772 0.228
#> GSM907811 1 0.2423 0.562 0.960 0.040
#> GSM907812 1 0.0000 0.565 1.000 0.000
#> GSM907815 1 0.6247 0.401 0.844 0.156
#> GSM907817 1 0.0000 0.565 1.000 0.000
#> GSM907821 1 0.0000 0.565 1.000 0.000
#> GSM907824 1 0.0000 0.565 1.000 0.000
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907859 2 0.6168 0.462 0.000 0.588 0.412
#> GSM907860 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907854 3 0.2261 0.878 0.000 0.068 0.932
#> GSM907855 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907856 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907857 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907825 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907828 2 0.4062 0.841 0.000 0.836 0.164
#> GSM907832 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907834 2 0.4002 0.842 0.000 0.840 0.160
#> GSM907826 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907827 3 0.4452 0.713 0.000 0.192 0.808
#> GSM907829 1 0.8367 0.615 0.612 0.136 0.252
#> GSM907830 2 0.4555 0.823 0.000 0.800 0.200
#> GSM907831 2 0.4121 0.840 0.000 0.832 0.168
#> GSM907792 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907795 1 0.0237 0.847 0.996 0.000 0.004
#> GSM907801 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907802 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907804 1 0.4062 0.881 0.836 0.000 0.164
#> GSM907805 1 0.3686 0.882 0.860 0.000 0.140
#> GSM907806 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907793 1 0.0237 0.847 0.996 0.000 0.004
#> GSM907794 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907796 1 0.4062 0.881 0.836 0.000 0.164
#> GSM907797 1 0.5815 0.728 0.692 0.004 0.304
#> GSM907798 1 0.4062 0.881 0.836 0.000 0.164
#> GSM907799 1 0.0237 0.847 0.996 0.000 0.004
#> GSM907800 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907803 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907864 2 0.4555 0.823 0.000 0.800 0.200
#> GSM907865 3 0.3192 0.839 0.000 0.112 0.888
#> GSM907868 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907869 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907870 2 0.4062 0.841 0.000 0.836 0.164
#> GSM907861 3 0.5968 0.300 0.000 0.364 0.636
#> GSM907862 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907863 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907866 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907867 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907839 2 0.4555 0.823 0.000 0.800 0.200
#> GSM907840 3 0.4346 0.746 0.000 0.184 0.816
#> GSM907842 2 0.4555 0.823 0.000 0.800 0.200
#> GSM907843 2 0.4062 0.841 0.000 0.836 0.164
#> GSM907845 2 0.7065 0.724 0.072 0.700 0.228
#> GSM907846 2 0.4974 0.795 0.000 0.764 0.236
#> GSM907848 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907851 2 0.5875 0.800 0.056 0.784 0.160
#> GSM907835 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907836 2 0.0424 0.837 0.000 0.992 0.008
#> GSM907837 2 0.4931 0.798 0.000 0.768 0.232
#> GSM907838 2 0.4931 0.798 0.000 0.768 0.232
#> GSM907841 3 0.0000 0.930 0.000 0.000 1.000
#> GSM907844 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907849 2 0.4002 0.842 0.000 0.840 0.160
#> GSM907850 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.835 0.000 1.000 0.000
#> GSM907853 2 0.0747 0.830 0.000 0.984 0.016
#> GSM907807 1 0.0237 0.847 0.996 0.000 0.004
#> GSM907813 1 0.4555 0.852 0.800 0.000 0.200
#> GSM907814 1 0.4555 0.852 0.800 0.000 0.200
#> GSM907816 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907818 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907819 1 0.4062 0.881 0.836 0.000 0.164
#> GSM907820 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907822 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907808 1 0.0237 0.847 0.996 0.000 0.004
#> GSM907809 1 0.3619 0.882 0.864 0.000 0.136
#> GSM907810 1 0.0000 0.845 1.000 0.000 0.000
#> GSM907811 1 0.2590 0.868 0.924 0.004 0.072
#> GSM907812 1 0.4062 0.881 0.836 0.000 0.164
#> GSM907815 1 0.6813 0.373 0.520 0.012 0.468
#> GSM907817 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907821 1 0.4233 0.882 0.836 0.004 0.160
#> GSM907824 1 0.4233 0.882 0.836 0.004 0.160
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907859 3 0.5915 0.6600 0.004 0.036 0.592 0.368
#> GSM907860 3 0.2773 0.7288 0.000 0.116 0.880 0.004
#> GSM907854 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907855 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907856 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907857 3 0.0707 0.7381 0.000 0.000 0.980 0.020
#> GSM907825 2 0.0592 0.8823 0.000 0.984 0.016 0.000
#> GSM907828 2 0.3937 0.7798 0.000 0.800 0.188 0.012
#> GSM907832 2 0.0000 0.8842 0.000 1.000 0.000 0.000
#> GSM907833 2 0.0188 0.8849 0.000 0.996 0.004 0.000
#> GSM907834 2 0.2408 0.8703 0.000 0.896 0.104 0.000
#> GSM907826 2 0.0469 0.8846 0.000 0.988 0.012 0.000
#> GSM907827 3 0.4222 0.6271 0.000 0.272 0.728 0.000
#> GSM907829 2 0.7139 0.3347 0.164 0.628 0.024 0.184
#> GSM907830 3 0.5337 0.3851 0.000 0.424 0.564 0.012
#> GSM907831 2 0.2647 0.8660 0.000 0.880 0.120 0.000
#> GSM907792 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907802 4 0.7265 0.7987 0.236 0.156 0.016 0.592
#> GSM907804 1 0.3674 0.7489 0.852 0.000 0.104 0.044
#> GSM907805 1 0.0895 0.9100 0.976 0.000 0.004 0.020
#> GSM907806 1 0.4161 0.7588 0.832 0.004 0.056 0.108
#> GSM907793 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907794 4 0.5595 0.5958 0.404 0.008 0.012 0.576
#> GSM907796 1 0.3852 0.7440 0.808 0.000 0.012 0.180
#> GSM907797 3 0.7272 0.0823 0.344 0.000 0.496 0.160
#> GSM907798 1 0.3895 0.7406 0.804 0.000 0.012 0.184
#> GSM907799 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907800 4 0.6719 0.7281 0.336 0.056 0.024 0.584
#> GSM907803 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907864 3 0.6282 0.6521 0.004 0.056 0.572 0.368
#> GSM907865 3 0.5832 0.6584 0.004 0.032 0.596 0.368
#> GSM907868 3 0.0336 0.7432 0.000 0.008 0.992 0.000
#> GSM907869 3 0.0707 0.7381 0.000 0.000 0.980 0.020
#> GSM907870 2 0.3428 0.8411 0.000 0.844 0.144 0.012
#> GSM907861 3 0.4356 0.6052 0.000 0.292 0.708 0.000
#> GSM907862 3 0.4535 0.6571 0.000 0.240 0.744 0.016
#> GSM907863 3 0.4535 0.6571 0.000 0.240 0.744 0.016
#> GSM907866 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907867 3 0.3907 0.6678 0.000 0.232 0.768 0.000
#> GSM907839 3 0.6282 0.6521 0.004 0.056 0.572 0.368
#> GSM907840 3 0.5915 0.6589 0.004 0.036 0.592 0.368
#> GSM907842 3 0.6335 0.4803 0.004 0.364 0.572 0.060
#> GSM907843 2 0.3324 0.8481 0.000 0.852 0.136 0.012
#> GSM907845 2 0.3662 0.7790 0.004 0.836 0.012 0.148
#> GSM907846 2 0.3024 0.8483 0.000 0.852 0.148 0.000
#> GSM907848 2 0.0336 0.8851 0.000 0.992 0.008 0.000
#> GSM907851 2 0.4007 0.8471 0.012 0.836 0.128 0.024
#> GSM907835 2 0.0469 0.8846 0.000 0.988 0.012 0.000
#> GSM907836 2 0.1022 0.8870 0.000 0.968 0.032 0.000
#> GSM907837 2 0.3479 0.8472 0.000 0.840 0.148 0.012
#> GSM907838 2 0.3428 0.8504 0.000 0.844 0.144 0.012
#> GSM907841 3 0.0188 0.7430 0.000 0.004 0.996 0.000
#> GSM907844 2 0.0592 0.8862 0.000 0.984 0.016 0.000
#> GSM907847 2 0.0000 0.8842 0.000 1.000 0.000 0.000
#> GSM907849 2 0.3217 0.8521 0.000 0.860 0.128 0.012
#> GSM907850 2 0.0000 0.8842 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0336 0.8851 0.000 0.992 0.008 0.000
#> GSM907853 2 0.0000 0.8842 0.000 1.000 0.000 0.000
#> GSM907807 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907813 3 0.7775 0.2531 0.352 0.000 0.404 0.244
#> GSM907814 3 0.7098 0.5482 0.192 0.000 0.564 0.244
#> GSM907816 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907818 4 0.5562 0.6148 0.392 0.008 0.012 0.588
#> GSM907819 1 0.3764 0.7498 0.816 0.000 0.012 0.172
#> GSM907820 4 0.8251 0.6203 0.136 0.256 0.072 0.536
#> GSM907822 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0657 0.9146 0.984 0.000 0.004 0.012
#> GSM907810 1 0.0000 0.9216 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0779 0.9092 0.980 0.004 0.000 0.016
#> GSM907812 1 0.3479 0.7807 0.840 0.000 0.012 0.148
#> GSM907815 3 0.3647 0.6599 0.108 0.000 0.852 0.040
#> GSM907817 4 0.7558 0.7930 0.272 0.120 0.036 0.572
#> GSM907821 4 0.7130 0.8005 0.244 0.148 0.012 0.596
#> GSM907824 4 0.7286 0.7389 0.164 0.228 0.016 0.592
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907859 4 0.0000 0.940 0.000 0.000 0.000 1.000 0.000
#> GSM907860 3 0.4035 0.707 0.000 0.156 0.784 0.060 0.000
#> GSM907854 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907855 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907825 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907828 2 0.2020 0.849 0.000 0.900 0.000 0.100 0.000
#> GSM907832 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907833 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907834 2 0.2732 0.731 0.000 0.840 0.160 0.000 0.000
#> GSM907826 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907827 3 0.4227 0.478 0.000 0.420 0.580 0.000 0.000
#> GSM907829 5 0.3242 0.645 0.000 0.216 0.000 0.000 0.784
#> GSM907830 2 0.3003 0.773 0.000 0.812 0.000 0.188 0.000
#> GSM907831 3 0.4278 0.389 0.000 0.452 0.548 0.000 0.000
#> GSM907792 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.3109 0.739 0.000 0.200 0.000 0.000 0.800
#> GSM907804 5 0.4467 0.550 0.344 0.016 0.000 0.000 0.640
#> GSM907805 1 0.0162 0.956 0.996 0.000 0.000 0.000 0.004
#> GSM907806 5 0.4218 0.571 0.332 0.008 0.000 0.000 0.660
#> GSM907793 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.0510 0.765 0.016 0.000 0.000 0.000 0.984
#> GSM907796 5 0.1608 0.762 0.072 0.000 0.000 0.000 0.928
#> GSM907797 5 0.1608 0.741 0.000 0.000 0.000 0.072 0.928
#> GSM907798 5 0.1608 0.762 0.072 0.000 0.000 0.000 0.928
#> GSM907799 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.2891 0.752 0.000 0.176 0.000 0.000 0.824
#> GSM907803 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.940 0.000 0.000 0.000 1.000 0.000
#> GSM907865 4 0.0000 0.940 0.000 0.000 0.000 1.000 0.000
#> GSM907868 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907869 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907870 2 0.1851 0.860 0.000 0.912 0.000 0.088 0.000
#> GSM907861 3 0.3999 0.602 0.000 0.344 0.656 0.000 0.000
#> GSM907862 3 0.5404 0.622 0.000 0.264 0.636 0.100 0.000
#> GSM907863 3 0.5644 0.557 0.000 0.316 0.584 0.100 0.000
#> GSM907866 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.3612 0.686 0.000 0.268 0.732 0.000 0.000
#> GSM907839 4 0.0000 0.940 0.000 0.000 0.000 1.000 0.000
#> GSM907840 4 0.0000 0.940 0.000 0.000 0.000 1.000 0.000
#> GSM907842 4 0.3305 0.674 0.000 0.224 0.000 0.776 0.000
#> GSM907843 2 0.3395 0.721 0.000 0.764 0.000 0.236 0.000
#> GSM907845 2 0.3561 0.575 0.000 0.740 0.000 0.000 0.260
#> GSM907846 2 0.2329 0.806 0.000 0.876 0.000 0.000 0.124
#> GSM907848 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907851 2 0.4708 0.607 0.000 0.712 0.000 0.068 0.220
#> GSM907835 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907837 2 0.0609 0.903 0.000 0.980 0.000 0.020 0.000
#> GSM907838 2 0.1341 0.883 0.000 0.944 0.000 0.056 0.000
#> GSM907841 3 0.0000 0.776 0.000 0.000 1.000 0.000 0.000
#> GSM907844 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907847 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907849 2 0.3152 0.822 0.000 0.840 0.000 0.136 0.024
#> GSM907850 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.0000 0.911 0.000 1.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.2690 0.802 0.844 0.000 0.000 0.156 0.000
#> GSM907814 1 0.1908 0.872 0.908 0.000 0.000 0.092 0.000
#> GSM907816 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.0000 0.761 0.000 0.000 0.000 0.000 1.000
#> GSM907819 5 0.1608 0.762 0.072 0.000 0.000 0.000 0.928
#> GSM907820 5 0.4030 0.506 0.000 0.352 0.000 0.000 0.648
#> GSM907822 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.959 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.0404 0.949 0.988 0.000 0.000 0.000 0.012
#> GSM907812 1 0.4101 0.432 0.628 0.000 0.000 0.000 0.372
#> GSM907815 5 0.5074 0.547 0.000 0.000 0.268 0.072 0.660
#> GSM907817 5 0.3242 0.725 0.000 0.216 0.000 0.000 0.784
#> GSM907821 5 0.2127 0.769 0.000 0.108 0.000 0.000 0.892
#> GSM907824 5 0.3039 0.745 0.000 0.192 0.000 0.000 0.808
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907859 4 0.0000 0.881 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907860 3 0.3023 0.738 0.000 0.044 0.836 0.000 0.000 0.120
#> GSM907854 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907855 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907856 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907857 3 0.1714 0.748 0.000 0.000 0.908 0.000 0.000 0.092
#> GSM907825 2 0.0260 0.873 0.000 0.992 0.000 0.000 0.008 0.000
#> GSM907828 2 0.2593 0.808 0.000 0.844 0.000 0.008 0.000 0.148
#> GSM907832 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907833 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907834 2 0.2762 0.637 0.000 0.804 0.196 0.000 0.000 0.000
#> GSM907826 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907827 3 0.4199 0.530 0.000 0.380 0.600 0.000 0.000 0.020
#> GSM907829 5 0.4362 0.196 0.000 0.388 0.000 0.000 0.584 0.028
#> GSM907830 2 0.3101 0.794 0.000 0.820 0.000 0.032 0.000 0.148
#> GSM907831 3 0.3810 0.455 0.000 0.428 0.572 0.000 0.000 0.000
#> GSM907792 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.2340 0.757 0.000 0.148 0.000 0.000 0.852 0.000
#> GSM907804 5 0.3101 0.580 0.244 0.000 0.000 0.000 0.756 0.000
#> GSM907805 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907806 5 0.2793 0.628 0.200 0.000 0.000 0.000 0.800 0.000
#> GSM907793 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.0260 0.712 0.000 0.008 0.000 0.000 0.992 0.000
#> GSM907796 5 0.3109 0.502 0.004 0.000 0.000 0.000 0.772 0.224
#> GSM907797 6 0.2378 0.918 0.000 0.000 0.000 0.000 0.152 0.848
#> GSM907798 5 0.3713 0.467 0.032 0.000 0.000 0.000 0.744 0.224
#> GSM907799 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.2340 0.757 0.000 0.148 0.000 0.000 0.852 0.000
#> GSM907803 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.881 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0000 0.881 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907869 3 0.1714 0.748 0.000 0.000 0.908 0.000 0.000 0.092
#> GSM907870 2 0.2593 0.808 0.000 0.844 0.000 0.008 0.000 0.148
#> GSM907861 3 0.3175 0.660 0.000 0.256 0.744 0.000 0.000 0.000
#> GSM907862 3 0.4974 0.625 0.000 0.172 0.672 0.008 0.000 0.148
#> GSM907863 3 0.5425 0.554 0.000 0.244 0.600 0.008 0.000 0.148
#> GSM907866 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907867 3 0.2509 0.765 0.000 0.088 0.876 0.000 0.000 0.036
#> GSM907839 4 0.0000 0.881 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907840 4 0.0000 0.881 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.5079 0.386 0.000 0.224 0.000 0.628 0.000 0.148
#> GSM907843 2 0.4273 0.714 0.000 0.732 0.000 0.120 0.000 0.148
#> GSM907845 2 0.3151 0.571 0.000 0.748 0.000 0.000 0.252 0.000
#> GSM907846 2 0.0790 0.860 0.000 0.968 0.000 0.000 0.032 0.000
#> GSM907848 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907851 2 0.5849 0.147 0.000 0.448 0.000 0.008 0.396 0.148
#> GSM907835 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907836 2 0.0146 0.877 0.000 0.996 0.000 0.000 0.000 0.004
#> GSM907837 2 0.2340 0.812 0.000 0.852 0.000 0.000 0.000 0.148
#> GSM907838 2 0.2482 0.810 0.000 0.848 0.000 0.004 0.000 0.148
#> GSM907841 3 0.0000 0.795 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907844 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907847 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907849 2 0.4818 0.708 0.000 0.704 0.000 0.016 0.132 0.148
#> GSM907850 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907853 2 0.0000 0.878 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.2762 0.732 0.804 0.000 0.000 0.196 0.000 0.000
#> GSM907814 1 0.1957 0.828 0.888 0.000 0.000 0.112 0.000 0.000
#> GSM907816 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.0000 0.705 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907819 5 0.2006 0.644 0.004 0.000 0.000 0.000 0.892 0.104
#> GSM907820 5 0.2823 0.701 0.000 0.204 0.000 0.000 0.796 0.000
#> GSM907822 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.926 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.3684 0.324 0.628 0.000 0.000 0.000 0.372 0.000
#> GSM907812 1 0.5201 0.365 0.616 0.000 0.000 0.000 0.200 0.184
#> GSM907815 6 0.2875 0.917 0.000 0.000 0.052 0.000 0.096 0.852
#> GSM907817 5 0.2340 0.757 0.000 0.148 0.000 0.000 0.852 0.000
#> GSM907821 5 0.2340 0.757 0.000 0.148 0.000 0.000 0.852 0.000
#> GSM907824 5 0.2340 0.757 0.000 0.148 0.000 0.000 0.852 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
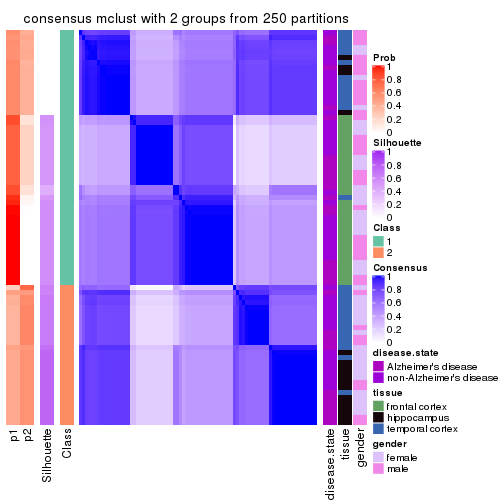
consensus_heatmap(res, k = 3)
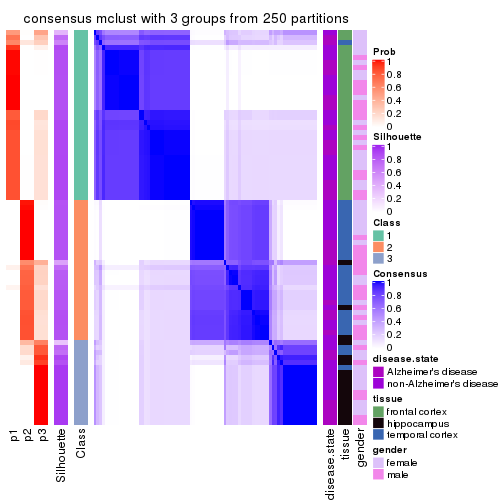
consensus_heatmap(res, k = 4)
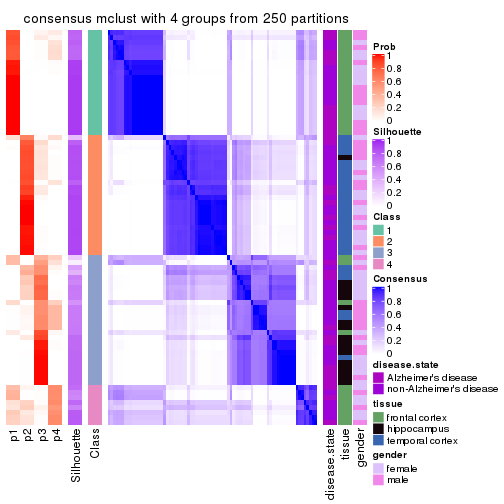
consensus_heatmap(res, k = 5)
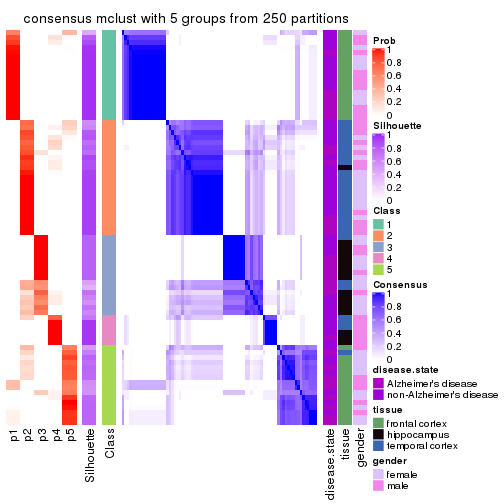
consensus_heatmap(res, k = 6)
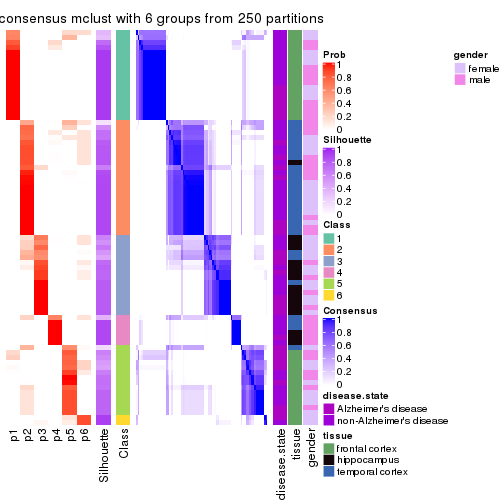
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
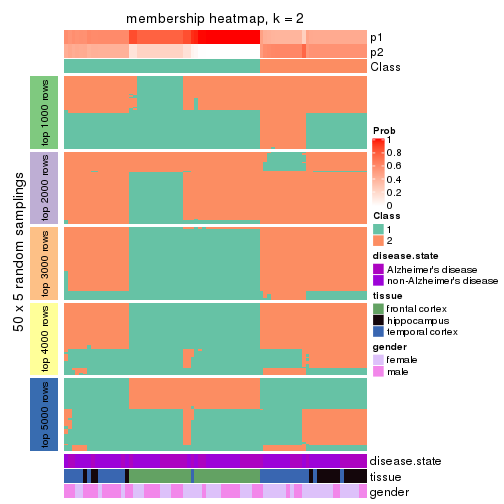
membership_heatmap(res, k = 3)
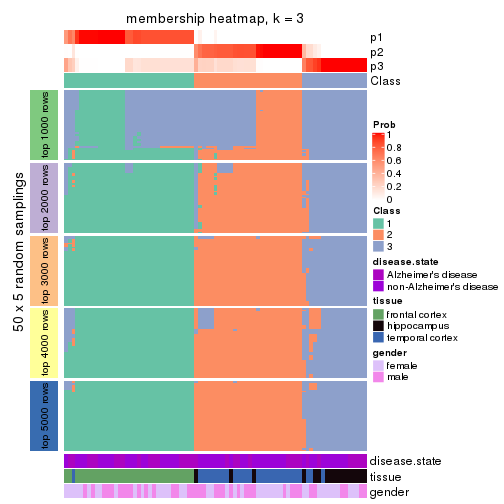
membership_heatmap(res, k = 4)
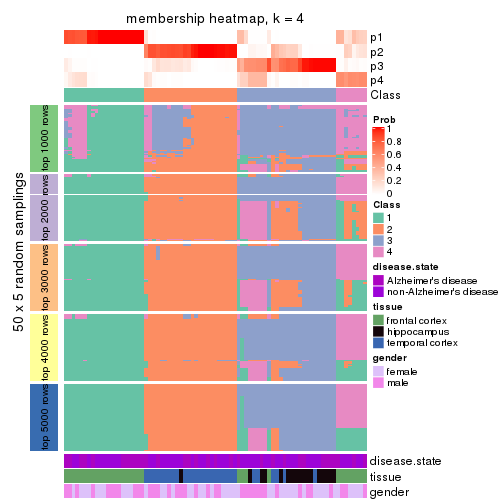
membership_heatmap(res, k = 5)
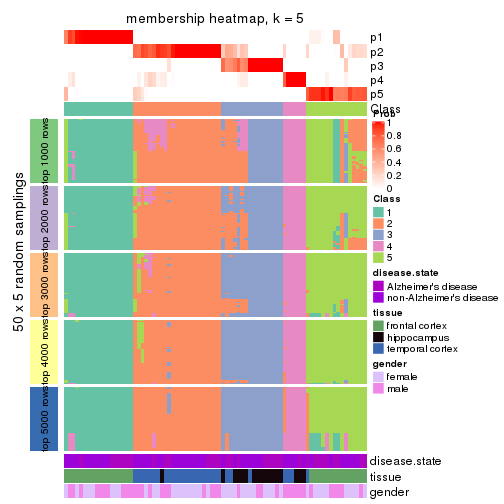
membership_heatmap(res, k = 6)
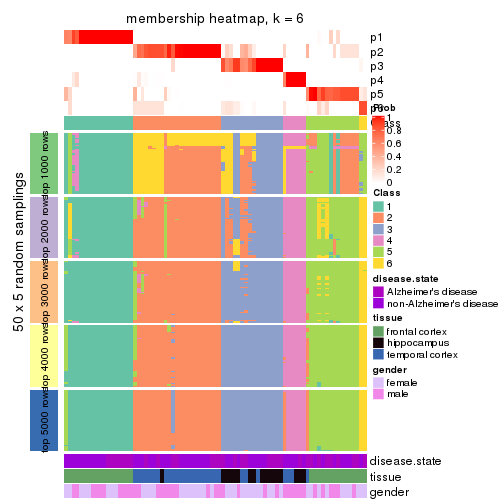
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
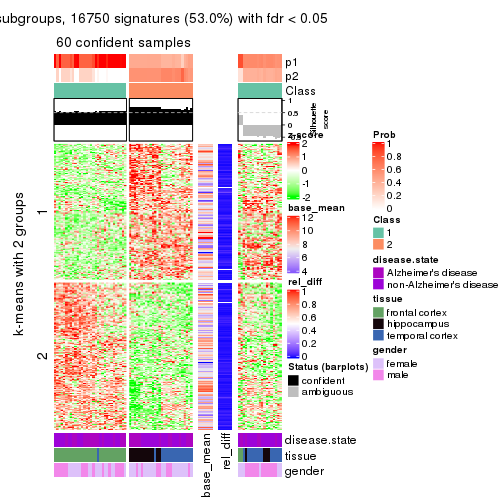
get_signatures(res, k = 3)
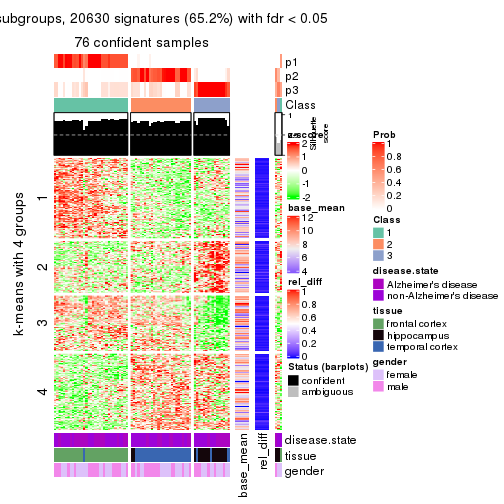
get_signatures(res, k = 4)
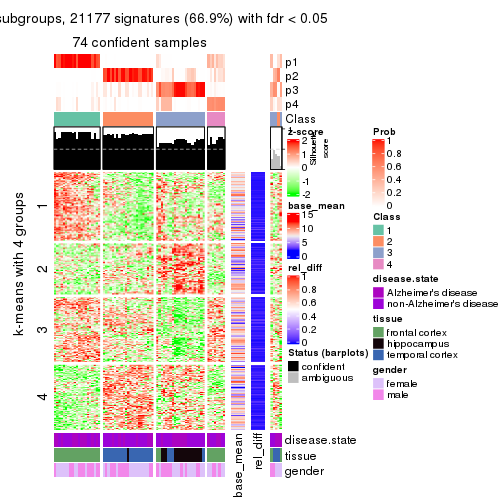
get_signatures(res, k = 5)
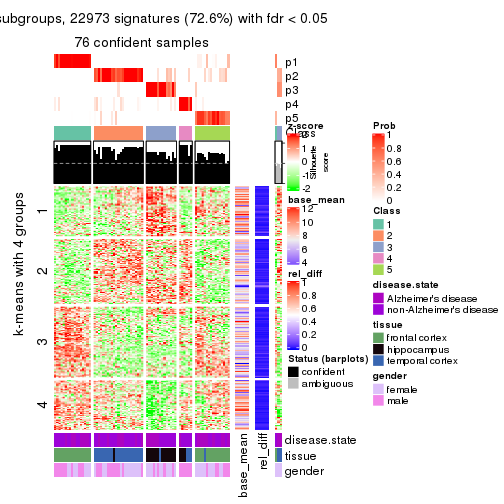
get_signatures(res, k = 6)
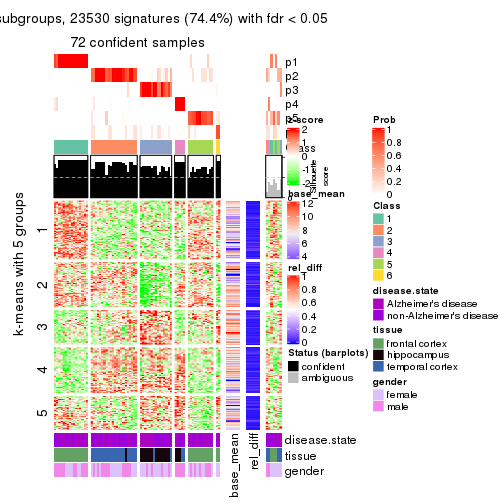
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
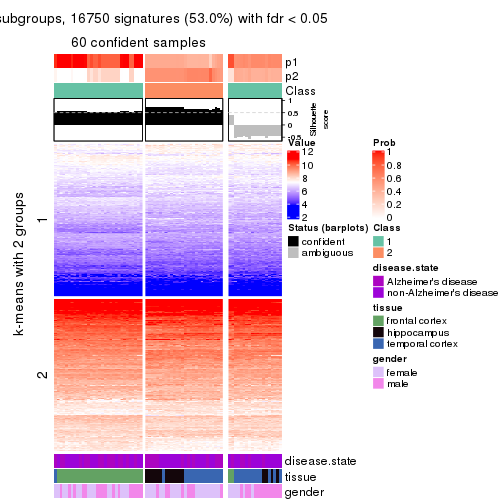
get_signatures(res, k = 3, scale_rows = FALSE)
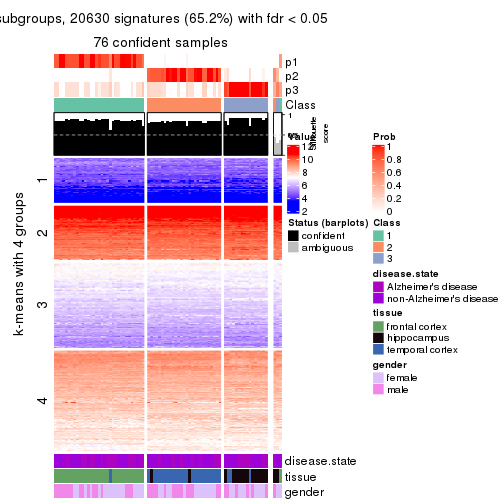
get_signatures(res, k = 4, scale_rows = FALSE)
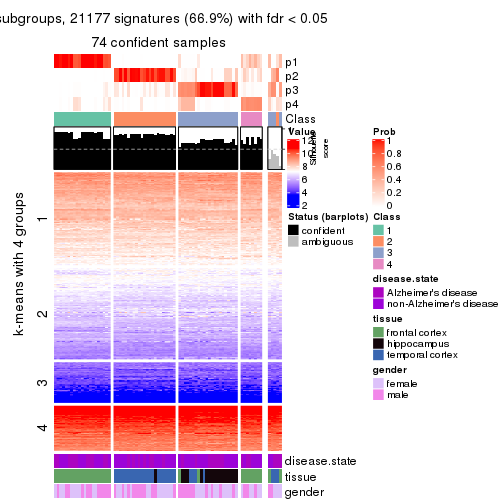
get_signatures(res, k = 5, scale_rows = FALSE)
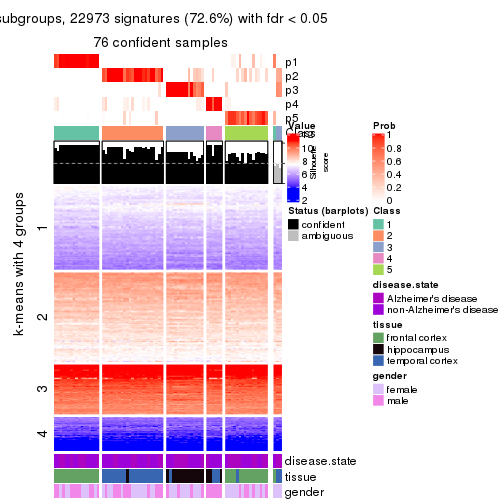
get_signatures(res, k = 6, scale_rows = FALSE)
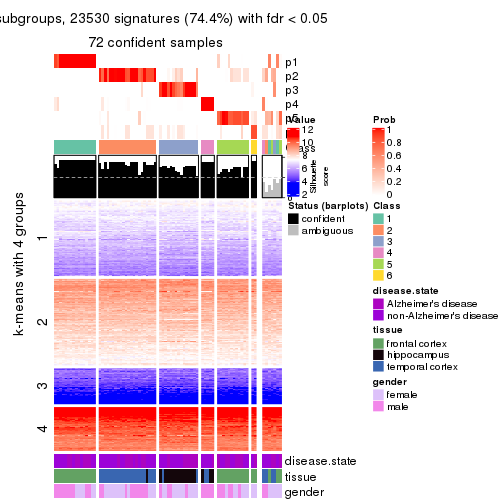
Compare the overlap of signatures from different k:
compare_signatures(res)
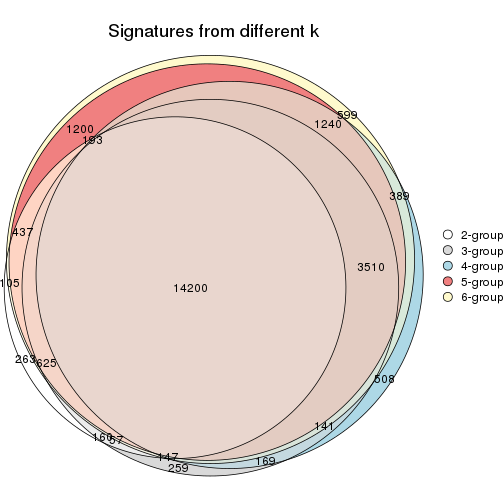
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
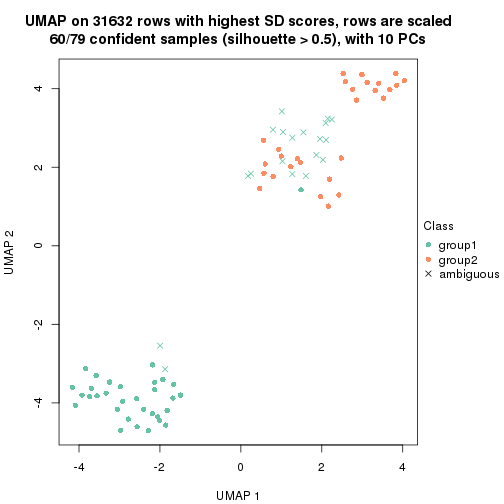
dimension_reduction(res, k = 3, method = "UMAP")
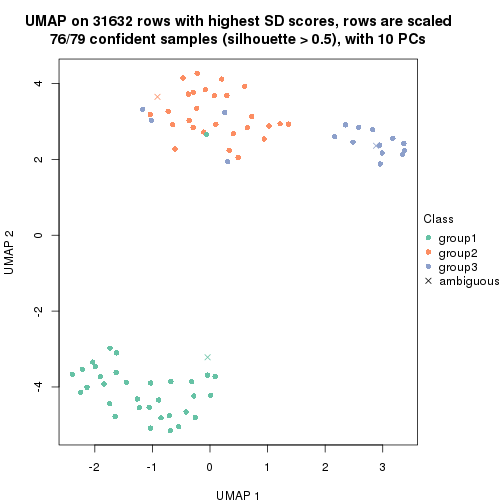
dimension_reduction(res, k = 4, method = "UMAP")
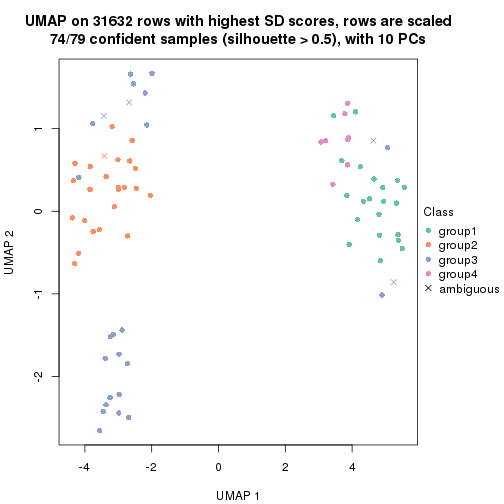
dimension_reduction(res, k = 5, method = "UMAP")
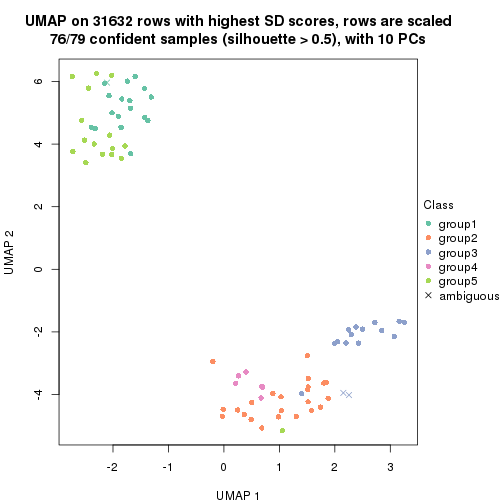
dimension_reduction(res, k = 6, method = "UMAP")
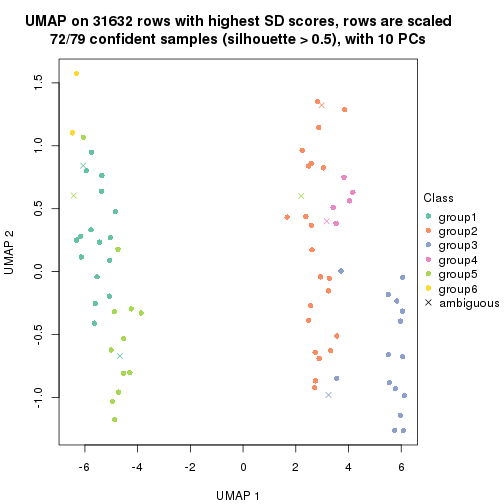
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
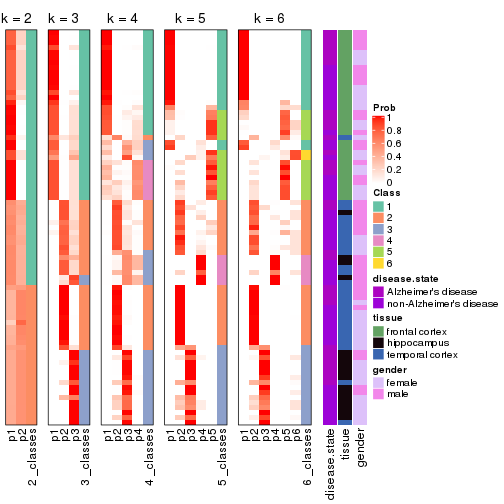
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:mclust 60 0.959 6.15e-13 0.1538 2
#> SD:mclust 76 0.323 9.33e-24 0.6508 3
#> SD:mclust 74 0.502 4.27e-21 0.9059 4
#> SD:mclust 76 0.397 1.02e-22 0.0388 5
#> SD:mclust 72 0.792 2.80e-20 0.0440 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["SD", "NMF"]
# you can also extract it by
# res = res_list["SD:NMF"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'SD' method.
#> Subgroups are detected by 'NMF' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
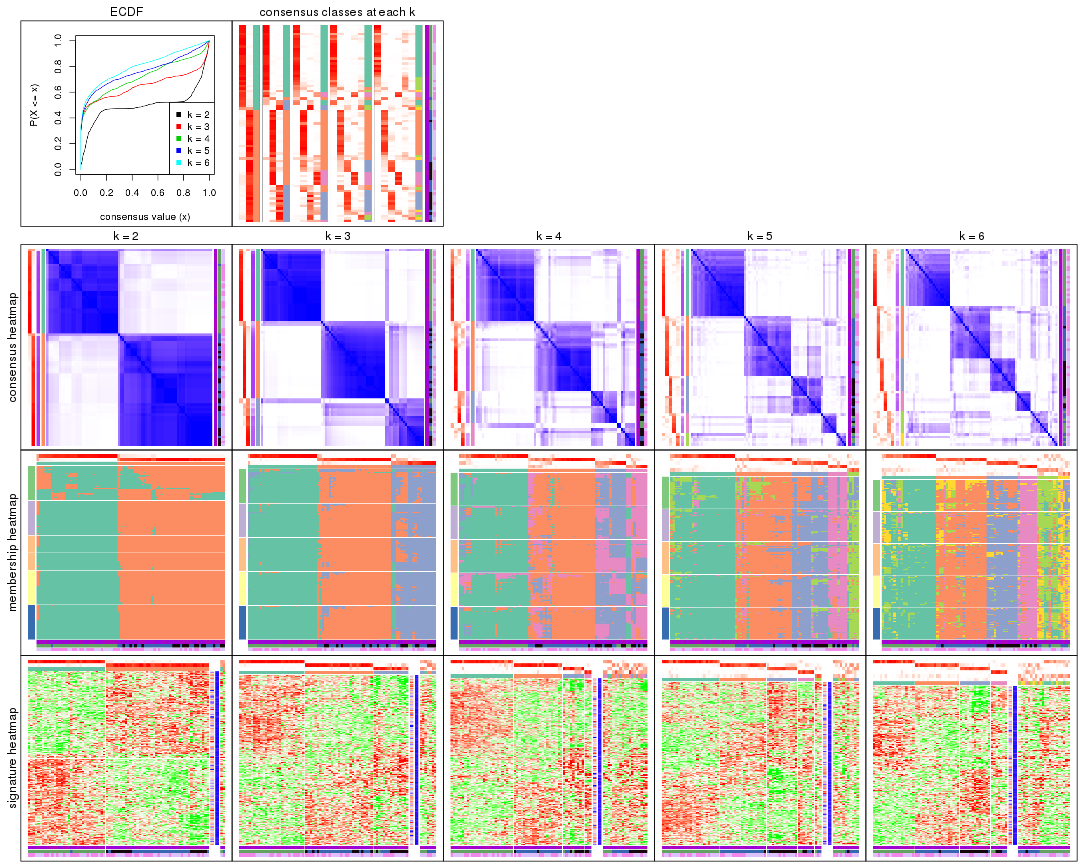
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
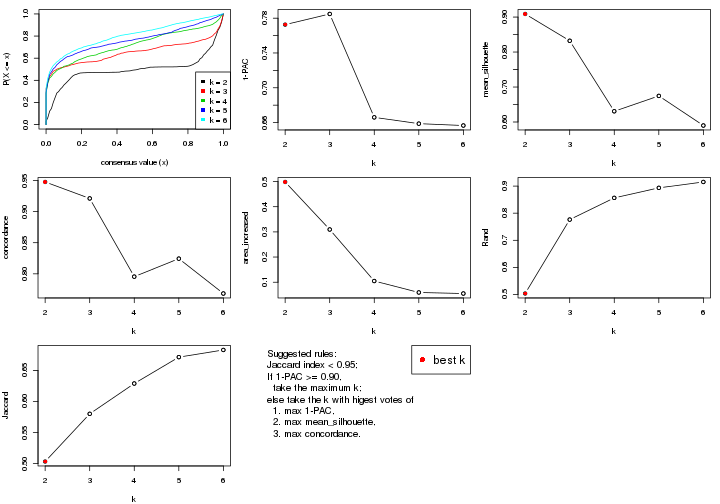
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.773 0.909 0.948 0.4983 0.503 0.503
#> 3 3 0.785 0.832 0.921 0.3095 0.776 0.580
#> 4 4 0.666 0.631 0.795 0.1047 0.857 0.629
#> 5 5 0.659 0.675 0.824 0.0592 0.894 0.671
#> 6 6 0.657 0.590 0.768 0.0551 0.915 0.683
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.1633 0.9408 0.024 0.976
#> GSM907859 2 0.2603 0.9298 0.044 0.956
#> GSM907860 2 0.0000 0.9422 0.000 1.000
#> GSM907854 2 0.2948 0.9328 0.052 0.948
#> GSM907855 2 0.0000 0.9422 0.000 1.000
#> GSM907856 2 0.0000 0.9422 0.000 1.000
#> GSM907857 2 0.2948 0.9328 0.052 0.948
#> GSM907825 2 0.2948 0.9328 0.052 0.948
#> GSM907828 2 0.3431 0.9193 0.064 0.936
#> GSM907832 2 0.2236 0.9389 0.036 0.964
#> GSM907833 2 0.0000 0.9422 0.000 1.000
#> GSM907834 2 0.2948 0.9328 0.052 0.948
#> GSM907826 2 0.2603 0.9360 0.044 0.956
#> GSM907827 2 0.0376 0.9422 0.004 0.996
#> GSM907829 2 0.5842 0.8571 0.140 0.860
#> GSM907830 2 0.3114 0.9242 0.056 0.944
#> GSM907831 2 0.2603 0.9360 0.044 0.956
#> GSM907792 1 0.0672 0.9490 0.992 0.008
#> GSM907795 1 0.0672 0.9490 0.992 0.008
#> GSM907801 1 0.0938 0.9483 0.988 0.012
#> GSM907802 1 0.2948 0.9295 0.948 0.052
#> GSM907804 1 0.0938 0.9483 0.988 0.012
#> GSM907805 1 0.0000 0.9493 1.000 0.000
#> GSM907806 1 0.0000 0.9493 1.000 0.000
#> GSM907793 1 0.0000 0.9493 1.000 0.000
#> GSM907794 1 0.2603 0.9346 0.956 0.044
#> GSM907796 1 0.4815 0.8894 0.896 0.104
#> GSM907797 1 0.5408 0.8708 0.876 0.124
#> GSM907798 1 0.4431 0.8998 0.908 0.092
#> GSM907799 1 0.0000 0.9493 1.000 0.000
#> GSM907800 1 0.0000 0.9493 1.000 0.000
#> GSM907803 1 0.0000 0.9493 1.000 0.000
#> GSM907864 2 0.5737 0.8648 0.136 0.864
#> GSM907865 2 0.5178 0.8827 0.116 0.884
#> GSM907868 2 0.1184 0.9421 0.016 0.984
#> GSM907869 2 0.2948 0.9328 0.052 0.948
#> GSM907870 2 0.4298 0.9034 0.088 0.912
#> GSM907861 2 0.2603 0.9360 0.044 0.956
#> GSM907862 2 0.0000 0.9422 0.000 1.000
#> GSM907863 2 0.0000 0.9422 0.000 1.000
#> GSM907866 2 0.2603 0.9360 0.044 0.956
#> GSM907867 2 0.0000 0.9422 0.000 1.000
#> GSM907839 2 0.5737 0.8648 0.136 0.864
#> GSM907840 2 0.5178 0.8827 0.116 0.884
#> GSM907842 2 0.5059 0.8861 0.112 0.888
#> GSM907843 2 0.3879 0.9118 0.076 0.924
#> GSM907845 2 0.5294 0.8794 0.120 0.880
#> GSM907846 2 0.9795 0.2264 0.416 0.584
#> GSM907848 2 0.0672 0.9410 0.008 0.992
#> GSM907851 1 0.3733 0.9146 0.928 0.072
#> GSM907835 2 0.1414 0.9417 0.020 0.980
#> GSM907836 2 0.0000 0.9422 0.000 1.000
#> GSM907837 2 0.2043 0.9340 0.032 0.968
#> GSM907838 2 0.1633 0.9367 0.024 0.976
#> GSM907841 2 0.2043 0.9394 0.032 0.968
#> GSM907844 2 0.0376 0.9424 0.004 0.996
#> GSM907847 2 0.0000 0.9422 0.000 1.000
#> GSM907849 2 0.5946 0.8607 0.144 0.856
#> GSM907850 2 0.0000 0.9422 0.000 1.000
#> GSM907852 2 0.0938 0.9429 0.012 0.988
#> GSM907853 2 0.2948 0.9328 0.052 0.948
#> GSM907807 1 0.0000 0.9493 1.000 0.000
#> GSM907813 1 0.2948 0.9268 0.948 0.052
#> GSM907814 1 0.2778 0.9295 0.952 0.048
#> GSM907816 1 0.2236 0.9370 0.964 0.036
#> GSM907818 1 0.2603 0.9344 0.956 0.044
#> GSM907819 1 0.1843 0.9419 0.972 0.028
#> GSM907820 1 0.0938 0.9483 0.988 0.012
#> GSM907822 1 0.2603 0.9319 0.956 0.044
#> GSM907823 1 0.2236 0.9370 0.964 0.036
#> GSM907808 1 0.0000 0.9493 1.000 0.000
#> GSM907809 1 0.0672 0.9482 0.992 0.008
#> GSM907810 1 0.0938 0.9483 0.988 0.012
#> GSM907811 1 0.1184 0.9469 0.984 0.016
#> GSM907812 1 0.2043 0.9400 0.968 0.032
#> GSM907815 1 0.9983 0.0959 0.524 0.476
#> GSM907817 1 0.0672 0.9488 0.992 0.008
#> GSM907821 1 0.5629 0.8621 0.868 0.132
#> GSM907824 1 0.4431 0.9001 0.908 0.092
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.3116 0.773 0.000 0.108 0.892
#> GSM907859 2 0.0237 0.918 0.000 0.996 0.004
#> GSM907860 2 0.3340 0.839 0.000 0.880 0.120
#> GSM907854 3 0.0592 0.797 0.000 0.012 0.988
#> GSM907855 3 0.5948 0.500 0.000 0.360 0.640
#> GSM907856 3 0.5591 0.594 0.000 0.304 0.696
#> GSM907857 3 0.0237 0.796 0.000 0.004 0.996
#> GSM907825 3 0.2261 0.789 0.000 0.068 0.932
#> GSM907828 2 0.0237 0.918 0.000 0.996 0.004
#> GSM907832 2 0.2537 0.885 0.000 0.920 0.080
#> GSM907833 2 0.0592 0.917 0.000 0.988 0.012
#> GSM907834 3 0.4121 0.735 0.000 0.168 0.832
#> GSM907826 2 0.2796 0.874 0.000 0.908 0.092
#> GSM907827 2 0.5397 0.572 0.000 0.720 0.280
#> GSM907829 3 0.0592 0.794 0.012 0.000 0.988
#> GSM907830 2 0.0475 0.917 0.004 0.992 0.004
#> GSM907831 3 0.6252 0.272 0.000 0.444 0.556
#> GSM907792 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907802 1 0.0892 0.957 0.980 0.000 0.020
#> GSM907804 1 0.0424 0.962 0.992 0.008 0.000
#> GSM907805 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907806 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907794 1 0.0424 0.963 0.992 0.000 0.008
#> GSM907796 3 0.6192 0.189 0.420 0.000 0.580
#> GSM907797 3 0.1964 0.776 0.056 0.000 0.944
#> GSM907798 3 0.6111 0.257 0.396 0.000 0.604
#> GSM907799 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907800 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907803 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907864 2 0.0424 0.914 0.008 0.992 0.000
#> GSM907865 2 0.0237 0.916 0.004 0.996 0.000
#> GSM907868 3 0.5733 0.564 0.000 0.324 0.676
#> GSM907869 3 0.0237 0.796 0.000 0.004 0.996
#> GSM907870 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907861 3 0.3816 0.751 0.000 0.148 0.852
#> GSM907862 2 0.2261 0.889 0.000 0.932 0.068
#> GSM907863 2 0.1964 0.898 0.000 0.944 0.056
#> GSM907866 3 0.0592 0.797 0.000 0.012 0.988
#> GSM907867 2 0.4504 0.733 0.000 0.804 0.196
#> GSM907839 2 0.0424 0.914 0.008 0.992 0.000
#> GSM907840 2 0.0237 0.916 0.004 0.996 0.000
#> GSM907842 2 0.0237 0.916 0.004 0.996 0.000
#> GSM907843 2 0.0424 0.914 0.008 0.992 0.000
#> GSM907845 3 0.0747 0.793 0.016 0.000 0.984
#> GSM907846 2 0.6742 0.448 0.316 0.656 0.028
#> GSM907848 2 0.0237 0.918 0.000 0.996 0.004
#> GSM907851 2 0.5988 0.400 0.368 0.632 0.000
#> GSM907835 2 0.1529 0.906 0.000 0.960 0.040
#> GSM907836 2 0.1031 0.914 0.000 0.976 0.024
#> GSM907837 2 0.0237 0.918 0.000 0.996 0.004
#> GSM907838 2 0.0424 0.918 0.000 0.992 0.008
#> GSM907841 3 0.6062 0.437 0.000 0.384 0.616
#> GSM907844 2 0.1964 0.898 0.000 0.944 0.056
#> GSM907847 2 0.0747 0.917 0.000 0.984 0.016
#> GSM907849 2 0.0424 0.914 0.008 0.992 0.000
#> GSM907850 2 0.0892 0.915 0.000 0.980 0.020
#> GSM907852 2 0.0747 0.917 0.000 0.984 0.016
#> GSM907853 2 0.4062 0.783 0.000 0.836 0.164
#> GSM907807 1 0.0000 0.965 1.000 0.000 0.000
#> GSM907813 1 0.3482 0.840 0.872 0.128 0.000
#> GSM907814 1 0.1643 0.939 0.956 0.044 0.000
#> GSM907816 1 0.1289 0.949 0.968 0.032 0.000
#> GSM907818 1 0.1289 0.949 0.968 0.000 0.032
#> GSM907819 1 0.1163 0.952 0.972 0.000 0.028
#> GSM907820 1 0.1163 0.952 0.972 0.028 0.000
#> GSM907822 1 0.1411 0.946 0.964 0.036 0.000
#> GSM907823 1 0.1289 0.949 0.968 0.032 0.000
#> GSM907808 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907809 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907810 1 0.0424 0.962 0.992 0.008 0.000
#> GSM907811 1 0.0892 0.957 0.980 0.020 0.000
#> GSM907812 1 0.0892 0.958 0.980 0.000 0.020
#> GSM907815 3 0.1289 0.787 0.032 0.000 0.968
#> GSM907817 1 0.0237 0.964 0.996 0.000 0.004
#> GSM907821 1 0.6154 0.313 0.592 0.000 0.408
#> GSM907824 1 0.1860 0.932 0.948 0.000 0.052
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.4889 0.5503 0.000 0.004 0.636 0.360
#> GSM907859 4 0.0927 0.4892 0.000 0.008 0.016 0.976
#> GSM907860 4 0.6953 -0.0446 0.000 0.412 0.112 0.476
#> GSM907854 3 0.0336 0.6711 0.000 0.008 0.992 0.000
#> GSM907855 4 0.7369 -0.3529 0.000 0.160 0.408 0.432
#> GSM907856 3 0.6709 0.3423 0.000 0.088 0.460 0.452
#> GSM907857 3 0.0000 0.6701 0.000 0.000 1.000 0.000
#> GSM907825 2 0.7276 0.1293 0.104 0.468 0.416 0.012
#> GSM907828 2 0.1557 0.7773 0.000 0.944 0.000 0.056
#> GSM907832 2 0.1271 0.7900 0.012 0.968 0.012 0.008
#> GSM907833 2 0.0188 0.7984 0.000 0.996 0.000 0.004
#> GSM907834 2 0.5368 0.4625 0.008 0.640 0.340 0.012
#> GSM907826 2 0.0336 0.7985 0.000 0.992 0.008 0.000
#> GSM907827 2 0.5998 0.5559 0.000 0.668 0.240 0.092
#> GSM907829 3 0.2870 0.6234 0.036 0.044 0.908 0.012
#> GSM907830 2 0.4985 0.1865 0.000 0.532 0.000 0.468
#> GSM907831 2 0.3448 0.6983 0.000 0.828 0.168 0.004
#> GSM907792 1 0.0657 0.8722 0.984 0.004 0.000 0.012
#> GSM907795 1 0.1022 0.8663 0.968 0.000 0.000 0.032
#> GSM907801 1 0.0188 0.8727 0.996 0.000 0.000 0.004
#> GSM907802 1 0.5938 0.6660 0.720 0.160 0.108 0.012
#> GSM907804 1 0.1637 0.8488 0.940 0.000 0.000 0.060
#> GSM907805 1 0.0592 0.8716 0.984 0.000 0.000 0.016
#> GSM907806 1 0.1182 0.8690 0.968 0.016 0.000 0.016
#> GSM907793 1 0.1118 0.8644 0.964 0.000 0.000 0.036
#> GSM907794 1 0.1953 0.8550 0.940 0.044 0.004 0.012
#> GSM907796 1 0.5441 0.4524 0.588 0.004 0.396 0.012
#> GSM907797 3 0.0469 0.6663 0.012 0.000 0.988 0.000
#> GSM907798 1 0.5038 0.5670 0.652 0.000 0.336 0.012
#> GSM907799 1 0.0336 0.8725 0.992 0.000 0.000 0.008
#> GSM907800 1 0.1854 0.8539 0.940 0.048 0.000 0.012
#> GSM907803 1 0.0657 0.8709 0.984 0.012 0.000 0.004
#> GSM907864 4 0.3074 0.5065 0.000 0.152 0.000 0.848
#> GSM907865 4 0.0657 0.5013 0.004 0.012 0.000 0.984
#> GSM907868 3 0.6058 0.5283 0.000 0.060 0.604 0.336
#> GSM907869 3 0.4992 0.4190 0.000 0.000 0.524 0.476
#> GSM907870 2 0.1022 0.7913 0.000 0.968 0.000 0.032
#> GSM907861 3 0.4304 0.4101 0.000 0.284 0.716 0.000
#> GSM907862 2 0.5403 0.4218 0.000 0.628 0.024 0.348
#> GSM907863 2 0.4284 0.6239 0.000 0.764 0.012 0.224
#> GSM907866 3 0.4585 0.5706 0.000 0.000 0.668 0.332
#> GSM907867 2 0.7205 0.2027 0.000 0.504 0.152 0.344
#> GSM907839 4 0.3266 0.4985 0.000 0.168 0.000 0.832
#> GSM907840 4 0.1211 0.5084 0.000 0.040 0.000 0.960
#> GSM907842 2 0.4804 0.3728 0.000 0.616 0.000 0.384
#> GSM907843 2 0.0817 0.7952 0.000 0.976 0.000 0.024
#> GSM907845 3 0.3367 0.6104 0.040 0.064 0.884 0.012
#> GSM907846 2 0.9624 -0.1780 0.220 0.324 0.136 0.320
#> GSM907848 2 0.0188 0.7977 0.004 0.996 0.000 0.000
#> GSM907851 2 0.4122 0.5327 0.236 0.760 0.000 0.004
#> GSM907835 2 0.0188 0.7977 0.004 0.996 0.000 0.000
#> GSM907836 2 0.0707 0.7965 0.000 0.980 0.000 0.020
#> GSM907837 2 0.0707 0.7965 0.000 0.980 0.000 0.020
#> GSM907838 2 0.0921 0.7934 0.000 0.972 0.000 0.028
#> GSM907841 3 0.5229 0.4847 0.000 0.008 0.564 0.428
#> GSM907844 2 0.0657 0.7985 0.000 0.984 0.004 0.012
#> GSM907847 2 0.0469 0.7954 0.012 0.988 0.000 0.000
#> GSM907849 2 0.0524 0.7990 0.004 0.988 0.000 0.008
#> GSM907850 2 0.0000 0.7982 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0895 0.7908 0.020 0.976 0.000 0.004
#> GSM907853 2 0.1474 0.7718 0.052 0.948 0.000 0.000
#> GSM907807 1 0.0921 0.8681 0.972 0.000 0.000 0.028
#> GSM907813 4 0.4989 0.0362 0.472 0.000 0.000 0.528
#> GSM907814 4 0.4967 0.0961 0.452 0.000 0.000 0.548
#> GSM907816 1 0.1109 0.8680 0.968 0.004 0.000 0.028
#> GSM907818 1 0.2961 0.8376 0.904 0.040 0.044 0.012
#> GSM907819 1 0.2741 0.8091 0.892 0.000 0.096 0.012
#> GSM907820 1 0.4978 0.5324 0.664 0.324 0.000 0.012
#> GSM907822 1 0.1576 0.8568 0.948 0.004 0.000 0.048
#> GSM907823 1 0.0895 0.8707 0.976 0.004 0.000 0.020
#> GSM907808 1 0.0336 0.8725 0.992 0.000 0.000 0.008
#> GSM907809 1 0.0336 0.8727 0.992 0.000 0.000 0.008
#> GSM907810 1 0.0707 0.8704 0.980 0.000 0.000 0.020
#> GSM907811 1 0.1305 0.8641 0.960 0.036 0.000 0.004
#> GSM907812 1 0.0376 0.8731 0.992 0.000 0.004 0.004
#> GSM907815 3 0.0376 0.6699 0.004 0.000 0.992 0.004
#> GSM907817 1 0.3529 0.7641 0.836 0.152 0.000 0.012
#> GSM907821 1 0.6692 0.3601 0.520 0.060 0.408 0.012
#> GSM907824 1 0.7014 0.5465 0.620 0.184 0.184 0.012
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.2233 0.6575 0.000 0.000 0.904 0.016 0.080
#> GSM907859 4 0.1278 0.7315 0.000 0.020 0.016 0.960 0.004
#> GSM907860 3 0.3639 0.7270 0.000 0.184 0.792 0.024 0.000
#> GSM907854 3 0.1671 0.6601 0.000 0.000 0.924 0.000 0.076
#> GSM907855 3 0.2562 0.7239 0.000 0.060 0.900 0.032 0.008
#> GSM907856 3 0.2541 0.7007 0.000 0.020 0.900 0.068 0.012
#> GSM907857 3 0.2848 0.5787 0.000 0.000 0.840 0.004 0.156
#> GSM907825 2 0.4717 0.6543 0.008 0.692 0.024 0.004 0.272
#> GSM907828 2 0.2037 0.7715 0.000 0.920 0.064 0.004 0.012
#> GSM907832 2 0.3639 0.7442 0.000 0.808 0.008 0.020 0.164
#> GSM907833 2 0.3804 0.7409 0.000 0.796 0.000 0.044 0.160
#> GSM907834 2 0.4025 0.6524 0.000 0.700 0.008 0.000 0.292
#> GSM907826 2 0.2358 0.7449 0.000 0.888 0.104 0.008 0.000
#> GSM907827 3 0.4535 0.6623 0.000 0.288 0.684 0.004 0.024
#> GSM907829 5 0.3769 0.5891 0.000 0.032 0.180 0.000 0.788
#> GSM907830 2 0.7266 0.3582 0.012 0.536 0.232 0.176 0.044
#> GSM907831 3 0.5009 0.2498 0.000 0.480 0.496 0.012 0.012
#> GSM907792 1 0.0510 0.8749 0.984 0.000 0.000 0.000 0.016
#> GSM907795 1 0.0798 0.8743 0.976 0.000 0.000 0.008 0.016
#> GSM907801 1 0.1195 0.8686 0.960 0.000 0.000 0.012 0.028
#> GSM907802 1 0.6661 0.1524 0.484 0.184 0.004 0.004 0.324
#> GSM907804 1 0.2879 0.8122 0.868 0.000 0.000 0.100 0.032
#> GSM907805 1 0.5115 0.6599 0.720 0.012 0.000 0.160 0.108
#> GSM907806 1 0.1502 0.8613 0.940 0.000 0.000 0.004 0.056
#> GSM907793 1 0.0324 0.8760 0.992 0.000 0.000 0.004 0.004
#> GSM907794 1 0.0324 0.8772 0.992 0.000 0.000 0.004 0.004
#> GSM907796 1 0.4737 0.6247 0.708 0.000 0.068 0.000 0.224
#> GSM907797 5 0.5554 0.4877 0.100 0.000 0.264 0.004 0.632
#> GSM907798 1 0.4272 0.7000 0.752 0.000 0.052 0.000 0.196
#> GSM907799 1 0.0290 0.8756 0.992 0.000 0.000 0.000 0.008
#> GSM907800 1 0.2616 0.8418 0.900 0.008 0.008 0.016 0.068
#> GSM907803 1 0.0324 0.8764 0.992 0.000 0.004 0.000 0.004
#> GSM907864 4 0.3563 0.6480 0.000 0.208 0.012 0.780 0.000
#> GSM907865 4 0.1124 0.7173 0.000 0.004 0.036 0.960 0.000
#> GSM907868 3 0.1717 0.7194 0.000 0.052 0.936 0.004 0.008
#> GSM907869 4 0.5831 0.1011 0.000 0.000 0.408 0.496 0.096
#> GSM907870 2 0.3140 0.7741 0.008 0.880 0.064 0.020 0.028
#> GSM907861 3 0.3596 0.7126 0.000 0.200 0.784 0.000 0.016
#> GSM907862 3 0.3906 0.7021 0.000 0.240 0.744 0.016 0.000
#> GSM907863 3 0.3916 0.6917 0.000 0.256 0.732 0.012 0.000
#> GSM907866 3 0.3159 0.6041 0.000 0.000 0.856 0.056 0.088
#> GSM907867 3 0.3353 0.7259 0.000 0.196 0.796 0.008 0.000
#> GSM907839 4 0.3500 0.6827 0.000 0.172 0.016 0.808 0.004
#> GSM907840 4 0.2300 0.7340 0.000 0.072 0.024 0.904 0.000
#> GSM907842 2 0.4473 0.3113 0.000 0.580 0.008 0.412 0.000
#> GSM907843 2 0.1059 0.7883 0.000 0.968 0.020 0.008 0.004
#> GSM907845 5 0.2959 0.5047 0.000 0.100 0.036 0.000 0.864
#> GSM907846 2 0.7786 0.1157 0.032 0.440 0.060 0.356 0.112
#> GSM907848 2 0.2753 0.7635 0.000 0.856 0.000 0.008 0.136
#> GSM907851 2 0.3858 0.7525 0.060 0.836 0.004 0.020 0.080
#> GSM907835 2 0.1357 0.7894 0.000 0.948 0.004 0.000 0.048
#> GSM907836 2 0.1341 0.7706 0.000 0.944 0.056 0.000 0.000
#> GSM907837 2 0.2971 0.6921 0.000 0.836 0.156 0.008 0.000
#> GSM907838 2 0.3388 0.6322 0.000 0.792 0.200 0.008 0.000
#> GSM907841 3 0.6555 0.0841 0.000 0.012 0.540 0.240 0.208
#> GSM907844 2 0.2329 0.7248 0.000 0.876 0.124 0.000 0.000
#> GSM907847 2 0.2513 0.7722 0.000 0.876 0.000 0.008 0.116
#> GSM907849 2 0.0771 0.7856 0.004 0.976 0.020 0.000 0.000
#> GSM907850 2 0.1991 0.7849 0.000 0.916 0.004 0.004 0.076
#> GSM907852 2 0.1095 0.7905 0.000 0.968 0.012 0.008 0.012
#> GSM907853 2 0.2970 0.7497 0.004 0.828 0.000 0.000 0.168
#> GSM907807 1 0.0324 0.8763 0.992 0.000 0.000 0.004 0.004
#> GSM907813 4 0.3706 0.5054 0.236 0.004 0.000 0.756 0.004
#> GSM907814 4 0.2127 0.6785 0.108 0.000 0.000 0.892 0.000
#> GSM907816 1 0.0566 0.8768 0.984 0.000 0.000 0.004 0.012
#> GSM907818 1 0.5012 0.4465 0.600 0.032 0.000 0.004 0.364
#> GSM907819 1 0.4347 0.7060 0.756 0.000 0.016 0.028 0.200
#> GSM907820 2 0.6433 0.2709 0.328 0.532 0.004 0.012 0.124
#> GSM907822 1 0.0000 0.8757 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.1579 0.8627 0.944 0.000 0.000 0.024 0.032
#> GSM907808 1 0.0290 0.8757 0.992 0.000 0.000 0.000 0.008
#> GSM907809 1 0.0771 0.8744 0.976 0.000 0.000 0.004 0.020
#> GSM907810 1 0.0162 0.8757 0.996 0.000 0.000 0.000 0.004
#> GSM907811 1 0.1370 0.8698 0.960 0.012 0.004 0.012 0.012
#> GSM907812 1 0.1502 0.8595 0.940 0.000 0.000 0.004 0.056
#> GSM907815 5 0.4360 0.5190 0.000 0.000 0.284 0.024 0.692
#> GSM907817 1 0.3410 0.8139 0.860 0.040 0.004 0.016 0.080
#> GSM907821 5 0.6759 0.0174 0.412 0.052 0.072 0.004 0.460
#> GSM907824 1 0.5340 0.6526 0.720 0.096 0.008 0.016 0.160
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.2877 0.7348 0.000 0.000 0.820 0.012 0.000 0.168
#> GSM907859 4 0.0922 0.8002 0.000 0.024 0.004 0.968 0.004 0.000
#> GSM907860 3 0.2292 0.8047 0.000 0.104 0.884 0.004 0.004 0.004
#> GSM907854 3 0.1918 0.7889 0.000 0.008 0.904 0.000 0.000 0.088
#> GSM907855 3 0.1540 0.8135 0.000 0.012 0.948 0.012 0.012 0.016
#> GSM907856 3 0.1862 0.8084 0.000 0.008 0.932 0.032 0.012 0.016
#> GSM907857 3 0.3104 0.6900 0.000 0.000 0.800 0.000 0.016 0.184
#> GSM907825 2 0.4786 0.6568 0.000 0.724 0.036 0.000 0.144 0.096
#> GSM907828 2 0.2344 0.7738 0.000 0.892 0.076 0.000 0.028 0.004
#> GSM907832 2 0.3473 0.7089 0.000 0.828 0.004 0.016 0.044 0.108
#> GSM907833 2 0.3659 0.6882 0.000 0.808 0.000 0.032 0.128 0.032
#> GSM907834 5 0.5807 0.2455 0.000 0.308 0.000 0.000 0.484 0.208
#> GSM907826 2 0.2760 0.7516 0.000 0.856 0.116 0.000 0.024 0.004
#> GSM907827 3 0.4896 0.6617 0.000 0.192 0.696 0.000 0.084 0.028
#> GSM907829 6 0.5200 0.3426 0.000 0.104 0.088 0.000 0.104 0.704
#> GSM907830 5 0.7006 0.1144 0.000 0.356 0.044 0.176 0.404 0.020
#> GSM907831 2 0.5169 0.2436 0.000 0.536 0.380 0.000 0.080 0.004
#> GSM907792 1 0.0000 0.7803 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0748 0.7789 0.976 0.000 0.000 0.004 0.016 0.004
#> GSM907801 1 0.2230 0.7448 0.892 0.000 0.000 0.000 0.084 0.024
#> GSM907802 1 0.7339 -0.1831 0.364 0.148 0.000 0.000 0.320 0.168
#> GSM907804 1 0.4618 0.6118 0.708 0.008 0.000 0.024 0.224 0.036
#> GSM907805 1 0.5344 0.5114 0.660 0.000 0.000 0.176 0.132 0.032
#> GSM907806 1 0.3830 0.2901 0.620 0.000 0.000 0.000 0.376 0.004
#> GSM907793 1 0.1096 0.7778 0.964 0.004 0.000 0.004 0.020 0.008
#> GSM907794 1 0.0551 0.7814 0.984 0.004 0.000 0.000 0.008 0.004
#> GSM907796 1 0.5748 0.3845 0.604 0.000 0.032 0.000 0.152 0.212
#> GSM907797 5 0.5966 0.0826 0.056 0.000 0.080 0.000 0.524 0.340
#> GSM907798 1 0.4501 0.6251 0.748 0.000 0.028 0.000 0.124 0.100
#> GSM907799 1 0.0777 0.7779 0.972 0.000 0.000 0.000 0.024 0.004
#> GSM907800 5 0.4046 0.3286 0.368 0.008 0.000 0.000 0.620 0.004
#> GSM907803 1 0.1285 0.7637 0.944 0.000 0.000 0.000 0.052 0.004
#> GSM907864 4 0.2400 0.7490 0.000 0.116 0.008 0.872 0.004 0.000
#> GSM907865 4 0.0508 0.7903 0.000 0.000 0.004 0.984 0.000 0.012
#> GSM907868 3 0.1480 0.8118 0.000 0.020 0.940 0.000 0.000 0.040
#> GSM907869 4 0.5872 0.0349 0.000 0.000 0.220 0.508 0.004 0.268
#> GSM907870 2 0.5248 0.5793 0.000 0.684 0.060 0.008 0.196 0.052
#> GSM907861 3 0.3220 0.7930 0.000 0.108 0.832 0.000 0.004 0.056
#> GSM907862 3 0.2809 0.7584 0.000 0.168 0.824 0.000 0.004 0.004
#> GSM907863 3 0.2920 0.7574 0.000 0.168 0.820 0.000 0.008 0.004
#> GSM907866 3 0.2911 0.7174 0.000 0.000 0.832 0.024 0.000 0.144
#> GSM907867 3 0.2101 0.8060 0.000 0.100 0.892 0.000 0.004 0.004
#> GSM907839 4 0.3245 0.6548 0.000 0.184 0.016 0.796 0.004 0.000
#> GSM907840 4 0.1116 0.8017 0.000 0.028 0.008 0.960 0.000 0.004
#> GSM907842 2 0.4063 0.2832 0.000 0.572 0.004 0.420 0.004 0.000
#> GSM907843 2 0.1026 0.7773 0.000 0.968 0.008 0.012 0.008 0.004
#> GSM907845 5 0.5547 0.1423 0.000 0.148 0.000 0.000 0.508 0.344
#> GSM907846 6 0.7902 0.1932 0.008 0.272 0.012 0.132 0.224 0.352
#> GSM907848 2 0.2946 0.6876 0.000 0.824 0.000 0.012 0.160 0.004
#> GSM907851 2 0.5126 0.5884 0.024 0.704 0.012 0.008 0.188 0.064
#> GSM907835 2 0.1151 0.7791 0.000 0.956 0.032 0.000 0.012 0.000
#> GSM907836 2 0.1787 0.7781 0.000 0.920 0.068 0.004 0.008 0.000
#> GSM907837 2 0.3752 0.7011 0.000 0.776 0.168 0.000 0.052 0.004
#> GSM907838 2 0.4981 0.5887 0.004 0.668 0.204 0.000 0.120 0.004
#> GSM907841 6 0.6094 0.1347 0.000 0.000 0.312 0.300 0.000 0.388
#> GSM907844 2 0.3172 0.7329 0.000 0.824 0.128 0.000 0.048 0.000
#> GSM907847 2 0.1675 0.7627 0.000 0.936 0.000 0.008 0.032 0.024
#> GSM907849 2 0.1152 0.7790 0.000 0.952 0.044 0.000 0.000 0.004
#> GSM907850 2 0.1476 0.7775 0.000 0.948 0.008 0.004 0.028 0.012
#> GSM907852 2 0.1391 0.7802 0.000 0.944 0.040 0.000 0.016 0.000
#> GSM907853 2 0.3448 0.5439 0.000 0.716 0.000 0.004 0.280 0.000
#> GSM907807 1 0.0405 0.7801 0.988 0.000 0.000 0.004 0.008 0.000
#> GSM907813 4 0.2518 0.7273 0.088 0.012 0.000 0.884 0.012 0.004
#> GSM907814 4 0.1196 0.7832 0.040 0.000 0.000 0.952 0.000 0.008
#> GSM907816 1 0.1226 0.7707 0.952 0.000 0.000 0.004 0.040 0.004
#> GSM907818 5 0.5147 0.3068 0.356 0.000 0.000 0.000 0.548 0.096
#> GSM907819 1 0.6488 0.2194 0.476 0.008 0.016 0.004 0.200 0.296
#> GSM907820 5 0.6049 0.1841 0.144 0.384 0.000 0.000 0.452 0.020
#> GSM907822 1 0.0436 0.7814 0.988 0.000 0.000 0.004 0.004 0.004
#> GSM907823 1 0.4492 0.5979 0.720 0.012 0.000 0.004 0.204 0.060
#> GSM907808 1 0.0260 0.7805 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907809 1 0.1982 0.7561 0.912 0.000 0.000 0.004 0.068 0.016
#> GSM907810 1 0.0000 0.7803 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2632 0.6717 0.832 0.000 0.000 0.000 0.164 0.004
#> GSM907812 1 0.4184 0.4274 0.672 0.000 0.028 0.000 0.296 0.004
#> GSM907815 6 0.4390 0.3993 0.000 0.000 0.172 0.052 0.032 0.744
#> GSM907817 5 0.4930 0.2660 0.404 0.048 0.000 0.000 0.540 0.008
#> GSM907821 6 0.7398 -0.0206 0.308 0.064 0.032 0.000 0.184 0.412
#> GSM907824 5 0.4461 0.4237 0.304 0.028 0.008 0.000 0.656 0.004
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
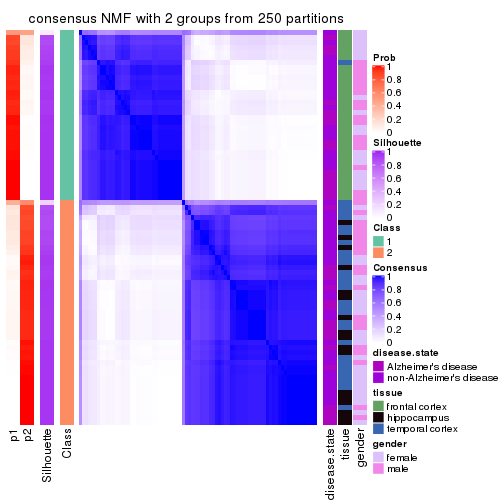
consensus_heatmap(res, k = 3)
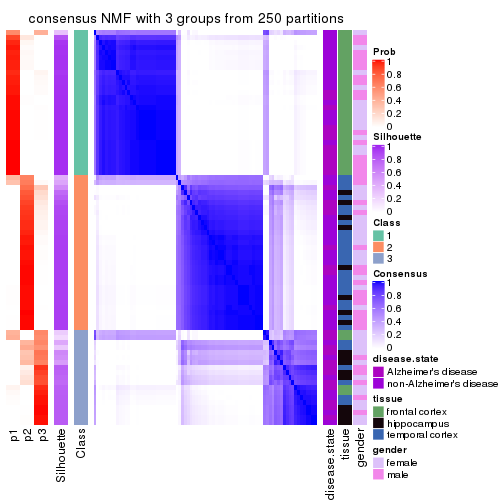
consensus_heatmap(res, k = 4)
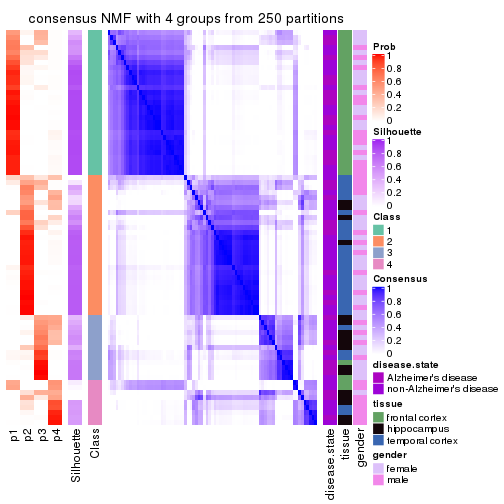
consensus_heatmap(res, k = 5)
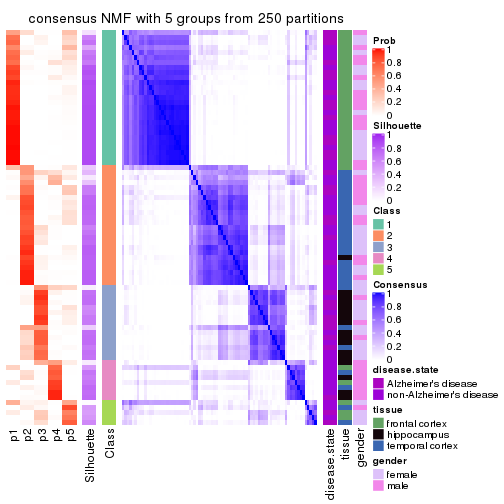
consensus_heatmap(res, k = 6)
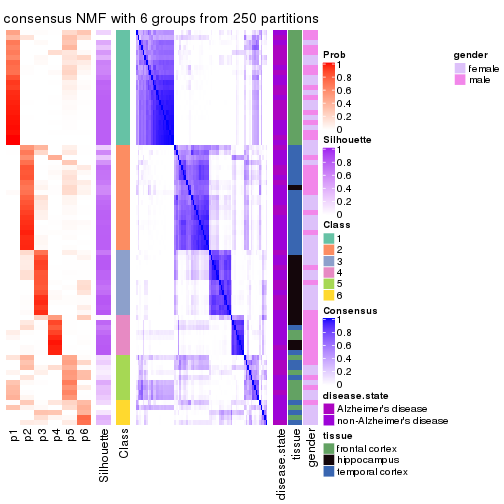
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
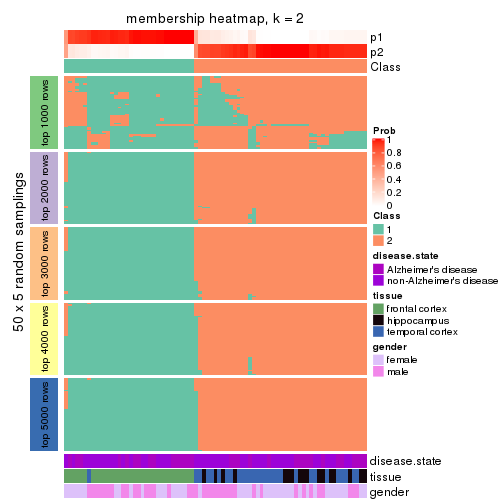
membership_heatmap(res, k = 3)
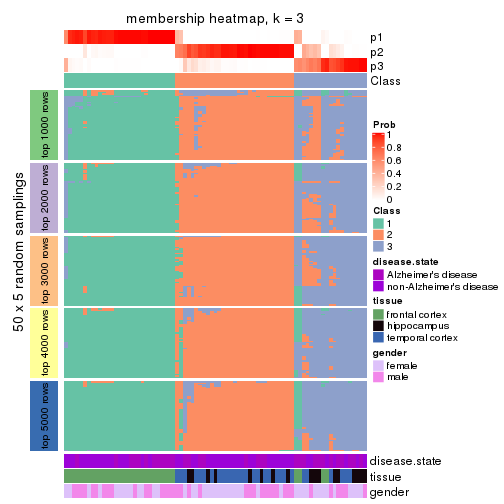
membership_heatmap(res, k = 4)
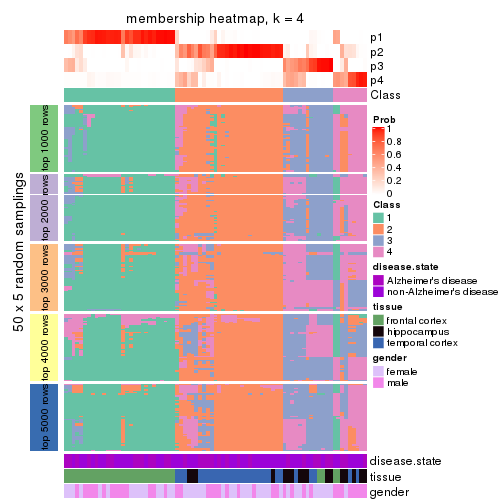
membership_heatmap(res, k = 5)
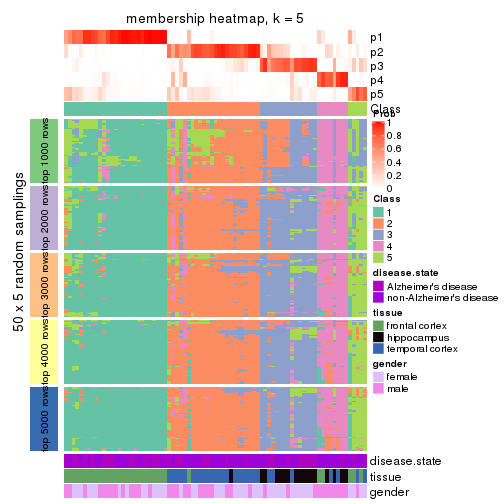
membership_heatmap(res, k = 6)
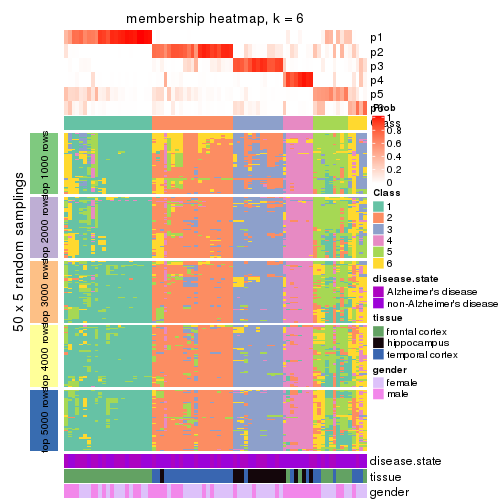
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
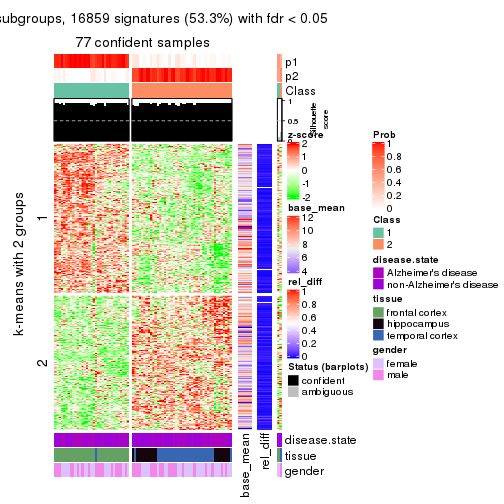
get_signatures(res, k = 3)
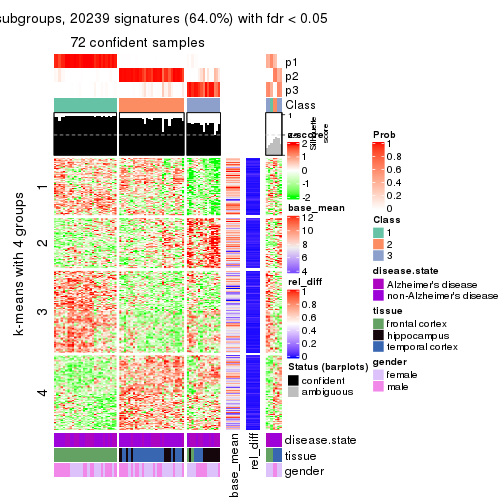
get_signatures(res, k = 4)
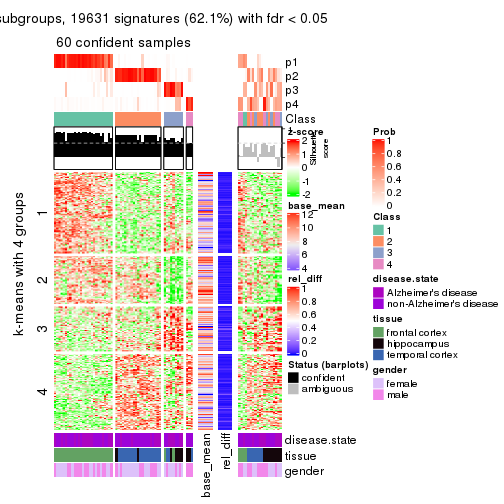
get_signatures(res, k = 5)
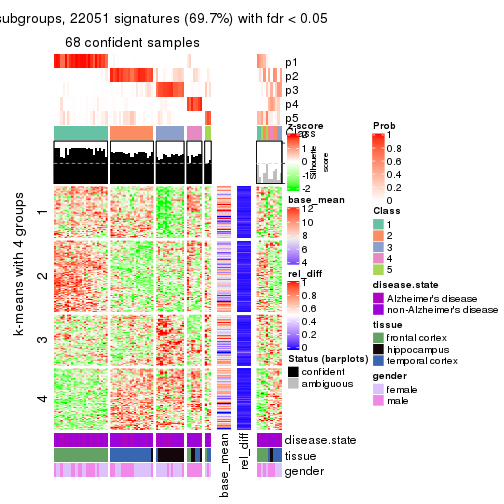
get_signatures(res, k = 6)
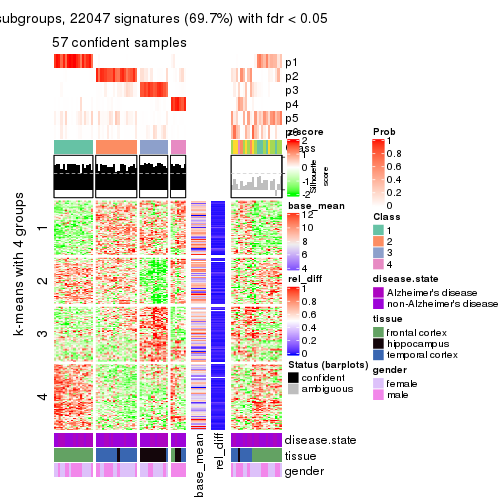
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
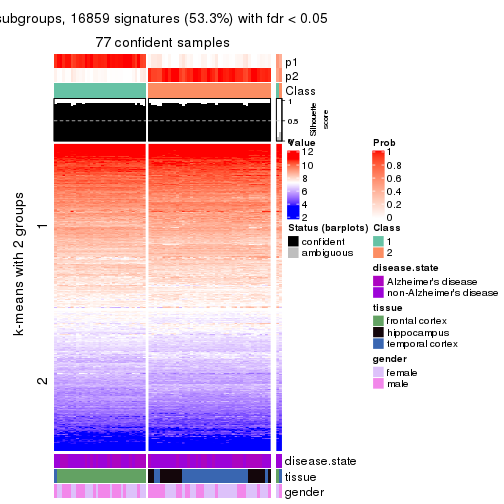
get_signatures(res, k = 3, scale_rows = FALSE)
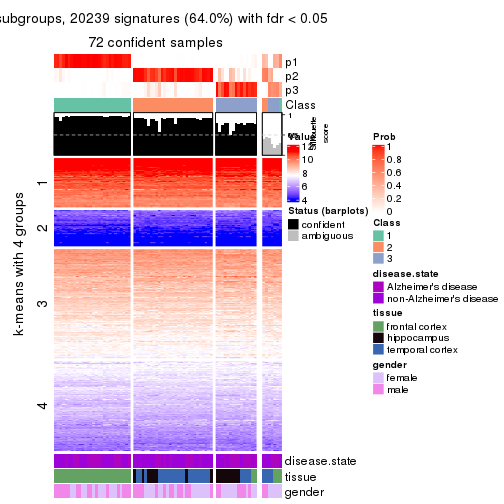
get_signatures(res, k = 4, scale_rows = FALSE)
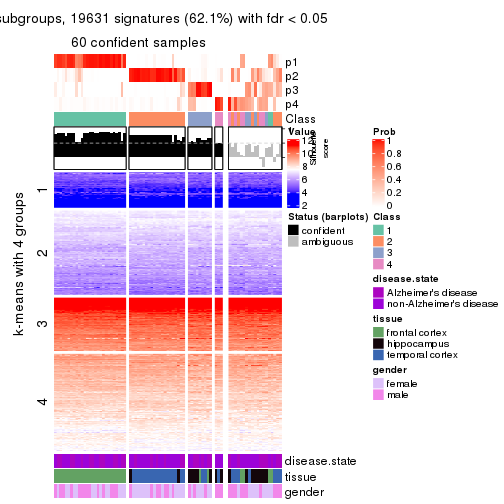
get_signatures(res, k = 5, scale_rows = FALSE)
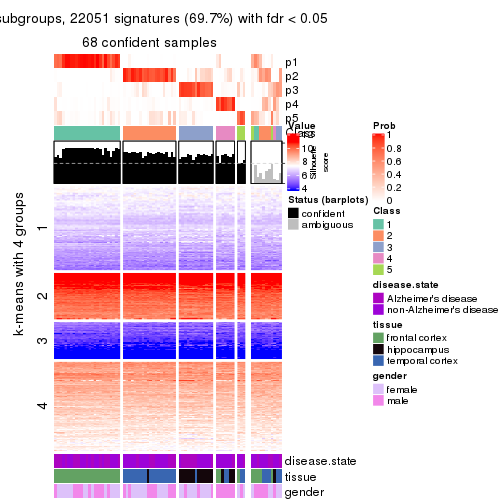
get_signatures(res, k = 6, scale_rows = FALSE)
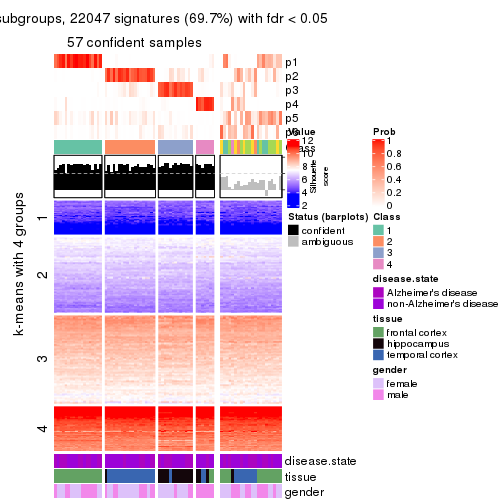
Compare the overlap of signatures from different k:
compare_signatures(res)
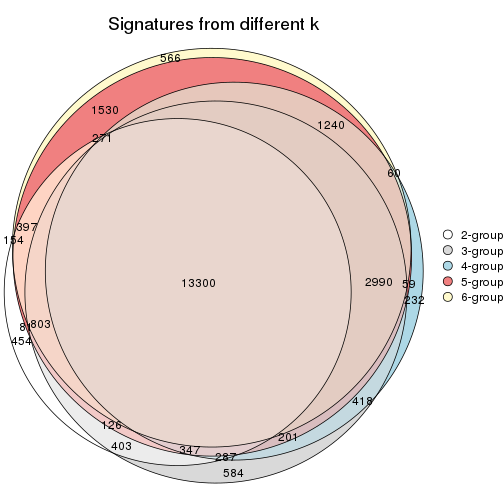
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
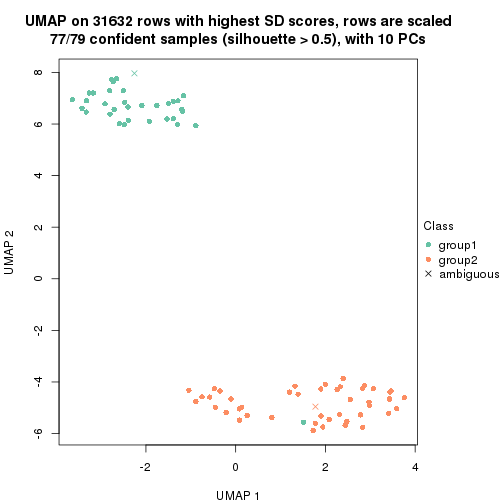
dimension_reduction(res, k = 3, method = "UMAP")
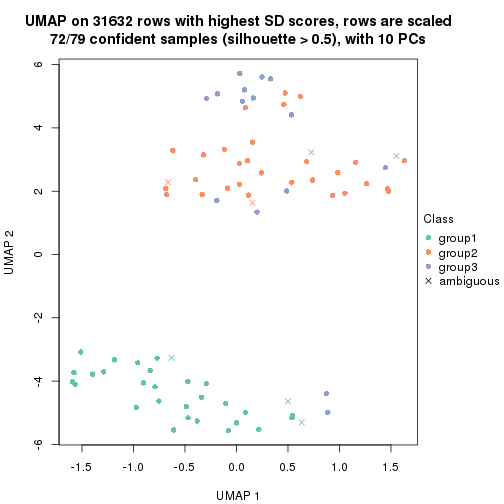
dimension_reduction(res, k = 4, method = "UMAP")
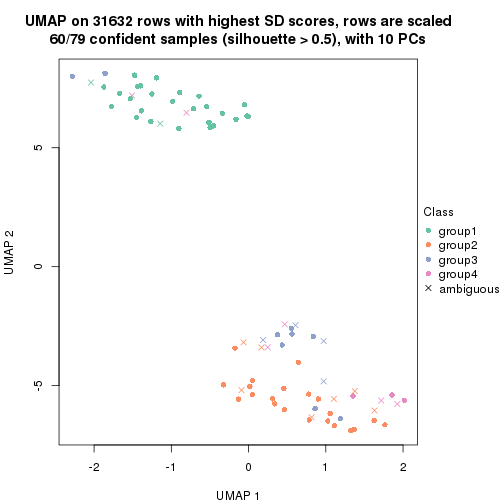
dimension_reduction(res, k = 5, method = "UMAP")
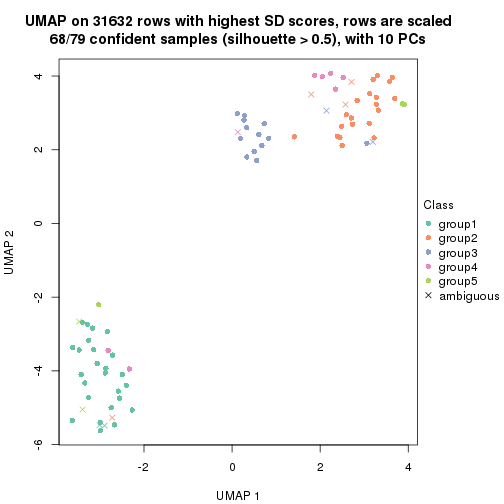
dimension_reduction(res, k = 6, method = "UMAP")
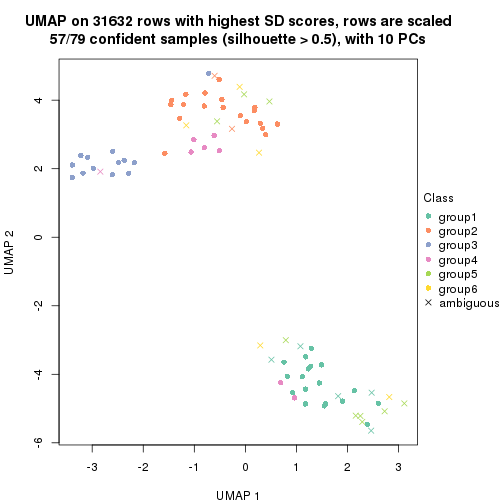
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
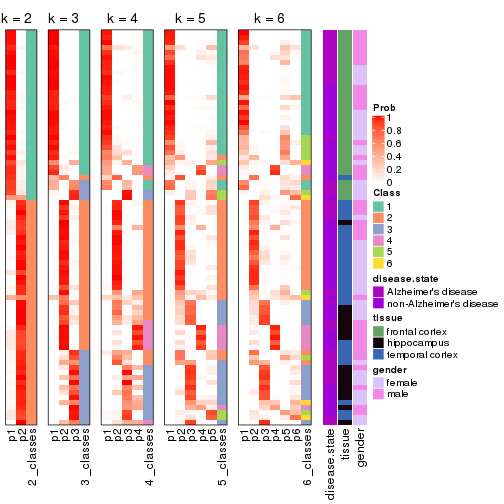
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> SD:NMF 77 0.714 1.36e-16 0.6209 2
#> SD:NMF 72 0.108 2.07e-15 0.4898 3
#> SD:NMF 60 0.187 4.95e-14 0.1203 4
#> SD:NMF 68 0.261 5.31e-19 0.0242 5
#> SD:NMF 57 0.100 7.15e-17 0.0111 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "hclust"]
# you can also extract it by
# res = res_list["CV:hclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'hclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
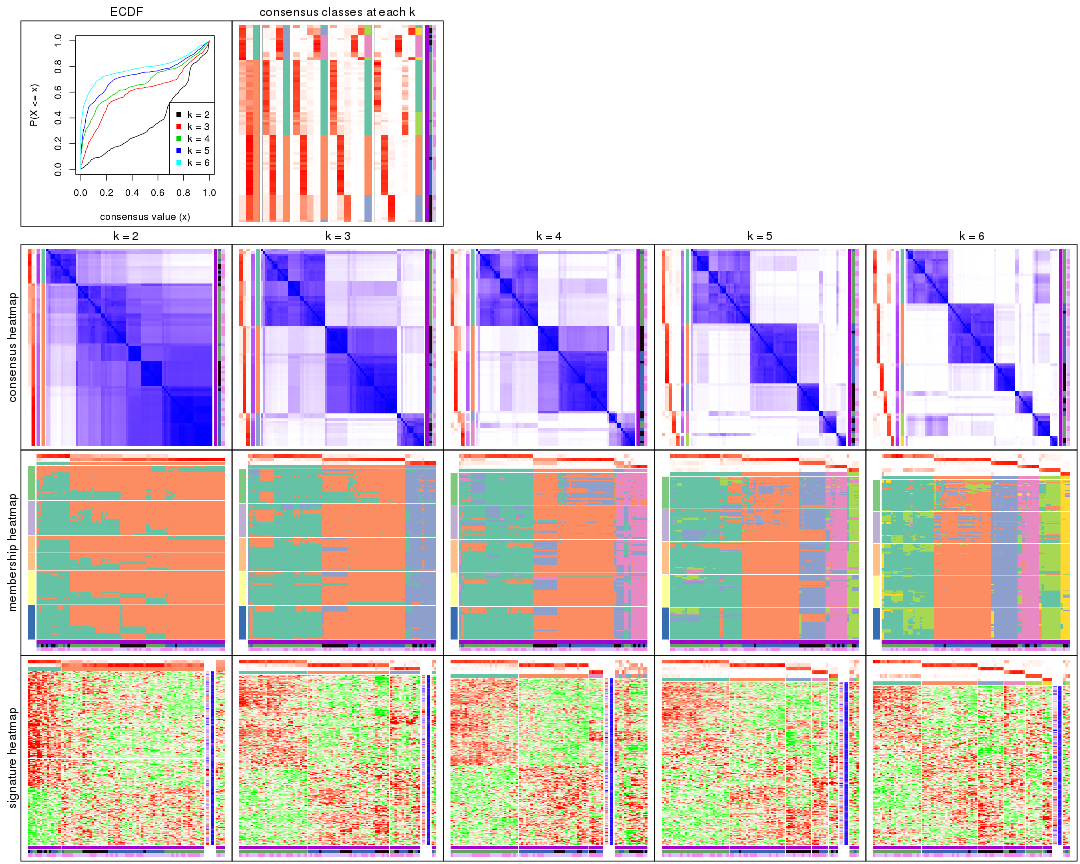
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
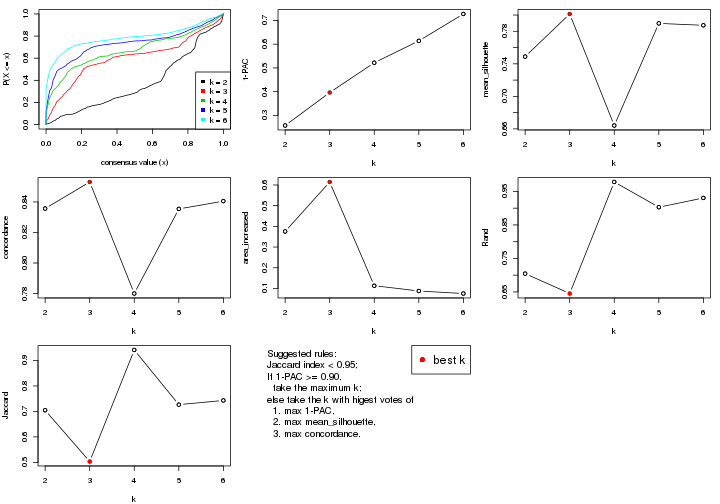
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.257 0.749 0.836 0.3753 0.705 0.705
#> 3 3 0.396 0.801 0.853 0.6145 0.645 0.503
#> 4 4 0.522 0.664 0.780 0.1131 0.978 0.941
#> 5 5 0.614 0.790 0.835 0.0877 0.903 0.727
#> 6 6 0.727 0.787 0.841 0.0755 0.931 0.743
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.6247 0.772 0.156 0.844
#> GSM907859 1 0.4815 0.893 0.896 0.104
#> GSM907860 2 0.6048 0.774 0.148 0.852
#> GSM907854 2 0.6148 0.774 0.152 0.848
#> GSM907855 2 0.6148 0.774 0.152 0.848
#> GSM907856 2 0.6247 0.773 0.156 0.844
#> GSM907857 2 0.9087 0.618 0.324 0.676
#> GSM907825 2 0.0376 0.782 0.004 0.996
#> GSM907828 2 0.0376 0.785 0.004 0.996
#> GSM907832 2 0.0000 0.783 0.000 1.000
#> GSM907833 2 0.0672 0.786 0.008 0.992
#> GSM907834 2 0.0376 0.782 0.004 0.996
#> GSM907826 2 0.0672 0.786 0.008 0.992
#> GSM907827 2 0.0376 0.785 0.004 0.996
#> GSM907829 2 0.3274 0.794 0.060 0.940
#> GSM907830 1 0.8144 0.691 0.748 0.252
#> GSM907831 2 0.0376 0.782 0.004 0.996
#> GSM907792 2 0.9393 0.659 0.356 0.644
#> GSM907795 2 0.9998 0.446 0.492 0.508
#> GSM907801 2 0.9795 0.577 0.416 0.584
#> GSM907802 2 0.6247 0.779 0.156 0.844
#> GSM907804 2 0.8327 0.740 0.264 0.736
#> GSM907805 2 0.9580 0.641 0.380 0.620
#> GSM907806 2 0.8955 0.700 0.312 0.688
#> GSM907793 2 0.9977 0.490 0.472 0.528
#> GSM907794 2 0.8713 0.716 0.292 0.708
#> GSM907796 2 0.9881 0.562 0.436 0.564
#> GSM907797 1 0.7745 0.625 0.772 0.228
#> GSM907798 2 0.9815 0.588 0.420 0.580
#> GSM907799 2 0.9087 0.690 0.324 0.676
#> GSM907800 2 0.6343 0.779 0.160 0.840
#> GSM907803 2 0.9087 0.688 0.324 0.676
#> GSM907864 1 0.3114 0.922 0.944 0.056
#> GSM907865 1 0.0938 0.907 0.988 0.012
#> GSM907868 2 0.6148 0.774 0.152 0.848
#> GSM907869 1 0.2778 0.919 0.952 0.048
#> GSM907870 2 0.1843 0.790 0.028 0.972
#> GSM907861 2 0.6148 0.774 0.152 0.848
#> GSM907862 2 0.6048 0.774 0.148 0.852
#> GSM907863 2 0.6048 0.774 0.148 0.852
#> GSM907866 1 0.3879 0.914 0.924 0.076
#> GSM907867 2 0.5946 0.775 0.144 0.856
#> GSM907839 1 0.3114 0.922 0.944 0.056
#> GSM907840 1 0.2043 0.914 0.968 0.032
#> GSM907842 1 0.3733 0.918 0.928 0.072
#> GSM907843 2 0.0376 0.785 0.004 0.996
#> GSM907845 2 0.3879 0.792 0.076 0.924
#> GSM907846 2 0.7528 0.767 0.216 0.784
#> GSM907848 2 0.0672 0.783 0.008 0.992
#> GSM907851 2 0.2778 0.791 0.048 0.952
#> GSM907835 2 0.0376 0.782 0.004 0.996
#> GSM907836 2 0.0376 0.782 0.004 0.996
#> GSM907837 2 0.0376 0.782 0.004 0.996
#> GSM907838 2 0.0376 0.782 0.004 0.996
#> GSM907841 1 0.3879 0.914 0.924 0.076
#> GSM907844 2 0.0000 0.783 0.000 1.000
#> GSM907847 2 0.0376 0.785 0.004 0.996
#> GSM907849 2 0.0938 0.787 0.012 0.988
#> GSM907850 2 0.0000 0.783 0.000 1.000
#> GSM907852 2 0.0376 0.782 0.004 0.996
#> GSM907853 2 0.0672 0.786 0.008 0.992
#> GSM907807 2 0.9963 0.509 0.464 0.536
#> GSM907813 1 0.2043 0.914 0.968 0.032
#> GSM907814 1 0.2043 0.914 0.968 0.032
#> GSM907816 2 0.9170 0.682 0.332 0.668
#> GSM907818 2 0.9209 0.690 0.336 0.664
#> GSM907819 2 0.8555 0.728 0.280 0.720
#> GSM907820 2 0.6247 0.779 0.156 0.844
#> GSM907822 2 0.9248 0.673 0.340 0.660
#> GSM907823 2 0.9323 0.665 0.348 0.652
#> GSM907808 2 0.9988 0.474 0.480 0.520
#> GSM907809 2 0.9988 0.474 0.480 0.520
#> GSM907810 2 0.9710 0.617 0.400 0.600
#> GSM907811 2 0.9087 0.688 0.324 0.676
#> GSM907812 2 0.9881 0.562 0.436 0.564
#> GSM907815 1 0.0376 0.903 0.996 0.004
#> GSM907817 2 0.6343 0.779 0.160 0.840
#> GSM907821 2 0.6247 0.779 0.156 0.844
#> GSM907824 2 0.6247 0.779 0.156 0.844
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 2 0.6168 0.8094 0.096 0.780 0.124
#> GSM907859 3 0.4095 0.8441 0.064 0.056 0.880
#> GSM907860 2 0.6037 0.8158 0.100 0.788 0.112
#> GSM907854 2 0.6111 0.8140 0.104 0.784 0.112
#> GSM907855 2 0.6111 0.8140 0.104 0.784 0.112
#> GSM907856 2 0.6181 0.8108 0.104 0.780 0.116
#> GSM907857 2 0.8489 0.5598 0.136 0.596 0.268
#> GSM907825 2 0.1411 0.8850 0.036 0.964 0.000
#> GSM907828 2 0.2301 0.8892 0.060 0.936 0.004
#> GSM907832 2 0.3116 0.8444 0.108 0.892 0.000
#> GSM907833 2 0.2845 0.8875 0.068 0.920 0.012
#> GSM907834 2 0.1411 0.8815 0.036 0.964 0.000
#> GSM907826 2 0.1989 0.8902 0.048 0.948 0.004
#> GSM907827 2 0.2096 0.8896 0.052 0.944 0.004
#> GSM907829 2 0.4195 0.8473 0.136 0.852 0.012
#> GSM907830 3 0.5503 0.6828 0.020 0.208 0.772
#> GSM907831 2 0.1031 0.8838 0.024 0.976 0.000
#> GSM907792 1 0.4413 0.8398 0.852 0.124 0.024
#> GSM907795 1 0.1529 0.7589 0.960 0.000 0.040
#> GSM907801 1 0.3530 0.8151 0.900 0.068 0.032
#> GSM907802 1 0.5835 0.7168 0.660 0.340 0.000
#> GSM907804 1 0.6446 0.8025 0.736 0.212 0.052
#> GSM907805 1 0.5285 0.8154 0.824 0.112 0.064
#> GSM907806 1 0.3983 0.8405 0.852 0.144 0.004
#> GSM907793 1 0.2152 0.7785 0.948 0.016 0.036
#> GSM907794 1 0.4409 0.8330 0.824 0.172 0.004
#> GSM907796 1 0.2689 0.7897 0.932 0.032 0.036
#> GSM907797 1 0.6688 -0.0823 0.580 0.012 0.408
#> GSM907798 1 0.1647 0.8037 0.960 0.036 0.004
#> GSM907799 1 0.4261 0.8417 0.848 0.140 0.012
#> GSM907800 1 0.5835 0.7167 0.660 0.340 0.000
#> GSM907803 1 0.4326 0.8416 0.844 0.144 0.012
#> GSM907864 3 0.1781 0.8748 0.020 0.020 0.960
#> GSM907865 3 0.0892 0.8669 0.020 0.000 0.980
#> GSM907868 2 0.6184 0.8122 0.108 0.780 0.112
#> GSM907869 3 0.3356 0.8668 0.056 0.036 0.908
#> GSM907870 2 0.2772 0.8832 0.080 0.916 0.004
#> GSM907861 2 0.6111 0.8140 0.104 0.784 0.112
#> GSM907862 2 0.6037 0.8158 0.100 0.788 0.112
#> GSM907863 2 0.6037 0.8158 0.100 0.788 0.112
#> GSM907866 3 0.3692 0.8659 0.048 0.056 0.896
#> GSM907867 2 0.5965 0.8185 0.100 0.792 0.108
#> GSM907839 3 0.1781 0.8748 0.020 0.020 0.960
#> GSM907840 3 0.0848 0.8700 0.008 0.008 0.984
#> GSM907842 3 0.2313 0.8721 0.024 0.032 0.944
#> GSM907843 2 0.2200 0.8896 0.056 0.940 0.004
#> GSM907845 2 0.4796 0.7434 0.220 0.780 0.000
#> GSM907846 1 0.8264 0.2730 0.488 0.436 0.076
#> GSM907848 2 0.1643 0.8818 0.044 0.956 0.000
#> GSM907851 2 0.3879 0.8278 0.152 0.848 0.000
#> GSM907835 2 0.1163 0.8857 0.028 0.972 0.000
#> GSM907836 2 0.1031 0.8838 0.024 0.976 0.000
#> GSM907837 2 0.1031 0.8838 0.024 0.976 0.000
#> GSM907838 2 0.1031 0.8838 0.024 0.976 0.000
#> GSM907841 3 0.3692 0.8659 0.048 0.056 0.896
#> GSM907844 2 0.1289 0.8856 0.032 0.968 0.000
#> GSM907847 2 0.2096 0.8896 0.052 0.944 0.004
#> GSM907849 2 0.2400 0.8888 0.064 0.932 0.004
#> GSM907850 2 0.1411 0.8868 0.036 0.964 0.000
#> GSM907852 2 0.1163 0.8837 0.028 0.972 0.000
#> GSM907853 2 0.2590 0.8873 0.072 0.924 0.004
#> GSM907807 1 0.2434 0.7871 0.940 0.024 0.036
#> GSM907813 3 0.6008 0.5515 0.372 0.000 0.628
#> GSM907814 3 0.6008 0.5515 0.372 0.000 0.628
#> GSM907816 1 0.4345 0.8415 0.848 0.136 0.016
#> GSM907818 1 0.3551 0.8390 0.868 0.132 0.000
#> GSM907819 1 0.6007 0.8157 0.764 0.192 0.044
#> GSM907820 1 0.5905 0.7070 0.648 0.352 0.000
#> GSM907822 1 0.3989 0.8407 0.864 0.124 0.012
#> GSM907823 1 0.4551 0.8421 0.840 0.140 0.020
#> GSM907808 1 0.2116 0.7733 0.948 0.012 0.040
#> GSM907809 1 0.2116 0.7733 0.948 0.012 0.040
#> GSM907810 1 0.3461 0.8257 0.900 0.076 0.024
#> GSM907811 1 0.4390 0.8411 0.840 0.148 0.012
#> GSM907812 1 0.2689 0.7897 0.932 0.032 0.036
#> GSM907815 3 0.3412 0.8339 0.124 0.000 0.876
#> GSM907817 1 0.5835 0.7167 0.660 0.340 0.000
#> GSM907821 1 0.5882 0.7112 0.652 0.348 0.000
#> GSM907824 1 0.5882 0.7112 0.652 0.348 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 2 0.7095 0.491 0.028 0.540 0.364 0.068
#> GSM907859 4 0.3720 0.599 0.032 0.032 0.064 0.872
#> GSM907860 2 0.6830 0.507 0.024 0.552 0.368 0.056
#> GSM907854 2 0.6830 0.504 0.024 0.552 0.368 0.056
#> GSM907855 2 0.6852 0.497 0.024 0.544 0.376 0.056
#> GSM907856 2 0.6906 0.494 0.024 0.544 0.372 0.060
#> GSM907857 3 0.7837 -0.274 0.080 0.364 0.496 0.060
#> GSM907825 2 0.1452 0.799 0.008 0.956 0.036 0.000
#> GSM907828 2 0.1545 0.803 0.008 0.952 0.040 0.000
#> GSM907832 2 0.3088 0.761 0.060 0.888 0.052 0.000
#> GSM907833 2 0.2089 0.802 0.020 0.932 0.048 0.000
#> GSM907834 2 0.1452 0.796 0.008 0.956 0.036 0.000
#> GSM907826 2 0.1022 0.804 0.000 0.968 0.032 0.000
#> GSM907827 2 0.1576 0.803 0.004 0.948 0.048 0.000
#> GSM907829 2 0.3754 0.752 0.092 0.856 0.048 0.004
#> GSM907830 4 0.4900 0.370 0.008 0.200 0.032 0.760
#> GSM907831 2 0.1022 0.801 0.000 0.968 0.032 0.000
#> GSM907792 1 0.3342 0.825 0.868 0.100 0.032 0.000
#> GSM907795 1 0.2466 0.740 0.900 0.000 0.096 0.004
#> GSM907801 1 0.3731 0.800 0.860 0.064 0.072 0.004
#> GSM907802 1 0.6273 0.715 0.636 0.264 0.100 0.000
#> GSM907804 1 0.6158 0.780 0.724 0.152 0.088 0.036
#> GSM907805 1 0.5167 0.792 0.800 0.084 0.064 0.052
#> GSM907806 1 0.3166 0.824 0.868 0.116 0.016 0.000
#> GSM907793 1 0.2665 0.757 0.900 0.008 0.088 0.004
#> GSM907794 1 0.3842 0.820 0.836 0.128 0.036 0.000
#> GSM907796 1 0.2586 0.778 0.912 0.008 0.068 0.012
#> GSM907797 1 0.7001 0.124 0.544 0.000 0.316 0.140
#> GSM907798 1 0.1635 0.790 0.948 0.008 0.044 0.000
#> GSM907799 1 0.2928 0.827 0.880 0.108 0.012 0.000
#> GSM907800 1 0.6194 0.722 0.644 0.260 0.096 0.000
#> GSM907803 1 0.2859 0.827 0.880 0.112 0.008 0.000
#> GSM907864 4 0.1593 0.651 0.004 0.016 0.024 0.956
#> GSM907865 4 0.0000 0.627 0.000 0.000 0.000 1.000
#> GSM907868 2 0.6929 0.498 0.028 0.544 0.372 0.056
#> GSM907869 3 0.4985 0.332 0.000 0.000 0.532 0.468
#> GSM907870 2 0.2081 0.793 0.000 0.916 0.084 0.000
#> GSM907861 2 0.6830 0.504 0.024 0.552 0.368 0.056
#> GSM907862 2 0.6805 0.517 0.024 0.560 0.360 0.056
#> GSM907863 2 0.6805 0.517 0.024 0.560 0.360 0.056
#> GSM907866 3 0.4948 0.377 0.000 0.000 0.560 0.440
#> GSM907867 2 0.6487 0.535 0.016 0.588 0.344 0.052
#> GSM907839 4 0.1593 0.651 0.004 0.016 0.024 0.956
#> GSM907840 4 0.0779 0.641 0.000 0.004 0.016 0.980
#> GSM907842 4 0.2023 0.643 0.004 0.028 0.028 0.940
#> GSM907843 2 0.1398 0.802 0.004 0.956 0.040 0.000
#> GSM907845 2 0.4375 0.665 0.180 0.788 0.032 0.000
#> GSM907846 1 0.8279 0.275 0.448 0.360 0.148 0.044
#> GSM907848 2 0.1677 0.796 0.012 0.948 0.040 0.000
#> GSM907851 2 0.3047 0.737 0.116 0.872 0.012 0.000
#> GSM907835 2 0.0469 0.800 0.000 0.988 0.012 0.000
#> GSM907836 2 0.0817 0.799 0.000 0.976 0.024 0.000
#> GSM907837 2 0.0921 0.794 0.000 0.972 0.028 0.000
#> GSM907838 2 0.0817 0.796 0.000 0.976 0.024 0.000
#> GSM907841 3 0.4948 0.377 0.000 0.000 0.560 0.440
#> GSM907844 2 0.1004 0.803 0.004 0.972 0.024 0.000
#> GSM907847 2 0.1305 0.803 0.004 0.960 0.036 0.000
#> GSM907849 2 0.1706 0.803 0.016 0.948 0.036 0.000
#> GSM907850 2 0.0657 0.801 0.004 0.984 0.012 0.000
#> GSM907852 2 0.1022 0.793 0.000 0.968 0.032 0.000
#> GSM907853 2 0.2032 0.801 0.028 0.936 0.036 0.000
#> GSM907807 1 0.2891 0.770 0.896 0.020 0.080 0.004
#> GSM907813 4 0.6457 0.379 0.296 0.000 0.100 0.604
#> GSM907814 4 0.6457 0.379 0.296 0.000 0.100 0.604
#> GSM907816 1 0.2988 0.827 0.876 0.112 0.012 0.000
#> GSM907818 1 0.3279 0.825 0.872 0.096 0.032 0.000
#> GSM907819 1 0.5720 0.793 0.752 0.144 0.072 0.032
#> GSM907820 1 0.6375 0.705 0.624 0.272 0.104 0.000
#> GSM907822 1 0.3245 0.825 0.872 0.100 0.028 0.000
#> GSM907823 1 0.3907 0.823 0.836 0.120 0.044 0.000
#> GSM907808 1 0.2861 0.755 0.892 0.012 0.092 0.004
#> GSM907809 1 0.2861 0.755 0.892 0.012 0.092 0.004
#> GSM907810 1 0.2578 0.811 0.912 0.052 0.036 0.000
#> GSM907811 1 0.2918 0.826 0.876 0.116 0.008 0.000
#> GSM907812 1 0.2586 0.778 0.912 0.008 0.068 0.012
#> GSM907815 4 0.6609 -0.285 0.080 0.000 0.448 0.472
#> GSM907817 1 0.6194 0.722 0.644 0.260 0.096 0.000
#> GSM907821 1 0.6378 0.711 0.628 0.264 0.108 0.000
#> GSM907824 1 0.6378 0.711 0.628 0.264 0.108 0.000
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.4080 0.9323 0.016 0.168 0.792 0.012 0.012
#> GSM907859 4 0.3554 0.7423 0.032 0.008 0.100 0.848 0.012
#> GSM907860 3 0.3355 0.9473 0.012 0.184 0.804 0.000 0.000
#> GSM907854 3 0.3391 0.9472 0.012 0.188 0.800 0.000 0.000
#> GSM907855 3 0.3280 0.9452 0.012 0.176 0.812 0.000 0.000
#> GSM907856 3 0.3559 0.9440 0.012 0.176 0.804 0.008 0.000
#> GSM907857 3 0.5964 0.6870 0.068 0.096 0.680 0.000 0.156
#> GSM907825 2 0.1492 0.9189 0.008 0.948 0.040 0.000 0.004
#> GSM907828 2 0.1864 0.9133 0.004 0.924 0.068 0.004 0.000
#> GSM907832 2 0.3073 0.8727 0.052 0.872 0.068 0.000 0.008
#> GSM907833 2 0.2770 0.9053 0.016 0.892 0.072 0.016 0.004
#> GSM907834 2 0.1329 0.9157 0.008 0.956 0.032 0.000 0.004
#> GSM907826 2 0.1197 0.9212 0.000 0.952 0.048 0.000 0.000
#> GSM907827 2 0.2233 0.8984 0.000 0.892 0.104 0.000 0.004
#> GSM907829 2 0.4146 0.8272 0.088 0.804 0.096 0.000 0.012
#> GSM907830 4 0.4490 0.5922 0.004 0.168 0.072 0.756 0.000
#> GSM907831 2 0.1430 0.9195 0.000 0.944 0.052 0.000 0.004
#> GSM907792 1 0.2978 0.7963 0.888 0.036 0.052 0.004 0.020
#> GSM907795 1 0.5112 0.6730 0.736 0.000 0.132 0.024 0.108
#> GSM907801 1 0.3873 0.7560 0.832 0.012 0.104 0.012 0.040
#> GSM907802 1 0.5669 0.6680 0.692 0.192 0.080 0.008 0.028
#> GSM907804 1 0.5010 0.7344 0.784 0.060 0.076 0.024 0.056
#> GSM907805 1 0.5054 0.7612 0.784 0.036 0.076 0.056 0.048
#> GSM907806 1 0.1282 0.7959 0.952 0.044 0.004 0.000 0.000
#> GSM907793 1 0.5126 0.6928 0.744 0.004 0.128 0.024 0.100
#> GSM907794 1 0.2131 0.7917 0.920 0.056 0.016 0.000 0.008
#> GSM907796 1 0.3595 0.7471 0.828 0.000 0.048 0.004 0.120
#> GSM907797 5 0.5929 0.0508 0.428 0.000 0.052 0.024 0.496
#> GSM907798 1 0.3062 0.7656 0.868 0.000 0.048 0.004 0.080
#> GSM907799 1 0.2157 0.7989 0.920 0.036 0.040 0.000 0.004
#> GSM907800 1 0.5378 0.6817 0.708 0.188 0.080 0.008 0.016
#> GSM907803 1 0.2157 0.7988 0.920 0.040 0.036 0.000 0.004
#> GSM907864 4 0.1569 0.7929 0.004 0.008 0.044 0.944 0.000
#> GSM907865 4 0.1579 0.7775 0.000 0.000 0.032 0.944 0.024
#> GSM907868 3 0.3419 0.9467 0.016 0.180 0.804 0.000 0.000
#> GSM907869 5 0.3862 0.7315 0.000 0.000 0.104 0.088 0.808
#> GSM907870 2 0.2377 0.8687 0.000 0.872 0.128 0.000 0.000
#> GSM907861 3 0.3391 0.9472 0.012 0.188 0.800 0.000 0.000
#> GSM907862 3 0.3496 0.9396 0.012 0.200 0.788 0.000 0.000
#> GSM907863 3 0.3496 0.9396 0.012 0.200 0.788 0.000 0.000
#> GSM907866 5 0.4164 0.7331 0.000 0.000 0.120 0.096 0.784
#> GSM907867 3 0.3934 0.8560 0.008 0.276 0.716 0.000 0.000
#> GSM907839 4 0.1569 0.7929 0.004 0.008 0.044 0.944 0.000
#> GSM907840 4 0.0880 0.7843 0.000 0.000 0.032 0.968 0.000
#> GSM907842 4 0.1960 0.7871 0.004 0.020 0.048 0.928 0.000
#> GSM907843 2 0.1608 0.9122 0.000 0.928 0.072 0.000 0.000
#> GSM907845 2 0.4610 0.7217 0.176 0.752 0.060 0.000 0.012
#> GSM907846 1 0.7837 0.2755 0.452 0.308 0.164 0.024 0.052
#> GSM907848 2 0.1525 0.9155 0.012 0.948 0.036 0.000 0.004
#> GSM907851 2 0.3165 0.8253 0.116 0.848 0.036 0.000 0.000
#> GSM907835 2 0.0404 0.9208 0.000 0.988 0.012 0.000 0.000
#> GSM907836 2 0.0510 0.9192 0.000 0.984 0.016 0.000 0.000
#> GSM907837 2 0.0162 0.9147 0.000 0.996 0.004 0.000 0.000
#> GSM907838 2 0.0290 0.9165 0.000 0.992 0.008 0.000 0.000
#> GSM907841 5 0.4164 0.7331 0.000 0.000 0.120 0.096 0.784
#> GSM907844 2 0.1124 0.9226 0.004 0.960 0.036 0.000 0.000
#> GSM907847 2 0.1544 0.9137 0.000 0.932 0.068 0.000 0.000
#> GSM907849 2 0.1877 0.9141 0.012 0.924 0.064 0.000 0.000
#> GSM907850 2 0.0880 0.9234 0.000 0.968 0.032 0.000 0.000
#> GSM907852 2 0.0290 0.9129 0.000 0.992 0.008 0.000 0.000
#> GSM907853 2 0.2597 0.9032 0.024 0.884 0.092 0.000 0.000
#> GSM907807 1 0.5033 0.7154 0.760 0.012 0.112 0.020 0.096
#> GSM907813 4 0.6897 0.4591 0.152 0.000 0.132 0.600 0.116
#> GSM907814 4 0.6897 0.4591 0.152 0.000 0.132 0.600 0.116
#> GSM907816 1 0.2308 0.7985 0.912 0.036 0.048 0.000 0.004
#> GSM907818 1 0.3696 0.7920 0.852 0.056 0.044 0.004 0.044
#> GSM907819 1 0.4684 0.7487 0.804 0.052 0.072 0.024 0.048
#> GSM907820 1 0.5681 0.6601 0.684 0.204 0.080 0.008 0.024
#> GSM907822 1 0.3124 0.7906 0.884 0.028 0.056 0.016 0.016
#> GSM907823 1 0.3818 0.7843 0.848 0.040 0.072 0.020 0.020
#> GSM907808 1 0.4988 0.6955 0.752 0.004 0.128 0.020 0.096
#> GSM907809 1 0.4988 0.6955 0.752 0.004 0.128 0.020 0.096
#> GSM907810 1 0.3844 0.7863 0.836 0.032 0.068 0.000 0.064
#> GSM907811 1 0.2234 0.7989 0.916 0.044 0.036 0.000 0.004
#> GSM907812 1 0.3595 0.7471 0.828 0.000 0.048 0.004 0.120
#> GSM907815 5 0.1608 0.6659 0.000 0.000 0.000 0.072 0.928
#> GSM907817 1 0.5378 0.6817 0.708 0.188 0.080 0.008 0.016
#> GSM907821 1 0.5779 0.6631 0.684 0.196 0.080 0.008 0.032
#> GSM907824 1 0.5779 0.6631 0.684 0.196 0.080 0.008 0.032
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0943 0.9259 0.004 0.004 0.972 0.012 0.004 0.004
#> GSM907859 4 0.2857 0.7652 0.028 0.012 0.056 0.884 0.016 0.004
#> GSM907860 3 0.0547 0.9412 0.000 0.020 0.980 0.000 0.000 0.000
#> GSM907854 3 0.0632 0.9412 0.000 0.024 0.976 0.000 0.000 0.000
#> GSM907855 3 0.0363 0.9385 0.000 0.012 0.988 0.000 0.000 0.000
#> GSM907856 3 0.0622 0.9373 0.000 0.012 0.980 0.008 0.000 0.000
#> GSM907857 3 0.3812 0.6955 0.056 0.000 0.772 0.000 0.004 0.168
#> GSM907825 2 0.2328 0.9165 0.000 0.892 0.056 0.000 0.052 0.000
#> GSM907828 2 0.1692 0.9110 0.000 0.932 0.048 0.008 0.012 0.000
#> GSM907832 2 0.3376 0.8689 0.004 0.816 0.052 0.000 0.128 0.000
#> GSM907833 2 0.2920 0.9067 0.000 0.864 0.080 0.016 0.040 0.000
#> GSM907834 2 0.2263 0.9132 0.000 0.896 0.048 0.000 0.056 0.000
#> GSM907826 2 0.1225 0.9218 0.000 0.952 0.036 0.000 0.012 0.000
#> GSM907827 2 0.2558 0.8945 0.000 0.868 0.104 0.000 0.028 0.000
#> GSM907829 2 0.4298 0.8348 0.076 0.776 0.112 0.000 0.032 0.004
#> GSM907830 4 0.3728 0.6245 0.000 0.152 0.060 0.784 0.004 0.000
#> GSM907831 2 0.2618 0.9103 0.000 0.872 0.076 0.000 0.052 0.000
#> GSM907792 1 0.3446 0.7160 0.692 0.000 0.000 0.000 0.308 0.000
#> GSM907795 1 0.0000 0.6563 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.2527 0.7169 0.832 0.000 0.000 0.000 0.168 0.000
#> GSM907802 5 0.2448 0.8345 0.052 0.064 0.000 0.000 0.884 0.000
#> GSM907804 5 0.3116 0.6842 0.132 0.000 0.004 0.016 0.836 0.012
#> GSM907805 1 0.5747 0.5786 0.548 0.008 0.016 0.056 0.356 0.016
#> GSM907806 1 0.3789 0.6314 0.584 0.000 0.000 0.000 0.416 0.000
#> GSM907793 1 0.0865 0.6763 0.964 0.000 0.000 0.000 0.036 0.000
#> GSM907794 1 0.3971 0.5898 0.548 0.004 0.000 0.000 0.448 0.000
#> GSM907796 1 0.4063 0.6676 0.736 0.000 0.004 0.000 0.208 0.052
#> GSM907797 1 0.5851 0.0336 0.416 0.000 0.004 0.000 0.164 0.416
#> GSM907798 1 0.3398 0.6901 0.768 0.000 0.004 0.000 0.216 0.012
#> GSM907799 1 0.3672 0.6812 0.632 0.000 0.000 0.000 0.368 0.000
#> GSM907800 5 0.2629 0.8279 0.068 0.060 0.000 0.000 0.872 0.000
#> GSM907803 1 0.3706 0.6746 0.620 0.000 0.000 0.000 0.380 0.000
#> GSM907864 4 0.0603 0.8083 0.000 0.004 0.016 0.980 0.000 0.000
#> GSM907865 4 0.0862 0.7969 0.000 0.000 0.004 0.972 0.008 0.016
#> GSM907868 3 0.0603 0.9402 0.004 0.016 0.980 0.000 0.000 0.000
#> GSM907869 6 0.1353 0.9415 0.000 0.000 0.024 0.012 0.012 0.952
#> GSM907870 2 0.2680 0.8711 0.000 0.856 0.124 0.004 0.016 0.000
#> GSM907861 3 0.0632 0.9412 0.000 0.024 0.976 0.000 0.000 0.000
#> GSM907862 3 0.1007 0.9290 0.000 0.044 0.956 0.000 0.000 0.000
#> GSM907863 3 0.1007 0.9290 0.000 0.044 0.956 0.000 0.000 0.000
#> GSM907866 6 0.1908 0.9463 0.000 0.000 0.044 0.020 0.012 0.924
#> GSM907867 3 0.2260 0.8172 0.000 0.140 0.860 0.000 0.000 0.000
#> GSM907839 4 0.0603 0.8083 0.000 0.004 0.016 0.980 0.000 0.000
#> GSM907840 4 0.0146 0.8030 0.000 0.000 0.000 0.996 0.004 0.000
#> GSM907842 4 0.1003 0.8037 0.000 0.016 0.020 0.964 0.000 0.000
#> GSM907843 2 0.1434 0.9116 0.000 0.940 0.048 0.000 0.012 0.000
#> GSM907845 2 0.4495 0.7598 0.156 0.744 0.064 0.000 0.036 0.000
#> GSM907846 5 0.7361 0.3471 0.088 0.256 0.052 0.020 0.516 0.068
#> GSM907848 2 0.2325 0.9136 0.000 0.892 0.048 0.000 0.060 0.000
#> GSM907851 2 0.2971 0.8402 0.116 0.848 0.024 0.000 0.012 0.000
#> GSM907835 2 0.1320 0.9199 0.000 0.948 0.016 0.000 0.036 0.000
#> GSM907836 2 0.1480 0.9187 0.000 0.940 0.020 0.000 0.040 0.000
#> GSM907837 2 0.1007 0.9125 0.000 0.956 0.000 0.000 0.044 0.000
#> GSM907838 2 0.1082 0.9148 0.000 0.956 0.004 0.000 0.040 0.000
#> GSM907841 6 0.1908 0.9463 0.000 0.000 0.044 0.020 0.012 0.924
#> GSM907844 2 0.1863 0.9207 0.000 0.920 0.044 0.000 0.036 0.000
#> GSM907847 2 0.1367 0.9118 0.000 0.944 0.044 0.000 0.012 0.000
#> GSM907849 2 0.1726 0.9119 0.012 0.932 0.044 0.000 0.012 0.000
#> GSM907850 2 0.1572 0.9219 0.000 0.936 0.028 0.000 0.036 0.000
#> GSM907852 2 0.1141 0.9111 0.000 0.948 0.000 0.000 0.052 0.000
#> GSM907853 2 0.2611 0.9037 0.016 0.876 0.092 0.000 0.016 0.000
#> GSM907807 1 0.1387 0.6959 0.932 0.000 0.000 0.000 0.068 0.000
#> GSM907813 4 0.4619 0.5047 0.396 0.000 0.004 0.572 0.012 0.016
#> GSM907814 4 0.4619 0.5047 0.396 0.000 0.004 0.572 0.012 0.016
#> GSM907816 1 0.3699 0.7000 0.660 0.004 0.000 0.000 0.336 0.000
#> GSM907818 1 0.4411 0.6067 0.576 0.012 0.000 0.000 0.400 0.012
#> GSM907819 5 0.3894 0.4384 0.240 0.000 0.004 0.016 0.732 0.008
#> GSM907820 5 0.2554 0.8312 0.048 0.076 0.000 0.000 0.876 0.000
#> GSM907822 1 0.3390 0.7120 0.704 0.000 0.000 0.000 0.296 0.000
#> GSM907823 1 0.3564 0.7107 0.724 0.012 0.000 0.000 0.264 0.000
#> GSM907808 1 0.0632 0.6739 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907809 1 0.0632 0.6739 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907810 1 0.3151 0.7300 0.748 0.000 0.000 0.000 0.252 0.000
#> GSM907811 1 0.3727 0.6716 0.612 0.000 0.000 0.000 0.388 0.000
#> GSM907812 1 0.4063 0.6676 0.736 0.000 0.004 0.000 0.208 0.052
#> GSM907815 6 0.1863 0.8742 0.044 0.000 0.000 0.000 0.036 0.920
#> GSM907817 5 0.2629 0.8279 0.068 0.060 0.000 0.000 0.872 0.000
#> GSM907821 5 0.2442 0.8353 0.048 0.068 0.000 0.000 0.884 0.000
#> GSM907824 5 0.2442 0.8353 0.048 0.068 0.000 0.000 0.884 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
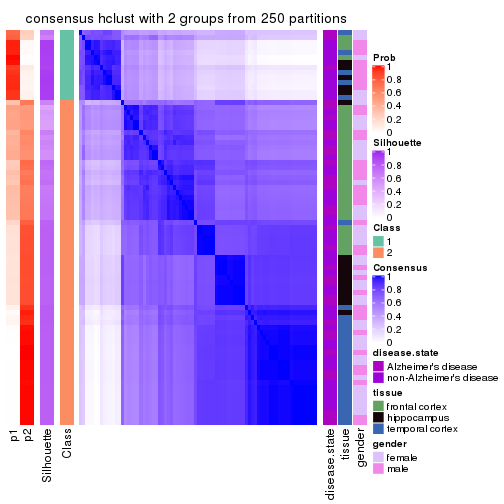
consensus_heatmap(res, k = 3)
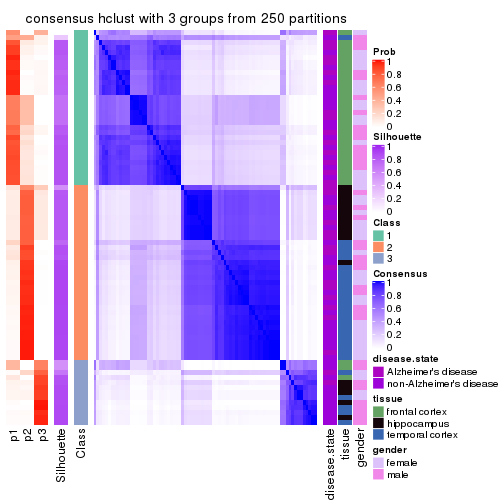
consensus_heatmap(res, k = 4)
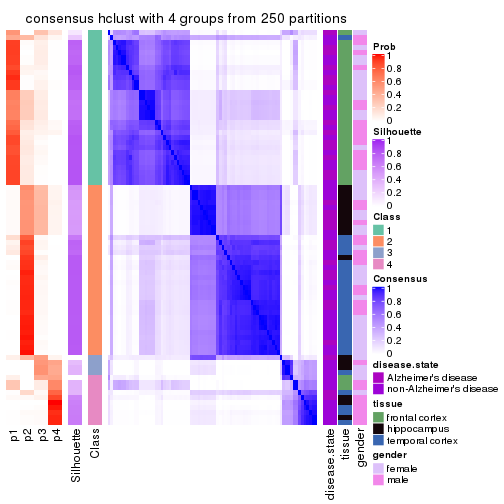
consensus_heatmap(res, k = 5)
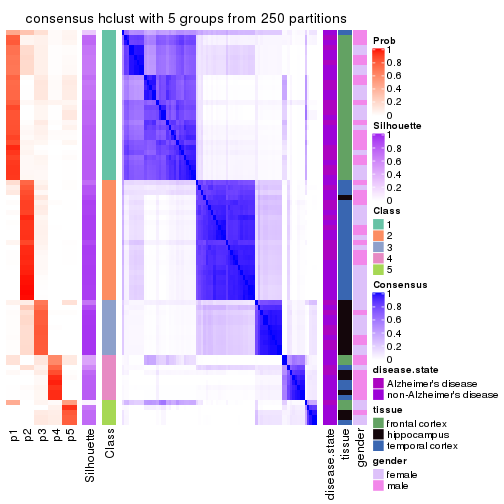
consensus_heatmap(res, k = 6)
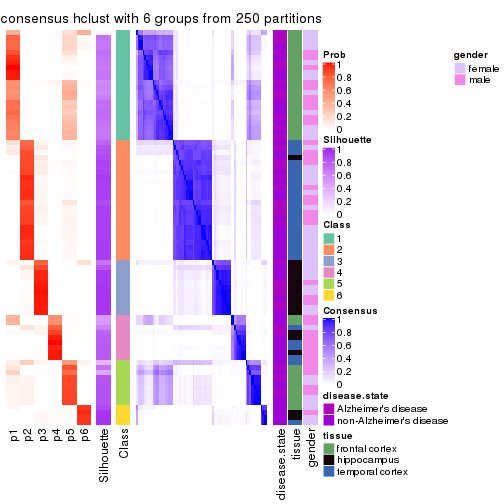
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
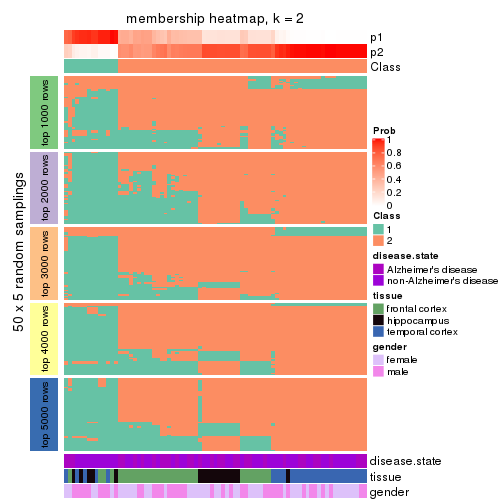
membership_heatmap(res, k = 3)
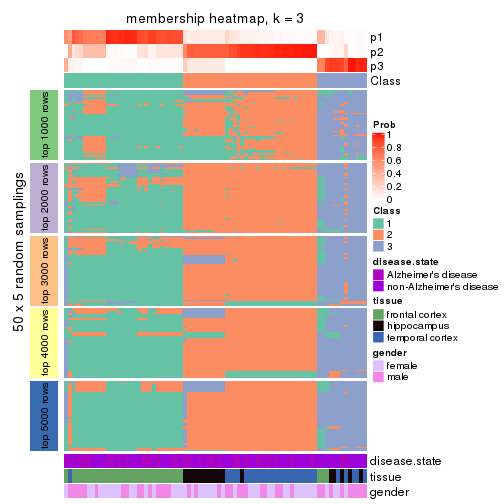
membership_heatmap(res, k = 4)
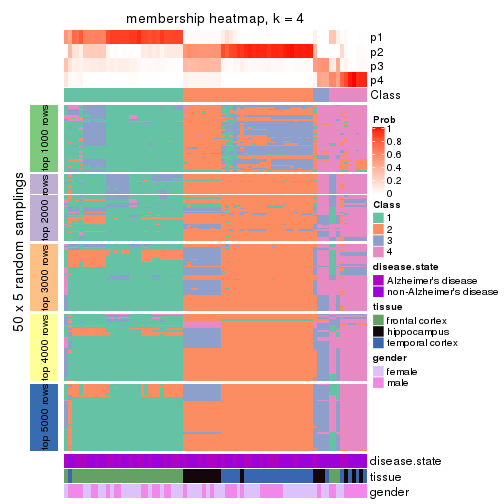
membership_heatmap(res, k = 5)
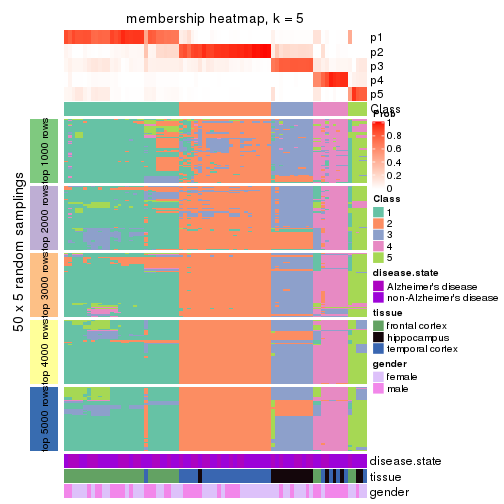
membership_heatmap(res, k = 6)
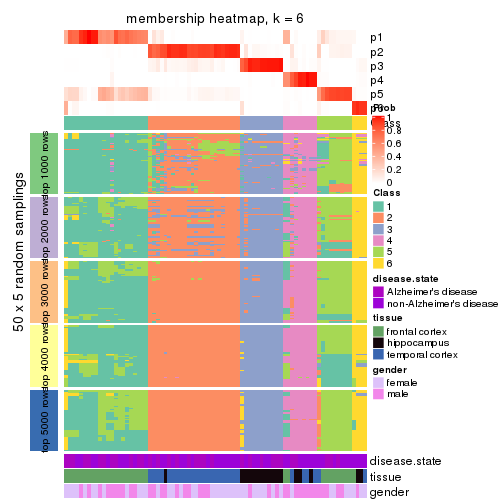
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
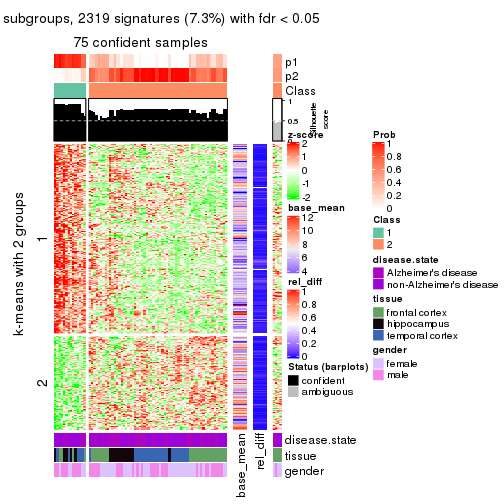
get_signatures(res, k = 3)
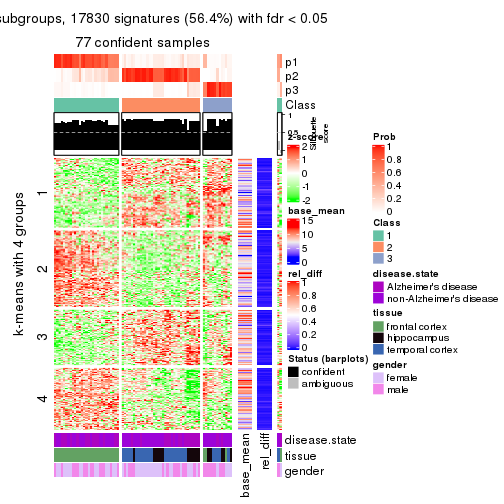
get_signatures(res, k = 4)
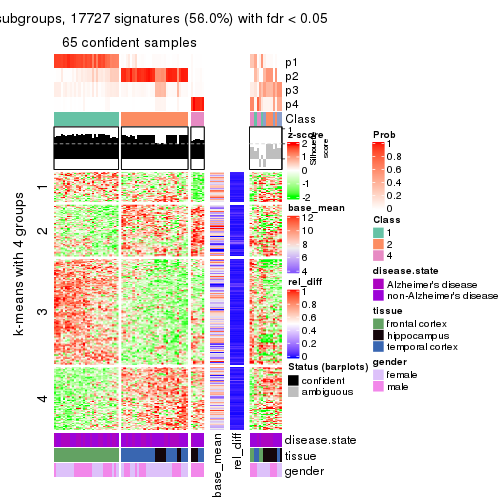
get_signatures(res, k = 5)
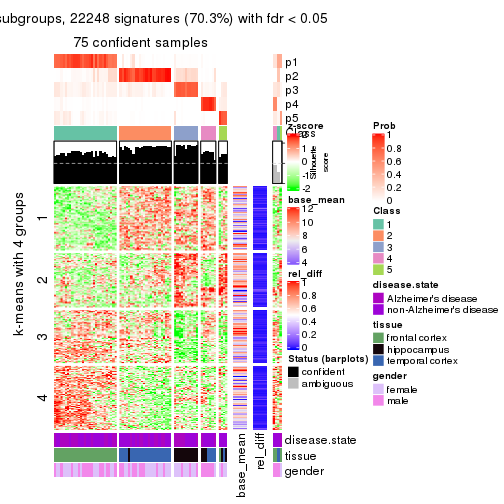
get_signatures(res, k = 6)
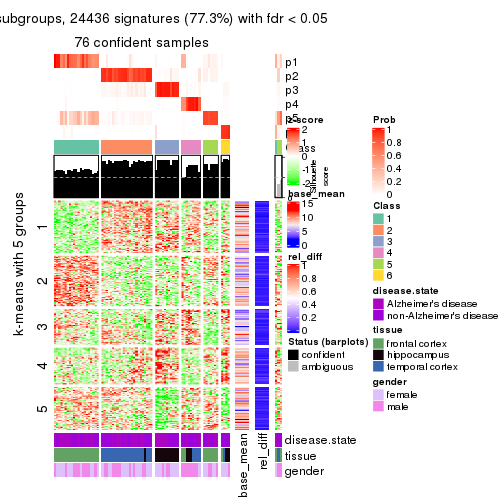
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
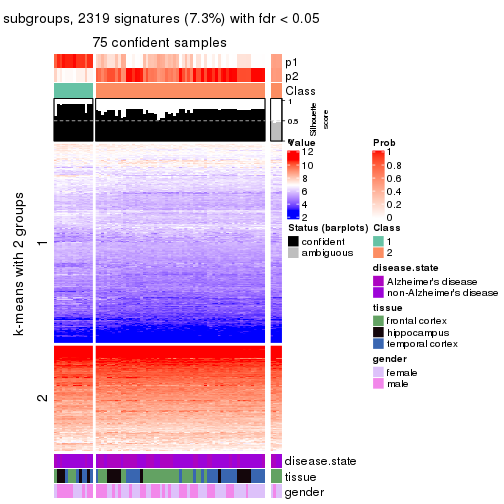
get_signatures(res, k = 3, scale_rows = FALSE)
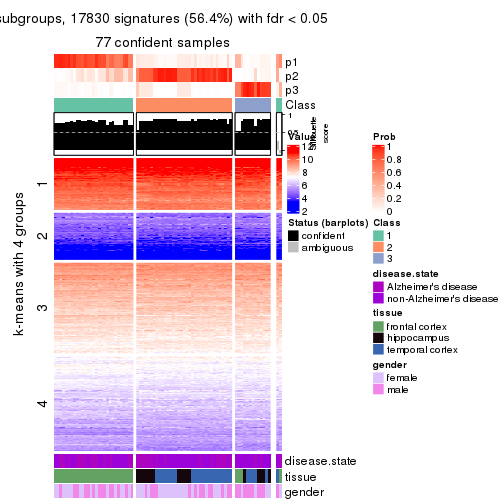
get_signatures(res, k = 4, scale_rows = FALSE)
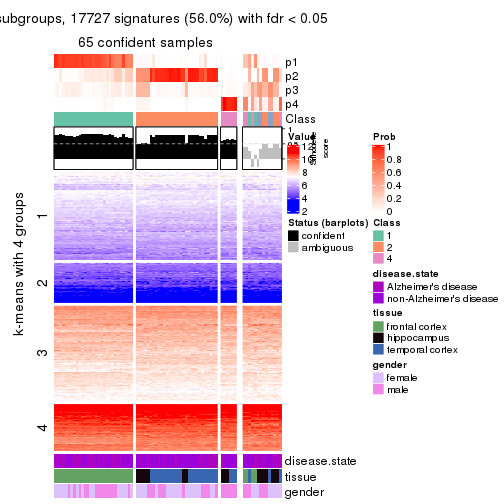
get_signatures(res, k = 5, scale_rows = FALSE)
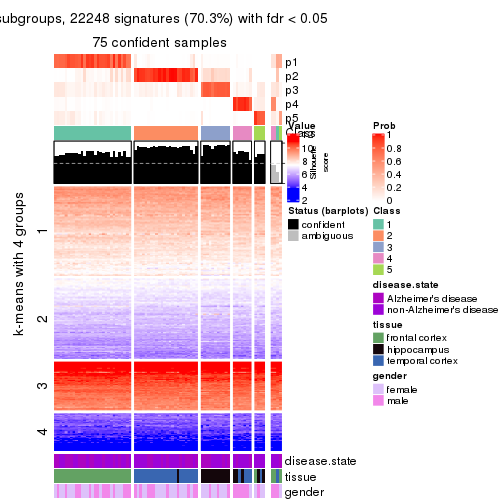
get_signatures(res, k = 6, scale_rows = FALSE)
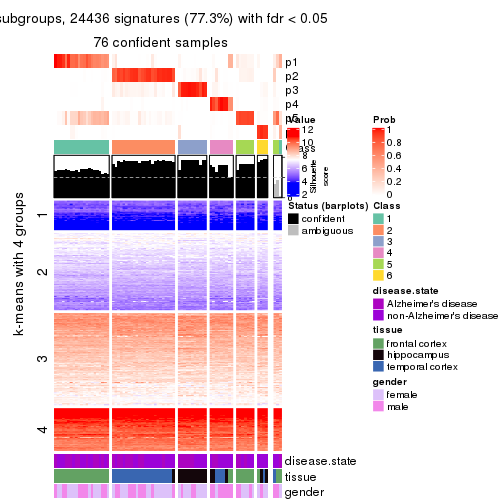
Compare the overlap of signatures from different k:
compare_signatures(res)
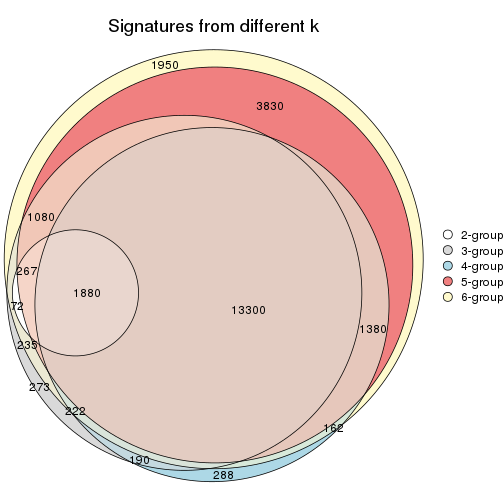
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
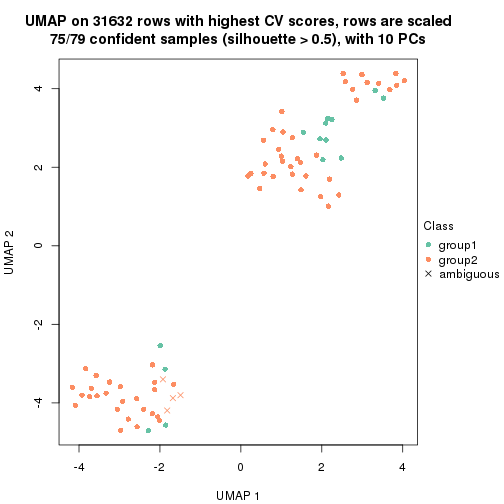
dimension_reduction(res, k = 3, method = "UMAP")
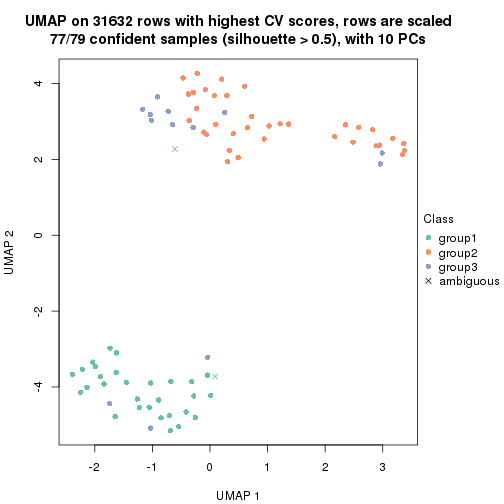
dimension_reduction(res, k = 4, method = "UMAP")
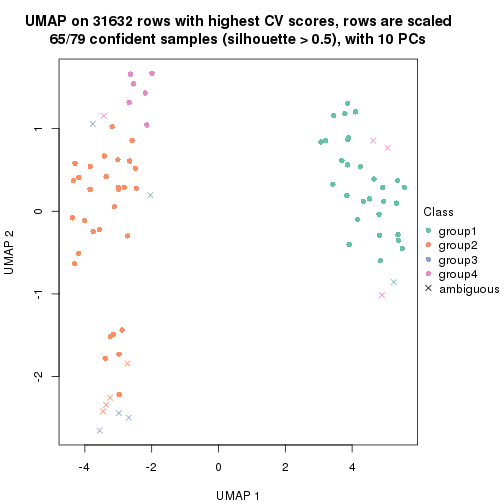
dimension_reduction(res, k = 5, method = "UMAP")
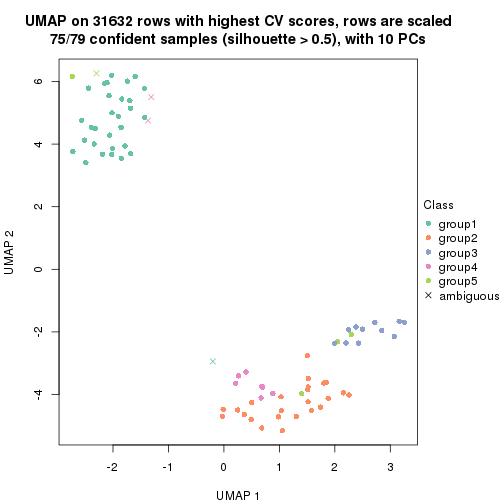
dimension_reduction(res, k = 6, method = "UMAP")
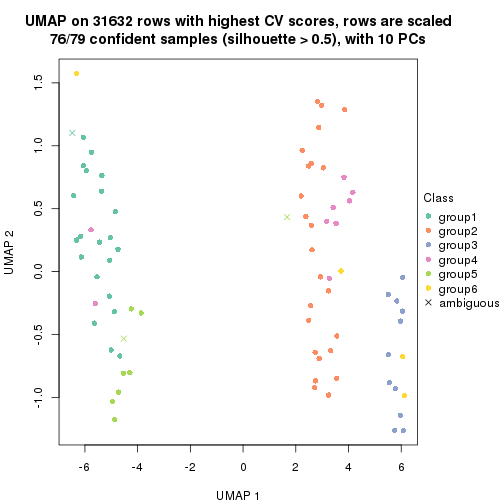
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
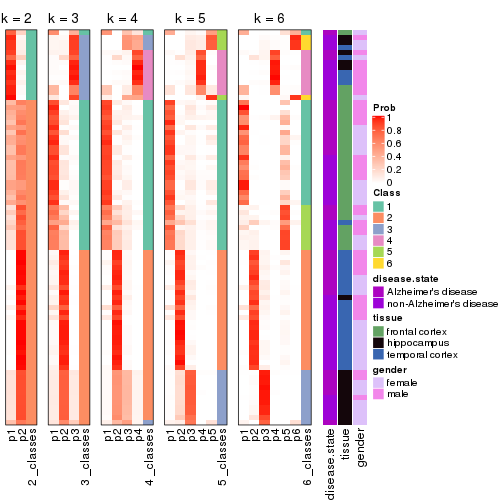
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:hclust 75 0.204 4.10e-01 0.2910 2
#> CV:hclust 77 0.121 4.38e-14 0.1378 3
#> CV:hclust 65 0.312 5.44e-14 0.0179 4
#> CV:hclust 75 0.308 8.94e-23 0.1384 5
#> CV:hclust 76 0.288 1.30e-20 0.1029 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "kmeans"]
# you can also extract it by
# res = res_list["CV:kmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'kmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
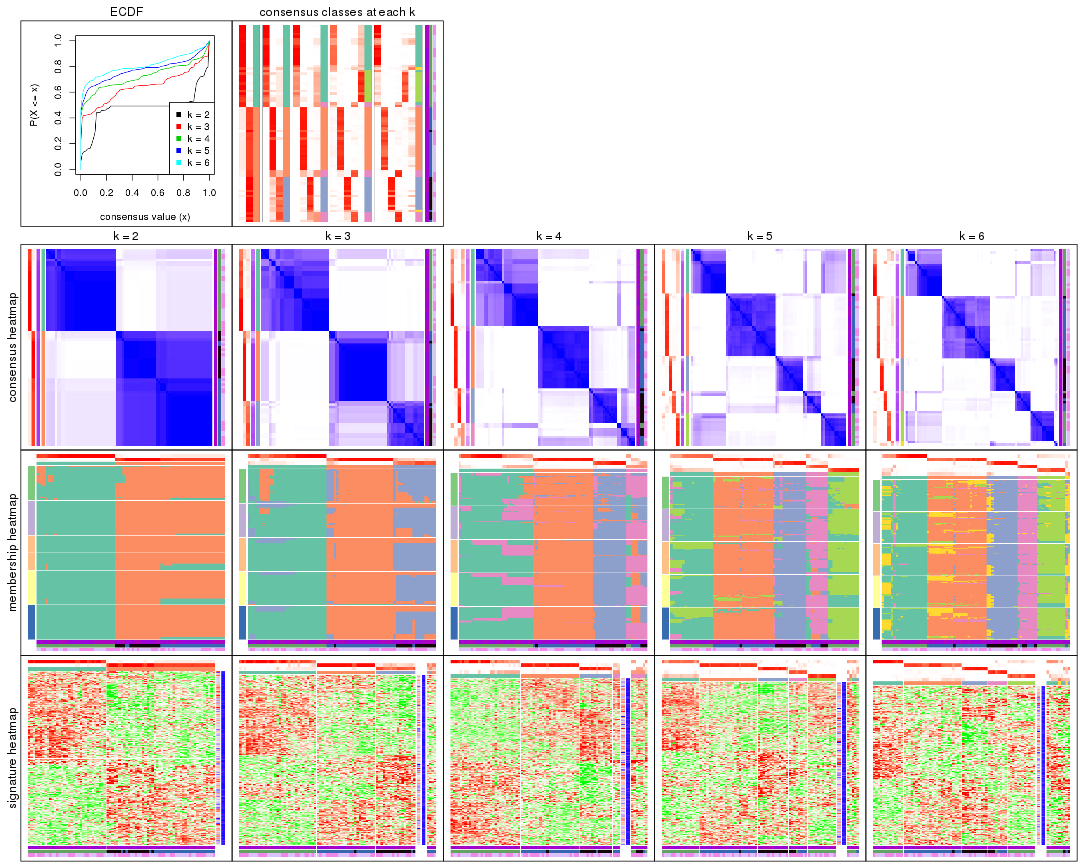
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
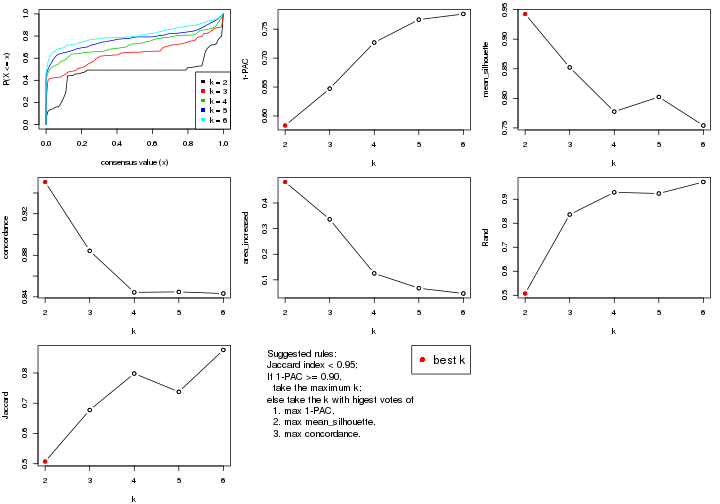
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.584 0.943 0.951 0.4820 0.507 0.507
#> 3 3 0.647 0.852 0.884 0.3361 0.836 0.678
#> 4 4 0.727 0.778 0.844 0.1251 0.929 0.798
#> 5 5 0.766 0.802 0.845 0.0674 0.924 0.738
#> 6 6 0.776 0.754 0.843 0.0467 0.972 0.876
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.923 0.000 1.000
#> GSM907859 2 0.2603 0.903 0.044 0.956
#> GSM907860 2 0.0376 0.925 0.004 0.996
#> GSM907854 2 0.0376 0.925 0.004 0.996
#> GSM907855 2 0.0000 0.923 0.000 1.000
#> GSM907856 2 0.0000 0.923 0.000 1.000
#> GSM907857 2 0.4562 0.865 0.096 0.904
#> GSM907825 2 0.5059 0.942 0.112 0.888
#> GSM907828 2 0.4815 0.942 0.104 0.896
#> GSM907832 2 0.5059 0.942 0.112 0.888
#> GSM907833 2 0.5059 0.942 0.112 0.888
#> GSM907834 2 0.5059 0.942 0.112 0.888
#> GSM907826 2 0.5059 0.942 0.112 0.888
#> GSM907827 2 0.4431 0.942 0.092 0.908
#> GSM907829 2 0.5178 0.939 0.116 0.884
#> GSM907830 2 0.3879 0.941 0.076 0.924
#> GSM907831 2 0.5059 0.942 0.112 0.888
#> GSM907792 1 0.0000 0.977 1.000 0.000
#> GSM907795 1 0.0000 0.977 1.000 0.000
#> GSM907801 1 0.0000 0.977 1.000 0.000
#> GSM907802 1 0.5178 0.871 0.884 0.116
#> GSM907804 1 0.0376 0.975 0.996 0.004
#> GSM907805 1 0.0376 0.975 0.996 0.004
#> GSM907806 1 0.0000 0.977 1.000 0.000
#> GSM907793 1 0.0376 0.975 0.996 0.004
#> GSM907794 1 0.0000 0.977 1.000 0.000
#> GSM907796 1 0.0000 0.977 1.000 0.000
#> GSM907797 1 0.0376 0.975 0.996 0.004
#> GSM907798 1 0.0000 0.977 1.000 0.000
#> GSM907799 1 0.0000 0.977 1.000 0.000
#> GSM907800 1 0.2423 0.948 0.960 0.040
#> GSM907803 1 0.0000 0.977 1.000 0.000
#> GSM907864 2 0.0000 0.923 0.000 1.000
#> GSM907865 2 0.4562 0.864 0.096 0.904
#> GSM907868 2 0.0376 0.925 0.004 0.996
#> GSM907869 2 0.4690 0.861 0.100 0.900
#> GSM907870 2 0.0376 0.925 0.004 0.996
#> GSM907861 2 0.0376 0.925 0.004 0.996
#> GSM907862 2 0.0376 0.925 0.004 0.996
#> GSM907863 2 0.0376 0.925 0.004 0.996
#> GSM907866 2 0.0000 0.923 0.000 1.000
#> GSM907867 2 0.0376 0.925 0.004 0.996
#> GSM907839 2 0.3879 0.941 0.076 0.924
#> GSM907840 2 0.0000 0.923 0.000 1.000
#> GSM907842 2 0.3879 0.941 0.076 0.924
#> GSM907843 2 0.5059 0.942 0.112 0.888
#> GSM907845 2 0.5059 0.942 0.112 0.888
#> GSM907846 2 0.4298 0.941 0.088 0.912
#> GSM907848 2 0.5059 0.942 0.112 0.888
#> GSM907851 2 0.5059 0.942 0.112 0.888
#> GSM907835 2 0.5059 0.942 0.112 0.888
#> GSM907836 2 0.5059 0.942 0.112 0.888
#> GSM907837 2 0.5059 0.942 0.112 0.888
#> GSM907838 2 0.5059 0.942 0.112 0.888
#> GSM907841 2 0.0000 0.923 0.000 1.000
#> GSM907844 2 0.5059 0.942 0.112 0.888
#> GSM907847 2 0.5059 0.942 0.112 0.888
#> GSM907849 2 0.5059 0.942 0.112 0.888
#> GSM907850 2 0.5059 0.942 0.112 0.888
#> GSM907852 2 0.5059 0.942 0.112 0.888
#> GSM907853 2 0.5059 0.942 0.112 0.888
#> GSM907807 1 0.0000 0.977 1.000 0.000
#> GSM907813 1 0.1633 0.961 0.976 0.024
#> GSM907814 1 0.1633 0.961 0.976 0.024
#> GSM907816 1 0.0000 0.977 1.000 0.000
#> GSM907818 1 0.0000 0.977 1.000 0.000
#> GSM907819 1 0.0000 0.977 1.000 0.000
#> GSM907820 1 0.5178 0.871 0.884 0.116
#> GSM907822 1 0.0000 0.977 1.000 0.000
#> GSM907823 1 0.0000 0.977 1.000 0.000
#> GSM907808 1 0.0000 0.977 1.000 0.000
#> GSM907809 1 0.0000 0.977 1.000 0.000
#> GSM907810 1 0.0000 0.977 1.000 0.000
#> GSM907811 1 0.0000 0.977 1.000 0.000
#> GSM907812 1 0.0000 0.977 1.000 0.000
#> GSM907815 1 0.4431 0.894 0.908 0.092
#> GSM907817 1 0.2423 0.948 0.960 0.040
#> GSM907821 1 0.4161 0.907 0.916 0.084
#> GSM907824 1 0.4815 0.885 0.896 0.104
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.4796 0.872 0.000 0.220 0.780
#> GSM907859 3 0.3826 0.837 0.008 0.124 0.868
#> GSM907860 3 0.5216 0.860 0.000 0.260 0.740
#> GSM907854 3 0.5529 0.832 0.000 0.296 0.704
#> GSM907855 3 0.4654 0.873 0.000 0.208 0.792
#> GSM907856 3 0.4235 0.869 0.000 0.176 0.824
#> GSM907857 3 0.4634 0.865 0.012 0.164 0.824
#> GSM907825 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907828 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907832 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907833 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907834 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907826 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907827 2 0.0475 0.929 0.004 0.992 0.004
#> GSM907829 2 0.0848 0.924 0.008 0.984 0.008
#> GSM907830 2 0.5733 0.434 0.000 0.676 0.324
#> GSM907831 2 0.0475 0.929 0.004 0.992 0.004
#> GSM907792 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907802 1 0.7923 0.702 0.652 0.228 0.120
#> GSM907804 1 0.3340 0.894 0.880 0.000 0.120
#> GSM907805 1 0.0237 0.911 0.996 0.000 0.004
#> GSM907806 1 0.3340 0.894 0.880 0.000 0.120
#> GSM907793 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907794 1 0.3340 0.894 0.880 0.000 0.120
#> GSM907796 1 0.1860 0.908 0.948 0.000 0.052
#> GSM907797 1 0.1860 0.908 0.948 0.000 0.052
#> GSM907798 1 0.1860 0.908 0.948 0.000 0.052
#> GSM907799 1 0.0237 0.911 0.996 0.000 0.004
#> GSM907800 1 0.5695 0.852 0.804 0.076 0.120
#> GSM907803 1 0.2356 0.902 0.928 0.000 0.072
#> GSM907864 3 0.3551 0.841 0.000 0.132 0.868
#> GSM907865 3 0.3918 0.834 0.012 0.120 0.868
#> GSM907868 3 0.5254 0.858 0.000 0.264 0.736
#> GSM907869 3 0.3695 0.834 0.012 0.108 0.880
#> GSM907870 2 0.4002 0.710 0.000 0.840 0.160
#> GSM907861 3 0.6154 0.641 0.000 0.408 0.592
#> GSM907862 3 0.5397 0.848 0.000 0.280 0.720
#> GSM907863 3 0.5397 0.848 0.000 0.280 0.720
#> GSM907866 3 0.4235 0.869 0.000 0.176 0.824
#> GSM907867 3 0.5560 0.828 0.000 0.300 0.700
#> GSM907839 2 0.5859 0.392 0.000 0.656 0.344
#> GSM907840 3 0.6204 0.421 0.000 0.424 0.576
#> GSM907842 2 0.5859 0.392 0.000 0.656 0.344
#> GSM907843 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907845 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907846 2 0.4291 0.737 0.008 0.840 0.152
#> GSM907848 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907851 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907835 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907836 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907837 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907838 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907841 3 0.5465 0.797 0.000 0.288 0.712
#> GSM907844 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907847 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907849 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907850 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907852 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907853 2 0.0424 0.933 0.008 0.992 0.000
#> GSM907807 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907813 1 0.4033 0.817 0.856 0.008 0.136
#> GSM907814 1 0.4033 0.817 0.856 0.008 0.136
#> GSM907816 1 0.0237 0.911 0.996 0.000 0.004
#> GSM907818 1 0.3340 0.894 0.880 0.000 0.120
#> GSM907819 1 0.3267 0.896 0.884 0.000 0.116
#> GSM907820 1 0.7997 0.692 0.644 0.236 0.120
#> GSM907822 1 0.0237 0.911 0.996 0.000 0.004
#> GSM907823 1 0.0237 0.911 0.996 0.000 0.004
#> GSM907808 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.911 1.000 0.000 0.000
#> GSM907811 1 0.2448 0.902 0.924 0.000 0.076
#> GSM907812 1 0.1860 0.908 0.948 0.000 0.052
#> GSM907815 1 0.5896 0.682 0.700 0.008 0.292
#> GSM907817 1 0.5863 0.846 0.796 0.084 0.120
#> GSM907821 1 0.7844 0.712 0.660 0.220 0.120
#> GSM907824 1 0.7884 0.707 0.656 0.224 0.120
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0524 0.894 0.000 0.008 0.988 0.004
#> GSM907859 4 0.5277 0.275 0.000 0.008 0.460 0.532
#> GSM907860 3 0.1297 0.896 0.000 0.020 0.964 0.016
#> GSM907854 3 0.2125 0.870 0.000 0.076 0.920 0.004
#> GSM907855 3 0.0657 0.895 0.000 0.012 0.984 0.004
#> GSM907856 3 0.0927 0.890 0.000 0.008 0.976 0.016
#> GSM907857 3 0.0779 0.887 0.000 0.004 0.980 0.016
#> GSM907825 2 0.0927 0.962 0.000 0.976 0.008 0.016
#> GSM907828 2 0.1151 0.961 0.000 0.968 0.008 0.024
#> GSM907832 2 0.1004 0.962 0.000 0.972 0.004 0.024
#> GSM907833 2 0.1004 0.962 0.000 0.972 0.004 0.024
#> GSM907834 2 0.0927 0.962 0.000 0.976 0.008 0.016
#> GSM907826 2 0.0804 0.963 0.000 0.980 0.012 0.008
#> GSM907827 2 0.0657 0.964 0.000 0.984 0.012 0.004
#> GSM907829 2 0.0779 0.961 0.000 0.980 0.004 0.016
#> GSM907830 4 0.6726 0.490 0.000 0.364 0.100 0.536
#> GSM907831 2 0.0657 0.964 0.000 0.984 0.004 0.012
#> GSM907792 1 0.0188 0.769 0.996 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0188 0.769 0.996 0.000 0.000 0.004
#> GSM907802 1 0.7244 0.603 0.452 0.124 0.004 0.420
#> GSM907804 1 0.4967 0.688 0.548 0.000 0.000 0.452
#> GSM907805 1 0.1022 0.772 0.968 0.000 0.000 0.032
#> GSM907806 1 0.4855 0.716 0.600 0.000 0.000 0.400
#> GSM907793 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907794 1 0.4877 0.713 0.592 0.000 0.000 0.408
#> GSM907796 1 0.3105 0.768 0.856 0.000 0.004 0.140
#> GSM907797 1 0.3157 0.767 0.852 0.000 0.004 0.144
#> GSM907798 1 0.3105 0.768 0.856 0.000 0.004 0.140
#> GSM907799 1 0.0817 0.773 0.976 0.000 0.000 0.024
#> GSM907800 1 0.5716 0.692 0.552 0.028 0.000 0.420
#> GSM907803 1 0.4250 0.735 0.724 0.000 0.000 0.276
#> GSM907864 4 0.5353 0.317 0.000 0.012 0.432 0.556
#> GSM907865 4 0.5277 0.275 0.000 0.008 0.460 0.532
#> GSM907868 3 0.0779 0.898 0.000 0.016 0.980 0.004
#> GSM907869 3 0.3024 0.728 0.000 0.000 0.852 0.148
#> GSM907870 2 0.3787 0.815 0.000 0.840 0.124 0.036
#> GSM907861 3 0.2918 0.815 0.000 0.116 0.876 0.008
#> GSM907862 3 0.2413 0.881 0.000 0.064 0.916 0.020
#> GSM907863 3 0.2489 0.877 0.000 0.068 0.912 0.020
#> GSM907866 3 0.0804 0.891 0.000 0.008 0.980 0.012
#> GSM907867 3 0.2198 0.876 0.000 0.072 0.920 0.008
#> GSM907839 4 0.6764 0.544 0.000 0.332 0.112 0.556
#> GSM907840 4 0.7153 0.521 0.000 0.196 0.248 0.556
#> GSM907842 4 0.6778 0.539 0.000 0.336 0.112 0.552
#> GSM907843 2 0.1151 0.961 0.000 0.968 0.008 0.024
#> GSM907845 2 0.1004 0.962 0.000 0.972 0.004 0.024
#> GSM907846 2 0.3894 0.804 0.000 0.844 0.068 0.088
#> GSM907848 2 0.1004 0.962 0.000 0.972 0.004 0.024
#> GSM907851 2 0.1151 0.961 0.000 0.968 0.008 0.024
#> GSM907835 2 0.0657 0.964 0.000 0.984 0.004 0.012
#> GSM907836 2 0.0937 0.962 0.000 0.976 0.012 0.012
#> GSM907837 2 0.0937 0.962 0.000 0.976 0.012 0.012
#> GSM907838 2 0.1059 0.962 0.000 0.972 0.012 0.016
#> GSM907841 3 0.5676 0.533 0.000 0.136 0.720 0.144
#> GSM907844 2 0.0524 0.964 0.000 0.988 0.004 0.008
#> GSM907847 2 0.0779 0.964 0.000 0.980 0.004 0.016
#> GSM907849 2 0.1004 0.962 0.000 0.972 0.004 0.024
#> GSM907850 2 0.0895 0.966 0.000 0.976 0.004 0.020
#> GSM907852 2 0.0657 0.964 0.000 0.984 0.004 0.012
#> GSM907853 2 0.0707 0.964 0.000 0.980 0.000 0.020
#> GSM907807 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907813 4 0.5290 0.284 0.476 0.000 0.008 0.516
#> GSM907814 4 0.5163 0.276 0.480 0.000 0.004 0.516
#> GSM907816 1 0.0188 0.769 0.996 0.000 0.000 0.004
#> GSM907818 1 0.4866 0.715 0.596 0.000 0.000 0.404
#> GSM907819 1 0.4817 0.721 0.612 0.000 0.000 0.388
#> GSM907820 1 0.7244 0.603 0.452 0.124 0.004 0.420
#> GSM907822 1 0.0188 0.769 0.996 0.000 0.000 0.004
#> GSM907823 1 0.0188 0.769 0.996 0.000 0.000 0.004
#> GSM907808 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.768 1.000 0.000 0.000 0.000
#> GSM907811 1 0.4454 0.731 0.692 0.000 0.000 0.308
#> GSM907812 1 0.3105 0.768 0.856 0.000 0.004 0.140
#> GSM907815 1 0.6821 0.418 0.592 0.000 0.152 0.256
#> GSM907817 1 0.5881 0.687 0.544 0.036 0.000 0.420
#> GSM907821 1 0.7167 0.613 0.460 0.116 0.004 0.420
#> GSM907824 1 0.7206 0.608 0.456 0.120 0.004 0.420
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0566 0.8877 0.000 0.004 0.984 0.012 0.000
#> GSM907859 4 0.2891 0.7302 0.000 0.000 0.176 0.824 0.000
#> GSM907860 3 0.0932 0.8875 0.000 0.004 0.972 0.020 0.004
#> GSM907854 3 0.0955 0.8847 0.000 0.028 0.968 0.004 0.000
#> GSM907855 3 0.0671 0.8879 0.000 0.004 0.980 0.016 0.000
#> GSM907856 3 0.0671 0.8879 0.000 0.004 0.980 0.016 0.000
#> GSM907857 3 0.2804 0.8336 0.068 0.000 0.884 0.044 0.004
#> GSM907825 2 0.2637 0.9250 0.060 0.900 0.004 0.008 0.028
#> GSM907828 2 0.1622 0.9308 0.016 0.948 0.004 0.028 0.004
#> GSM907832 2 0.1989 0.9281 0.020 0.932 0.000 0.032 0.016
#> GSM907833 2 0.1989 0.9281 0.020 0.932 0.000 0.032 0.016
#> GSM907834 2 0.2654 0.9269 0.056 0.900 0.004 0.008 0.032
#> GSM907826 2 0.1788 0.9287 0.056 0.932 0.008 0.000 0.004
#> GSM907827 2 0.1285 0.9368 0.036 0.956 0.004 0.000 0.004
#> GSM907829 2 0.2190 0.9226 0.016 0.928 0.008 0.028 0.020
#> GSM907830 4 0.3973 0.7354 0.008 0.164 0.036 0.792 0.000
#> GSM907831 2 0.2549 0.9258 0.060 0.904 0.004 0.008 0.024
#> GSM907792 1 0.3508 0.8313 0.748 0.000 0.000 0.000 0.252
#> GSM907795 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907801 1 0.3508 0.8313 0.748 0.000 0.000 0.000 0.252
#> GSM907802 5 0.0880 0.8648 0.000 0.032 0.000 0.000 0.968
#> GSM907804 5 0.1469 0.8619 0.036 0.000 0.000 0.016 0.948
#> GSM907805 1 0.4147 0.7640 0.676 0.000 0.000 0.008 0.316
#> GSM907806 5 0.1851 0.8335 0.088 0.000 0.000 0.000 0.912
#> GSM907793 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907794 5 0.1270 0.8606 0.052 0.000 0.000 0.000 0.948
#> GSM907796 1 0.6198 0.5301 0.480 0.000 0.008 0.108 0.404
#> GSM907797 1 0.6271 0.4782 0.508 0.000 0.008 0.124 0.360
#> GSM907798 1 0.6198 0.5301 0.480 0.000 0.008 0.108 0.404
#> GSM907799 1 0.3636 0.8209 0.728 0.000 0.000 0.000 0.272
#> GSM907800 5 0.0771 0.8723 0.004 0.020 0.000 0.000 0.976
#> GSM907803 5 0.4101 0.1936 0.372 0.000 0.000 0.000 0.628
#> GSM907864 4 0.2605 0.7496 0.000 0.000 0.148 0.852 0.000
#> GSM907865 4 0.2891 0.7302 0.000 0.000 0.176 0.824 0.000
#> GSM907868 3 0.0613 0.8897 0.000 0.008 0.984 0.004 0.004
#> GSM907869 3 0.5535 0.6159 0.124 0.000 0.676 0.188 0.012
#> GSM907870 2 0.4772 0.7801 0.052 0.764 0.152 0.028 0.004
#> GSM907861 3 0.1662 0.8642 0.004 0.056 0.936 0.000 0.004
#> GSM907862 3 0.1679 0.8831 0.012 0.020 0.948 0.016 0.004
#> GSM907863 3 0.1679 0.8831 0.012 0.020 0.948 0.016 0.004
#> GSM907866 3 0.3529 0.8094 0.120 0.004 0.836 0.036 0.004
#> GSM907867 3 0.1365 0.8768 0.004 0.040 0.952 0.000 0.004
#> GSM907839 4 0.3165 0.7718 0.000 0.116 0.036 0.848 0.000
#> GSM907840 4 0.3234 0.7774 0.000 0.064 0.084 0.852 0.000
#> GSM907842 4 0.3309 0.7676 0.000 0.128 0.036 0.836 0.000
#> GSM907843 2 0.1748 0.9303 0.016 0.944 0.004 0.028 0.008
#> GSM907845 2 0.2522 0.9217 0.028 0.912 0.004 0.032 0.024
#> GSM907846 2 0.4152 0.8385 0.028 0.824 0.028 0.100 0.020
#> GSM907848 2 0.1989 0.9281 0.020 0.932 0.000 0.032 0.016
#> GSM907851 2 0.1597 0.9317 0.020 0.948 0.000 0.024 0.008
#> GSM907835 2 0.2246 0.9301 0.048 0.920 0.004 0.008 0.020
#> GSM907836 2 0.1717 0.9300 0.052 0.936 0.008 0.000 0.004
#> GSM907837 2 0.2238 0.9233 0.064 0.912 0.004 0.000 0.020
#> GSM907838 2 0.2426 0.9225 0.064 0.908 0.008 0.004 0.016
#> GSM907841 3 0.7604 0.0988 0.144 0.064 0.432 0.352 0.008
#> GSM907844 2 0.2005 0.9275 0.056 0.924 0.004 0.000 0.016
#> GSM907847 2 0.1560 0.9315 0.020 0.948 0.000 0.028 0.004
#> GSM907849 2 0.1372 0.9324 0.016 0.956 0.000 0.024 0.004
#> GSM907850 2 0.1179 0.9344 0.016 0.964 0.000 0.016 0.004
#> GSM907852 2 0.2005 0.9265 0.056 0.924 0.004 0.000 0.016
#> GSM907853 2 0.1393 0.9335 0.008 0.956 0.000 0.024 0.012
#> GSM907807 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907813 4 0.3838 0.5996 0.280 0.000 0.000 0.716 0.004
#> GSM907814 4 0.4452 0.1543 0.496 0.000 0.000 0.500 0.004
#> GSM907816 1 0.3766 0.8212 0.728 0.000 0.000 0.004 0.268
#> GSM907818 5 0.1830 0.8487 0.068 0.000 0.000 0.008 0.924
#> GSM907819 5 0.1830 0.8517 0.068 0.000 0.000 0.008 0.924
#> GSM907820 5 0.1281 0.8517 0.012 0.032 0.000 0.000 0.956
#> GSM907822 1 0.3766 0.8212 0.728 0.000 0.000 0.004 0.268
#> GSM907823 1 0.3741 0.8203 0.732 0.000 0.000 0.004 0.264
#> GSM907808 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907809 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907810 1 0.3480 0.8324 0.752 0.000 0.000 0.000 0.248
#> GSM907811 5 0.3395 0.6013 0.236 0.000 0.000 0.000 0.764
#> GSM907812 1 0.6198 0.5301 0.480 0.000 0.008 0.108 0.404
#> GSM907815 1 0.7587 0.1872 0.428 0.000 0.056 0.284 0.232
#> GSM907817 5 0.0771 0.8723 0.004 0.020 0.000 0.000 0.976
#> GSM907821 5 0.0880 0.8648 0.000 0.032 0.000 0.000 0.968
#> GSM907824 5 0.0880 0.8648 0.000 0.032 0.000 0.000 0.968
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0767 0.8737 0.000 0.000 0.976 0.012 0.008 0.004
#> GSM907859 4 0.1686 0.8483 0.000 0.004 0.052 0.932 0.004 0.008
#> GSM907860 3 0.0458 0.8740 0.000 0.000 0.984 0.016 0.000 0.000
#> GSM907854 3 0.0622 0.8719 0.000 0.012 0.980 0.000 0.008 0.000
#> GSM907855 3 0.0767 0.8735 0.000 0.000 0.976 0.012 0.008 0.004
#> GSM907856 3 0.0767 0.8735 0.000 0.000 0.976 0.012 0.008 0.004
#> GSM907857 3 0.3486 0.6754 0.000 0.000 0.788 0.008 0.024 0.180
#> GSM907825 2 0.4111 0.8011 0.000 0.736 0.008 0.000 0.048 0.208
#> GSM907828 2 0.2762 0.8245 0.000 0.876 0.004 0.040 0.008 0.072
#> GSM907832 2 0.1777 0.8253 0.000 0.932 0.000 0.032 0.012 0.024
#> GSM907833 2 0.1777 0.8253 0.000 0.932 0.000 0.032 0.012 0.024
#> GSM907834 2 0.3992 0.8075 0.000 0.756 0.008 0.000 0.052 0.184
#> GSM907826 2 0.3633 0.8112 0.000 0.732 0.012 0.000 0.004 0.252
#> GSM907827 2 0.3626 0.8268 0.000 0.784 0.012 0.000 0.028 0.176
#> GSM907829 2 0.2164 0.8197 0.000 0.900 0.000 0.000 0.032 0.068
#> GSM907830 4 0.1985 0.8456 0.000 0.064 0.004 0.916 0.008 0.008
#> GSM907831 2 0.4158 0.7959 0.000 0.724 0.008 0.000 0.044 0.224
#> GSM907792 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.2473 0.9055 0.104 0.012 0.000 0.000 0.876 0.008
#> GSM907804 5 0.3998 0.8935 0.136 0.000 0.004 0.024 0.788 0.048
#> GSM907805 1 0.2448 0.7358 0.884 0.000 0.000 0.000 0.052 0.064
#> GSM907806 5 0.3371 0.8822 0.200 0.000 0.000 0.016 0.780 0.004
#> GSM907793 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.3087 0.8995 0.176 0.000 0.000 0.012 0.808 0.004
#> GSM907796 1 0.5496 0.4034 0.544 0.000 0.000 0.000 0.160 0.296
#> GSM907797 1 0.5753 0.1827 0.444 0.000 0.000 0.000 0.172 0.384
#> GSM907798 1 0.5496 0.4034 0.544 0.000 0.000 0.000 0.160 0.296
#> GSM907799 1 0.1390 0.7817 0.948 0.000 0.000 0.016 0.032 0.004
#> GSM907800 5 0.2053 0.9132 0.108 0.004 0.000 0.000 0.888 0.000
#> GSM907803 1 0.4313 0.0914 0.604 0.000 0.000 0.020 0.372 0.004
#> GSM907864 4 0.0806 0.8792 0.000 0.008 0.020 0.972 0.000 0.000
#> GSM907865 4 0.1994 0.8437 0.000 0.004 0.052 0.920 0.008 0.016
#> GSM907868 3 0.0508 0.8744 0.000 0.000 0.984 0.012 0.004 0.000
#> GSM907869 3 0.5768 0.0432 0.000 0.000 0.508 0.080 0.036 0.376
#> GSM907870 2 0.6253 0.5765 0.000 0.576 0.216 0.040 0.012 0.156
#> GSM907861 3 0.0508 0.8700 0.000 0.012 0.984 0.000 0.004 0.000
#> GSM907862 3 0.0767 0.8659 0.000 0.004 0.976 0.008 0.000 0.012
#> GSM907863 3 0.0767 0.8659 0.000 0.004 0.976 0.008 0.000 0.012
#> GSM907866 3 0.4732 0.3675 0.000 0.000 0.620 0.016 0.036 0.328
#> GSM907867 3 0.0260 0.8724 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907839 4 0.1010 0.8808 0.000 0.036 0.000 0.960 0.000 0.004
#> GSM907840 4 0.0922 0.8846 0.000 0.024 0.004 0.968 0.000 0.004
#> GSM907842 4 0.1010 0.8808 0.000 0.036 0.000 0.960 0.000 0.004
#> GSM907843 2 0.2706 0.8235 0.000 0.880 0.004 0.040 0.008 0.068
#> GSM907845 2 0.2239 0.8214 0.000 0.908 0.000 0.020 0.024 0.048
#> GSM907846 2 0.3141 0.7822 0.000 0.852 0.004 0.068 0.008 0.068
#> GSM907848 2 0.1777 0.8253 0.000 0.932 0.000 0.032 0.012 0.024
#> GSM907851 2 0.2871 0.8203 0.000 0.868 0.004 0.040 0.008 0.080
#> GSM907835 2 0.3564 0.8140 0.000 0.772 0.008 0.000 0.020 0.200
#> GSM907836 2 0.3584 0.8128 0.000 0.740 0.012 0.000 0.004 0.244
#> GSM907837 2 0.4107 0.7999 0.000 0.708 0.012 0.000 0.024 0.256
#> GSM907838 2 0.4167 0.8014 0.000 0.708 0.012 0.004 0.020 0.256
#> GSM907841 6 0.7476 0.1478 0.000 0.036 0.288 0.280 0.044 0.352
#> GSM907844 2 0.4227 0.8025 0.000 0.724 0.012 0.000 0.044 0.220
#> GSM907847 2 0.1478 0.8276 0.000 0.944 0.000 0.032 0.004 0.020
#> GSM907849 2 0.2635 0.8249 0.000 0.884 0.004 0.036 0.008 0.068
#> GSM907850 2 0.2451 0.8352 0.000 0.892 0.004 0.016 0.012 0.076
#> GSM907852 2 0.4061 0.8031 0.000 0.716 0.012 0.000 0.024 0.248
#> GSM907853 2 0.1458 0.8318 0.000 0.948 0.000 0.016 0.016 0.020
#> GSM907807 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.3437 0.5618 0.236 0.000 0.000 0.752 0.008 0.004
#> GSM907814 1 0.4344 0.1182 0.568 0.000 0.000 0.412 0.008 0.012
#> GSM907816 1 0.0622 0.7965 0.980 0.000 0.000 0.008 0.012 0.000
#> GSM907818 5 0.3550 0.8834 0.188 0.000 0.000 0.008 0.780 0.024
#> GSM907819 5 0.4359 0.8785 0.168 0.000 0.004 0.016 0.748 0.064
#> GSM907820 5 0.2473 0.9055 0.104 0.012 0.000 0.000 0.876 0.008
#> GSM907822 1 0.0622 0.7965 0.980 0.000 0.000 0.008 0.012 0.000
#> GSM907823 1 0.0881 0.7931 0.972 0.000 0.000 0.008 0.012 0.008
#> GSM907808 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.8014 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0146 0.8007 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907811 5 0.4106 0.7280 0.312 0.000 0.000 0.020 0.664 0.004
#> GSM907812 1 0.5496 0.4034 0.544 0.000 0.000 0.000 0.160 0.296
#> GSM907815 6 0.5726 0.3170 0.188 0.000 0.020 0.044 0.092 0.656
#> GSM907817 5 0.2053 0.9132 0.108 0.004 0.000 0.000 0.888 0.000
#> GSM907821 5 0.2006 0.9113 0.104 0.004 0.000 0.000 0.892 0.000
#> GSM907824 5 0.2006 0.9113 0.104 0.004 0.000 0.000 0.892 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
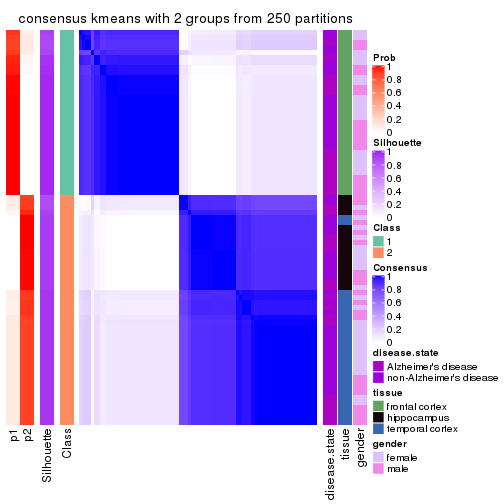
consensus_heatmap(res, k = 3)
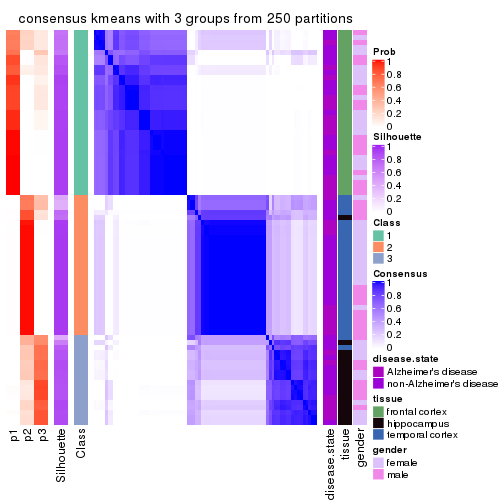
consensus_heatmap(res, k = 4)
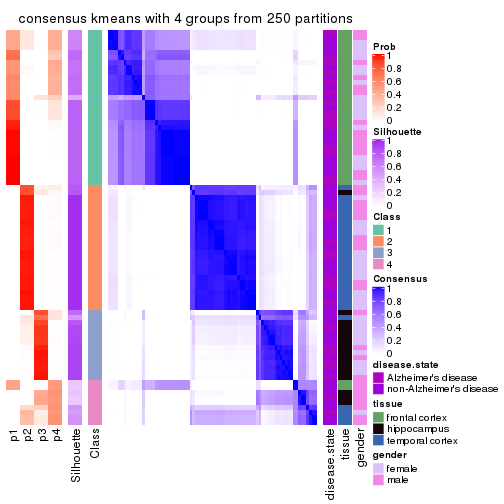
consensus_heatmap(res, k = 5)
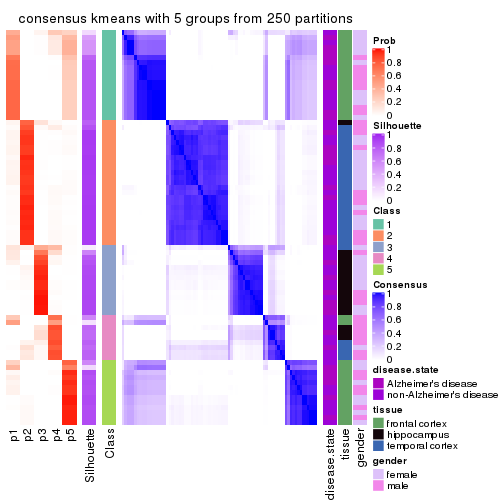
consensus_heatmap(res, k = 6)
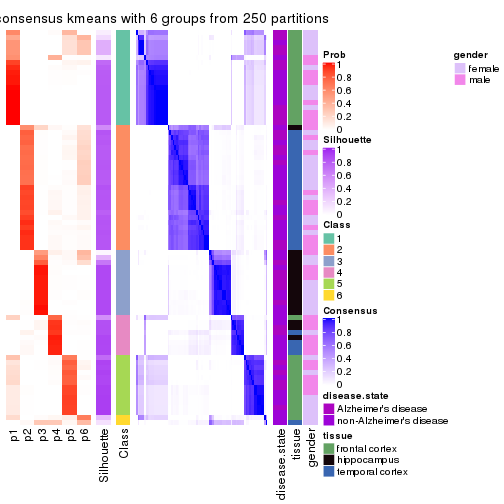
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
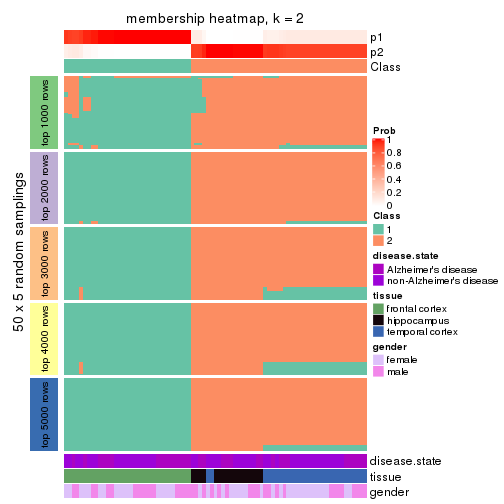
membership_heatmap(res, k = 3)
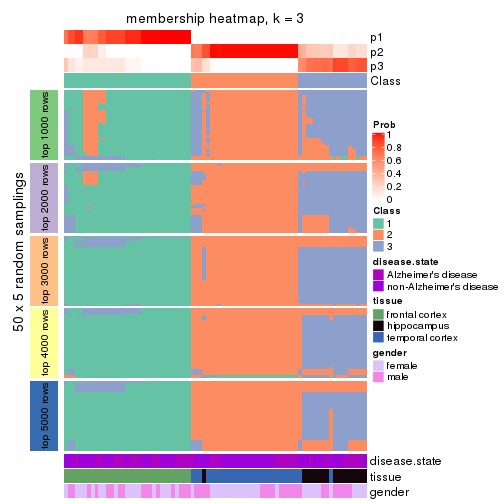
membership_heatmap(res, k = 4)
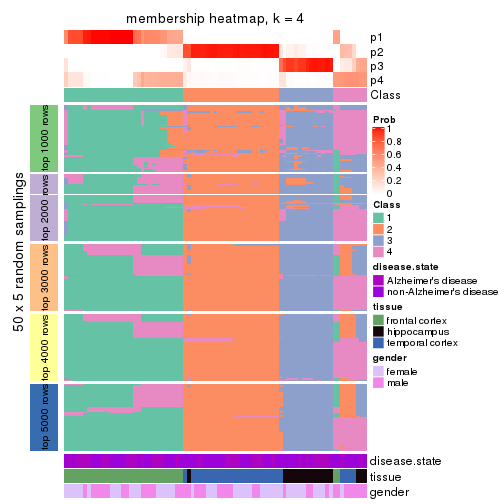
membership_heatmap(res, k = 5)
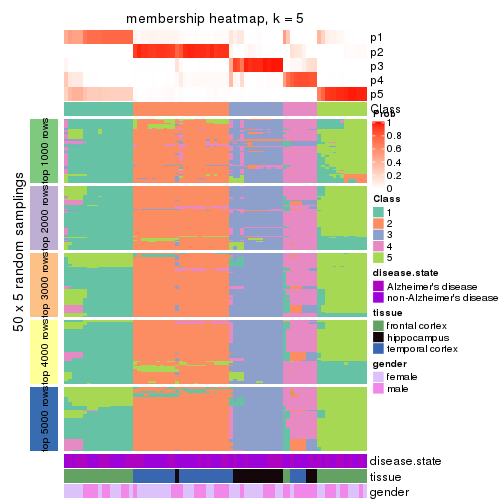
membership_heatmap(res, k = 6)
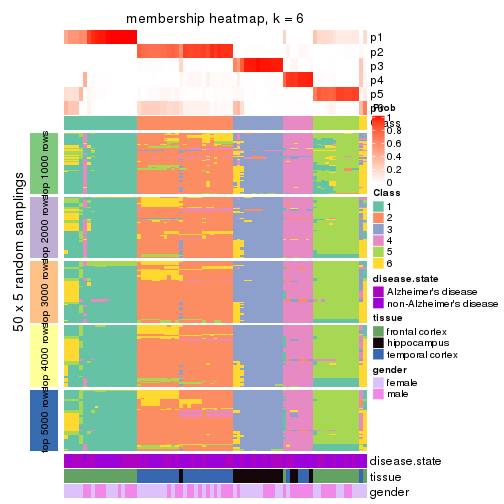
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
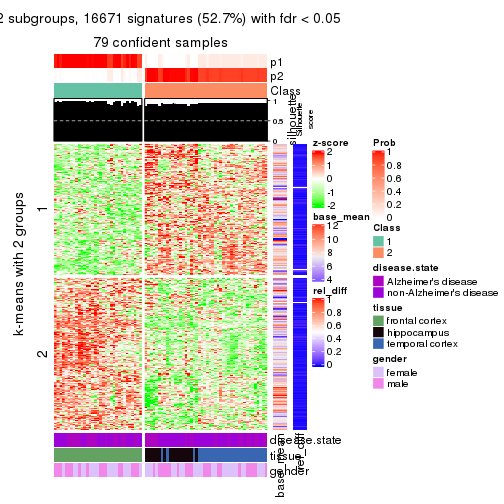
get_signatures(res, k = 3)
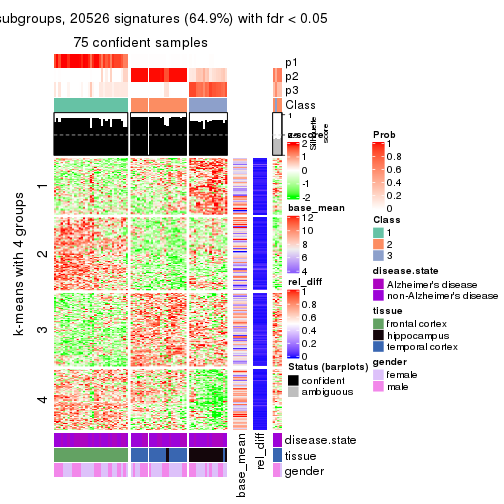
get_signatures(res, k = 4)
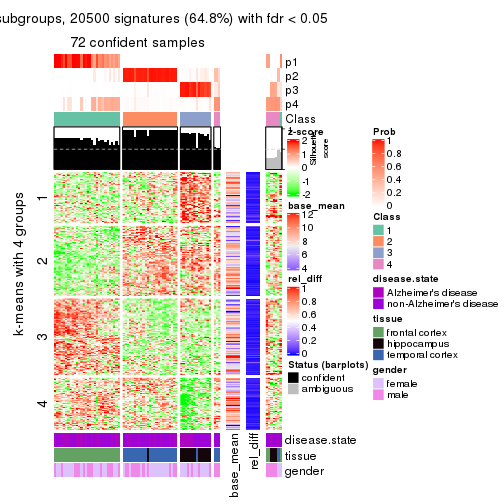
get_signatures(res, k = 5)
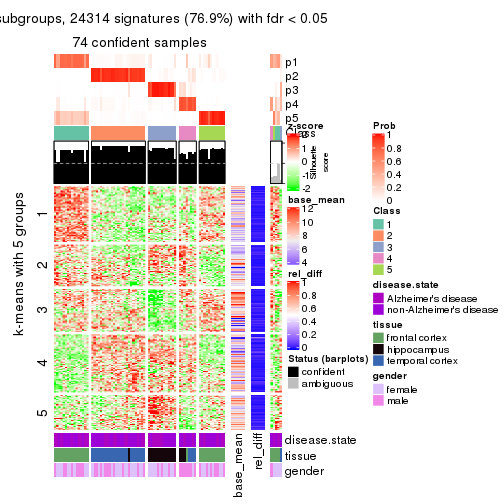
get_signatures(res, k = 6)
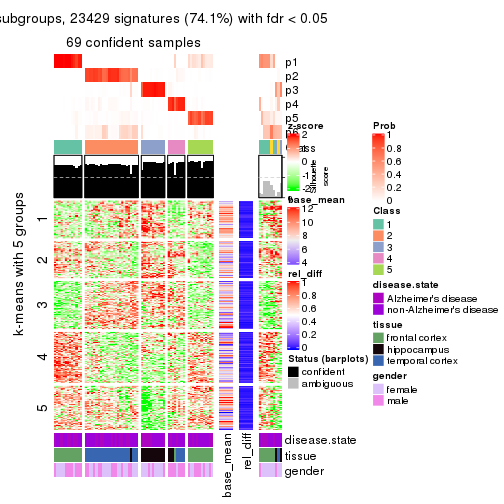
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
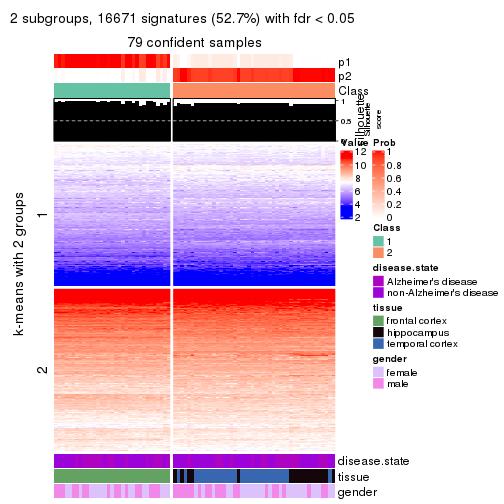
get_signatures(res, k = 3, scale_rows = FALSE)
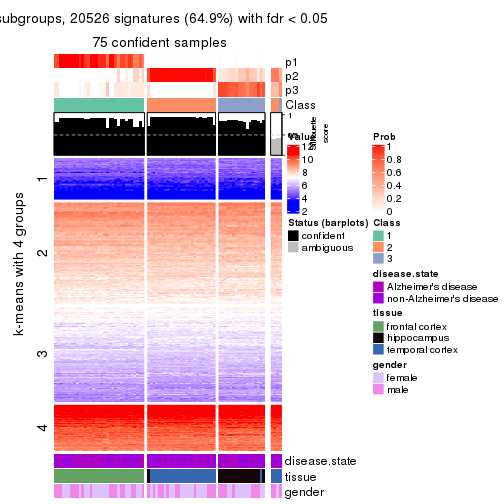
get_signatures(res, k = 4, scale_rows = FALSE)
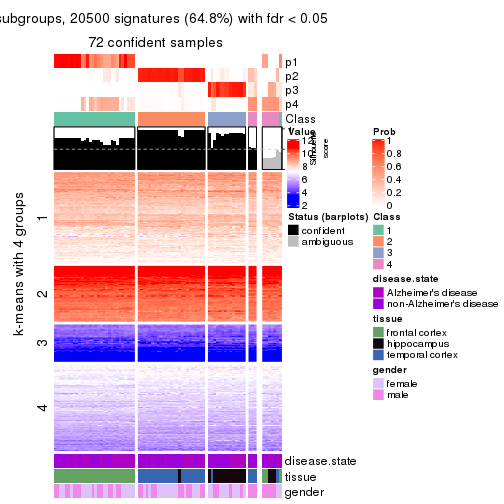
get_signatures(res, k = 5, scale_rows = FALSE)
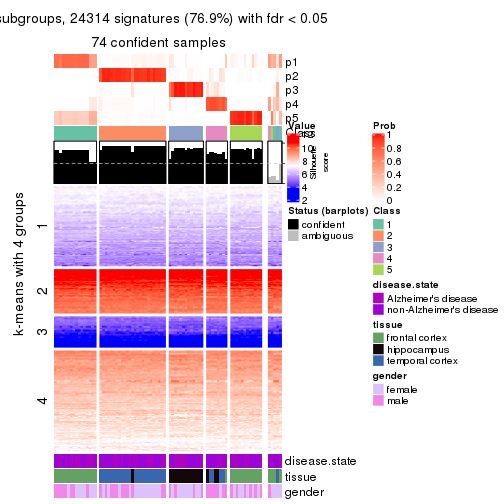
get_signatures(res, k = 6, scale_rows = FALSE)
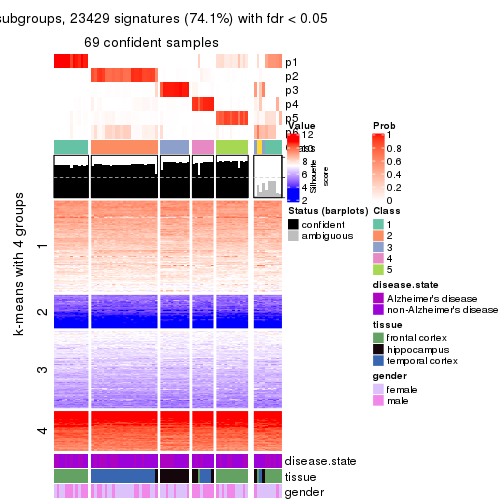
Compare the overlap of signatures from different k:
compare_signatures(res)
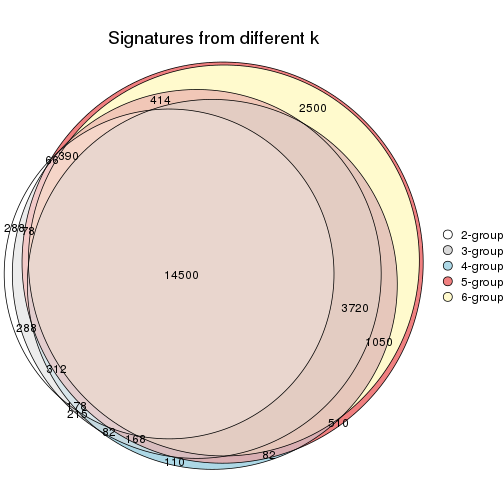
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
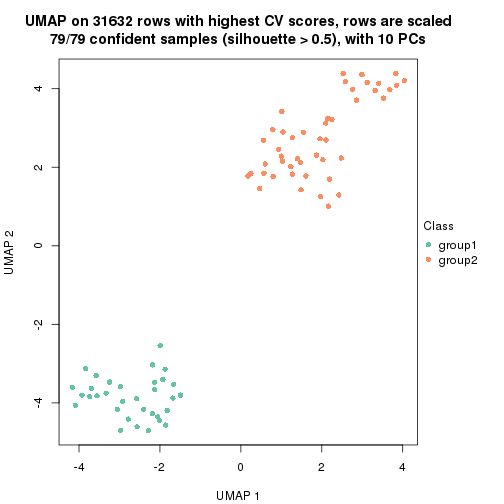
dimension_reduction(res, k = 3, method = "UMAP")
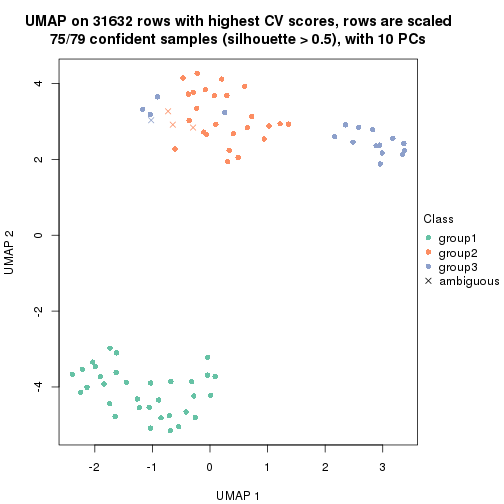
dimension_reduction(res, k = 4, method = "UMAP")
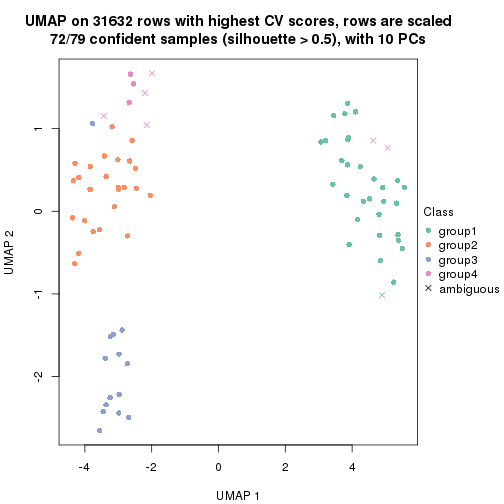
dimension_reduction(res, k = 5, method = "UMAP")
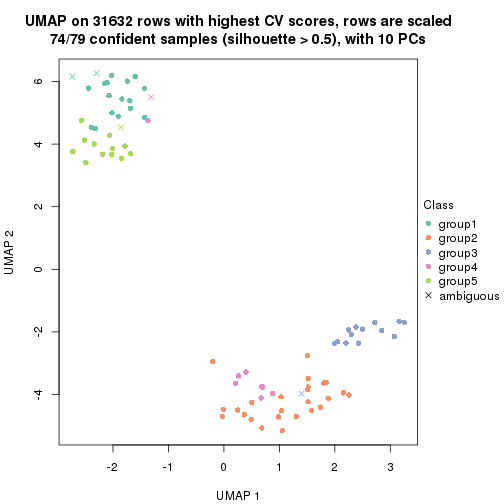
dimension_reduction(res, k = 6, method = "UMAP")
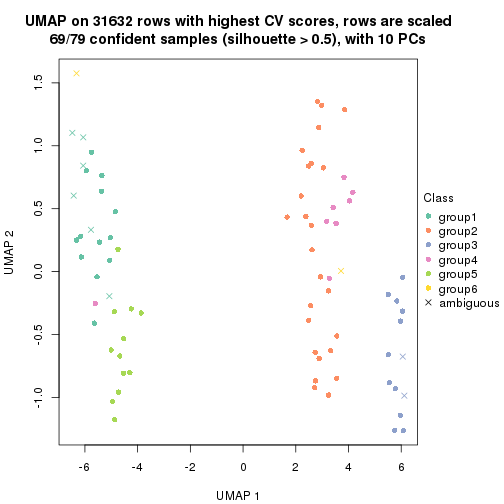
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
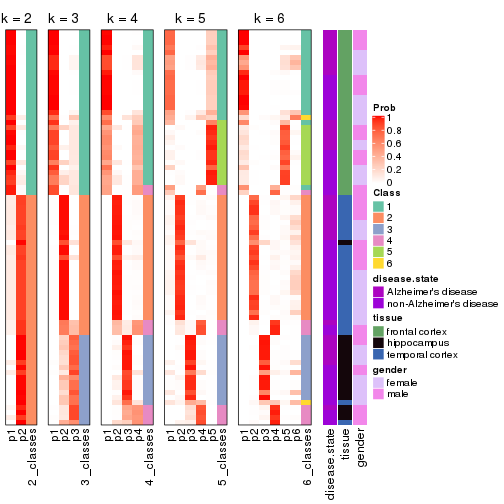
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:kmeans 79 0.599 7.00e-18 0.9838 2
#> CV:kmeans 75 0.769 2.12e-28 0.8743 3
#> CV:kmeans 72 0.342 1.69e-25 0.1550 4
#> CV:kmeans 74 0.775 2.30e-23 0.1506 5
#> CV:kmeans 69 0.720 3.03e-21 0.0987 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "skmeans"]
# you can also extract it by
# res = res_list["CV:skmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
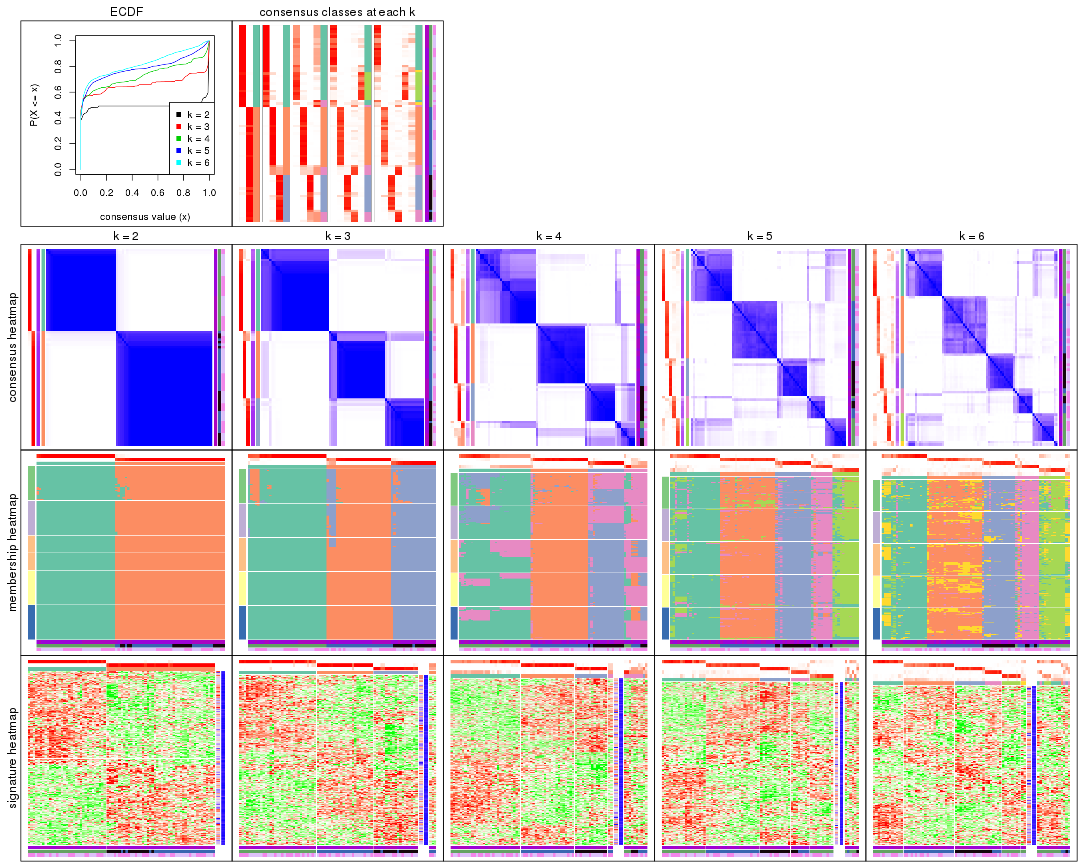
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
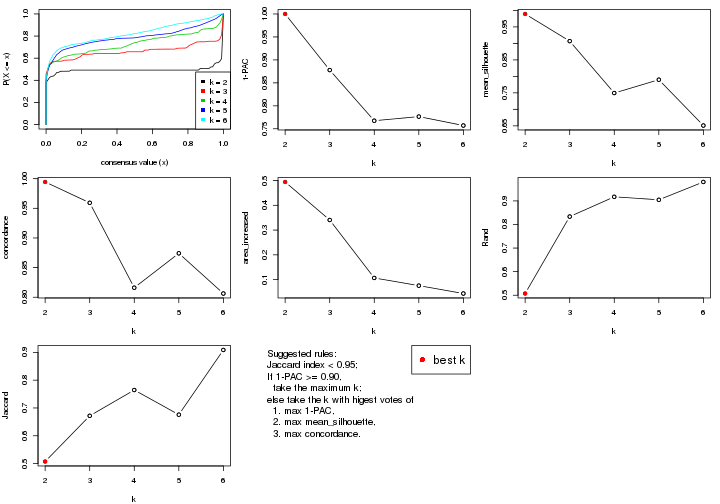
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.989 0.994 0.4942 0.507 0.507
#> 3 3 0.878 0.907 0.959 0.3406 0.833 0.672
#> 4 4 0.768 0.749 0.816 0.1066 0.917 0.765
#> 5 5 0.777 0.790 0.874 0.0756 0.905 0.676
#> 6 6 0.757 0.651 0.806 0.0437 0.980 0.909
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.992 0.000 1.000
#> GSM907859 2 0.0376 0.989 0.004 0.996
#> GSM907860 2 0.0000 0.992 0.000 1.000
#> GSM907854 2 0.0000 0.992 0.000 1.000
#> GSM907855 2 0.0000 0.992 0.000 1.000
#> GSM907856 2 0.0000 0.992 0.000 1.000
#> GSM907857 2 0.3879 0.924 0.076 0.924
#> GSM907825 2 0.0000 0.992 0.000 1.000
#> GSM907828 2 0.0000 0.992 0.000 1.000
#> GSM907832 2 0.0000 0.992 0.000 1.000
#> GSM907833 2 0.0000 0.992 0.000 1.000
#> GSM907834 2 0.0000 0.992 0.000 1.000
#> GSM907826 2 0.0000 0.992 0.000 1.000
#> GSM907827 2 0.0000 0.992 0.000 1.000
#> GSM907829 2 0.5737 0.853 0.136 0.864
#> GSM907830 2 0.0000 0.992 0.000 1.000
#> GSM907831 2 0.0000 0.992 0.000 1.000
#> GSM907792 1 0.0000 0.998 1.000 0.000
#> GSM907795 1 0.0000 0.998 1.000 0.000
#> GSM907801 1 0.0000 0.998 1.000 0.000
#> GSM907802 1 0.1414 0.980 0.980 0.020
#> GSM907804 1 0.0000 0.998 1.000 0.000
#> GSM907805 1 0.0000 0.998 1.000 0.000
#> GSM907806 1 0.0000 0.998 1.000 0.000
#> GSM907793 1 0.0000 0.998 1.000 0.000
#> GSM907794 1 0.0000 0.998 1.000 0.000
#> GSM907796 1 0.0000 0.998 1.000 0.000
#> GSM907797 1 0.0000 0.998 1.000 0.000
#> GSM907798 1 0.0000 0.998 1.000 0.000
#> GSM907799 1 0.0000 0.998 1.000 0.000
#> GSM907800 1 0.0000 0.998 1.000 0.000
#> GSM907803 1 0.0000 0.998 1.000 0.000
#> GSM907864 2 0.0000 0.992 0.000 1.000
#> GSM907865 2 0.1633 0.973 0.024 0.976
#> GSM907868 2 0.0000 0.992 0.000 1.000
#> GSM907869 2 0.3274 0.940 0.060 0.940
#> GSM907870 2 0.0000 0.992 0.000 1.000
#> GSM907861 2 0.0000 0.992 0.000 1.000
#> GSM907862 2 0.0000 0.992 0.000 1.000
#> GSM907863 2 0.0000 0.992 0.000 1.000
#> GSM907866 2 0.0000 0.992 0.000 1.000
#> GSM907867 2 0.0000 0.992 0.000 1.000
#> GSM907839 2 0.0000 0.992 0.000 1.000
#> GSM907840 2 0.0000 0.992 0.000 1.000
#> GSM907842 2 0.0000 0.992 0.000 1.000
#> GSM907843 2 0.0000 0.992 0.000 1.000
#> GSM907845 2 0.2948 0.948 0.052 0.948
#> GSM907846 2 0.0000 0.992 0.000 1.000
#> GSM907848 2 0.0000 0.992 0.000 1.000
#> GSM907851 2 0.0000 0.992 0.000 1.000
#> GSM907835 2 0.0000 0.992 0.000 1.000
#> GSM907836 2 0.0000 0.992 0.000 1.000
#> GSM907837 2 0.0000 0.992 0.000 1.000
#> GSM907838 2 0.0000 0.992 0.000 1.000
#> GSM907841 2 0.0000 0.992 0.000 1.000
#> GSM907844 2 0.0000 0.992 0.000 1.000
#> GSM907847 2 0.0000 0.992 0.000 1.000
#> GSM907849 2 0.1414 0.976 0.020 0.980
#> GSM907850 2 0.0000 0.992 0.000 1.000
#> GSM907852 2 0.0000 0.992 0.000 1.000
#> GSM907853 2 0.0000 0.992 0.000 1.000
#> GSM907807 1 0.0000 0.998 1.000 0.000
#> GSM907813 1 0.0000 0.998 1.000 0.000
#> GSM907814 1 0.0000 0.998 1.000 0.000
#> GSM907816 1 0.0000 0.998 1.000 0.000
#> GSM907818 1 0.0000 0.998 1.000 0.000
#> GSM907819 1 0.0000 0.998 1.000 0.000
#> GSM907820 1 0.2603 0.955 0.956 0.044
#> GSM907822 1 0.0000 0.998 1.000 0.000
#> GSM907823 1 0.0000 0.998 1.000 0.000
#> GSM907808 1 0.0000 0.998 1.000 0.000
#> GSM907809 1 0.0000 0.998 1.000 0.000
#> GSM907810 1 0.0000 0.998 1.000 0.000
#> GSM907811 1 0.0000 0.998 1.000 0.000
#> GSM907812 1 0.0000 0.998 1.000 0.000
#> GSM907815 1 0.0000 0.998 1.000 0.000
#> GSM907817 1 0.0000 0.998 1.000 0.000
#> GSM907821 1 0.0000 0.998 1.000 0.000
#> GSM907824 1 0.0376 0.994 0.996 0.004
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907859 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907860 3 0.0237 0.963 0.000 0.004 0.996
#> GSM907854 3 0.1529 0.941 0.000 0.040 0.960
#> GSM907855 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907856 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907857 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907825 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907828 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907832 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907834 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907826 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907827 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907829 2 0.0892 0.917 0.020 0.980 0.000
#> GSM907830 2 0.6204 0.318 0.000 0.576 0.424
#> GSM907831 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907792 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907802 1 0.4555 0.781 0.800 0.200 0.000
#> GSM907804 1 0.0424 0.963 0.992 0.000 0.008
#> GSM907805 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907797 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907798 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907800 1 0.0892 0.955 0.980 0.020 0.000
#> GSM907803 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907864 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907865 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907868 3 0.0424 0.962 0.000 0.008 0.992
#> GSM907869 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907870 3 0.4291 0.775 0.000 0.180 0.820
#> GSM907861 3 0.2878 0.885 0.000 0.096 0.904
#> GSM907862 3 0.0592 0.961 0.000 0.012 0.988
#> GSM907863 3 0.0592 0.961 0.000 0.012 0.988
#> GSM907866 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907867 3 0.1031 0.954 0.000 0.024 0.976
#> GSM907839 2 0.6267 0.241 0.000 0.548 0.452
#> GSM907840 3 0.4555 0.726 0.000 0.200 0.800
#> GSM907842 2 0.6267 0.241 0.000 0.548 0.452
#> GSM907843 2 0.0237 0.930 0.000 0.996 0.004
#> GSM907845 2 0.0424 0.927 0.008 0.992 0.000
#> GSM907846 2 0.5254 0.637 0.000 0.736 0.264
#> GSM907848 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907851 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907835 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907836 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907837 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907838 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907841 3 0.0000 0.964 0.000 0.000 1.000
#> GSM907844 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907849 2 0.0237 0.930 0.004 0.996 0.000
#> GSM907850 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907853 2 0.0000 0.933 0.000 1.000 0.000
#> GSM907807 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907813 1 0.0747 0.957 0.984 0.000 0.016
#> GSM907814 1 0.0592 0.960 0.988 0.000 0.012
#> GSM907816 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907820 1 0.4702 0.765 0.788 0.212 0.000
#> GSM907822 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.967 1.000 0.000 0.000
#> GSM907815 1 0.4002 0.811 0.840 0.000 0.160
#> GSM907817 1 0.1163 0.949 0.972 0.028 0.000
#> GSM907821 1 0.4121 0.819 0.832 0.168 0.000
#> GSM907824 1 0.4399 0.796 0.812 0.188 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0188 0.920 0.000 0.000 0.996 0.004
#> GSM907859 4 0.4985 0.303 0.000 0.000 0.468 0.532
#> GSM907860 3 0.0000 0.922 0.000 0.000 1.000 0.000
#> GSM907854 3 0.0779 0.908 0.000 0.016 0.980 0.004
#> GSM907855 3 0.0000 0.922 0.000 0.000 1.000 0.000
#> GSM907856 3 0.0000 0.922 0.000 0.000 1.000 0.000
#> GSM907857 3 0.0000 0.922 0.000 0.000 1.000 0.000
#> GSM907825 2 0.0779 0.950 0.016 0.980 0.000 0.004
#> GSM907828 2 0.0927 0.949 0.000 0.976 0.008 0.016
#> GSM907832 2 0.0779 0.950 0.016 0.980 0.000 0.004
#> GSM907833 2 0.0336 0.956 0.000 0.992 0.000 0.008
#> GSM907834 2 0.0524 0.954 0.008 0.988 0.000 0.004
#> GSM907826 2 0.0188 0.956 0.000 0.996 0.004 0.000
#> GSM907827 2 0.1209 0.938 0.000 0.964 0.032 0.004
#> GSM907829 2 0.3442 0.849 0.084 0.876 0.012 0.028
#> GSM907830 4 0.7289 0.487 0.000 0.268 0.200 0.532
#> GSM907831 2 0.0188 0.956 0.000 0.996 0.000 0.004
#> GSM907792 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907795 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907801 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907802 1 0.2714 0.572 0.884 0.112 0.000 0.004
#> GSM907804 1 0.2401 0.620 0.904 0.000 0.004 0.092
#> GSM907805 1 0.4961 0.768 0.552 0.000 0.000 0.448
#> GSM907806 1 0.2921 0.725 0.860 0.000 0.000 0.140
#> GSM907793 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907794 1 0.1211 0.692 0.960 0.000 0.000 0.040
#> GSM907796 1 0.4500 0.766 0.684 0.000 0.000 0.316
#> GSM907797 1 0.4585 0.764 0.668 0.000 0.000 0.332
#> GSM907798 1 0.4543 0.766 0.676 0.000 0.000 0.324
#> GSM907799 1 0.4948 0.771 0.560 0.000 0.000 0.440
#> GSM907800 1 0.1004 0.655 0.972 0.024 0.000 0.004
#> GSM907803 1 0.4331 0.758 0.712 0.000 0.000 0.288
#> GSM907864 4 0.4981 0.308 0.000 0.000 0.464 0.536
#> GSM907865 4 0.4981 0.308 0.000 0.000 0.464 0.536
#> GSM907868 3 0.0000 0.922 0.000 0.000 1.000 0.000
#> GSM907869 3 0.2868 0.752 0.000 0.000 0.864 0.136
#> GSM907870 3 0.3695 0.685 0.000 0.156 0.828 0.016
#> GSM907861 3 0.1302 0.879 0.000 0.044 0.956 0.000
#> GSM907862 3 0.0376 0.920 0.000 0.004 0.992 0.004
#> GSM907863 3 0.0188 0.921 0.000 0.000 0.996 0.004
#> GSM907866 3 0.0188 0.920 0.000 0.000 0.996 0.004
#> GSM907867 3 0.0592 0.913 0.000 0.016 0.984 0.000
#> GSM907839 4 0.7276 0.504 0.000 0.224 0.236 0.540
#> GSM907840 4 0.6607 0.428 0.000 0.088 0.376 0.536
#> GSM907842 4 0.7301 0.503 0.000 0.236 0.228 0.536
#> GSM907843 2 0.1109 0.943 0.000 0.968 0.004 0.028
#> GSM907845 2 0.1042 0.947 0.020 0.972 0.000 0.008
#> GSM907846 2 0.8102 -0.186 0.036 0.444 0.140 0.380
#> GSM907848 2 0.0376 0.955 0.004 0.992 0.000 0.004
#> GSM907851 2 0.0376 0.956 0.004 0.992 0.000 0.004
#> GSM907835 2 0.0000 0.957 0.000 1.000 0.000 0.000
#> GSM907836 2 0.0469 0.953 0.000 0.988 0.012 0.000
#> GSM907837 2 0.0000 0.957 0.000 1.000 0.000 0.000
#> GSM907838 2 0.0376 0.956 0.000 0.992 0.004 0.004
#> GSM907841 3 0.4454 0.347 0.000 0.000 0.692 0.308
#> GSM907844 2 0.0188 0.956 0.000 0.996 0.000 0.004
#> GSM907847 2 0.0188 0.956 0.000 0.996 0.000 0.004
#> GSM907849 2 0.1369 0.942 0.016 0.964 0.004 0.016
#> GSM907850 2 0.0000 0.957 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0000 0.957 0.000 1.000 0.000 0.000
#> GSM907853 2 0.0524 0.955 0.008 0.988 0.000 0.004
#> GSM907807 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907813 4 0.1004 0.310 0.024 0.000 0.004 0.972
#> GSM907814 4 0.1211 0.274 0.040 0.000 0.000 0.960
#> GSM907816 1 0.4967 0.769 0.548 0.000 0.000 0.452
#> GSM907818 1 0.0592 0.680 0.984 0.000 0.000 0.016
#> GSM907819 1 0.1792 0.701 0.932 0.000 0.000 0.068
#> GSM907820 1 0.2714 0.572 0.884 0.112 0.000 0.004
#> GSM907822 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907823 1 0.4955 0.770 0.556 0.000 0.000 0.444
#> GSM907808 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907809 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907810 1 0.4972 0.769 0.544 0.000 0.000 0.456
#> GSM907811 1 0.3266 0.724 0.832 0.000 0.000 0.168
#> GSM907812 1 0.4585 0.767 0.668 0.000 0.000 0.332
#> GSM907815 4 0.6508 -0.260 0.344 0.000 0.088 0.568
#> GSM907817 1 0.1004 0.655 0.972 0.024 0.000 0.004
#> GSM907821 1 0.1902 0.623 0.932 0.064 0.000 0.004
#> GSM907824 1 0.2125 0.612 0.920 0.076 0.000 0.004
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0566 0.892 0.000 0.000 0.984 0.012 0.004
#> GSM907859 4 0.3282 0.740 0.000 0.000 0.188 0.804 0.008
#> GSM907860 3 0.0566 0.893 0.000 0.000 0.984 0.012 0.004
#> GSM907854 3 0.0451 0.892 0.000 0.008 0.988 0.004 0.000
#> GSM907855 3 0.0404 0.893 0.000 0.000 0.988 0.012 0.000
#> GSM907856 3 0.0955 0.890 0.000 0.000 0.968 0.028 0.004
#> GSM907857 3 0.1012 0.887 0.000 0.000 0.968 0.020 0.012
#> GSM907825 2 0.1991 0.916 0.000 0.916 0.004 0.004 0.076
#> GSM907828 2 0.3569 0.850 0.000 0.816 0.004 0.152 0.028
#> GSM907832 2 0.2538 0.917 0.000 0.900 0.004 0.048 0.048
#> GSM907833 2 0.2446 0.918 0.000 0.900 0.000 0.056 0.044
#> GSM907834 2 0.1894 0.919 0.000 0.920 0.000 0.008 0.072
#> GSM907826 2 0.1087 0.925 0.000 0.968 0.008 0.008 0.016
#> GSM907827 2 0.2362 0.917 0.000 0.916 0.028 0.032 0.024
#> GSM907829 2 0.4955 0.786 0.044 0.792 0.048 0.052 0.064
#> GSM907830 4 0.2977 0.809 0.000 0.076 0.040 0.876 0.008
#> GSM907831 2 0.1662 0.922 0.000 0.936 0.004 0.004 0.056
#> GSM907792 1 0.0865 0.833 0.972 0.000 0.000 0.004 0.024
#> GSM907795 1 0.0000 0.833 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0865 0.832 0.972 0.000 0.000 0.004 0.024
#> GSM907802 5 0.1725 0.850 0.044 0.020 0.000 0.000 0.936
#> GSM907804 5 0.4121 0.791 0.112 0.000 0.000 0.100 0.788
#> GSM907805 1 0.2376 0.806 0.904 0.000 0.000 0.052 0.044
#> GSM907806 5 0.4403 0.472 0.384 0.000 0.000 0.008 0.608
#> GSM907793 1 0.0510 0.832 0.984 0.000 0.000 0.016 0.000
#> GSM907794 5 0.4422 0.627 0.300 0.000 0.004 0.016 0.680
#> GSM907796 1 0.4742 0.621 0.716 0.000 0.004 0.060 0.220
#> GSM907797 1 0.4735 0.654 0.728 0.000 0.004 0.072 0.196
#> GSM907798 1 0.4488 0.667 0.748 0.000 0.004 0.060 0.188
#> GSM907799 1 0.1792 0.810 0.916 0.000 0.000 0.000 0.084
#> GSM907800 5 0.1628 0.855 0.056 0.008 0.000 0.000 0.936
#> GSM907803 1 0.3607 0.589 0.752 0.000 0.000 0.004 0.244
#> GSM907864 4 0.2020 0.811 0.000 0.000 0.100 0.900 0.000
#> GSM907865 4 0.2719 0.782 0.000 0.000 0.144 0.852 0.004
#> GSM907868 3 0.0451 0.894 0.000 0.000 0.988 0.008 0.004
#> GSM907869 3 0.3878 0.641 0.000 0.000 0.748 0.236 0.016
#> GSM907870 3 0.6243 0.435 0.000 0.216 0.616 0.140 0.028
#> GSM907861 3 0.0771 0.885 0.000 0.020 0.976 0.004 0.000
#> GSM907862 3 0.1179 0.885 0.000 0.016 0.964 0.016 0.004
#> GSM907863 3 0.1173 0.884 0.000 0.012 0.964 0.020 0.004
#> GSM907866 3 0.1281 0.882 0.000 0.000 0.956 0.032 0.012
#> GSM907867 3 0.0486 0.893 0.000 0.004 0.988 0.004 0.004
#> GSM907839 4 0.2313 0.827 0.004 0.040 0.044 0.912 0.000
#> GSM907840 4 0.2270 0.825 0.000 0.020 0.076 0.904 0.000
#> GSM907842 4 0.2308 0.823 0.000 0.048 0.036 0.912 0.004
#> GSM907843 2 0.3759 0.817 0.000 0.792 0.004 0.180 0.024
#> GSM907845 2 0.2748 0.908 0.004 0.896 0.008 0.048 0.044
#> GSM907846 4 0.6342 0.544 0.000 0.252 0.080 0.608 0.060
#> GSM907848 2 0.2077 0.922 0.000 0.920 0.000 0.040 0.040
#> GSM907851 2 0.3478 0.888 0.016 0.852 0.004 0.096 0.032
#> GSM907835 2 0.1365 0.927 0.000 0.952 0.004 0.004 0.040
#> GSM907836 2 0.2277 0.922 0.000 0.920 0.028 0.024 0.028
#> GSM907837 2 0.2086 0.923 0.000 0.924 0.008 0.020 0.048
#> GSM907838 2 0.2217 0.922 0.000 0.920 0.012 0.024 0.044
#> GSM907841 3 0.4627 0.125 0.000 0.000 0.544 0.444 0.012
#> GSM907844 2 0.1605 0.925 0.000 0.944 0.004 0.012 0.040
#> GSM907847 2 0.1800 0.919 0.000 0.932 0.000 0.048 0.020
#> GSM907849 2 0.3765 0.879 0.012 0.832 0.004 0.108 0.044
#> GSM907850 2 0.1828 0.925 0.000 0.936 0.004 0.028 0.032
#> GSM907852 2 0.1864 0.923 0.000 0.924 0.004 0.004 0.068
#> GSM907853 2 0.1605 0.927 0.000 0.944 0.004 0.012 0.040
#> GSM907807 1 0.0000 0.833 1.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.4288 0.329 0.384 0.000 0.000 0.612 0.004
#> GSM907814 1 0.3333 0.647 0.788 0.000 0.000 0.208 0.004
#> GSM907816 1 0.1281 0.828 0.956 0.000 0.000 0.012 0.032
#> GSM907818 5 0.3224 0.801 0.160 0.000 0.000 0.016 0.824
#> GSM907819 5 0.5140 0.568 0.324 0.000 0.004 0.048 0.624
#> GSM907820 5 0.1648 0.846 0.040 0.020 0.000 0.000 0.940
#> GSM907822 1 0.0992 0.832 0.968 0.000 0.000 0.008 0.024
#> GSM907823 1 0.1082 0.831 0.964 0.000 0.000 0.008 0.028
#> GSM907808 1 0.0000 0.833 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0162 0.833 0.996 0.000 0.000 0.004 0.000
#> GSM907810 1 0.0451 0.834 0.988 0.000 0.000 0.004 0.008
#> GSM907811 1 0.4451 -0.196 0.504 0.000 0.000 0.004 0.492
#> GSM907812 1 0.4345 0.687 0.764 0.000 0.004 0.060 0.172
#> GSM907815 1 0.7199 0.434 0.548 0.000 0.088 0.212 0.152
#> GSM907817 5 0.1557 0.855 0.052 0.008 0.000 0.000 0.940
#> GSM907821 5 0.1960 0.854 0.048 0.020 0.000 0.004 0.928
#> GSM907824 5 0.1757 0.855 0.048 0.012 0.004 0.000 0.936
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.1434 0.8819 0.000 0.000 0.940 0.012 0.000 0.048
#> GSM907859 4 0.1563 0.7631 0.000 0.000 0.056 0.932 0.000 0.012
#> GSM907860 3 0.0964 0.8895 0.000 0.004 0.968 0.016 0.000 0.012
#> GSM907854 3 0.0837 0.8924 0.000 0.004 0.972 0.000 0.004 0.020
#> GSM907855 3 0.0862 0.8913 0.000 0.000 0.972 0.008 0.004 0.016
#> GSM907856 3 0.1624 0.8838 0.000 0.000 0.936 0.020 0.004 0.040
#> GSM907857 3 0.2402 0.8485 0.000 0.000 0.868 0.012 0.000 0.120
#> GSM907825 2 0.2537 0.8136 0.000 0.880 0.008 0.000 0.024 0.088
#> GSM907828 2 0.4653 0.7587 0.000 0.684 0.000 0.120 0.000 0.196
#> GSM907832 2 0.5225 0.7804 0.000 0.612 0.012 0.016 0.052 0.308
#> GSM907833 2 0.4928 0.7857 0.000 0.640 0.000 0.032 0.040 0.288
#> GSM907834 2 0.3854 0.8052 0.000 0.760 0.004 0.000 0.048 0.188
#> GSM907826 2 0.1514 0.8118 0.000 0.944 0.012 0.004 0.004 0.036
#> GSM907827 2 0.3996 0.7998 0.000 0.784 0.048 0.020 0.004 0.144
#> GSM907829 2 0.5987 0.4692 0.040 0.484 0.024 0.000 0.044 0.408
#> GSM907830 4 0.2000 0.7498 0.000 0.044 0.004 0.920 0.004 0.028
#> GSM907831 2 0.2718 0.8072 0.000 0.880 0.020 0.004 0.020 0.076
#> GSM907792 1 0.0717 0.7133 0.976 0.000 0.000 0.000 0.016 0.008
#> GSM907795 1 0.0146 0.7083 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907801 1 0.0603 0.7125 0.980 0.000 0.000 0.000 0.016 0.004
#> GSM907802 5 0.1452 0.7708 0.020 0.020 0.000 0.000 0.948 0.012
#> GSM907804 5 0.4882 0.6599 0.088 0.000 0.004 0.080 0.740 0.088
#> GSM907805 1 0.3979 0.2894 0.720 0.000 0.000 0.004 0.032 0.244
#> GSM907806 5 0.4921 0.3810 0.336 0.000 0.000 0.004 0.592 0.068
#> GSM907793 1 0.1812 0.6562 0.912 0.000 0.000 0.000 0.008 0.080
#> GSM907794 5 0.4747 0.3945 0.324 0.000 0.000 0.000 0.608 0.068
#> GSM907796 1 0.5772 -0.5304 0.472 0.000 0.000 0.004 0.156 0.368
#> GSM907797 6 0.5934 0.5122 0.396 0.000 0.000 0.016 0.136 0.452
#> GSM907798 1 0.5521 -0.5068 0.488 0.000 0.000 0.000 0.136 0.376
#> GSM907799 1 0.2619 0.6645 0.880 0.000 0.000 0.008 0.072 0.040
#> GSM907800 5 0.1546 0.7748 0.028 0.004 0.000 0.004 0.944 0.020
#> GSM907803 1 0.3364 0.5362 0.780 0.000 0.000 0.000 0.196 0.024
#> GSM907864 4 0.0865 0.7742 0.000 0.000 0.036 0.964 0.000 0.000
#> GSM907865 4 0.1297 0.7688 0.000 0.000 0.040 0.948 0.000 0.012
#> GSM907868 3 0.0858 0.8917 0.000 0.000 0.968 0.004 0.000 0.028
#> GSM907869 3 0.5107 0.5786 0.000 0.000 0.656 0.208 0.012 0.124
#> GSM907870 3 0.6432 0.3411 0.000 0.284 0.520 0.092 0.000 0.104
#> GSM907861 3 0.0912 0.8912 0.000 0.008 0.972 0.004 0.004 0.012
#> GSM907862 3 0.1542 0.8778 0.000 0.016 0.944 0.016 0.000 0.024
#> GSM907863 3 0.1149 0.8855 0.000 0.008 0.960 0.008 0.000 0.024
#> GSM907866 3 0.2933 0.8331 0.000 0.000 0.852 0.032 0.008 0.108
#> GSM907867 3 0.0976 0.8870 0.000 0.016 0.968 0.000 0.008 0.008
#> GSM907839 4 0.0862 0.7743 0.000 0.004 0.008 0.972 0.000 0.016
#> GSM907840 4 0.0260 0.7743 0.000 0.008 0.000 0.992 0.000 0.000
#> GSM907842 4 0.0717 0.7726 0.000 0.008 0.000 0.976 0.000 0.016
#> GSM907843 2 0.5365 0.7215 0.000 0.560 0.004 0.116 0.000 0.320
#> GSM907845 2 0.4529 0.7517 0.004 0.576 0.000 0.008 0.016 0.396
#> GSM907846 4 0.7821 0.2752 0.000 0.244 0.076 0.432 0.076 0.172
#> GSM907848 2 0.4330 0.7988 0.000 0.680 0.000 0.008 0.036 0.276
#> GSM907851 2 0.4784 0.7773 0.012 0.668 0.004 0.044 0.004 0.268
#> GSM907835 2 0.1900 0.8257 0.000 0.916 0.008 0.000 0.008 0.068
#> GSM907836 2 0.2630 0.8196 0.000 0.872 0.032 0.004 0.000 0.092
#> GSM907837 2 0.1994 0.8064 0.000 0.920 0.016 0.008 0.004 0.052
#> GSM907838 2 0.2698 0.7997 0.000 0.892 0.032 0.024 0.012 0.040
#> GSM907841 4 0.6207 0.0279 0.000 0.016 0.392 0.440 0.008 0.144
#> GSM907844 2 0.1950 0.8120 0.000 0.924 0.008 0.004 0.020 0.044
#> GSM907847 2 0.4253 0.7940 0.000 0.664 0.000 0.024 0.008 0.304
#> GSM907849 2 0.5563 0.7478 0.020 0.596 0.000 0.068 0.016 0.300
#> GSM907850 2 0.3510 0.8165 0.000 0.768 0.004 0.012 0.004 0.212
#> GSM907852 2 0.1624 0.8138 0.000 0.936 0.000 0.004 0.040 0.020
#> GSM907853 2 0.3915 0.8103 0.000 0.704 0.000 0.004 0.020 0.272
#> GSM907807 1 0.0000 0.7088 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.4118 0.2647 0.352 0.000 0.000 0.628 0.000 0.020
#> GSM907814 1 0.3608 0.3549 0.736 0.000 0.000 0.248 0.004 0.012
#> GSM907816 1 0.1700 0.6952 0.928 0.000 0.000 0.000 0.048 0.024
#> GSM907818 5 0.4548 0.6076 0.120 0.000 0.000 0.004 0.712 0.164
#> GSM907819 5 0.5946 0.1865 0.224 0.000 0.000 0.008 0.512 0.256
#> GSM907820 5 0.1630 0.7650 0.020 0.024 0.000 0.000 0.940 0.016
#> GSM907822 1 0.1341 0.7053 0.948 0.000 0.000 0.000 0.028 0.024
#> GSM907823 1 0.1713 0.6963 0.928 0.000 0.000 0.000 0.044 0.028
#> GSM907808 1 0.0508 0.7060 0.984 0.000 0.000 0.000 0.004 0.012
#> GSM907809 1 0.0935 0.6972 0.964 0.000 0.000 0.000 0.004 0.032
#> GSM907810 1 0.0508 0.7122 0.984 0.000 0.000 0.000 0.012 0.004
#> GSM907811 1 0.4381 0.0439 0.536 0.000 0.000 0.000 0.440 0.024
#> GSM907812 1 0.5443 -0.4750 0.504 0.000 0.000 0.004 0.108 0.384
#> GSM907815 6 0.7496 0.6139 0.248 0.000 0.052 0.140 0.088 0.472
#> GSM907817 5 0.1457 0.7750 0.028 0.004 0.000 0.004 0.948 0.016
#> GSM907821 5 0.1173 0.7729 0.016 0.008 0.000 0.000 0.960 0.016
#> GSM907824 5 0.1078 0.7729 0.016 0.008 0.000 0.000 0.964 0.012
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
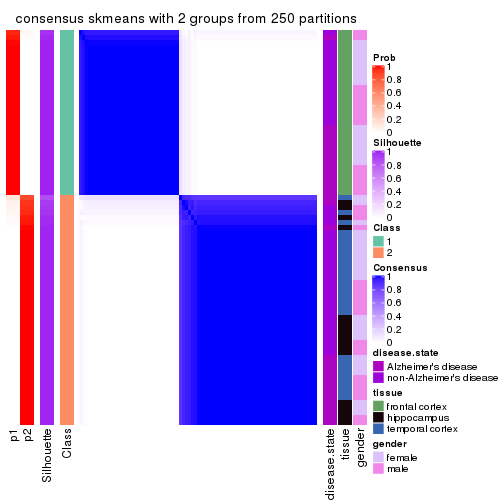
consensus_heatmap(res, k = 3)
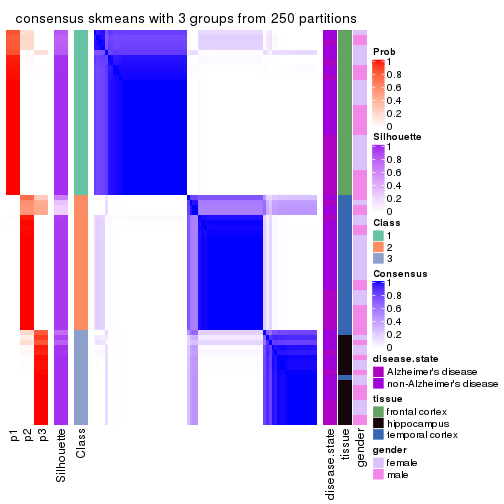
consensus_heatmap(res, k = 4)
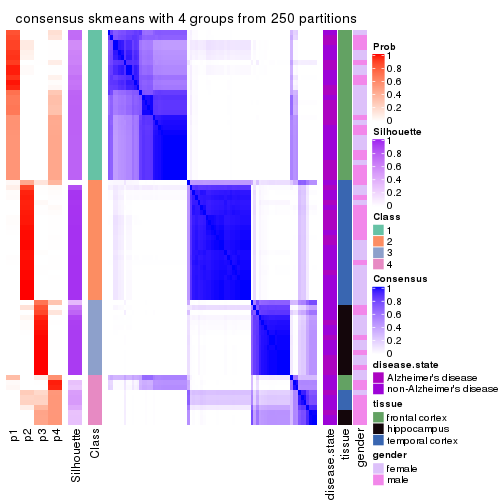
consensus_heatmap(res, k = 5)
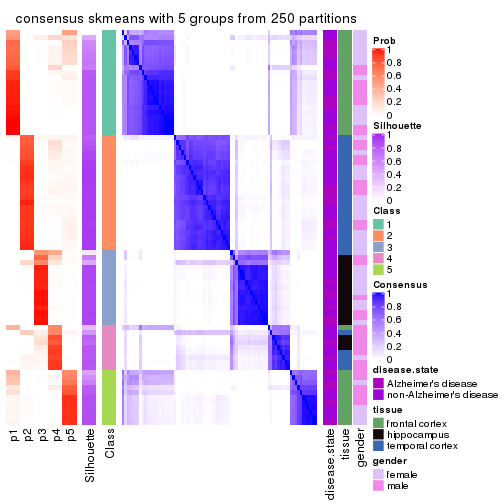
consensus_heatmap(res, k = 6)
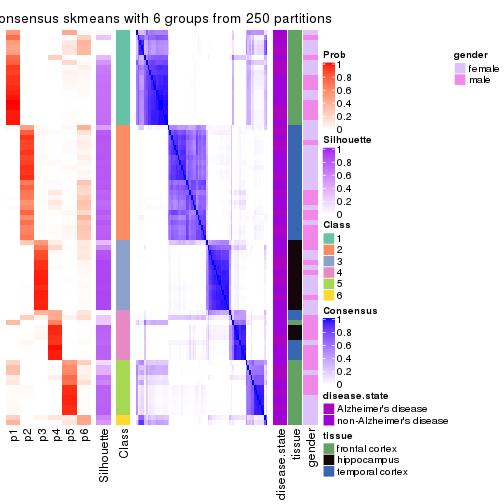
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
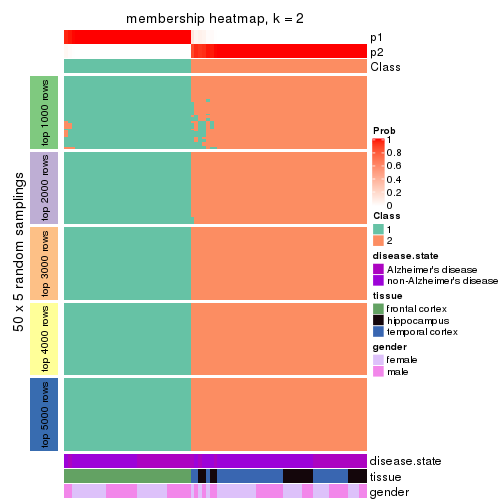
membership_heatmap(res, k = 3)
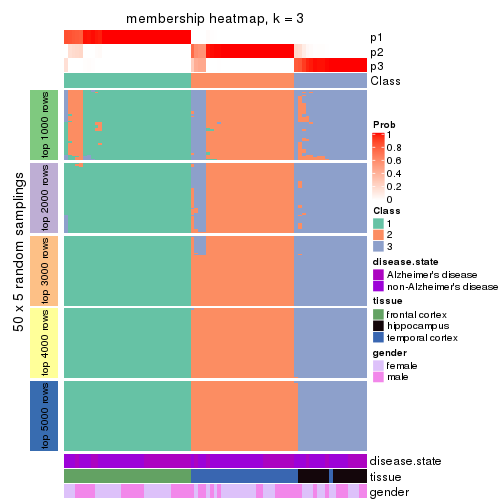
membership_heatmap(res, k = 4)
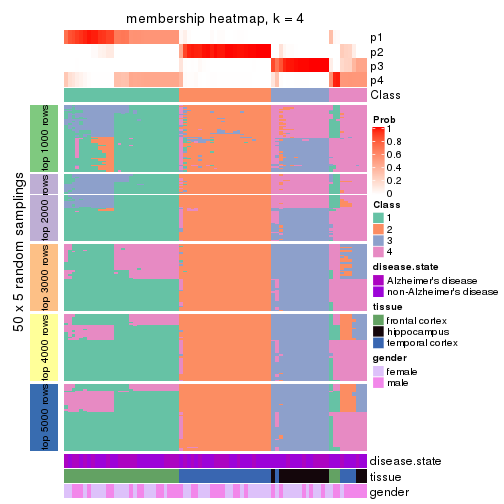
membership_heatmap(res, k = 5)
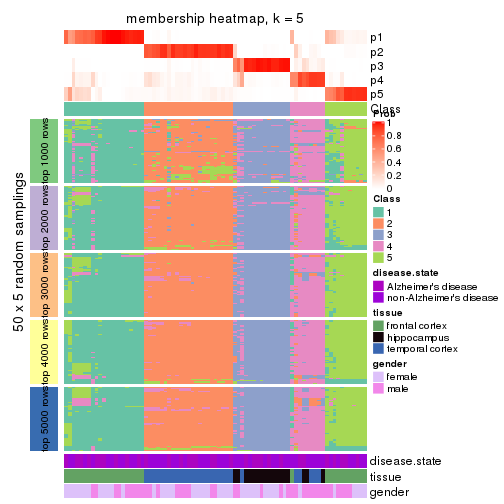
membership_heatmap(res, k = 6)
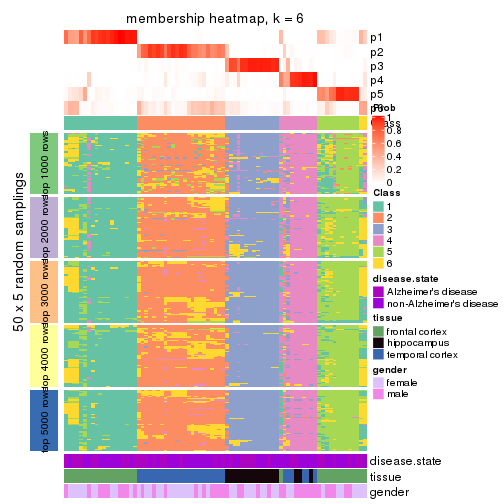
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
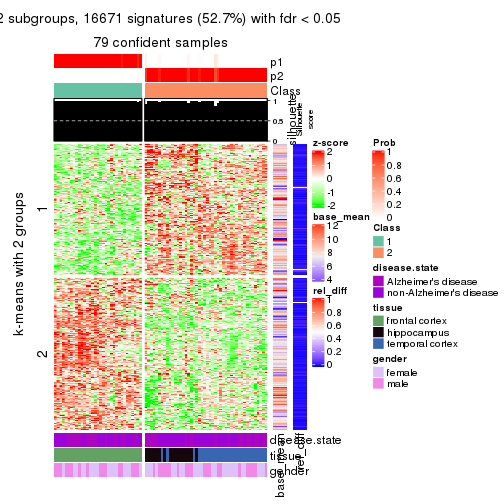
get_signatures(res, k = 3)
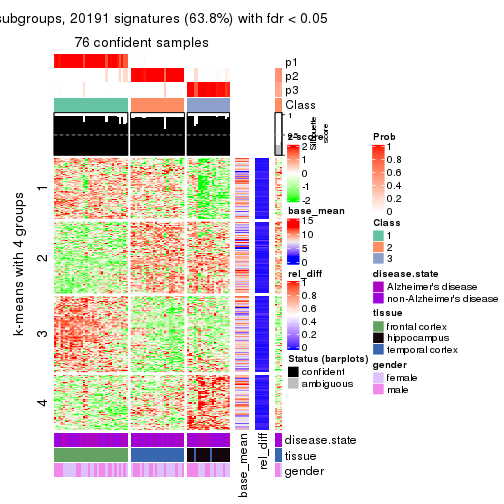
get_signatures(res, k = 4)
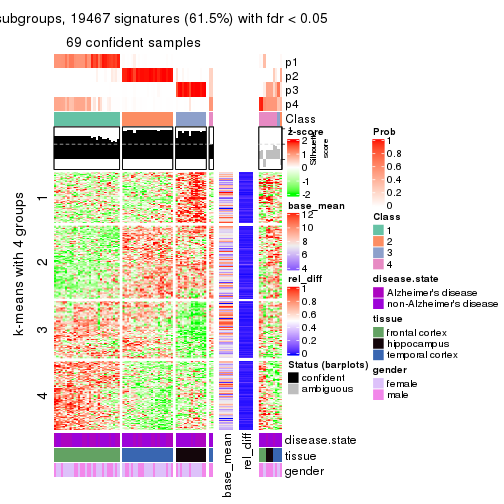
get_signatures(res, k = 5)
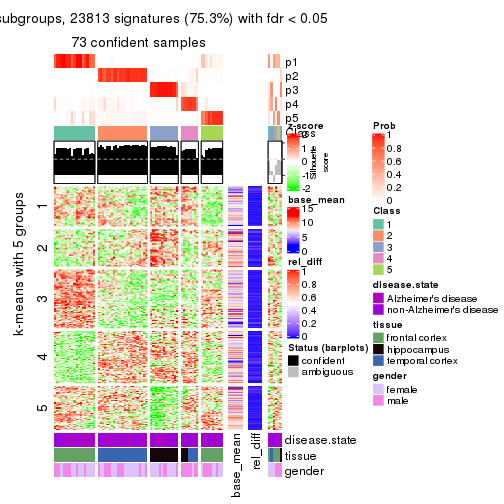
get_signatures(res, k = 6)
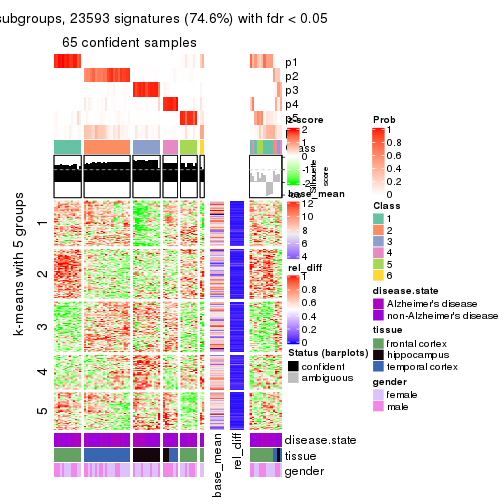
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
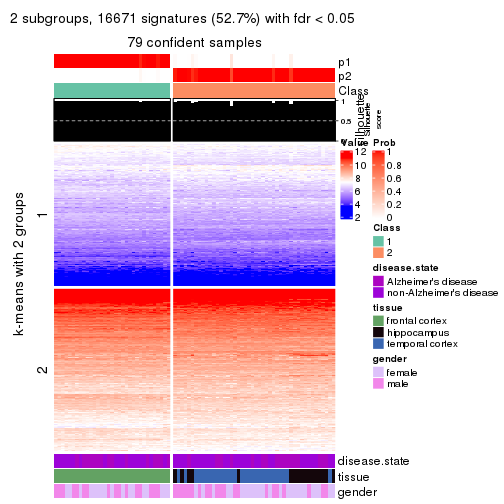
get_signatures(res, k = 3, scale_rows = FALSE)
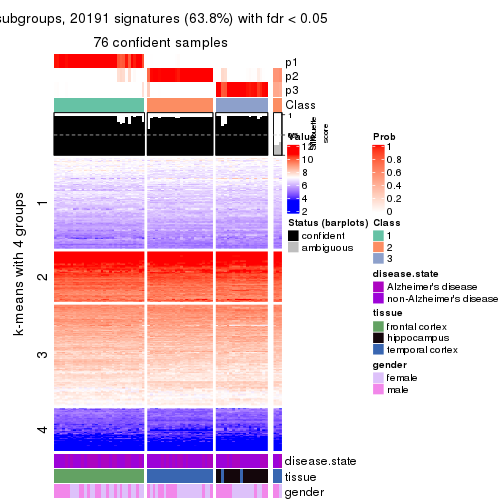
get_signatures(res, k = 4, scale_rows = FALSE)
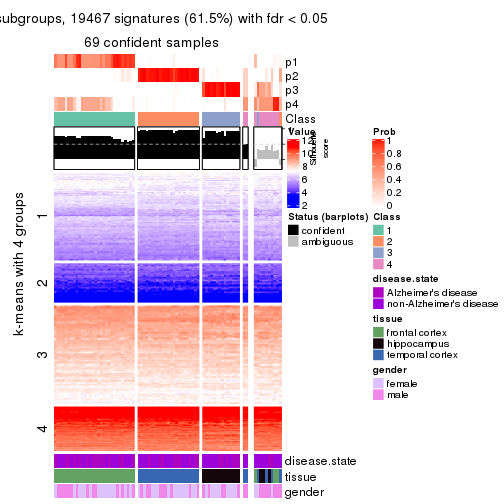
get_signatures(res, k = 5, scale_rows = FALSE)
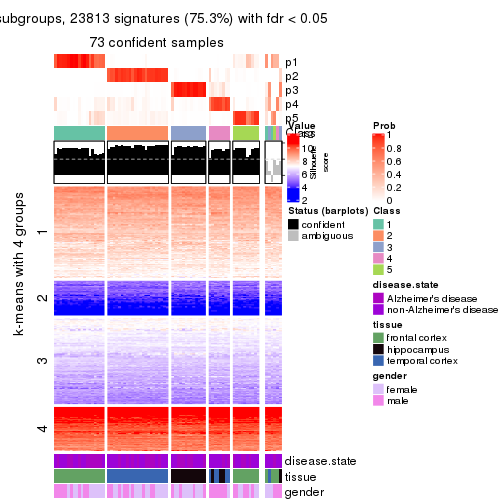
get_signatures(res, k = 6, scale_rows = FALSE)
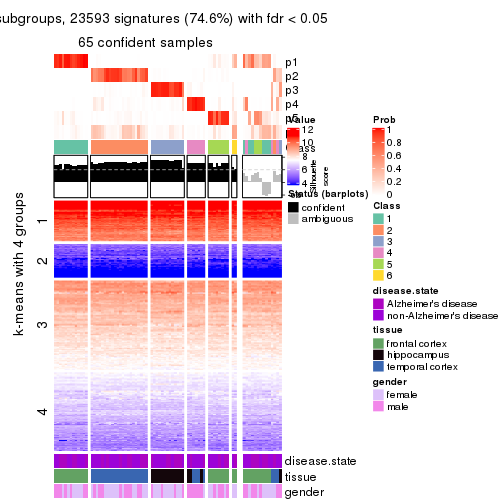
Compare the overlap of signatures from different k:
compare_signatures(res)
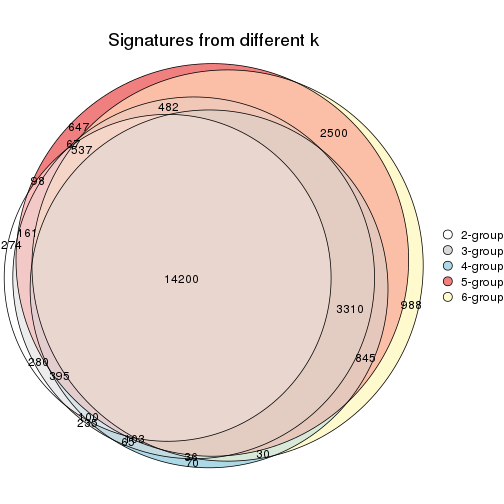
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
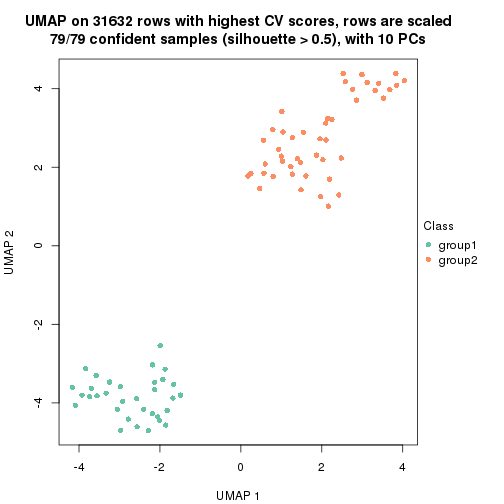
dimension_reduction(res, k = 3, method = "UMAP")
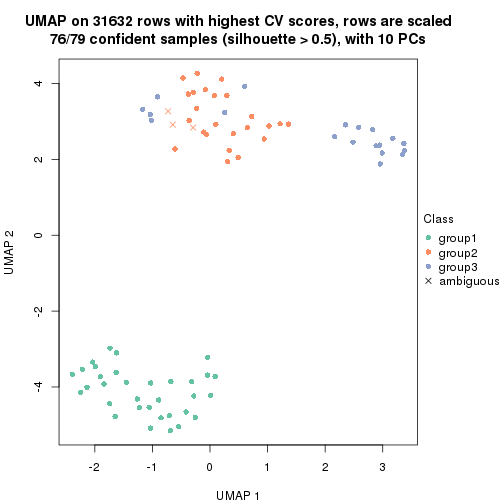
dimension_reduction(res, k = 4, method = "UMAP")
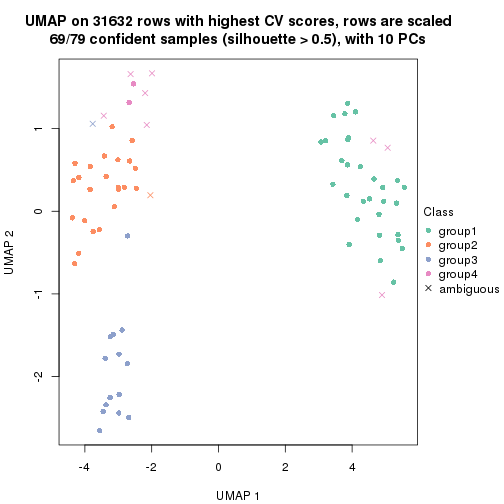
dimension_reduction(res, k = 5, method = "UMAP")
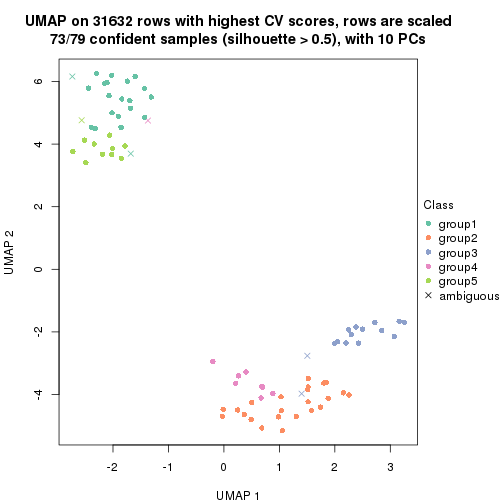
dimension_reduction(res, k = 6, method = "UMAP")
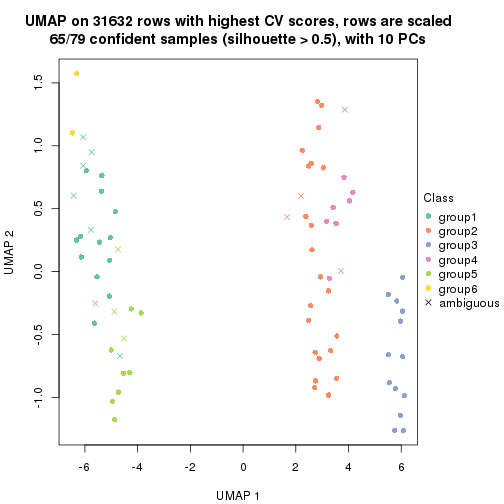
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
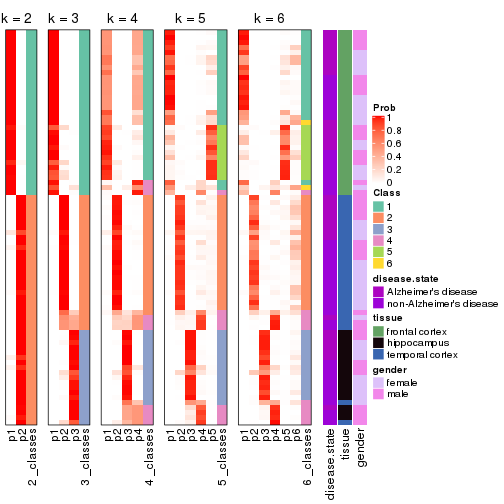
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:skmeans 79 0.599 7.00e-18 0.984 2
#> CV:skmeans 76 0.768 5.18e-29 0.870 3
#> CV:skmeans 69 0.525 2.65e-27 0.355 4
#> CV:skmeans 73 0.735 8.34e-25 0.123 5
#> CV:skmeans 65 0.961 9.07e-21 0.158 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "pam"]
# you can also extract it by
# res = res_list["CV:pam"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'pam' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
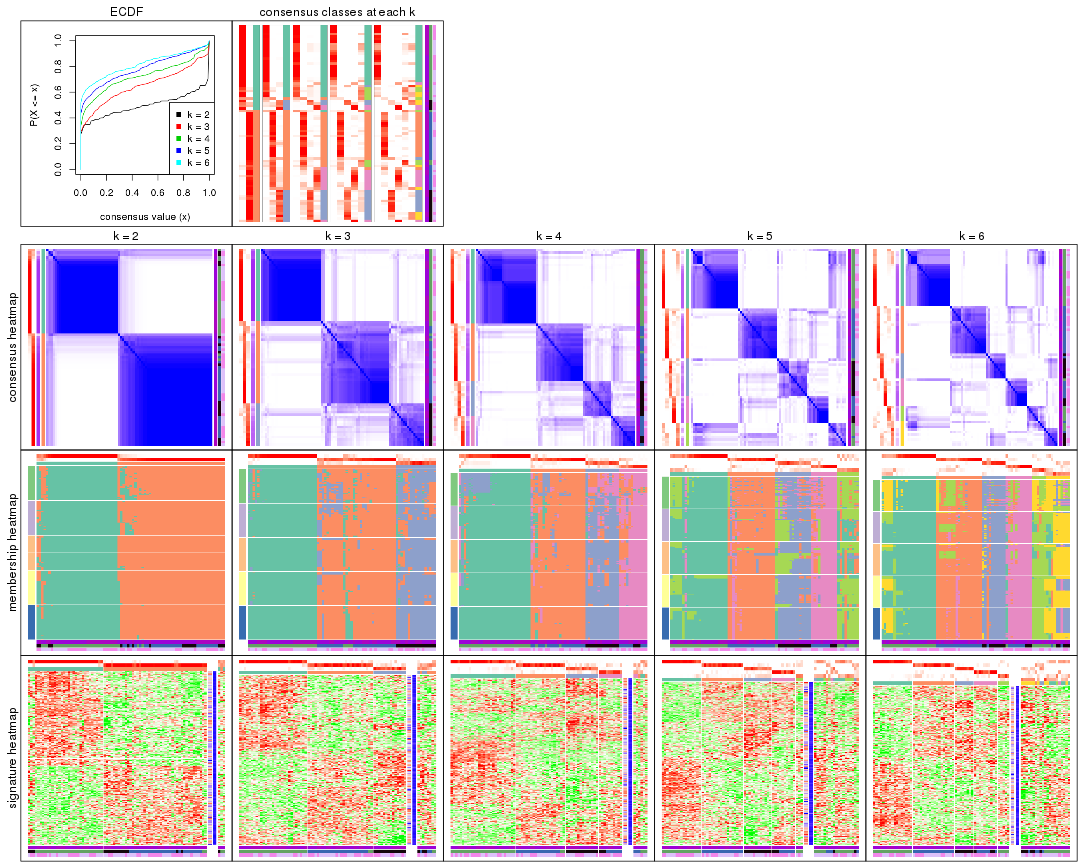
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
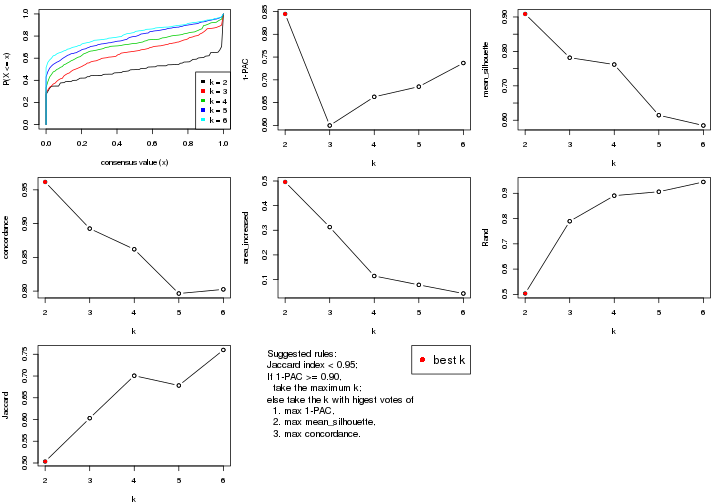
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.845 0.909 0.962 0.4961 0.503 0.503
#> 3 3 0.600 0.782 0.893 0.3130 0.789 0.603
#> 4 4 0.663 0.762 0.862 0.1144 0.891 0.701
#> 5 5 0.685 0.615 0.796 0.0784 0.906 0.678
#> 6 6 0.737 0.585 0.803 0.0432 0.945 0.760
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.963 0.000 1.000
#> GSM907859 1 0.9580 0.379 0.620 0.380
#> GSM907860 2 0.0376 0.961 0.004 0.996
#> GSM907854 2 0.0000 0.963 0.000 1.000
#> GSM907855 2 0.4022 0.903 0.080 0.920
#> GSM907856 2 0.0000 0.963 0.000 1.000
#> GSM907857 1 0.1184 0.940 0.984 0.016
#> GSM907825 2 0.0000 0.963 0.000 1.000
#> GSM907828 2 0.0000 0.963 0.000 1.000
#> GSM907832 2 0.0000 0.963 0.000 1.000
#> GSM907833 2 0.0000 0.963 0.000 1.000
#> GSM907834 2 0.0000 0.963 0.000 1.000
#> GSM907826 2 0.0000 0.963 0.000 1.000
#> GSM907827 2 0.0000 0.963 0.000 1.000
#> GSM907829 2 0.6887 0.786 0.184 0.816
#> GSM907830 2 0.0000 0.963 0.000 1.000
#> GSM907831 2 0.0000 0.963 0.000 1.000
#> GSM907792 1 0.0000 0.952 1.000 0.000
#> GSM907795 1 0.0000 0.952 1.000 0.000
#> GSM907801 1 0.0000 0.952 1.000 0.000
#> GSM907802 2 0.1184 0.954 0.016 0.984
#> GSM907804 1 0.0000 0.952 1.000 0.000
#> GSM907805 1 0.0000 0.952 1.000 0.000
#> GSM907806 1 0.0000 0.952 1.000 0.000
#> GSM907793 1 0.0000 0.952 1.000 0.000
#> GSM907794 1 0.0000 0.952 1.000 0.000
#> GSM907796 1 0.0000 0.952 1.000 0.000
#> GSM907797 1 0.0000 0.952 1.000 0.000
#> GSM907798 1 0.0000 0.952 1.000 0.000
#> GSM907799 1 0.0000 0.952 1.000 0.000
#> GSM907800 1 0.4022 0.884 0.920 0.080
#> GSM907803 1 0.0000 0.952 1.000 0.000
#> GSM907864 2 0.8081 0.682 0.248 0.752
#> GSM907865 1 0.0376 0.949 0.996 0.004
#> GSM907868 2 0.5946 0.836 0.144 0.856
#> GSM907869 1 0.9044 0.515 0.680 0.320
#> GSM907870 2 0.0000 0.963 0.000 1.000
#> GSM907861 2 0.0000 0.963 0.000 1.000
#> GSM907862 2 0.0000 0.963 0.000 1.000
#> GSM907863 2 0.0000 0.963 0.000 1.000
#> GSM907866 2 0.0000 0.963 0.000 1.000
#> GSM907867 2 0.0000 0.963 0.000 1.000
#> GSM907839 2 0.6623 0.796 0.172 0.828
#> GSM907840 2 0.1843 0.945 0.028 0.972
#> GSM907842 2 0.0376 0.961 0.004 0.996
#> GSM907843 2 0.0000 0.963 0.000 1.000
#> GSM907845 2 0.0000 0.963 0.000 1.000
#> GSM907846 2 0.0938 0.956 0.012 0.988
#> GSM907848 2 0.0000 0.963 0.000 1.000
#> GSM907851 2 0.4815 0.879 0.104 0.896
#> GSM907835 2 0.0000 0.963 0.000 1.000
#> GSM907836 2 0.0000 0.963 0.000 1.000
#> GSM907837 2 0.0000 0.963 0.000 1.000
#> GSM907838 2 0.0000 0.963 0.000 1.000
#> GSM907841 2 0.0000 0.963 0.000 1.000
#> GSM907844 2 0.0000 0.963 0.000 1.000
#> GSM907847 2 0.0000 0.963 0.000 1.000
#> GSM907849 2 0.4022 0.903 0.080 0.920
#> GSM907850 2 0.0000 0.963 0.000 1.000
#> GSM907852 2 0.0000 0.963 0.000 1.000
#> GSM907853 2 0.0000 0.963 0.000 1.000
#> GSM907807 1 0.0000 0.952 1.000 0.000
#> GSM907813 1 0.0000 0.952 1.000 0.000
#> GSM907814 1 0.0000 0.952 1.000 0.000
#> GSM907816 1 0.0000 0.952 1.000 0.000
#> GSM907818 1 0.0000 0.952 1.000 0.000
#> GSM907819 1 0.0000 0.952 1.000 0.000
#> GSM907820 2 0.1843 0.944 0.028 0.972
#> GSM907822 1 0.0000 0.952 1.000 0.000
#> GSM907823 1 0.0000 0.952 1.000 0.000
#> GSM907808 1 0.0000 0.952 1.000 0.000
#> GSM907809 1 0.0000 0.952 1.000 0.000
#> GSM907810 1 0.0000 0.952 1.000 0.000
#> GSM907811 1 0.0000 0.952 1.000 0.000
#> GSM907812 1 0.0000 0.952 1.000 0.000
#> GSM907815 1 0.0000 0.952 1.000 0.000
#> GSM907817 1 0.7674 0.710 0.776 0.224
#> GSM907821 2 0.9866 0.200 0.432 0.568
#> GSM907824 1 0.9970 0.133 0.532 0.468
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.5431 0.666 0.000 0.284 0.716
#> GSM907859 3 0.8505 0.463 0.144 0.256 0.600
#> GSM907860 3 0.1289 0.770 0.000 0.032 0.968
#> GSM907854 3 0.4750 0.728 0.000 0.216 0.784
#> GSM907855 3 0.1860 0.776 0.000 0.052 0.948
#> GSM907856 3 0.0000 0.762 0.000 0.000 1.000
#> GSM907857 3 0.5650 0.520 0.312 0.000 0.688
#> GSM907825 2 0.0237 0.810 0.000 0.996 0.004
#> GSM907828 2 0.3482 0.774 0.000 0.872 0.128
#> GSM907832 2 0.1643 0.805 0.000 0.956 0.044
#> GSM907833 2 0.1289 0.807 0.000 0.968 0.032
#> GSM907834 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907826 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907827 2 0.1411 0.807 0.000 0.964 0.036
#> GSM907829 2 0.5292 0.630 0.228 0.764 0.008
#> GSM907830 2 0.4346 0.740 0.000 0.816 0.184
#> GSM907831 2 0.1031 0.804 0.000 0.976 0.024
#> GSM907792 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907802 2 0.5138 0.566 0.252 0.748 0.000
#> GSM907804 1 0.0237 0.975 0.996 0.000 0.004
#> GSM907805 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907806 1 0.0237 0.975 0.996 0.004 0.000
#> GSM907793 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907797 1 0.0424 0.972 0.992 0.000 0.008
#> GSM907798 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907800 1 0.2796 0.882 0.908 0.092 0.000
#> GSM907803 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907864 3 0.3690 0.754 0.016 0.100 0.884
#> GSM907865 3 0.0592 0.763 0.012 0.000 0.988
#> GSM907868 3 0.3039 0.775 0.036 0.044 0.920
#> GSM907869 3 0.7199 0.614 0.108 0.180 0.712
#> GSM907870 3 0.6168 0.328 0.000 0.412 0.588
#> GSM907861 3 0.5560 0.660 0.000 0.300 0.700
#> GSM907862 3 0.3340 0.772 0.000 0.120 0.880
#> GSM907863 3 0.4346 0.749 0.000 0.184 0.816
#> GSM907866 3 0.5905 0.450 0.000 0.352 0.648
#> GSM907867 3 0.4654 0.737 0.000 0.208 0.792
#> GSM907839 2 0.6586 0.661 0.056 0.728 0.216
#> GSM907840 2 0.4842 0.695 0.000 0.776 0.224
#> GSM907842 2 0.4654 0.711 0.000 0.792 0.208
#> GSM907843 2 0.3551 0.770 0.000 0.868 0.132
#> GSM907845 2 0.1031 0.807 0.024 0.976 0.000
#> GSM907846 2 0.4121 0.744 0.000 0.832 0.168
#> GSM907848 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907851 2 0.3375 0.766 0.100 0.892 0.008
#> GSM907835 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907836 2 0.2959 0.749 0.000 0.900 0.100
#> GSM907837 2 0.5591 0.382 0.000 0.696 0.304
#> GSM907838 2 0.6204 0.198 0.000 0.576 0.424
#> GSM907841 2 0.6295 0.142 0.000 0.528 0.472
#> GSM907844 2 0.2959 0.742 0.000 0.900 0.100
#> GSM907847 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907849 2 0.4569 0.773 0.068 0.860 0.072
#> GSM907850 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907853 2 0.0000 0.809 0.000 1.000 0.000
#> GSM907807 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907813 1 0.3340 0.857 0.880 0.000 0.120
#> GSM907814 1 0.0892 0.961 0.980 0.000 0.020
#> GSM907816 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907820 2 0.3551 0.719 0.132 0.868 0.000
#> GSM907822 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.978 1.000 0.000 0.000
#> GSM907815 1 0.3038 0.879 0.896 0.000 0.104
#> GSM907817 1 0.4452 0.740 0.808 0.192 0.000
#> GSM907821 2 0.6126 0.343 0.400 0.600 0.000
#> GSM907824 2 0.6204 0.277 0.424 0.576 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.5035 0.692 0.000 0.196 0.748 0.056
#> GSM907859 4 0.1394 0.752 0.016 0.008 0.012 0.964
#> GSM907860 3 0.4098 0.705 0.000 0.012 0.784 0.204
#> GSM907854 3 0.2466 0.764 0.000 0.096 0.900 0.004
#> GSM907855 3 0.2919 0.760 0.000 0.044 0.896 0.060
#> GSM907856 3 0.2408 0.738 0.000 0.000 0.896 0.104
#> GSM907857 3 0.3731 0.617 0.120 0.000 0.844 0.036
#> GSM907825 2 0.1059 0.845 0.000 0.972 0.016 0.012
#> GSM907828 4 0.4011 0.706 0.000 0.208 0.008 0.784
#> GSM907832 2 0.2450 0.811 0.000 0.912 0.016 0.072
#> GSM907833 2 0.3443 0.733 0.000 0.848 0.016 0.136
#> GSM907834 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907826 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907827 2 0.1151 0.841 0.000 0.968 0.008 0.024
#> GSM907829 2 0.6719 0.576 0.168 0.680 0.116 0.036
#> GSM907830 4 0.3448 0.723 0.000 0.168 0.004 0.828
#> GSM907831 2 0.0895 0.847 0.000 0.976 0.020 0.004
#> GSM907792 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907802 2 0.4811 0.712 0.092 0.800 0.100 0.008
#> GSM907804 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907805 1 0.0336 0.915 0.992 0.000 0.008 0.000
#> GSM907806 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907794 1 0.3149 0.885 0.880 0.000 0.088 0.032
#> GSM907796 1 0.3149 0.885 0.880 0.000 0.088 0.032
#> GSM907797 1 0.3342 0.879 0.868 0.000 0.100 0.032
#> GSM907798 1 0.3149 0.885 0.880 0.000 0.088 0.032
#> GSM907799 1 0.2742 0.893 0.900 0.000 0.076 0.024
#> GSM907800 1 0.3966 0.870 0.852 0.020 0.096 0.032
#> GSM907803 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907864 4 0.1118 0.741 0.000 0.000 0.036 0.964
#> GSM907865 4 0.1256 0.744 0.008 0.000 0.028 0.964
#> GSM907868 3 0.1732 0.747 0.008 0.004 0.948 0.040
#> GSM907869 3 0.5562 0.564 0.008 0.024 0.652 0.316
#> GSM907870 3 0.7234 0.525 0.000 0.252 0.544 0.204
#> GSM907861 3 0.4564 0.594 0.000 0.328 0.672 0.000
#> GSM907862 3 0.6215 0.679 0.000 0.192 0.668 0.140
#> GSM907863 3 0.6251 0.681 0.000 0.196 0.664 0.140
#> GSM907866 3 0.5484 0.681 0.000 0.132 0.736 0.132
#> GSM907867 3 0.3074 0.753 0.000 0.152 0.848 0.000
#> GSM907839 4 0.1369 0.756 0.016 0.016 0.004 0.964
#> GSM907840 4 0.1209 0.761 0.000 0.032 0.004 0.964
#> GSM907842 4 0.1305 0.763 0.000 0.036 0.004 0.960
#> GSM907843 4 0.4814 0.627 0.000 0.316 0.008 0.676
#> GSM907845 2 0.3399 0.778 0.004 0.872 0.092 0.032
#> GSM907846 4 0.5130 0.581 0.000 0.332 0.016 0.652
#> GSM907848 2 0.0657 0.846 0.000 0.984 0.012 0.004
#> GSM907851 2 0.5771 0.559 0.080 0.704 0.004 0.212
#> GSM907835 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907836 2 0.2081 0.808 0.000 0.916 0.084 0.000
#> GSM907837 2 0.3552 0.742 0.000 0.848 0.128 0.024
#> GSM907838 2 0.7369 0.255 0.000 0.512 0.196 0.292
#> GSM907841 4 0.7304 0.405 0.000 0.208 0.260 0.532
#> GSM907844 2 0.2799 0.770 0.000 0.884 0.108 0.008
#> GSM907847 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907849 4 0.5602 0.308 0.020 0.472 0.000 0.508
#> GSM907850 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0000 0.848 0.000 1.000 0.000 0.000
#> GSM907853 2 0.0895 0.847 0.000 0.976 0.020 0.004
#> GSM907807 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907813 1 0.4933 0.308 0.568 0.000 0.000 0.432
#> GSM907814 1 0.0188 0.913 0.996 0.000 0.000 0.004
#> GSM907816 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907818 1 0.3149 0.885 0.880 0.000 0.088 0.032
#> GSM907819 1 0.2300 0.899 0.920 0.000 0.064 0.016
#> GSM907820 2 0.2486 0.824 0.028 0.920 0.048 0.004
#> GSM907822 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.916 1.000 0.000 0.000 0.000
#> GSM907811 1 0.1284 0.910 0.964 0.000 0.024 0.012
#> GSM907812 1 0.3149 0.885 0.880 0.000 0.088 0.032
#> GSM907815 1 0.5492 0.614 0.640 0.000 0.328 0.032
#> GSM907817 1 0.5607 0.792 0.768 0.092 0.104 0.036
#> GSM907821 1 0.7194 0.379 0.552 0.332 0.096 0.020
#> GSM907824 2 0.6694 0.317 0.360 0.568 0.040 0.032
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.3012 0.6354 0.000 0.060 0.876 0.056 0.008
#> GSM907859 4 0.0162 0.8246 0.000 0.000 0.004 0.996 0.000
#> GSM907860 3 0.5164 0.6880 0.000 0.000 0.672 0.096 0.232
#> GSM907854 3 0.3211 0.7241 0.000 0.008 0.824 0.004 0.164
#> GSM907855 3 0.3154 0.7206 0.000 0.004 0.836 0.012 0.148
#> GSM907856 3 0.0703 0.6819 0.000 0.000 0.976 0.024 0.000
#> GSM907857 3 0.3280 0.5787 0.004 0.000 0.808 0.004 0.184
#> GSM907825 2 0.1869 0.8393 0.000 0.936 0.016 0.012 0.036
#> GSM907828 4 0.3642 0.6769 0.000 0.232 0.008 0.760 0.000
#> GSM907832 2 0.3367 0.7953 0.000 0.856 0.016 0.088 0.040
#> GSM907833 2 0.3735 0.7647 0.000 0.828 0.016 0.116 0.040
#> GSM907834 2 0.0703 0.8485 0.000 0.976 0.000 0.000 0.024
#> GSM907826 2 0.0162 0.8486 0.000 0.996 0.004 0.000 0.000
#> GSM907827 2 0.1041 0.8433 0.000 0.964 0.004 0.032 0.000
#> GSM907829 5 0.6108 0.2433 0.108 0.432 0.004 0.000 0.456
#> GSM907830 4 0.2471 0.7699 0.000 0.136 0.000 0.864 0.000
#> GSM907831 2 0.1911 0.8388 0.000 0.932 0.028 0.004 0.036
#> GSM907792 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.4982 0.5153 0.036 0.244 0.016 0.004 0.700
#> GSM907804 1 0.3752 0.3984 0.708 0.000 0.000 0.000 0.292
#> GSM907805 1 0.0404 0.7876 0.988 0.000 0.000 0.000 0.012
#> GSM907806 1 0.0290 0.7887 0.992 0.000 0.000 0.000 0.008
#> GSM907793 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907794 1 0.4297 0.0219 0.528 0.000 0.000 0.000 0.472
#> GSM907796 1 0.4219 0.1554 0.584 0.000 0.000 0.000 0.416
#> GSM907797 5 0.4074 0.3773 0.364 0.000 0.000 0.000 0.636
#> GSM907798 1 0.4219 0.1554 0.584 0.000 0.000 0.000 0.416
#> GSM907799 1 0.3336 0.5879 0.772 0.000 0.000 0.000 0.228
#> GSM907800 5 0.4291 0.1237 0.464 0.000 0.000 0.000 0.536
#> GSM907803 1 0.1792 0.7294 0.916 0.000 0.000 0.000 0.084
#> GSM907864 4 0.0162 0.8246 0.000 0.000 0.004 0.996 0.000
#> GSM907865 4 0.0162 0.8246 0.000 0.000 0.004 0.996 0.000
#> GSM907868 3 0.3942 0.7170 0.000 0.000 0.728 0.012 0.260
#> GSM907869 3 0.3750 0.4909 0.000 0.000 0.756 0.232 0.012
#> GSM907870 3 0.7977 0.4781 0.000 0.272 0.424 0.120 0.184
#> GSM907861 3 0.6102 0.6387 0.000 0.200 0.568 0.000 0.232
#> GSM907862 3 0.6688 0.6673 0.000 0.096 0.592 0.080 0.232
#> GSM907863 3 0.6536 0.6707 0.000 0.124 0.596 0.048 0.232
#> GSM907866 3 0.3183 0.6085 0.000 0.028 0.856 0.108 0.008
#> GSM907867 3 0.4960 0.7112 0.000 0.080 0.688 0.000 0.232
#> GSM907839 4 0.0162 0.8246 0.000 0.000 0.004 0.996 0.000
#> GSM907840 4 0.0162 0.8246 0.000 0.000 0.004 0.996 0.000
#> GSM907842 4 0.0566 0.8220 0.000 0.012 0.004 0.984 0.000
#> GSM907843 4 0.4372 0.6863 0.000 0.200 0.008 0.752 0.040
#> GSM907845 2 0.3074 0.6424 0.000 0.804 0.000 0.000 0.196
#> GSM907846 4 0.5157 0.5220 0.000 0.288 0.016 0.656 0.040
#> GSM907848 2 0.1605 0.8405 0.000 0.944 0.012 0.004 0.040
#> GSM907851 2 0.5436 0.5237 0.084 0.672 0.008 0.232 0.004
#> GSM907835 2 0.0000 0.8484 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.1701 0.8246 0.000 0.936 0.048 0.000 0.016
#> GSM907837 2 0.2669 0.7628 0.000 0.876 0.020 0.000 0.104
#> GSM907838 2 0.8045 0.1295 0.000 0.440 0.148 0.200 0.212
#> GSM907841 4 0.5720 0.3199 0.000 0.020 0.416 0.520 0.044
#> GSM907844 2 0.0963 0.8400 0.000 0.964 0.036 0.000 0.000
#> GSM907847 2 0.1043 0.8452 0.000 0.960 0.000 0.000 0.040
#> GSM907849 2 0.5051 -0.1735 0.024 0.488 0.000 0.484 0.004
#> GSM907850 2 0.0000 0.8484 0.000 1.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.8484 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.0798 0.8482 0.000 0.976 0.016 0.000 0.008
#> GSM907807 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.4297 0.1236 0.528 0.000 0.000 0.472 0.000
#> GSM907814 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0703 0.7789 0.976 0.000 0.000 0.000 0.024
#> GSM907818 5 0.4287 0.0750 0.460 0.000 0.000 0.000 0.540
#> GSM907819 1 0.3876 0.3813 0.684 0.000 0.000 0.000 0.316
#> GSM907820 5 0.5407 0.0233 0.020 0.460 0.016 0.004 0.500
#> GSM907822 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.7929 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2471 0.6957 0.864 0.000 0.000 0.000 0.136
#> GSM907812 1 0.4219 0.1554 0.584 0.000 0.000 0.000 0.416
#> GSM907815 3 0.6715 -0.2629 0.248 0.000 0.392 0.000 0.360
#> GSM907817 5 0.4025 0.4605 0.292 0.008 0.000 0.000 0.700
#> GSM907821 5 0.5251 0.6013 0.092 0.180 0.012 0.004 0.712
#> GSM907824 5 0.5608 0.5771 0.172 0.188 0.000 0.000 0.640
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 6 0.5845 0.2969 0.000 0.000 0.296 0.068 0.068 0.568
#> GSM907859 4 0.0000 0.8031 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907860 3 0.0865 0.7709 0.000 0.000 0.964 0.036 0.000 0.000
#> GSM907854 3 0.2593 0.6362 0.000 0.000 0.844 0.000 0.008 0.148
#> GSM907855 3 0.2969 0.5334 0.000 0.000 0.776 0.000 0.000 0.224
#> GSM907856 6 0.4141 0.1133 0.000 0.000 0.432 0.012 0.000 0.556
#> GSM907857 6 0.3733 0.3172 0.000 0.000 0.288 0.004 0.008 0.700
#> GSM907825 2 0.3244 0.7381 0.000 0.732 0.000 0.000 0.268 0.000
#> GSM907828 4 0.3616 0.7050 0.000 0.132 0.000 0.792 0.076 0.000
#> GSM907832 2 0.4969 0.6419 0.000 0.616 0.000 0.104 0.280 0.000
#> GSM907833 2 0.5066 0.6376 0.000 0.608 0.000 0.116 0.276 0.000
#> GSM907834 2 0.2340 0.8048 0.000 0.852 0.000 0.000 0.148 0.000
#> GSM907826 2 0.0000 0.8225 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907827 2 0.0405 0.8214 0.000 0.988 0.004 0.008 0.000 0.000
#> GSM907829 6 0.7027 -0.2621 0.084 0.256 0.000 0.000 0.232 0.428
#> GSM907830 4 0.2668 0.7185 0.000 0.168 0.000 0.828 0.004 0.000
#> GSM907831 2 0.2933 0.7784 0.000 0.796 0.004 0.000 0.200 0.000
#> GSM907792 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0858 0.6160 0.000 0.004 0.000 0.000 0.968 0.028
#> GSM907804 1 0.3868 -0.0630 0.504 0.000 0.000 0.000 0.496 0.000
#> GSM907805 1 0.0458 0.8045 0.984 0.000 0.000 0.000 0.000 0.016
#> GSM907806 1 0.0937 0.7895 0.960 0.000 0.000 0.000 0.040 0.000
#> GSM907793 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 1 0.5683 0.2556 0.484 0.000 0.000 0.000 0.168 0.348
#> GSM907796 1 0.5587 0.1635 0.432 0.000 0.000 0.000 0.140 0.428
#> GSM907797 6 0.5877 -0.3711 0.200 0.000 0.000 0.000 0.372 0.428
#> GSM907798 1 0.5587 0.1635 0.432 0.000 0.000 0.000 0.140 0.428
#> GSM907799 1 0.3586 0.6699 0.796 0.000 0.000 0.000 0.080 0.124
#> GSM907800 5 0.5138 0.5341 0.208 0.000 0.000 0.000 0.624 0.168
#> GSM907803 1 0.1349 0.7769 0.940 0.000 0.000 0.000 0.056 0.004
#> GSM907864 4 0.0000 0.8031 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0000 0.8031 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.1116 0.7649 0.000 0.000 0.960 0.004 0.028 0.008
#> GSM907869 6 0.5066 0.3158 0.000 0.000 0.276 0.116 0.000 0.608
#> GSM907870 3 0.4621 0.4439 0.000 0.332 0.612 0.056 0.000 0.000
#> GSM907861 3 0.1141 0.7665 0.000 0.052 0.948 0.000 0.000 0.000
#> GSM907862 3 0.0713 0.7727 0.000 0.000 0.972 0.028 0.000 0.000
#> GSM907863 3 0.0891 0.7755 0.000 0.008 0.968 0.024 0.000 0.000
#> GSM907866 6 0.5636 0.2933 0.000 0.000 0.296 0.024 0.108 0.572
#> GSM907867 3 0.0790 0.7736 0.000 0.032 0.968 0.000 0.000 0.000
#> GSM907839 4 0.0000 0.8031 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907840 4 0.0000 0.8031 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.1204 0.7867 0.000 0.000 0.000 0.944 0.056 0.000
#> GSM907843 4 0.4374 0.6390 0.000 0.096 0.000 0.712 0.192 0.000
#> GSM907845 2 0.3284 0.6772 0.000 0.800 0.000 0.000 0.032 0.168
#> GSM907846 4 0.5143 0.5004 0.000 0.140 0.000 0.612 0.248 0.000
#> GSM907848 2 0.3351 0.7230 0.000 0.712 0.000 0.000 0.288 0.000
#> GSM907851 2 0.4097 0.6405 0.036 0.760 0.000 0.176 0.028 0.000
#> GSM907835 2 0.1204 0.8240 0.000 0.944 0.000 0.000 0.056 0.000
#> GSM907836 2 0.1584 0.8063 0.000 0.928 0.064 0.000 0.008 0.000
#> GSM907837 2 0.0146 0.8222 0.000 0.996 0.004 0.000 0.000 0.000
#> GSM907838 3 0.5074 0.0153 0.000 0.440 0.496 0.056 0.008 0.000
#> GSM907841 6 0.5848 0.1881 0.000 0.000 0.036 0.272 0.120 0.572
#> GSM907844 2 0.0291 0.8220 0.000 0.992 0.004 0.004 0.000 0.000
#> GSM907847 2 0.2003 0.8095 0.000 0.884 0.000 0.000 0.116 0.000
#> GSM907849 2 0.3828 0.0251 0.000 0.560 0.000 0.440 0.000 0.000
#> GSM907850 2 0.0000 0.8225 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.8225 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907853 2 0.1814 0.8143 0.000 0.900 0.000 0.000 0.100 0.000
#> GSM907807 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 4 0.3868 -0.0204 0.496 0.000 0.000 0.504 0.000 0.000
#> GSM907814 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0547 0.8010 0.980 0.000 0.000 0.000 0.020 0.000
#> GSM907818 6 0.6004 -0.2211 0.352 0.000 0.000 0.000 0.240 0.408
#> GSM907819 1 0.5301 0.3604 0.556 0.000 0.000 0.000 0.124 0.320
#> GSM907820 5 0.1958 0.5316 0.004 0.100 0.000 0.000 0.896 0.000
#> GSM907822 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.8094 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2318 0.7524 0.892 0.000 0.000 0.000 0.064 0.044
#> GSM907812 1 0.5587 0.1635 0.432 0.000 0.000 0.000 0.140 0.428
#> GSM907815 6 0.1921 0.2155 0.000 0.000 0.032 0.000 0.052 0.916
#> GSM907817 5 0.4456 0.5839 0.112 0.000 0.000 0.000 0.708 0.180
#> GSM907821 5 0.3835 0.4680 0.000 0.012 0.000 0.000 0.668 0.320
#> GSM907824 5 0.4418 0.5782 0.000 0.192 0.000 0.000 0.708 0.100
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
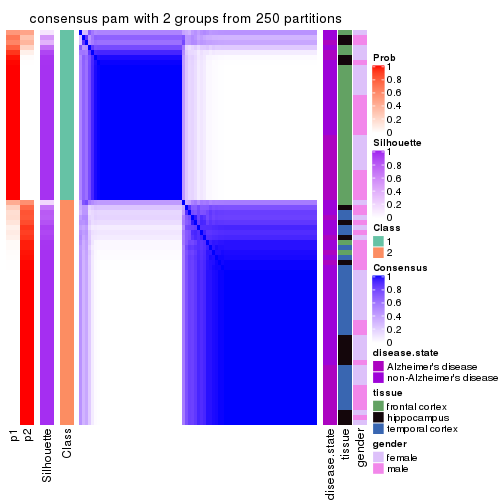
consensus_heatmap(res, k = 3)
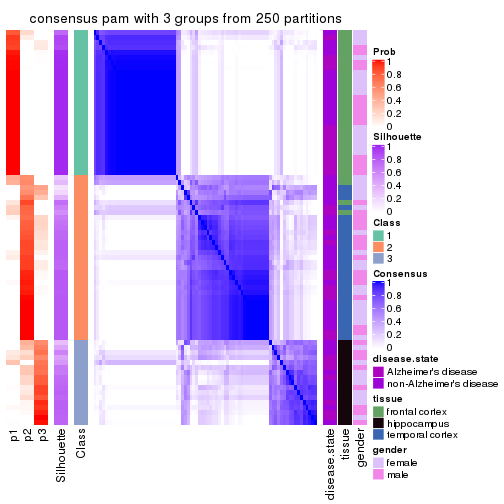
consensus_heatmap(res, k = 4)
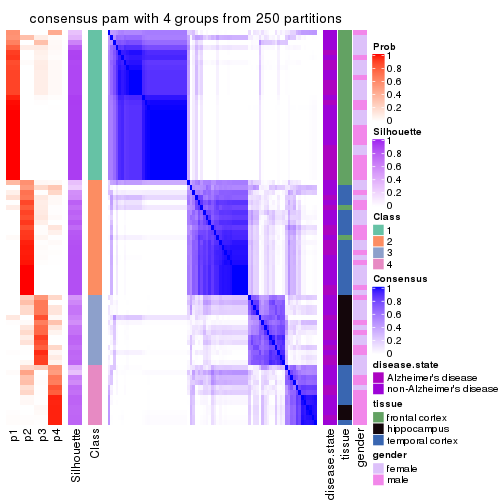
consensus_heatmap(res, k = 5)
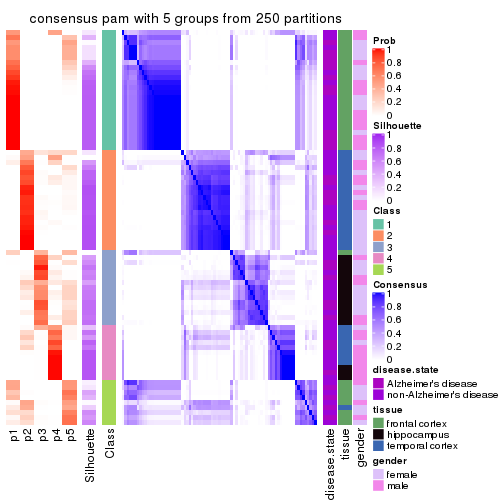
consensus_heatmap(res, k = 6)
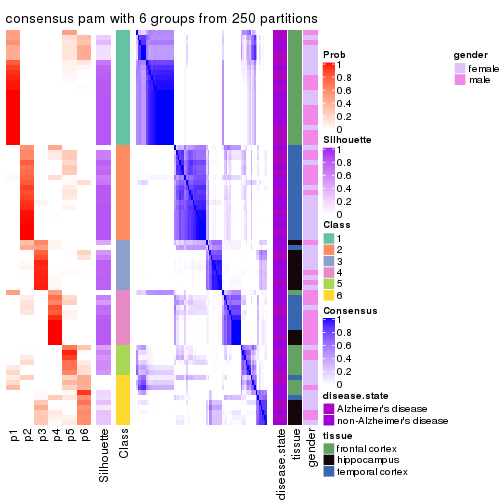
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
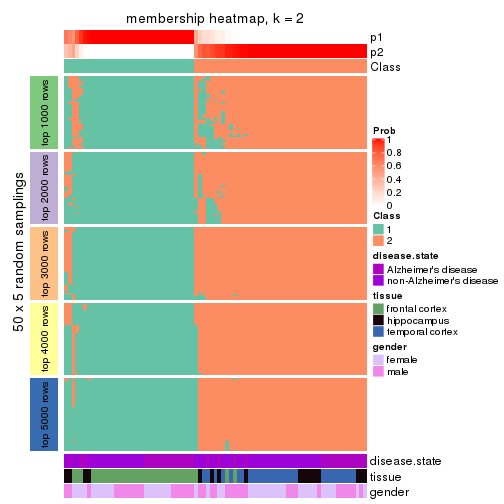
membership_heatmap(res, k = 3)
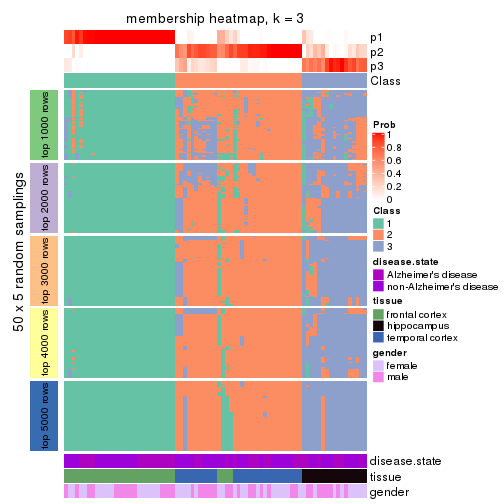
membership_heatmap(res, k = 4)
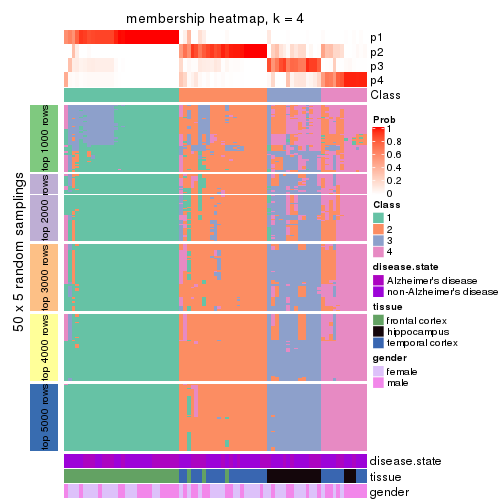
membership_heatmap(res, k = 5)
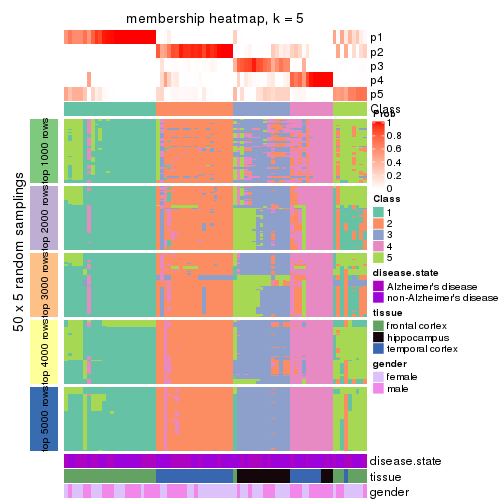
membership_heatmap(res, k = 6)
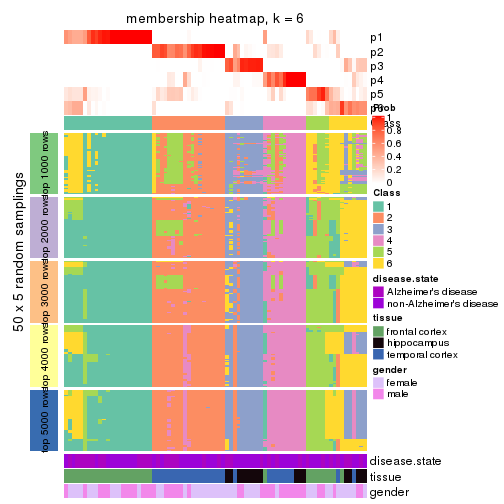
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
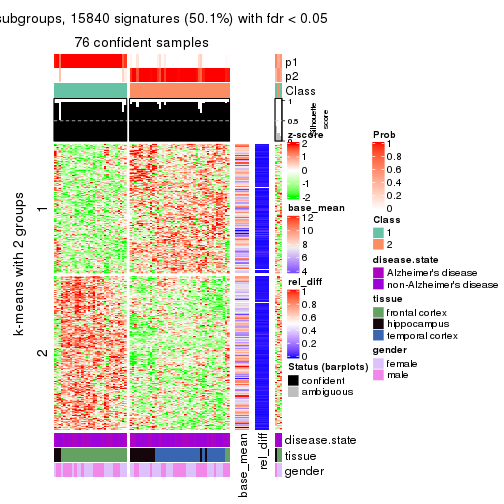
get_signatures(res, k = 3)
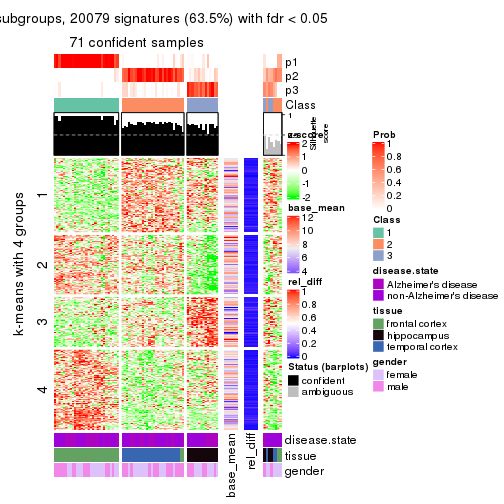
get_signatures(res, k = 4)
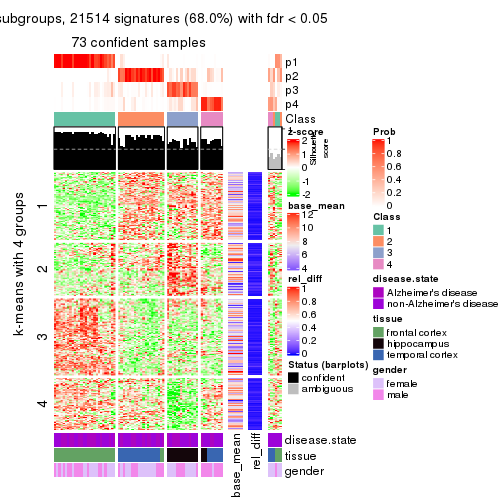
get_signatures(res, k = 5)
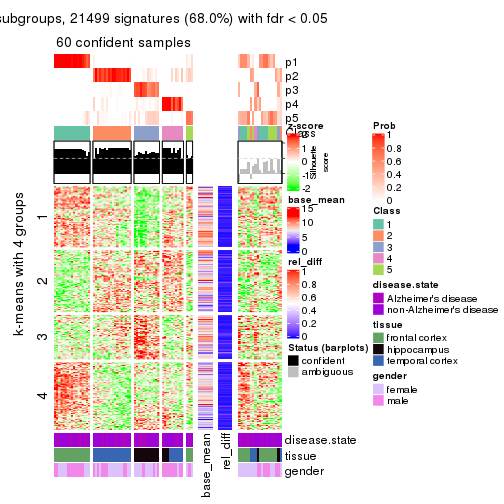
get_signatures(res, k = 6)
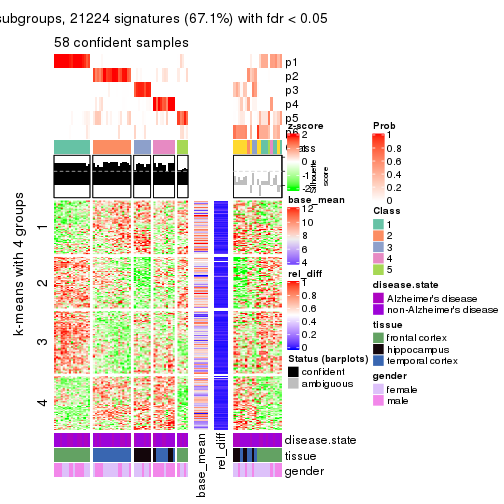
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
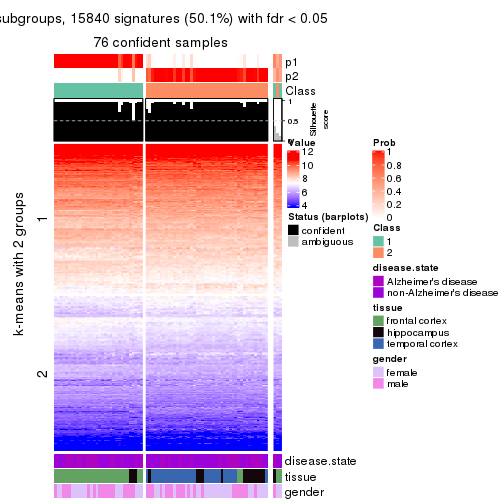
get_signatures(res, k = 3, scale_rows = FALSE)
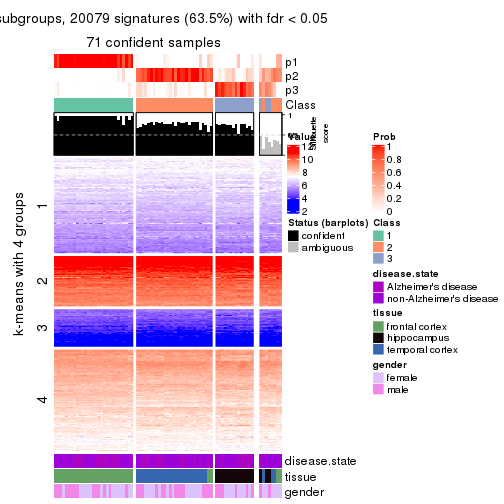
get_signatures(res, k = 4, scale_rows = FALSE)
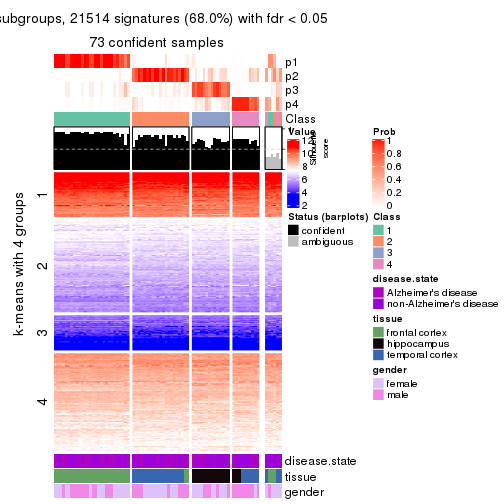
get_signatures(res, k = 5, scale_rows = FALSE)
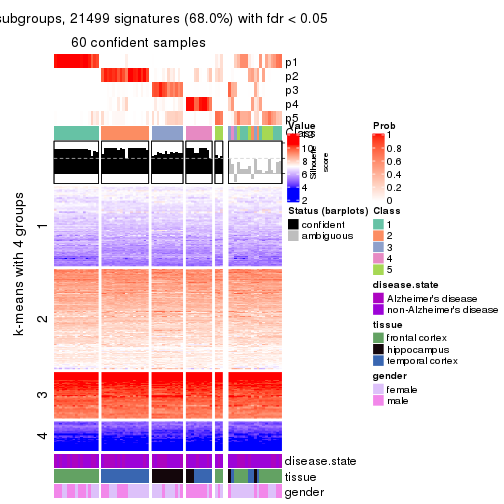
get_signatures(res, k = 6, scale_rows = FALSE)
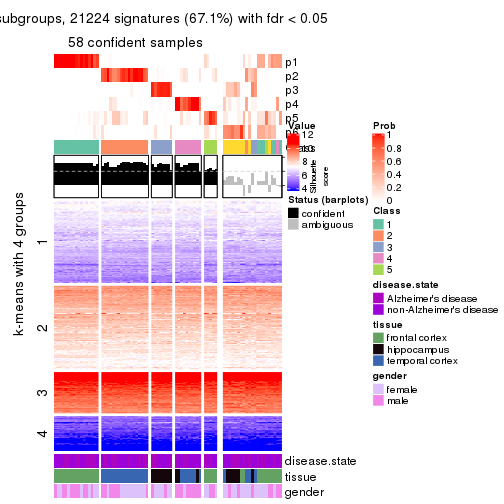
Compare the overlap of signatures from different k:
compare_signatures(res)
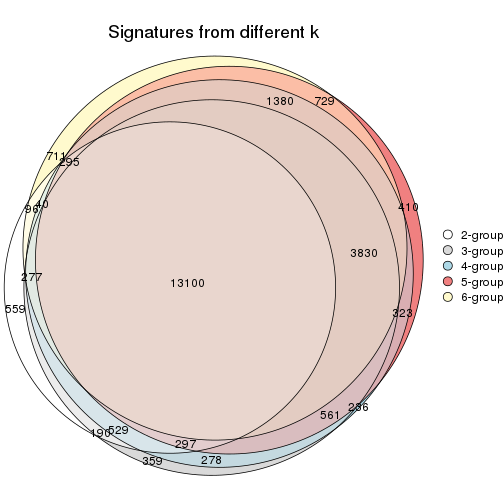
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
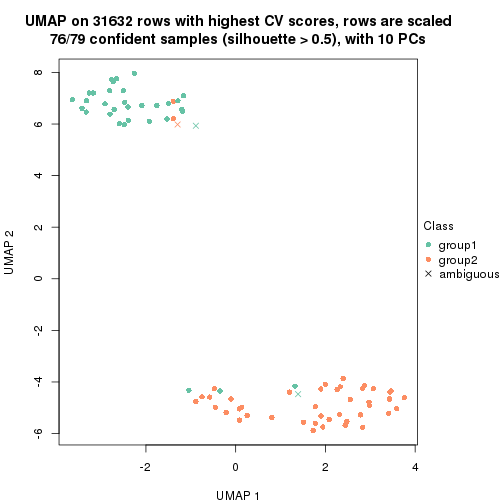
dimension_reduction(res, k = 3, method = "UMAP")
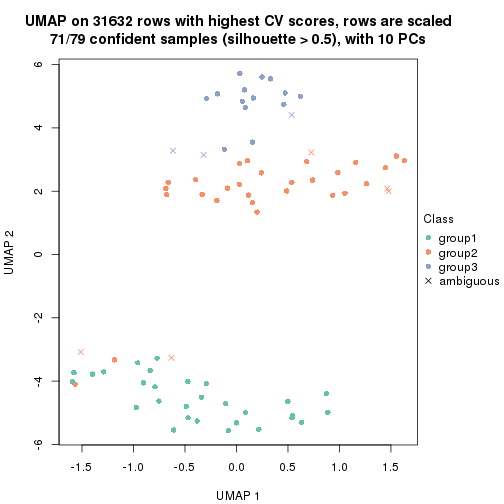
dimension_reduction(res, k = 4, method = "UMAP")
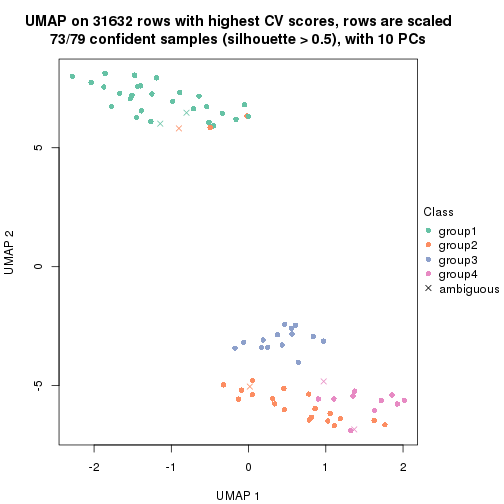
dimension_reduction(res, k = 5, method = "UMAP")
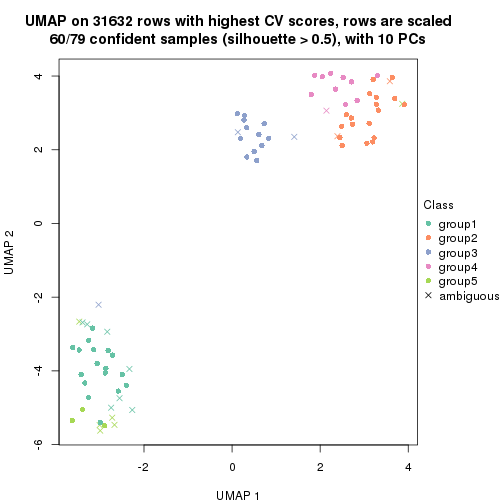
dimension_reduction(res, k = 6, method = "UMAP")
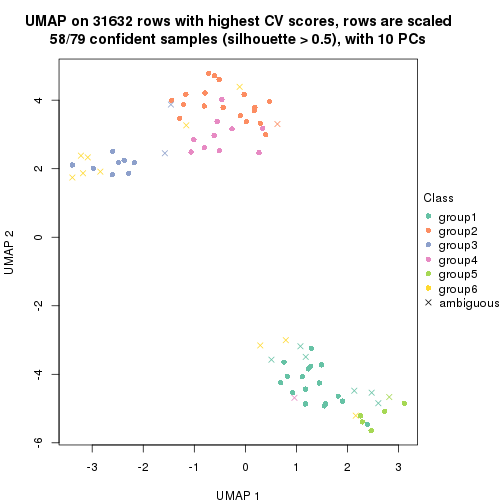
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
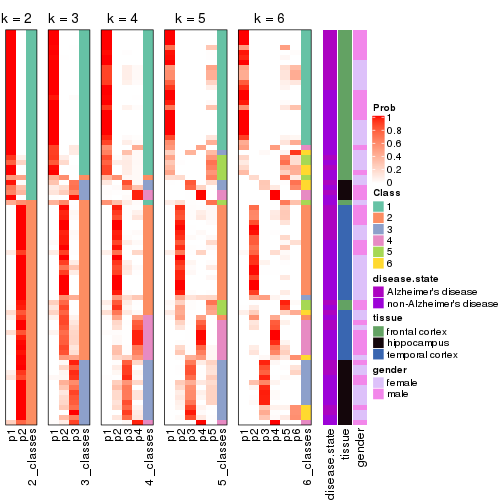
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:pam 76 0.494 2.16e-13 0.8735 2
#> CV:pam 71 0.790 1.04e-27 0.7989 3
#> CV:pam 73 0.747 7.51e-24 0.0439 4
#> CV:pam 60 0.870 1.94e-19 0.0249 5
#> CV:pam 58 0.939 4.16e-18 0.0411 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "mclust"]
# you can also extract it by
# res = res_list["CV:mclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'mclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
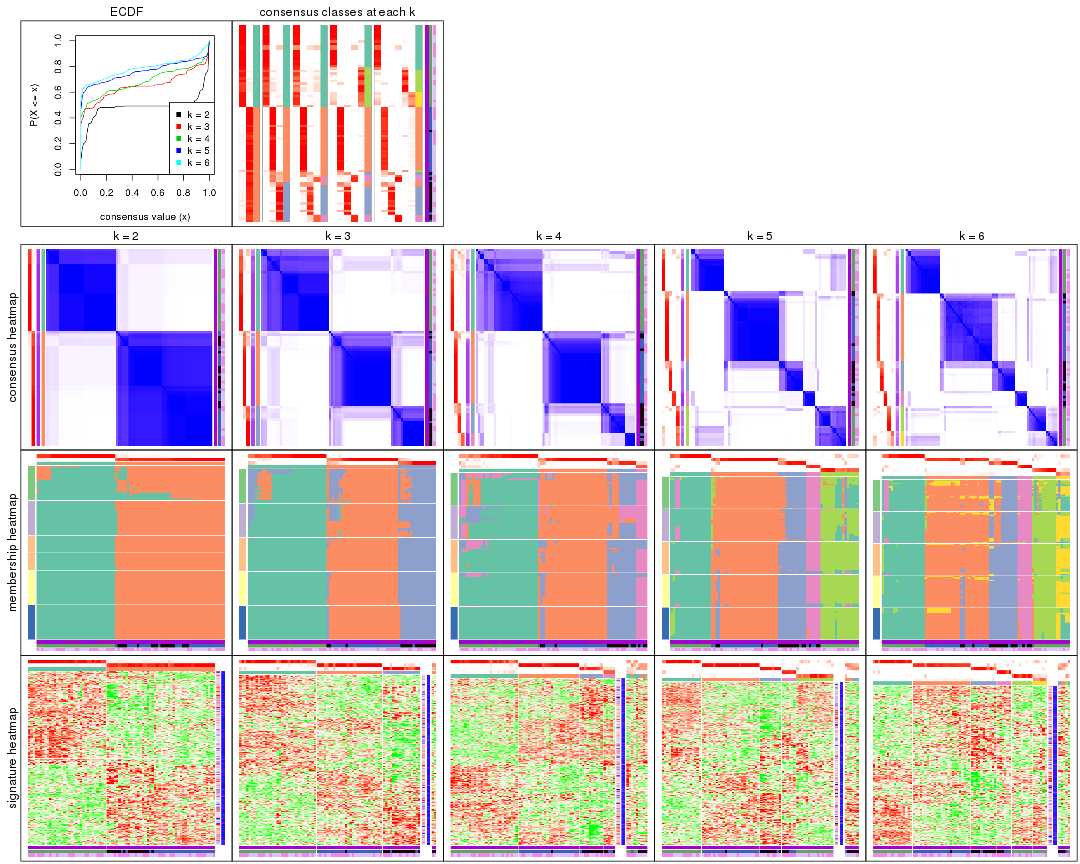
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
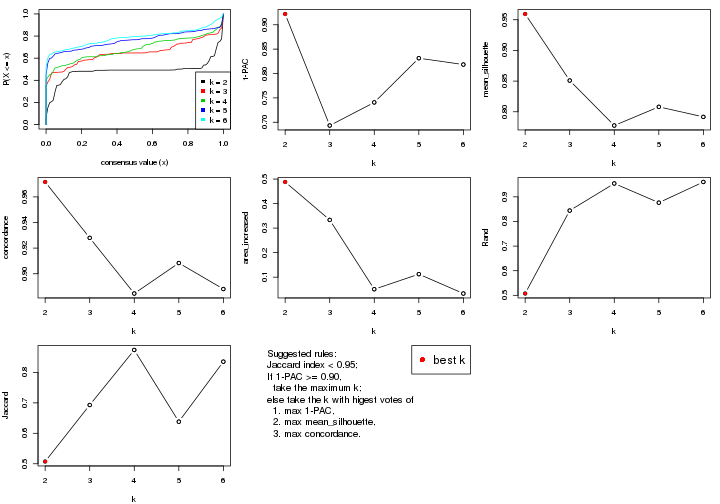
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.922 0.959 0.972 0.4882 0.507 0.507
#> 3 3 0.693 0.851 0.928 0.3335 0.844 0.693
#> 4 4 0.741 0.778 0.885 0.0507 0.954 0.874
#> 5 5 0.831 0.808 0.908 0.1121 0.876 0.638
#> 6 6 0.818 0.792 0.888 0.0332 0.960 0.835
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.2603 0.964 0.044 0.956
#> GSM907859 2 0.4431 0.929 0.092 0.908
#> GSM907860 2 0.2423 0.965 0.040 0.960
#> GSM907854 2 0.2603 0.964 0.044 0.956
#> GSM907855 2 0.2603 0.964 0.044 0.956
#> GSM907856 2 0.2603 0.964 0.044 0.956
#> GSM907857 2 0.5408 0.898 0.124 0.876
#> GSM907825 2 0.0000 0.966 0.000 1.000
#> GSM907828 2 0.0376 0.967 0.004 0.996
#> GSM907832 2 0.0000 0.966 0.000 1.000
#> GSM907833 2 0.0000 0.966 0.000 1.000
#> GSM907834 2 0.0000 0.966 0.000 1.000
#> GSM907826 2 0.0000 0.966 0.000 1.000
#> GSM907827 2 0.0000 0.966 0.000 1.000
#> GSM907829 2 0.8386 0.673 0.268 0.732
#> GSM907830 2 0.2603 0.964 0.044 0.956
#> GSM907831 2 0.0376 0.967 0.004 0.996
#> GSM907792 1 0.0000 0.980 1.000 0.000
#> GSM907795 1 0.0000 0.980 1.000 0.000
#> GSM907801 1 0.0000 0.980 1.000 0.000
#> GSM907802 1 0.4298 0.920 0.912 0.088
#> GSM907804 1 0.0672 0.980 0.992 0.008
#> GSM907805 1 0.0000 0.980 1.000 0.000
#> GSM907806 1 0.0672 0.980 0.992 0.008
#> GSM907793 1 0.0000 0.980 1.000 0.000
#> GSM907794 1 0.0672 0.980 0.992 0.008
#> GSM907796 1 0.0672 0.980 0.992 0.008
#> GSM907797 1 0.0672 0.980 0.992 0.008
#> GSM907798 1 0.0672 0.980 0.992 0.008
#> GSM907799 1 0.0000 0.980 1.000 0.000
#> GSM907800 1 0.4022 0.926 0.920 0.080
#> GSM907803 1 0.0000 0.980 1.000 0.000
#> GSM907864 2 0.2603 0.964 0.044 0.956
#> GSM907865 2 0.5294 0.902 0.120 0.880
#> GSM907868 2 0.2603 0.964 0.044 0.956
#> GSM907869 2 0.5294 0.902 0.120 0.880
#> GSM907870 2 0.0376 0.967 0.004 0.996
#> GSM907861 2 0.0938 0.967 0.012 0.988
#> GSM907862 2 0.1414 0.967 0.020 0.980
#> GSM907863 2 0.0376 0.967 0.004 0.996
#> GSM907866 2 0.2603 0.964 0.044 0.956
#> GSM907867 2 0.0376 0.967 0.004 0.996
#> GSM907839 2 0.2603 0.964 0.044 0.956
#> GSM907840 2 0.2603 0.964 0.044 0.956
#> GSM907842 2 0.2603 0.964 0.044 0.956
#> GSM907843 2 0.1633 0.967 0.024 0.976
#> GSM907845 2 0.4562 0.922 0.096 0.904
#> GSM907846 2 0.2603 0.964 0.044 0.956
#> GSM907848 2 0.0000 0.966 0.000 1.000
#> GSM907851 2 0.2236 0.965 0.036 0.964
#> GSM907835 2 0.0000 0.966 0.000 1.000
#> GSM907836 2 0.0000 0.966 0.000 1.000
#> GSM907837 2 0.0672 0.967 0.008 0.992
#> GSM907838 2 0.0000 0.966 0.000 1.000
#> GSM907841 2 0.2603 0.964 0.044 0.956
#> GSM907844 2 0.0000 0.966 0.000 1.000
#> GSM907847 2 0.0000 0.966 0.000 1.000
#> GSM907849 2 0.2603 0.964 0.044 0.956
#> GSM907850 2 0.0000 0.966 0.000 1.000
#> GSM907852 2 0.0376 0.967 0.004 0.996
#> GSM907853 2 0.0376 0.967 0.004 0.996
#> GSM907807 1 0.0000 0.980 1.000 0.000
#> GSM907813 1 0.0672 0.980 0.992 0.008
#> GSM907814 1 0.0672 0.980 0.992 0.008
#> GSM907816 1 0.0000 0.980 1.000 0.000
#> GSM907818 1 0.0672 0.980 0.992 0.008
#> GSM907819 1 0.0672 0.980 0.992 0.008
#> GSM907820 1 0.5294 0.888 0.880 0.120
#> GSM907822 1 0.0000 0.980 1.000 0.000
#> GSM907823 1 0.0000 0.980 1.000 0.000
#> GSM907808 1 0.0000 0.980 1.000 0.000
#> GSM907809 1 0.0000 0.980 1.000 0.000
#> GSM907810 1 0.0000 0.980 1.000 0.000
#> GSM907811 1 0.0000 0.980 1.000 0.000
#> GSM907812 1 0.0672 0.980 0.992 0.008
#> GSM907815 1 0.0672 0.980 0.992 0.008
#> GSM907817 1 0.4161 0.922 0.916 0.084
#> GSM907821 1 0.4161 0.922 0.916 0.084
#> GSM907824 1 0.4161 0.922 0.916 0.084
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907859 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907860 3 0.4235 0.798 0.000 0.176 0.824
#> GSM907854 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907855 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907856 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907857 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907825 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907828 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907832 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907834 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907826 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907827 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907829 2 0.6679 0.674 0.152 0.748 0.100
#> GSM907830 2 0.5397 0.617 0.000 0.720 0.280
#> GSM907831 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907792 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907802 1 0.4589 0.804 0.820 0.172 0.008
#> GSM907804 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907805 1 0.0424 0.926 0.992 0.000 0.008
#> GSM907806 1 0.0892 0.924 0.980 0.000 0.020
#> GSM907793 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907794 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907796 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907797 1 0.3192 0.870 0.888 0.000 0.112
#> GSM907798 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907799 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907800 1 0.4045 0.861 0.872 0.104 0.024
#> GSM907803 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907864 2 0.5988 0.449 0.000 0.632 0.368
#> GSM907865 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907868 3 0.3038 0.851 0.000 0.104 0.896
#> GSM907869 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907870 2 0.0592 0.909 0.000 0.988 0.012
#> GSM907861 2 0.6215 0.120 0.000 0.572 0.428
#> GSM907862 3 0.4702 0.764 0.000 0.212 0.788
#> GSM907863 3 0.5327 0.686 0.000 0.272 0.728
#> GSM907866 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907867 3 0.5291 0.691 0.000 0.268 0.732
#> GSM907839 2 0.5560 0.584 0.000 0.700 0.300
#> GSM907840 3 0.5431 0.585 0.000 0.284 0.716
#> GSM907842 2 0.5560 0.584 0.000 0.700 0.300
#> GSM907843 2 0.0237 0.914 0.000 0.996 0.004
#> GSM907845 2 0.1751 0.889 0.012 0.960 0.028
#> GSM907846 2 0.3038 0.832 0.000 0.896 0.104
#> GSM907848 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907851 2 0.0237 0.914 0.004 0.996 0.000
#> GSM907835 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907836 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907837 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907838 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907841 3 0.0000 0.902 0.000 0.000 1.000
#> GSM907844 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907849 2 0.0424 0.911 0.008 0.992 0.000
#> GSM907850 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907853 2 0.0000 0.917 0.000 1.000 0.000
#> GSM907807 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907813 1 0.5560 0.642 0.700 0.000 0.300
#> GSM907814 1 0.5560 0.642 0.700 0.000 0.300
#> GSM907816 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907818 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907819 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907820 1 0.4291 0.799 0.820 0.180 0.000
#> GSM907822 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.927 1.000 0.000 0.000
#> GSM907812 1 0.1163 0.923 0.972 0.000 0.028
#> GSM907815 1 0.5926 0.549 0.644 0.000 0.356
#> GSM907817 1 0.4270 0.852 0.860 0.116 0.024
#> GSM907821 1 0.4874 0.824 0.828 0.144 0.028
#> GSM907824 1 0.4862 0.812 0.820 0.160 0.020
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.1389 0.7154 0.000 0.048 0.952 0.000
#> GSM907859 4 0.3569 0.9909 0.000 0.000 0.196 0.804
#> GSM907860 3 0.4790 0.5240 0.000 0.380 0.620 0.000
#> GSM907854 3 0.2814 0.6920 0.000 0.132 0.868 0.000
#> GSM907855 3 0.1302 0.7153 0.000 0.044 0.956 0.000
#> GSM907856 3 0.1022 0.7109 0.000 0.032 0.968 0.000
#> GSM907857 3 0.1151 0.6743 0.000 0.008 0.968 0.024
#> GSM907825 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907828 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907832 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907833 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907834 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907826 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907827 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907829 2 0.2861 0.8390 0.012 0.908 0.032 0.048
#> GSM907830 2 0.3172 0.7329 0.000 0.840 0.160 0.000
#> GSM907831 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907792 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907795 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907801 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907802 1 0.7461 0.5863 0.604 0.192 0.032 0.172
#> GSM907804 1 0.1284 0.8648 0.964 0.000 0.024 0.012
#> GSM907805 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907806 1 0.2197 0.8570 0.928 0.000 0.024 0.048
#> GSM907793 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907794 1 0.2976 0.8337 0.872 0.000 0.008 0.120
#> GSM907796 1 0.1635 0.8623 0.948 0.000 0.008 0.044
#> GSM907797 1 0.2831 0.8019 0.876 0.000 0.120 0.004
#> GSM907798 1 0.1635 0.8623 0.948 0.000 0.008 0.044
#> GSM907799 1 0.0469 0.8684 0.988 0.000 0.000 0.012
#> GSM907800 1 0.5719 0.7429 0.732 0.044 0.032 0.192
#> GSM907803 1 0.0469 0.8681 0.988 0.000 0.000 0.012
#> GSM907864 4 0.3710 0.9886 0.000 0.004 0.192 0.804
#> GSM907865 4 0.3569 0.9909 0.000 0.000 0.196 0.804
#> GSM907868 3 0.4304 0.6108 0.000 0.284 0.716 0.000
#> GSM907869 3 0.1151 0.6743 0.000 0.008 0.968 0.024
#> GSM907870 2 0.0707 0.9066 0.000 0.980 0.020 0.000
#> GSM907861 2 0.4955 -0.0917 0.000 0.556 0.444 0.000
#> GSM907862 3 0.4985 0.3156 0.000 0.468 0.532 0.000
#> GSM907863 2 0.4981 -0.1693 0.000 0.536 0.464 0.000
#> GSM907866 3 0.1022 0.7109 0.000 0.032 0.968 0.000
#> GSM907867 3 0.4907 0.4461 0.000 0.420 0.580 0.000
#> GSM907839 4 0.4012 0.9733 0.000 0.016 0.184 0.800
#> GSM907840 4 0.3569 0.9909 0.000 0.000 0.196 0.804
#> GSM907842 2 0.6903 0.2904 0.000 0.592 0.184 0.224
#> GSM907843 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907845 2 0.1492 0.8875 0.004 0.956 0.004 0.036
#> GSM907846 2 0.1118 0.8921 0.000 0.964 0.036 0.000
#> GSM907848 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907851 2 0.0592 0.9109 0.000 0.984 0.016 0.000
#> GSM907835 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907836 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907837 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907838 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907841 3 0.1022 0.7109 0.000 0.032 0.968 0.000
#> GSM907844 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907847 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907849 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907850 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907853 2 0.0000 0.9244 0.000 1.000 0.000 0.000
#> GSM907807 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907813 1 0.7159 0.3126 0.548 0.000 0.180 0.272
#> GSM907814 1 0.7159 0.3126 0.548 0.000 0.180 0.272
#> GSM907816 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907818 1 0.2546 0.8467 0.900 0.000 0.008 0.092
#> GSM907819 1 0.1635 0.8623 0.948 0.000 0.008 0.044
#> GSM907820 1 0.8045 0.3608 0.480 0.336 0.032 0.152
#> GSM907822 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907823 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907808 1 0.0000 0.8680 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0469 0.8682 0.988 0.000 0.000 0.012
#> GSM907810 1 0.0188 0.8678 0.996 0.000 0.000 0.004
#> GSM907811 1 0.0707 0.8674 0.980 0.000 0.000 0.020
#> GSM907812 1 0.1635 0.8623 0.948 0.000 0.008 0.044
#> GSM907815 1 0.4981 0.3477 0.536 0.000 0.464 0.000
#> GSM907817 1 0.5719 0.7431 0.732 0.044 0.032 0.192
#> GSM907821 1 0.7309 0.6200 0.620 0.156 0.032 0.192
#> GSM907824 1 0.7353 0.6118 0.616 0.164 0.032 0.188
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0404 0.799 0.000 0.012 0.988 0.000 0.000
#> GSM907859 4 0.1331 0.970 0.000 0.008 0.040 0.952 0.000
#> GSM907860 3 0.4161 0.461 0.000 0.392 0.608 0.000 0.000
#> GSM907854 3 0.0609 0.796 0.000 0.020 0.980 0.000 0.000
#> GSM907855 3 0.0290 0.799 0.000 0.008 0.992 0.000 0.000
#> GSM907856 3 0.0451 0.797 0.000 0.008 0.988 0.004 0.000
#> GSM907857 3 0.0324 0.790 0.000 0.000 0.992 0.004 0.004
#> GSM907825 2 0.0162 0.935 0.000 0.996 0.000 0.000 0.004
#> GSM907828 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907832 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907833 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907834 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907826 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907827 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907829 2 0.4457 0.420 0.000 0.620 0.012 0.000 0.368
#> GSM907830 2 0.1205 0.893 0.000 0.956 0.040 0.004 0.000
#> GSM907831 2 0.0162 0.934 0.000 0.996 0.004 0.000 0.000
#> GSM907792 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0963 0.760 0.000 0.036 0.000 0.000 0.964
#> GSM907804 5 0.3966 0.678 0.336 0.000 0.000 0.000 0.664
#> GSM907805 1 0.0290 0.915 0.992 0.000 0.000 0.000 0.008
#> GSM907806 5 0.3876 0.703 0.316 0.000 0.000 0.000 0.684
#> GSM907793 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.1768 0.793 0.072 0.000 0.004 0.000 0.924
#> GSM907796 5 0.3430 0.785 0.220 0.000 0.004 0.000 0.776
#> GSM907797 5 0.4446 0.787 0.196 0.000 0.012 0.040 0.752
#> GSM907798 5 0.3398 0.787 0.216 0.000 0.004 0.000 0.780
#> GSM907799 1 0.0609 0.907 0.980 0.000 0.000 0.000 0.020
#> GSM907800 5 0.0290 0.771 0.000 0.008 0.000 0.000 0.992
#> GSM907803 1 0.3336 0.603 0.772 0.000 0.000 0.000 0.228
#> GSM907864 4 0.1331 0.970 0.000 0.008 0.040 0.952 0.000
#> GSM907865 4 0.1043 0.966 0.000 0.000 0.040 0.960 0.000
#> GSM907868 3 0.2561 0.715 0.000 0.144 0.856 0.000 0.000
#> GSM907869 3 0.0324 0.790 0.000 0.000 0.992 0.004 0.004
#> GSM907870 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907861 3 0.4219 0.411 0.000 0.416 0.584 0.000 0.000
#> GSM907862 2 0.4294 -0.112 0.000 0.532 0.468 0.000 0.000
#> GSM907863 2 0.4074 0.282 0.000 0.636 0.364 0.000 0.000
#> GSM907866 3 0.0290 0.799 0.000 0.008 0.992 0.000 0.000
#> GSM907867 3 0.4192 0.437 0.000 0.404 0.596 0.000 0.000
#> GSM907839 4 0.1331 0.970 0.000 0.008 0.040 0.952 0.000
#> GSM907840 4 0.1043 0.966 0.000 0.000 0.040 0.960 0.000
#> GSM907842 4 0.2927 0.868 0.000 0.092 0.040 0.868 0.000
#> GSM907843 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907845 2 0.2462 0.819 0.000 0.880 0.008 0.000 0.112
#> GSM907846 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907848 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907851 2 0.0510 0.925 0.000 0.984 0.000 0.000 0.016
#> GSM907835 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907837 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907841 3 0.0290 0.799 0.000 0.008 0.992 0.000 0.000
#> GSM907844 2 0.0162 0.935 0.000 0.996 0.000 0.000 0.004
#> GSM907847 2 0.0000 0.936 0.000 1.000 0.000 0.000 0.000
#> GSM907849 2 0.0510 0.925 0.000 0.984 0.000 0.000 0.016
#> GSM907850 2 0.0162 0.935 0.000 0.996 0.000 0.000 0.004
#> GSM907852 2 0.0162 0.935 0.000 0.996 0.000 0.000 0.004
#> GSM907853 2 0.0162 0.935 0.000 0.996 0.000 0.000 0.004
#> GSM907807 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.3913 0.518 0.676 0.000 0.000 0.324 0.000
#> GSM907814 1 0.3857 0.537 0.688 0.000 0.000 0.312 0.000
#> GSM907816 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.3010 0.801 0.172 0.000 0.004 0.000 0.824
#> GSM907819 5 0.3607 0.770 0.244 0.000 0.004 0.000 0.752
#> GSM907820 5 0.3480 0.558 0.000 0.248 0.000 0.000 0.752
#> GSM907822 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0404 0.912 0.988 0.000 0.000 0.000 0.012
#> GSM907810 1 0.0000 0.919 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2732 0.735 0.840 0.000 0.000 0.000 0.160
#> GSM907812 5 0.4310 0.569 0.392 0.000 0.004 0.000 0.604
#> GSM907815 5 0.5137 0.531 0.004 0.000 0.340 0.044 0.612
#> GSM907817 5 0.0290 0.771 0.000 0.008 0.000 0.000 0.992
#> GSM907821 5 0.0290 0.771 0.000 0.008 0.000 0.000 0.992
#> GSM907824 5 0.0404 0.770 0.000 0.012 0.000 0.000 0.988
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0260 0.823 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907859 4 0.0260 0.925 0.000 0.000 0.000 0.992 0.000 0.008
#> GSM907860 3 0.4438 0.522 0.000 0.328 0.628 0.000 0.000 0.044
#> GSM907854 3 0.0405 0.822 0.000 0.008 0.988 0.000 0.000 0.004
#> GSM907855 3 0.0260 0.823 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907856 3 0.0260 0.823 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907857 3 0.2003 0.767 0.000 0.000 0.884 0.000 0.000 0.116
#> GSM907825 2 0.1588 0.902 0.000 0.924 0.000 0.000 0.004 0.072
#> GSM907828 2 0.1267 0.897 0.000 0.940 0.000 0.000 0.000 0.060
#> GSM907832 2 0.0858 0.909 0.000 0.968 0.000 0.000 0.004 0.028
#> GSM907833 2 0.0547 0.907 0.000 0.980 0.000 0.000 0.000 0.020
#> GSM907834 2 0.1644 0.901 0.000 0.920 0.000 0.000 0.004 0.076
#> GSM907826 2 0.1588 0.901 0.000 0.924 0.000 0.000 0.004 0.072
#> GSM907827 2 0.1644 0.905 0.000 0.920 0.000 0.000 0.004 0.076
#> GSM907829 5 0.4796 0.277 0.000 0.396 0.020 0.000 0.560 0.024
#> GSM907830 2 0.1923 0.890 0.000 0.916 0.016 0.004 0.000 0.064
#> GSM907831 2 0.1845 0.900 0.000 0.916 0.008 0.000 0.004 0.072
#> GSM907792 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.914 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907802 5 0.0909 0.784 0.000 0.020 0.000 0.000 0.968 0.012
#> GSM907804 1 0.3620 0.268 0.648 0.000 0.000 0.000 0.352 0.000
#> GSM907805 1 0.0000 0.914 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907806 5 0.3050 0.500 0.236 0.000 0.000 0.000 0.764 0.000
#> GSM907793 1 0.0000 0.914 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.1398 0.751 0.052 0.000 0.000 0.000 0.940 0.008
#> GSM907796 6 0.5530 0.761 0.220 0.000 0.000 0.000 0.220 0.560
#> GSM907797 6 0.4246 0.672 0.096 0.000 0.012 0.000 0.136 0.756
#> GSM907798 6 0.5529 0.756 0.212 0.000 0.000 0.000 0.228 0.560
#> GSM907799 1 0.0363 0.909 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907800 5 0.0000 0.792 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907803 1 0.1141 0.870 0.948 0.000 0.000 0.000 0.052 0.000
#> GSM907864 4 0.0000 0.927 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0000 0.927 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.1297 0.808 0.000 0.040 0.948 0.000 0.000 0.012
#> GSM907869 3 0.2260 0.755 0.000 0.000 0.860 0.000 0.000 0.140
#> GSM907870 2 0.1075 0.902 0.000 0.952 0.000 0.000 0.000 0.048
#> GSM907861 3 0.4465 0.521 0.000 0.332 0.628 0.000 0.004 0.036
#> GSM907862 2 0.4756 -0.120 0.000 0.488 0.464 0.000 0.000 0.048
#> GSM907863 2 0.4631 0.297 0.000 0.596 0.352 0.000 0.000 0.052
#> GSM907866 3 0.0000 0.817 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907867 3 0.4490 0.469 0.000 0.360 0.604 0.000 0.004 0.032
#> GSM907839 4 0.0547 0.915 0.000 0.020 0.000 0.980 0.000 0.000
#> GSM907840 4 0.0000 0.927 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.3523 0.677 0.000 0.180 0.000 0.780 0.000 0.040
#> GSM907843 2 0.1531 0.893 0.000 0.928 0.000 0.004 0.000 0.068
#> GSM907845 2 0.3514 0.670 0.000 0.752 0.000 0.000 0.228 0.020
#> GSM907846 2 0.1682 0.894 0.000 0.928 0.020 0.000 0.000 0.052
#> GSM907848 2 0.0363 0.910 0.000 0.988 0.000 0.000 0.000 0.012
#> GSM907851 2 0.1493 0.897 0.004 0.936 0.000 0.004 0.000 0.056
#> GSM907835 2 0.1531 0.902 0.000 0.928 0.000 0.000 0.004 0.068
#> GSM907836 2 0.0858 0.910 0.000 0.968 0.000 0.000 0.004 0.028
#> GSM907837 2 0.1444 0.905 0.000 0.928 0.000 0.000 0.000 0.072
#> GSM907838 2 0.1204 0.906 0.000 0.944 0.000 0.000 0.000 0.056
#> GSM907841 3 0.0260 0.823 0.000 0.008 0.992 0.000 0.000 0.000
#> GSM907844 2 0.1644 0.901 0.000 0.920 0.000 0.000 0.004 0.076
#> GSM907847 2 0.0865 0.905 0.000 0.964 0.000 0.000 0.000 0.036
#> GSM907849 2 0.1364 0.901 0.004 0.944 0.000 0.004 0.000 0.048
#> GSM907850 2 0.1010 0.908 0.000 0.960 0.000 0.000 0.004 0.036
#> GSM907852 2 0.1531 0.902 0.000 0.928 0.000 0.000 0.004 0.068
#> GSM907853 2 0.1152 0.907 0.000 0.952 0.000 0.000 0.004 0.044
#> GSM907807 1 0.0000 0.914 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.3240 0.626 0.752 0.000 0.000 0.244 0.000 0.004
#> GSM907814 1 0.3215 0.630 0.756 0.000 0.000 0.240 0.000 0.004
#> GSM907816 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907818 5 0.2462 0.686 0.096 0.000 0.000 0.000 0.876 0.028
#> GSM907819 6 0.5770 0.731 0.288 0.000 0.000 0.000 0.212 0.500
#> GSM907820 5 0.3229 0.622 0.004 0.172 0.000 0.000 0.804 0.020
#> GSM907822 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907823 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907808 1 0.0603 0.905 0.980 0.000 0.000 0.000 0.004 0.016
#> GSM907809 1 0.1049 0.890 0.960 0.000 0.000 0.000 0.008 0.032
#> GSM907810 1 0.0146 0.914 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907811 1 0.1075 0.876 0.952 0.000 0.000 0.000 0.048 0.000
#> GSM907812 6 0.5456 0.641 0.372 0.000 0.000 0.000 0.128 0.500
#> GSM907815 6 0.3784 0.504 0.000 0.000 0.144 0.000 0.080 0.776
#> GSM907817 5 0.0000 0.792 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907821 5 0.0000 0.792 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907824 5 0.0405 0.791 0.000 0.004 0.000 0.000 0.988 0.008
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
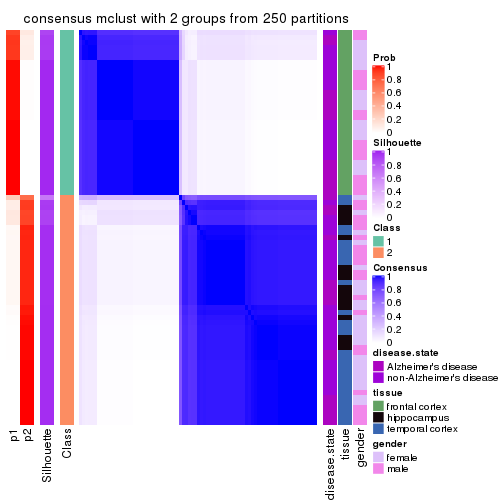
consensus_heatmap(res, k = 3)
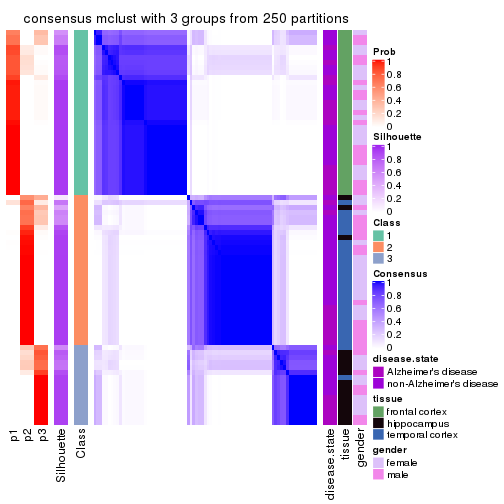
consensus_heatmap(res, k = 4)
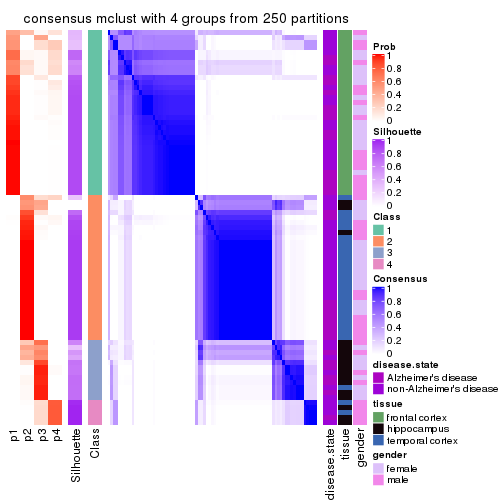
consensus_heatmap(res, k = 5)
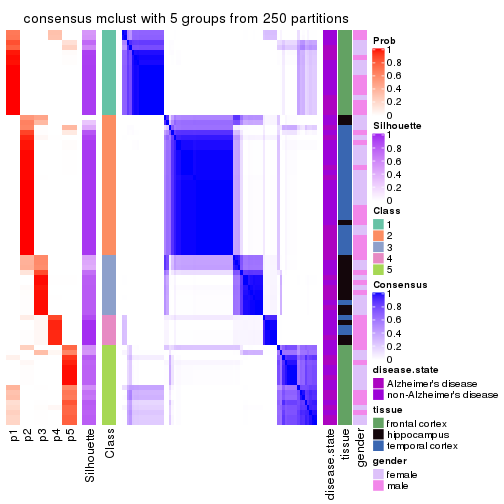
consensus_heatmap(res, k = 6)
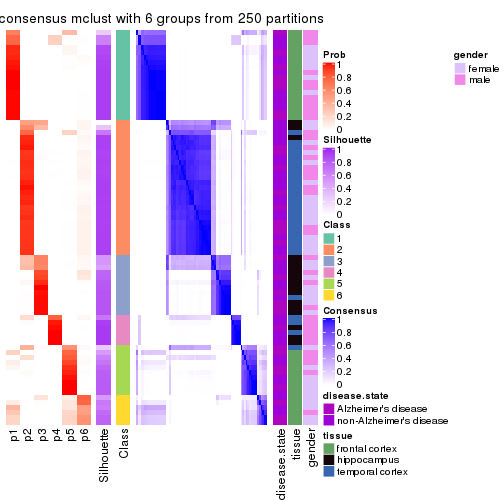
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
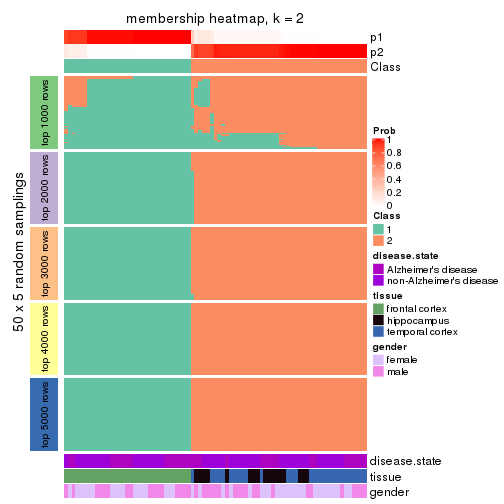
membership_heatmap(res, k = 3)
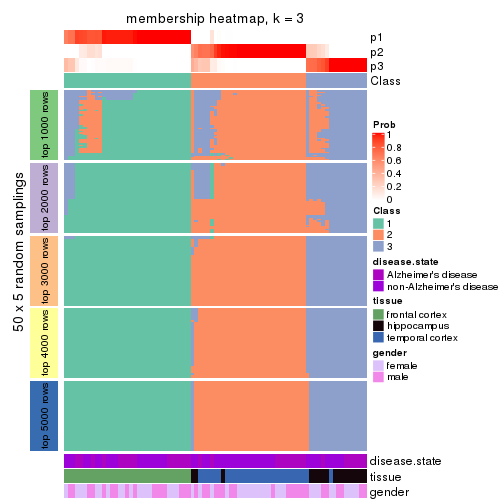
membership_heatmap(res, k = 4)
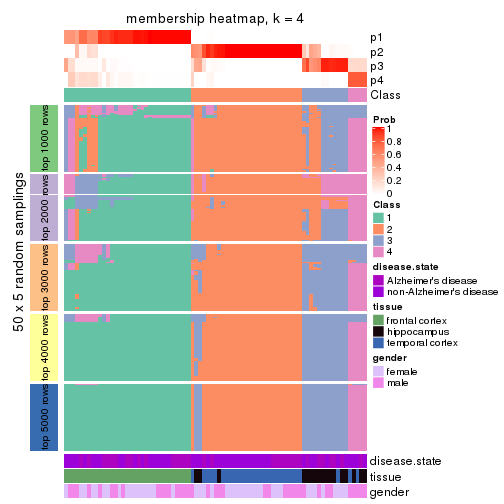
membership_heatmap(res, k = 5)
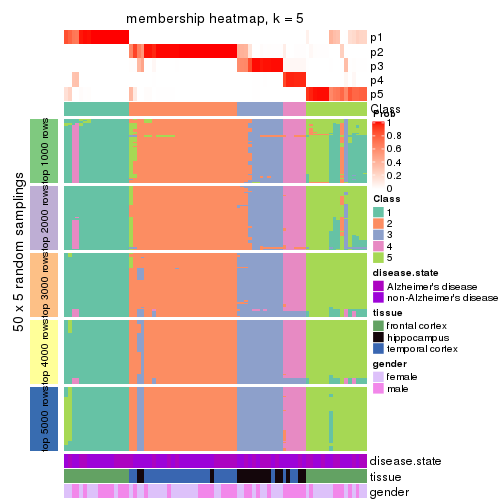
membership_heatmap(res, k = 6)
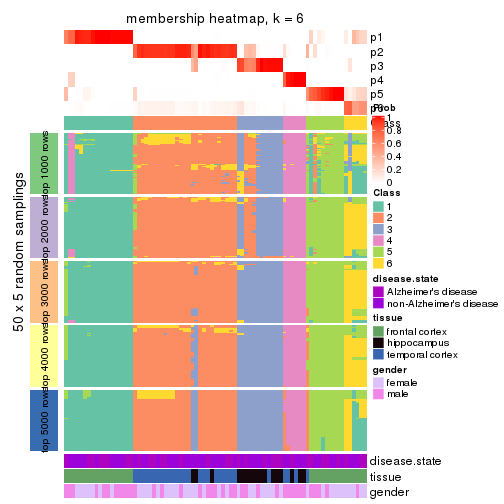
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
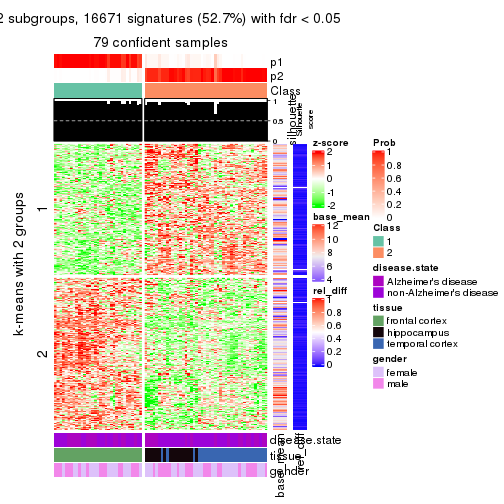
get_signatures(res, k = 3)
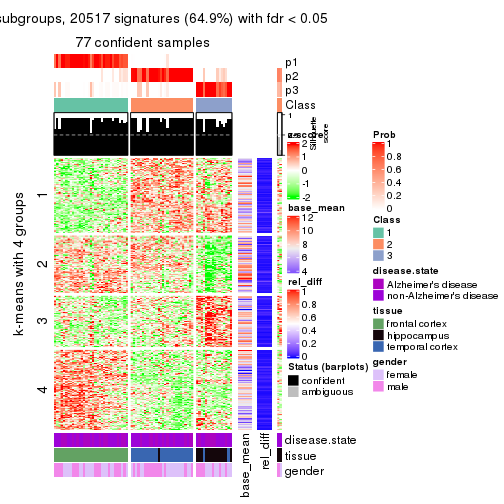
get_signatures(res, k = 4)
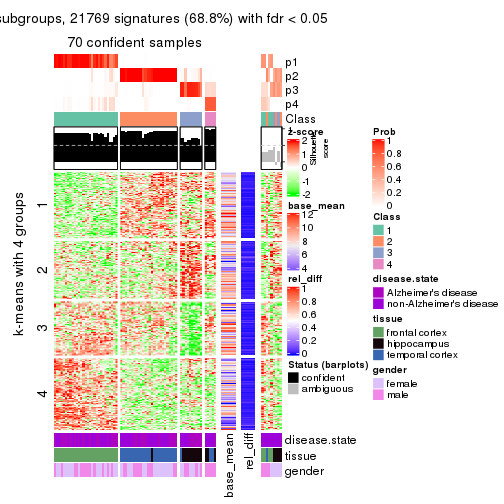
get_signatures(res, k = 5)
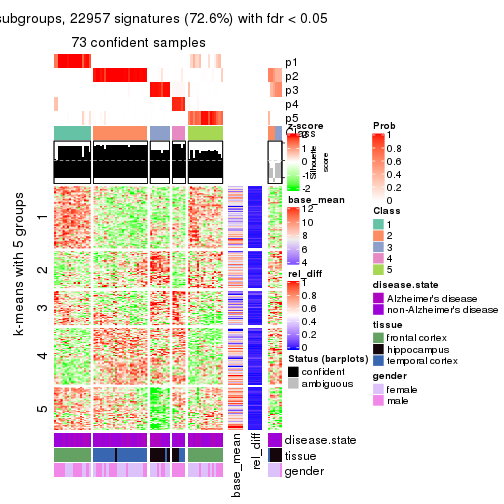
get_signatures(res, k = 6)
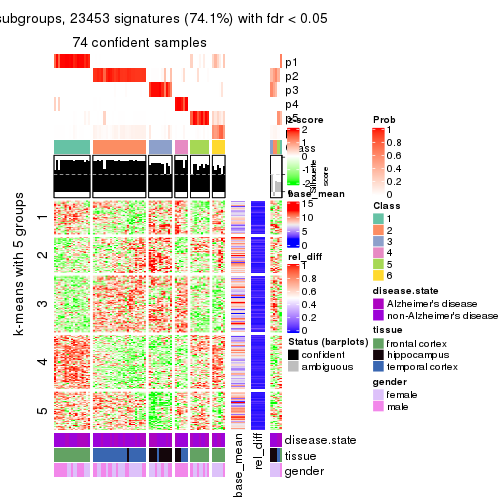
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
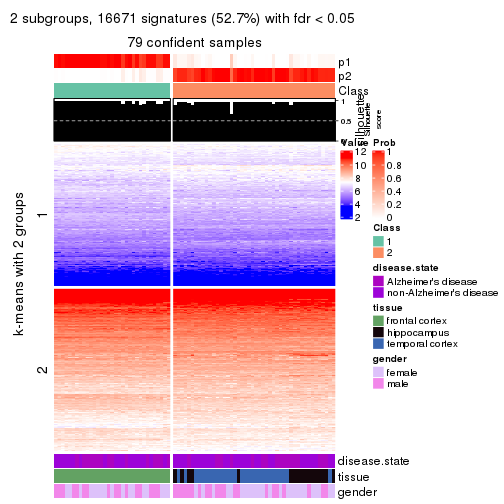
get_signatures(res, k = 3, scale_rows = FALSE)
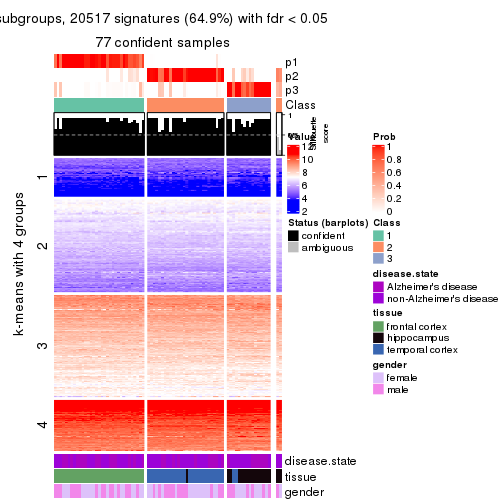
get_signatures(res, k = 4, scale_rows = FALSE)
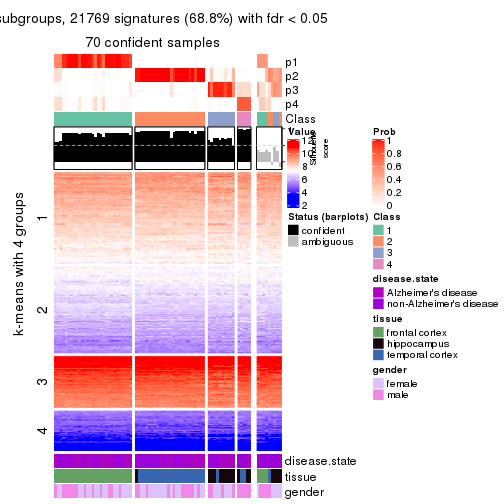
get_signatures(res, k = 5, scale_rows = FALSE)
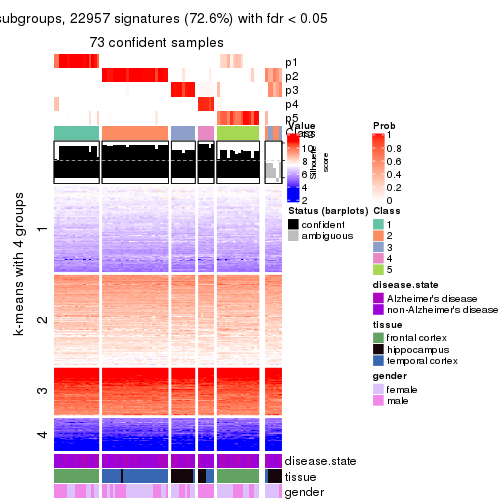
get_signatures(res, k = 6, scale_rows = FALSE)
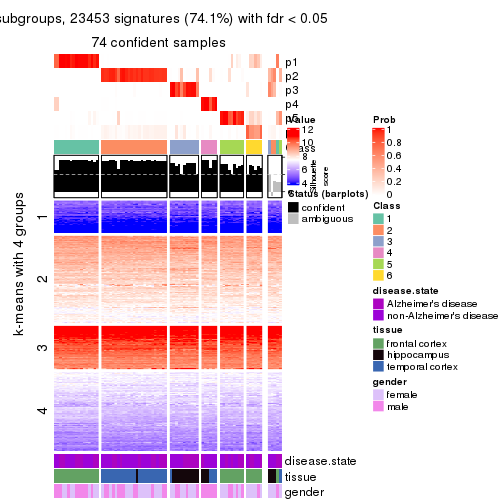
Compare the overlap of signatures from different k:
compare_signatures(res)
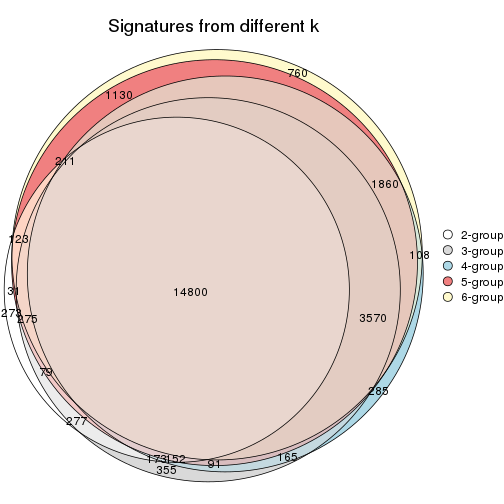
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
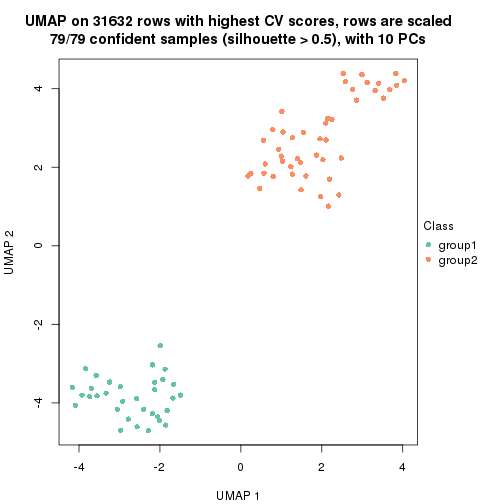
dimension_reduction(res, k = 3, method = "UMAP")
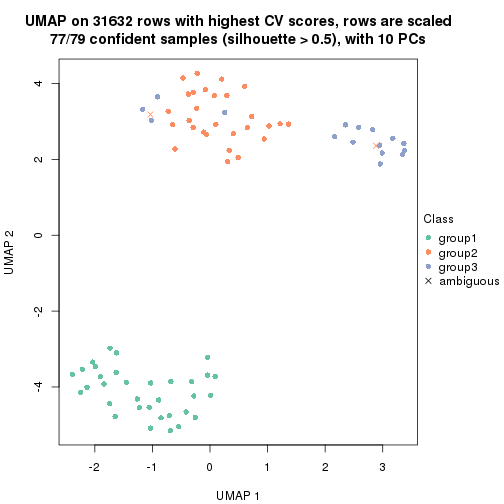
dimension_reduction(res, k = 4, method = "UMAP")
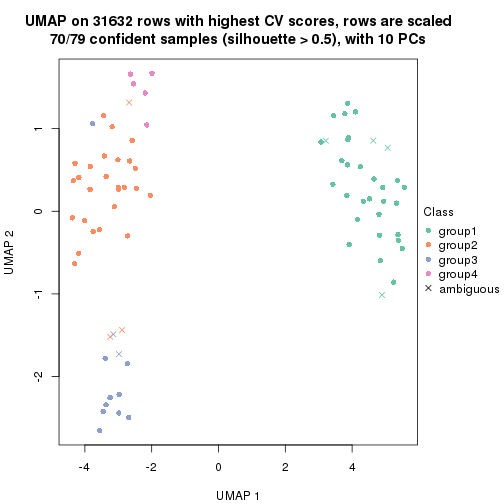
dimension_reduction(res, k = 5, method = "UMAP")
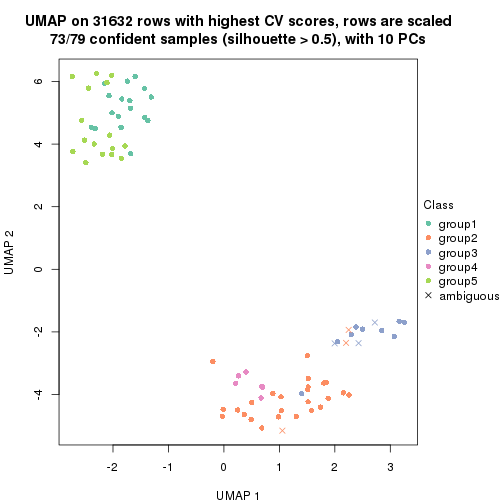
dimension_reduction(res, k = 6, method = "UMAP")
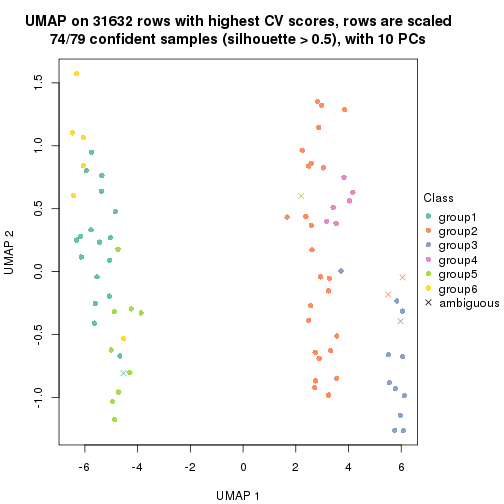
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
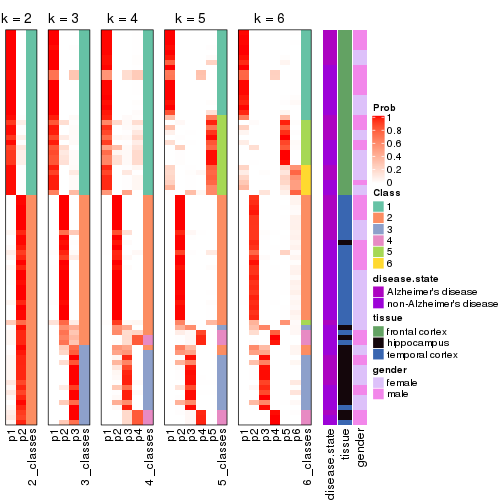
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:mclust 79 0.599 7.00e-18 0.9838 2
#> CV:mclust 77 0.729 9.52e-28 0.9518 3
#> CV:mclust 70 0.372 1.20e-22 0.1060 4
#> CV:mclust 73 0.550 1.45e-21 0.0642 5
#> CV:mclust 74 0.729 2.77e-21 0.0637 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["CV", "NMF"]
# you can also extract it by
# res = res_list["CV:NMF"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'CV' method.
#> Subgroups are detected by 'NMF' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
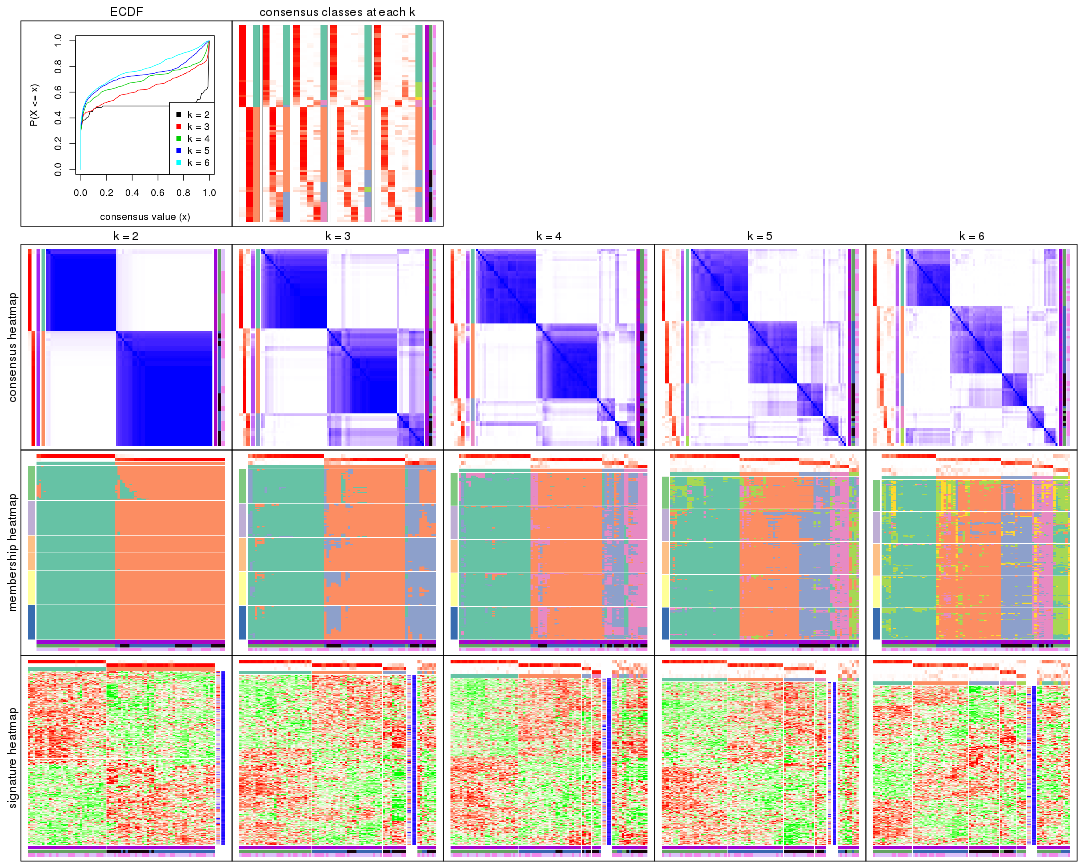
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
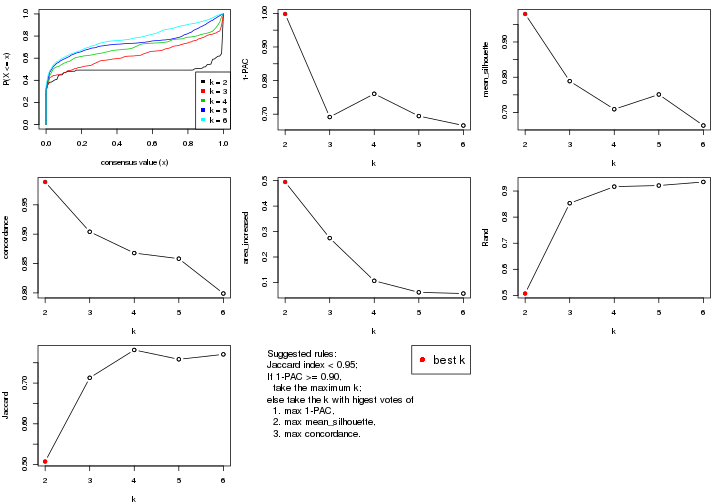
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.998 0.980 0.989 0.4948 0.507 0.507
#> 3 3 0.692 0.789 0.904 0.2743 0.853 0.713
#> 4 4 0.761 0.709 0.868 0.1065 0.917 0.781
#> 5 5 0.694 0.751 0.858 0.0612 0.921 0.758
#> 6 6 0.666 0.663 0.799 0.0565 0.935 0.771
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.985 0.000 1.000
#> GSM907859 2 0.3431 0.938 0.064 0.936
#> GSM907860 2 0.0000 0.985 0.000 1.000
#> GSM907854 2 0.0000 0.985 0.000 1.000
#> GSM907855 2 0.0000 0.985 0.000 1.000
#> GSM907856 2 0.0000 0.985 0.000 1.000
#> GSM907857 2 0.0000 0.985 0.000 1.000
#> GSM907825 2 0.0938 0.978 0.012 0.988
#> GSM907828 2 0.0000 0.985 0.000 1.000
#> GSM907832 2 0.0000 0.985 0.000 1.000
#> GSM907833 2 0.0000 0.985 0.000 1.000
#> GSM907834 2 0.0000 0.985 0.000 1.000
#> GSM907826 2 0.0000 0.985 0.000 1.000
#> GSM907827 2 0.0000 0.985 0.000 1.000
#> GSM907829 2 0.3584 0.930 0.068 0.932
#> GSM907830 2 0.0000 0.985 0.000 1.000
#> GSM907831 2 0.0000 0.985 0.000 1.000
#> GSM907792 1 0.0000 0.995 1.000 0.000
#> GSM907795 1 0.0000 0.995 1.000 0.000
#> GSM907801 1 0.0000 0.995 1.000 0.000
#> GSM907802 1 0.0000 0.995 1.000 0.000
#> GSM907804 1 0.0000 0.995 1.000 0.000
#> GSM907805 1 0.0000 0.995 1.000 0.000
#> GSM907806 1 0.0000 0.995 1.000 0.000
#> GSM907793 1 0.0000 0.995 1.000 0.000
#> GSM907794 1 0.0000 0.995 1.000 0.000
#> GSM907796 1 0.0000 0.995 1.000 0.000
#> GSM907797 1 0.0000 0.995 1.000 0.000
#> GSM907798 1 0.0000 0.995 1.000 0.000
#> GSM907799 1 0.0000 0.995 1.000 0.000
#> GSM907800 1 0.0000 0.995 1.000 0.000
#> GSM907803 1 0.0000 0.995 1.000 0.000
#> GSM907864 2 0.3431 0.938 0.064 0.936
#> GSM907865 2 0.4431 0.911 0.092 0.908
#> GSM907868 2 0.0000 0.985 0.000 1.000
#> GSM907869 2 0.5059 0.889 0.112 0.888
#> GSM907870 2 0.0000 0.985 0.000 1.000
#> GSM907861 2 0.0000 0.985 0.000 1.000
#> GSM907862 2 0.0000 0.985 0.000 1.000
#> GSM907863 2 0.0000 0.985 0.000 1.000
#> GSM907866 2 0.0000 0.985 0.000 1.000
#> GSM907867 2 0.0000 0.985 0.000 1.000
#> GSM907839 2 0.2423 0.958 0.040 0.960
#> GSM907840 2 0.0672 0.980 0.008 0.992
#> GSM907842 2 0.0000 0.985 0.000 1.000
#> GSM907843 2 0.0000 0.985 0.000 1.000
#> GSM907845 2 0.6531 0.819 0.168 0.832
#> GSM907846 2 0.2603 0.955 0.044 0.956
#> GSM907848 2 0.0000 0.985 0.000 1.000
#> GSM907851 2 0.0938 0.978 0.012 0.988
#> GSM907835 2 0.0000 0.985 0.000 1.000
#> GSM907836 2 0.0000 0.985 0.000 1.000
#> GSM907837 2 0.0000 0.985 0.000 1.000
#> GSM907838 2 0.0000 0.985 0.000 1.000
#> GSM907841 2 0.0000 0.985 0.000 1.000
#> GSM907844 2 0.0000 0.985 0.000 1.000
#> GSM907847 2 0.0000 0.985 0.000 1.000
#> GSM907849 2 0.0672 0.980 0.008 0.992
#> GSM907850 2 0.0000 0.985 0.000 1.000
#> GSM907852 2 0.0376 0.983 0.004 0.996
#> GSM907853 2 0.0672 0.980 0.008 0.992
#> GSM907807 1 0.0000 0.995 1.000 0.000
#> GSM907813 1 0.0000 0.995 1.000 0.000
#> GSM907814 1 0.0000 0.995 1.000 0.000
#> GSM907816 1 0.0000 0.995 1.000 0.000
#> GSM907818 1 0.0000 0.995 1.000 0.000
#> GSM907819 1 0.0000 0.995 1.000 0.000
#> GSM907820 1 0.0000 0.995 1.000 0.000
#> GSM907822 1 0.0000 0.995 1.000 0.000
#> GSM907823 1 0.0000 0.995 1.000 0.000
#> GSM907808 1 0.0000 0.995 1.000 0.000
#> GSM907809 1 0.0000 0.995 1.000 0.000
#> GSM907810 1 0.0000 0.995 1.000 0.000
#> GSM907811 1 0.0000 0.995 1.000 0.000
#> GSM907812 1 0.0000 0.995 1.000 0.000
#> GSM907815 1 0.0672 0.988 0.992 0.008
#> GSM907817 1 0.0376 0.991 0.996 0.004
#> GSM907821 1 0.3584 0.929 0.932 0.068
#> GSM907824 1 0.4431 0.903 0.908 0.092
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.5560 0.690 0.000 0.300 0.700
#> GSM907859 3 0.0747 0.713 0.000 0.016 0.984
#> GSM907860 2 0.6280 -0.138 0.000 0.540 0.460
#> GSM907854 2 0.5835 0.363 0.000 0.660 0.340
#> GSM907855 3 0.5968 0.602 0.000 0.364 0.636
#> GSM907856 3 0.5178 0.719 0.000 0.256 0.744
#> GSM907857 3 0.5363 0.707 0.000 0.276 0.724
#> GSM907825 2 0.0747 0.862 0.016 0.984 0.000
#> GSM907828 2 0.0237 0.870 0.000 0.996 0.004
#> GSM907832 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907834 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907826 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907827 2 0.0237 0.870 0.000 0.996 0.004
#> GSM907829 2 0.3845 0.722 0.116 0.872 0.012
#> GSM907830 2 0.3816 0.739 0.000 0.852 0.148
#> GSM907831 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907792 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907795 1 0.0424 0.944 0.992 0.000 0.008
#> GSM907801 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907802 1 0.2796 0.872 0.908 0.092 0.000
#> GSM907804 1 0.1411 0.927 0.964 0.000 0.036
#> GSM907805 1 0.0747 0.940 0.984 0.000 0.016
#> GSM907806 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907793 1 0.0237 0.945 0.996 0.000 0.004
#> GSM907794 1 0.0747 0.938 0.984 0.016 0.000
#> GSM907796 1 0.0592 0.942 0.988 0.000 0.012
#> GSM907797 1 0.2711 0.884 0.912 0.000 0.088
#> GSM907798 1 0.0592 0.942 0.988 0.000 0.012
#> GSM907799 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907800 1 0.0592 0.941 0.988 0.012 0.000
#> GSM907803 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907864 3 0.3267 0.712 0.000 0.116 0.884
#> GSM907865 3 0.0592 0.711 0.000 0.012 0.988
#> GSM907868 3 0.6235 0.451 0.000 0.436 0.564
#> GSM907869 3 0.0237 0.708 0.000 0.004 0.996
#> GSM907870 2 0.0424 0.868 0.000 0.992 0.008
#> GSM907861 2 0.4887 0.613 0.000 0.772 0.228
#> GSM907862 2 0.5431 0.501 0.000 0.716 0.284
#> GSM907863 2 0.5058 0.583 0.000 0.756 0.244
#> GSM907866 3 0.5327 0.709 0.000 0.272 0.728
#> GSM907867 2 0.5529 0.466 0.000 0.704 0.296
#> GSM907839 2 0.6215 0.209 0.000 0.572 0.428
#> GSM907840 3 0.3879 0.693 0.000 0.152 0.848
#> GSM907842 2 0.4235 0.721 0.000 0.824 0.176
#> GSM907843 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907845 2 0.4861 0.616 0.180 0.808 0.012
#> GSM907846 2 0.1964 0.838 0.000 0.944 0.056
#> GSM907848 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907851 2 0.0424 0.867 0.008 0.992 0.000
#> GSM907835 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907836 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907837 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907838 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907841 3 0.6215 0.471 0.000 0.428 0.572
#> GSM907844 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.871 0.000 1.000 0.000
#> GSM907849 2 0.0592 0.865 0.012 0.988 0.000
#> GSM907850 2 0.0237 0.870 0.004 0.996 0.000
#> GSM907852 2 0.0747 0.862 0.016 0.984 0.000
#> GSM907853 2 0.0892 0.858 0.020 0.980 0.000
#> GSM907807 1 0.0237 0.945 0.996 0.000 0.004
#> GSM907813 1 0.5733 0.593 0.676 0.000 0.324
#> GSM907814 1 0.6267 0.343 0.548 0.000 0.452
#> GSM907816 1 0.0237 0.945 0.996 0.000 0.004
#> GSM907818 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907820 1 0.4702 0.718 0.788 0.212 0.000
#> GSM907822 1 0.0424 0.944 0.992 0.000 0.008
#> GSM907823 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.946 1.000 0.000 0.000
#> GSM907815 3 0.5497 0.423 0.292 0.000 0.708
#> GSM907817 1 0.1289 0.926 0.968 0.032 0.000
#> GSM907821 1 0.3193 0.862 0.896 0.100 0.004
#> GSM907824 1 0.3752 0.813 0.856 0.144 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.6587 0.32176 0.000 0.100 0.576 0.324
#> GSM907859 4 0.0707 0.52165 0.000 0.000 0.020 0.980
#> GSM907860 2 0.7169 0.11552 0.000 0.508 0.148 0.344
#> GSM907854 3 0.1545 0.57866 0.000 0.040 0.952 0.008
#> GSM907855 4 0.7216 -0.09548 0.000 0.140 0.412 0.448
#> GSM907856 4 0.5848 0.14822 0.000 0.040 0.376 0.584
#> GSM907857 3 0.0779 0.55535 0.000 0.004 0.980 0.016
#> GSM907825 2 0.1396 0.86732 0.004 0.960 0.032 0.004
#> GSM907828 2 0.0657 0.88227 0.000 0.984 0.004 0.012
#> GSM907832 2 0.0188 0.88389 0.000 0.996 0.004 0.000
#> GSM907833 2 0.0336 0.88367 0.000 0.992 0.000 0.008
#> GSM907834 2 0.0895 0.87771 0.000 0.976 0.020 0.004
#> GSM907826 2 0.0524 0.88232 0.000 0.988 0.008 0.004
#> GSM907827 2 0.0804 0.88132 0.000 0.980 0.008 0.012
#> GSM907829 3 0.4222 0.53424 0.080 0.084 0.832 0.004
#> GSM907830 2 0.3224 0.79681 0.000 0.864 0.016 0.120
#> GSM907831 2 0.0657 0.88106 0.000 0.984 0.012 0.004
#> GSM907792 1 0.0188 0.93449 0.996 0.000 0.000 0.004
#> GSM907795 1 0.1022 0.92614 0.968 0.000 0.000 0.032
#> GSM907801 1 0.0779 0.93318 0.980 0.004 0.000 0.016
#> GSM907802 1 0.1674 0.91771 0.952 0.032 0.012 0.004
#> GSM907804 1 0.3074 0.80531 0.848 0.000 0.000 0.152
#> GSM907805 1 0.1716 0.90442 0.936 0.000 0.000 0.064
#> GSM907806 1 0.1042 0.93295 0.972 0.008 0.000 0.020
#> GSM907793 1 0.0000 0.93421 1.000 0.000 0.000 0.000
#> GSM907794 1 0.0844 0.93241 0.980 0.012 0.004 0.004
#> GSM907796 1 0.1489 0.92117 0.952 0.000 0.044 0.004
#> GSM907797 1 0.4999 0.10145 0.508 0.000 0.492 0.000
#> GSM907798 1 0.1824 0.91075 0.936 0.000 0.060 0.004
#> GSM907799 1 0.0188 0.93454 0.996 0.004 0.000 0.000
#> GSM907800 1 0.1082 0.92985 0.972 0.020 0.004 0.004
#> GSM907803 1 0.0336 0.93438 0.992 0.008 0.000 0.000
#> GSM907864 4 0.0592 0.52080 0.000 0.016 0.000 0.984
#> GSM907865 4 0.0895 0.52145 0.000 0.004 0.020 0.976
#> GSM907868 3 0.4969 0.54833 0.000 0.140 0.772 0.088
#> GSM907869 4 0.4585 0.26269 0.000 0.000 0.332 0.668
#> GSM907870 2 0.0592 0.88152 0.000 0.984 0.000 0.016
#> GSM907861 3 0.5024 0.38726 0.000 0.360 0.632 0.008
#> GSM907862 2 0.5798 0.55758 0.000 0.696 0.096 0.208
#> GSM907863 2 0.4731 0.68756 0.000 0.780 0.060 0.160
#> GSM907866 3 0.4820 0.34403 0.000 0.012 0.692 0.296
#> GSM907867 2 0.7188 0.12275 0.000 0.528 0.308 0.164
#> GSM907839 2 0.4994 0.24489 0.000 0.520 0.000 0.480
#> GSM907840 4 0.0817 0.51623 0.000 0.024 0.000 0.976
#> GSM907842 2 0.4431 0.58631 0.000 0.696 0.000 0.304
#> GSM907843 2 0.0524 0.88292 0.000 0.988 0.004 0.008
#> GSM907845 3 0.7380 0.34122 0.184 0.276 0.536 0.004
#> GSM907846 2 0.3982 0.68977 0.000 0.776 0.004 0.220
#> GSM907848 2 0.0188 0.88312 0.000 0.996 0.004 0.000
#> GSM907851 2 0.0844 0.87729 0.012 0.980 0.004 0.004
#> GSM907835 2 0.0188 0.88389 0.000 0.996 0.004 0.000
#> GSM907836 2 0.0524 0.88328 0.000 0.988 0.004 0.008
#> GSM907837 2 0.0188 0.88400 0.000 0.996 0.000 0.004
#> GSM907838 2 0.0336 0.88375 0.000 0.992 0.000 0.008
#> GSM907841 4 0.7227 -0.00169 0.000 0.148 0.368 0.484
#> GSM907844 2 0.0336 0.88337 0.000 0.992 0.008 0.000
#> GSM907847 2 0.0188 0.88312 0.000 0.996 0.004 0.000
#> GSM907849 2 0.0712 0.88129 0.008 0.984 0.004 0.004
#> GSM907850 2 0.0188 0.88389 0.000 0.996 0.004 0.000
#> GSM907852 2 0.0376 0.88216 0.004 0.992 0.000 0.004
#> GSM907853 2 0.1396 0.86002 0.032 0.960 0.004 0.004
#> GSM907807 1 0.0817 0.92984 0.976 0.000 0.000 0.024
#> GSM907813 4 0.4999 -0.10300 0.492 0.000 0.000 0.508
#> GSM907814 4 0.4585 0.28331 0.332 0.000 0.000 0.668
#> GSM907816 1 0.1543 0.92516 0.956 0.008 0.004 0.032
#> GSM907818 1 0.0844 0.93241 0.980 0.012 0.004 0.004
#> GSM907819 1 0.0672 0.93429 0.984 0.000 0.008 0.008
#> GSM907820 1 0.3289 0.82253 0.864 0.120 0.004 0.012
#> GSM907822 1 0.1675 0.91675 0.948 0.004 0.004 0.044
#> GSM907823 1 0.1543 0.92516 0.956 0.008 0.004 0.032
#> GSM907808 1 0.0188 0.93433 0.996 0.000 0.004 0.000
#> GSM907809 1 0.0188 0.93433 0.996 0.000 0.004 0.000
#> GSM907810 1 0.0188 0.93454 0.996 0.004 0.000 0.000
#> GSM907811 1 0.0336 0.93438 0.992 0.008 0.000 0.000
#> GSM907812 1 0.0921 0.92822 0.972 0.000 0.028 0.000
#> GSM907815 3 0.6336 0.21774 0.088 0.000 0.608 0.304
#> GSM907817 1 0.1004 0.92805 0.972 0.024 0.000 0.004
#> GSM907821 1 0.5076 0.63068 0.712 0.024 0.260 0.004
#> GSM907824 1 0.3016 0.88023 0.896 0.040 0.060 0.004
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.3301 0.7300 0.000 0.036 0.864 0.076 0.024
#> GSM907859 4 0.1357 0.6883 0.000 0.000 0.048 0.948 0.004
#> GSM907860 3 0.3909 0.7626 0.000 0.216 0.760 0.024 0.000
#> GSM907854 3 0.2172 0.7190 0.000 0.020 0.916 0.004 0.060
#> GSM907855 3 0.3346 0.7634 0.000 0.092 0.844 0.064 0.000
#> GSM907856 3 0.3489 0.6476 0.000 0.004 0.784 0.208 0.004
#> GSM907857 3 0.3280 0.5885 0.000 0.000 0.812 0.012 0.176
#> GSM907825 2 0.2124 0.8424 0.000 0.900 0.004 0.000 0.096
#> GSM907828 2 0.1331 0.8579 0.000 0.952 0.040 0.008 0.000
#> GSM907832 2 0.2533 0.8353 0.000 0.888 0.008 0.008 0.096
#> GSM907833 2 0.2964 0.8061 0.000 0.856 0.000 0.024 0.120
#> GSM907834 2 0.2971 0.7911 0.000 0.836 0.008 0.000 0.156
#> GSM907826 2 0.1831 0.8373 0.000 0.920 0.076 0.004 0.000
#> GSM907827 2 0.2471 0.7746 0.000 0.864 0.136 0.000 0.000
#> GSM907829 5 0.5743 0.4157 0.016 0.164 0.156 0.000 0.664
#> GSM907830 2 0.3658 0.7835 0.000 0.832 0.016 0.116 0.036
#> GSM907831 2 0.1469 0.8657 0.000 0.948 0.016 0.000 0.036
#> GSM907792 1 0.0510 0.9138 0.984 0.000 0.000 0.000 0.016
#> GSM907795 1 0.0963 0.9093 0.964 0.000 0.000 0.000 0.036
#> GSM907801 1 0.1121 0.9064 0.956 0.000 0.000 0.000 0.044
#> GSM907802 1 0.5024 0.7768 0.764 0.052 0.040 0.012 0.132
#> GSM907804 1 0.3323 0.8368 0.844 0.000 0.000 0.056 0.100
#> GSM907805 1 0.3485 0.8207 0.828 0.000 0.000 0.124 0.048
#> GSM907806 1 0.0671 0.9148 0.980 0.004 0.000 0.000 0.016
#> GSM907793 1 0.0510 0.9137 0.984 0.000 0.000 0.000 0.016
#> GSM907794 1 0.0404 0.9153 0.988 0.000 0.000 0.000 0.012
#> GSM907796 1 0.1357 0.9080 0.948 0.000 0.004 0.000 0.048
#> GSM907797 5 0.5260 0.2873 0.204 0.000 0.108 0.004 0.684
#> GSM907798 1 0.1697 0.9029 0.932 0.000 0.008 0.000 0.060
#> GSM907799 1 0.0510 0.9137 0.984 0.000 0.000 0.000 0.016
#> GSM907800 1 0.2597 0.8899 0.904 0.016 0.012 0.008 0.060
#> GSM907803 1 0.0290 0.9157 0.992 0.000 0.000 0.000 0.008
#> GSM907864 4 0.2644 0.6799 0.000 0.020 0.068 0.896 0.016
#> GSM907865 4 0.0794 0.6853 0.000 0.000 0.028 0.972 0.000
#> GSM907868 3 0.2104 0.7497 0.000 0.044 0.924 0.024 0.008
#> GSM907869 4 0.4836 0.4037 0.000 0.000 0.304 0.652 0.044
#> GSM907870 3 0.4774 0.6350 0.000 0.308 0.660 0.012 0.020
#> GSM907861 3 0.3496 0.7632 0.000 0.200 0.788 0.000 0.012
#> GSM907862 3 0.3809 0.7258 0.000 0.256 0.736 0.000 0.008
#> GSM907863 3 0.3910 0.7368 0.000 0.248 0.740 0.008 0.004
#> GSM907866 3 0.4049 0.6307 0.000 0.000 0.780 0.164 0.056
#> GSM907867 3 0.3659 0.7592 0.000 0.220 0.768 0.012 0.000
#> GSM907839 2 0.6122 0.2584 0.004 0.528 0.008 0.368 0.092
#> GSM907840 4 0.2130 0.6423 0.000 0.080 0.012 0.908 0.000
#> GSM907842 2 0.3696 0.7010 0.000 0.772 0.000 0.212 0.016
#> GSM907843 2 0.0960 0.8647 0.000 0.972 0.016 0.008 0.004
#> GSM907845 5 0.6117 0.0385 0.012 0.428 0.088 0.000 0.472
#> GSM907846 2 0.5331 0.6198 0.008 0.720 0.012 0.140 0.120
#> GSM907848 2 0.1764 0.8501 0.000 0.928 0.000 0.008 0.064
#> GSM907851 2 0.2151 0.8485 0.020 0.924 0.016 0.000 0.040
#> GSM907835 2 0.0566 0.8657 0.000 0.984 0.004 0.000 0.012
#> GSM907836 2 0.1671 0.8367 0.000 0.924 0.076 0.000 0.000
#> GSM907837 2 0.3067 0.7609 0.000 0.844 0.140 0.012 0.004
#> GSM907838 2 0.2733 0.7956 0.000 0.872 0.112 0.012 0.004
#> GSM907841 4 0.6419 0.4112 0.000 0.140 0.148 0.640 0.072
#> GSM907844 2 0.0579 0.8658 0.000 0.984 0.008 0.000 0.008
#> GSM907847 2 0.0613 0.8654 0.000 0.984 0.004 0.008 0.004
#> GSM907849 2 0.1130 0.8652 0.012 0.968 0.012 0.004 0.004
#> GSM907850 2 0.0613 0.8657 0.000 0.984 0.004 0.004 0.008
#> GSM907852 2 0.0807 0.8632 0.000 0.976 0.012 0.012 0.000
#> GSM907853 2 0.3093 0.8096 0.016 0.856 0.004 0.004 0.120
#> GSM907807 1 0.0510 0.9138 0.984 0.000 0.000 0.000 0.016
#> GSM907813 4 0.5422 0.2987 0.296 0.000 0.000 0.616 0.088
#> GSM907814 4 0.3002 0.5999 0.116 0.000 0.000 0.856 0.028
#> GSM907816 1 0.1270 0.9033 0.948 0.000 0.000 0.000 0.052
#> GSM907818 1 0.2179 0.8797 0.888 0.000 0.000 0.000 0.112
#> GSM907819 1 0.3002 0.8505 0.856 0.000 0.000 0.028 0.116
#> GSM907820 1 0.6827 0.3871 0.576 0.240 0.032 0.012 0.140
#> GSM907822 1 0.0794 0.9120 0.972 0.000 0.000 0.000 0.028
#> GSM907823 1 0.1608 0.8939 0.928 0.000 0.000 0.000 0.072
#> GSM907808 1 0.0000 0.9150 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9150 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.9150 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.1460 0.9100 0.956 0.004 0.012 0.008 0.020
#> GSM907812 1 0.1251 0.9101 0.956 0.000 0.008 0.000 0.036
#> GSM907815 5 0.6608 -0.1461 0.012 0.000 0.152 0.372 0.464
#> GSM907817 1 0.2822 0.8829 0.896 0.016 0.024 0.008 0.056
#> GSM907821 1 0.4680 0.7572 0.760 0.036 0.028 0.004 0.172
#> GSM907824 1 0.4658 0.8003 0.792 0.032 0.056 0.012 0.108
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.2053 0.747 0.000 0.024 0.916 0.004 0.004 0.052
#> GSM907859 4 0.4060 0.647 0.000 0.000 0.120 0.764 0.004 0.112
#> GSM907860 3 0.3748 0.813 0.000 0.224 0.748 0.000 0.012 0.016
#> GSM907854 3 0.1605 0.778 0.000 0.044 0.936 0.000 0.004 0.016
#> GSM907855 3 0.3296 0.818 0.000 0.188 0.792 0.000 0.008 0.012
#> GSM907856 3 0.3792 0.712 0.000 0.032 0.788 0.160 0.004 0.016
#> GSM907857 3 0.2060 0.671 0.000 0.000 0.900 0.000 0.016 0.084
#> GSM907825 2 0.1984 0.801 0.000 0.912 0.000 0.000 0.056 0.032
#> GSM907828 2 0.1003 0.797 0.000 0.964 0.028 0.000 0.004 0.004
#> GSM907832 2 0.2509 0.788 0.000 0.876 0.000 0.000 0.036 0.088
#> GSM907833 2 0.4357 0.706 0.000 0.744 0.000 0.020 0.168 0.068
#> GSM907834 2 0.5543 0.334 0.000 0.488 0.000 0.000 0.372 0.140
#> GSM907826 2 0.1493 0.787 0.004 0.936 0.056 0.000 0.004 0.000
#> GSM907827 2 0.2432 0.772 0.000 0.888 0.080 0.000 0.024 0.008
#> GSM907829 2 0.7307 0.315 0.016 0.480 0.176 0.000 0.128 0.200
#> GSM907830 2 0.6281 0.470 0.000 0.548 0.012 0.204 0.212 0.024
#> GSM907831 2 0.2502 0.795 0.000 0.884 0.012 0.000 0.084 0.020
#> GSM907792 1 0.0260 0.822 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907795 1 0.1176 0.806 0.956 0.000 0.000 0.000 0.020 0.024
#> GSM907801 1 0.0909 0.818 0.968 0.000 0.000 0.000 0.012 0.020
#> GSM907802 5 0.5294 0.623 0.320 0.040 0.008 0.000 0.600 0.032
#> GSM907804 5 0.7006 0.395 0.344 0.000 0.008 0.060 0.400 0.188
#> GSM907805 1 0.5617 0.440 0.648 0.004 0.000 0.072 0.072 0.204
#> GSM907806 1 0.4053 0.206 0.628 0.004 0.000 0.004 0.360 0.004
#> GSM907793 1 0.0508 0.823 0.984 0.000 0.000 0.004 0.012 0.000
#> GSM907794 1 0.0790 0.818 0.968 0.000 0.000 0.000 0.032 0.000
#> GSM907796 1 0.0862 0.821 0.972 0.000 0.004 0.000 0.008 0.016
#> GSM907797 6 0.7226 0.000 0.140 0.000 0.064 0.048 0.256 0.492
#> GSM907798 1 0.1225 0.813 0.952 0.000 0.000 0.000 0.036 0.012
#> GSM907799 1 0.1082 0.815 0.956 0.000 0.000 0.004 0.040 0.000
#> GSM907800 5 0.3969 0.643 0.276 0.012 0.012 0.000 0.700 0.000
#> GSM907803 1 0.1141 0.808 0.948 0.000 0.000 0.000 0.052 0.000
#> GSM907864 4 0.2699 0.708 0.000 0.040 0.028 0.884 0.000 0.048
#> GSM907865 4 0.0603 0.709 0.000 0.004 0.016 0.980 0.000 0.000
#> GSM907868 3 0.2022 0.779 0.000 0.052 0.916 0.000 0.008 0.024
#> GSM907869 4 0.4294 0.539 0.000 0.000 0.248 0.692 0.000 0.060
#> GSM907870 3 0.5082 0.714 0.000 0.296 0.624 0.000 0.048 0.032
#> GSM907861 3 0.3485 0.821 0.000 0.204 0.772 0.000 0.004 0.020
#> GSM907862 3 0.4029 0.807 0.000 0.228 0.732 0.000 0.020 0.020
#> GSM907863 3 0.4029 0.807 0.000 0.228 0.732 0.000 0.020 0.020
#> GSM907866 3 0.3012 0.735 0.000 0.032 0.872 0.056 0.008 0.032
#> GSM907867 3 0.3693 0.816 0.000 0.216 0.756 0.000 0.012 0.016
#> GSM907839 2 0.4775 0.604 0.000 0.668 0.004 0.232 0.000 0.096
#> GSM907840 4 0.1151 0.715 0.000 0.032 0.000 0.956 0.000 0.012
#> GSM907842 2 0.4900 0.590 0.000 0.656 0.000 0.232 0.004 0.108
#> GSM907843 2 0.0777 0.798 0.000 0.972 0.024 0.000 0.000 0.004
#> GSM907845 2 0.5465 0.594 0.000 0.624 0.036 0.000 0.248 0.092
#> GSM907846 2 0.5851 0.505 0.000 0.568 0.000 0.088 0.052 0.292
#> GSM907848 2 0.3134 0.747 0.000 0.808 0.000 0.000 0.168 0.024
#> GSM907851 2 0.3424 0.761 0.008 0.836 0.016 0.000 0.040 0.100
#> GSM907835 2 0.0777 0.805 0.000 0.972 0.004 0.000 0.024 0.000
#> GSM907836 2 0.1411 0.785 0.000 0.936 0.060 0.000 0.004 0.000
#> GSM907837 2 0.4209 0.664 0.000 0.744 0.052 0.000 0.188 0.016
#> GSM907838 2 0.4322 0.673 0.000 0.744 0.084 0.000 0.160 0.012
#> GSM907841 4 0.6234 0.323 0.000 0.260 0.092 0.564 0.004 0.080
#> GSM907844 2 0.1606 0.805 0.000 0.932 0.008 0.000 0.056 0.004
#> GSM907847 2 0.0692 0.804 0.000 0.976 0.000 0.000 0.020 0.004
#> GSM907849 2 0.1003 0.806 0.004 0.964 0.004 0.000 0.028 0.000
#> GSM907850 2 0.1010 0.806 0.000 0.960 0.004 0.000 0.036 0.000
#> GSM907852 2 0.1858 0.797 0.000 0.904 0.000 0.000 0.092 0.004
#> GSM907853 2 0.3230 0.713 0.000 0.776 0.000 0.000 0.212 0.012
#> GSM907807 1 0.0436 0.821 0.988 0.000 0.000 0.004 0.004 0.004
#> GSM907813 4 0.4063 0.575 0.072 0.000 0.000 0.768 0.012 0.148
#> GSM907814 4 0.1049 0.700 0.032 0.000 0.000 0.960 0.000 0.008
#> GSM907816 1 0.1036 0.820 0.964 0.000 0.000 0.004 0.024 0.008
#> GSM907818 1 0.4238 0.247 0.628 0.000 0.000 0.000 0.344 0.028
#> GSM907819 1 0.5464 0.337 0.584 0.000 0.004 0.016 0.088 0.308
#> GSM907820 5 0.4991 0.462 0.124 0.120 0.004 0.000 0.716 0.036
#> GSM907822 1 0.1116 0.817 0.960 0.000 0.000 0.008 0.028 0.004
#> GSM907823 1 0.2839 0.725 0.860 0.004 0.000 0.000 0.044 0.092
#> GSM907808 1 0.0622 0.817 0.980 0.000 0.000 0.000 0.012 0.008
#> GSM907809 1 0.1168 0.806 0.956 0.000 0.000 0.000 0.016 0.028
#> GSM907810 1 0.0291 0.822 0.992 0.000 0.000 0.004 0.004 0.000
#> GSM907811 1 0.3448 0.409 0.716 0.000 0.004 0.000 0.280 0.000
#> GSM907812 1 0.1699 0.803 0.936 0.000 0.008 0.004 0.040 0.012
#> GSM907815 4 0.5697 0.210 0.000 0.000 0.096 0.524 0.024 0.356
#> GSM907817 5 0.4029 0.676 0.288 0.012 0.012 0.000 0.688 0.000
#> GSM907821 1 0.5169 -0.426 0.468 0.012 0.000 0.000 0.464 0.056
#> GSM907824 5 0.4077 0.617 0.200 0.024 0.016 0.000 0.752 0.008
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
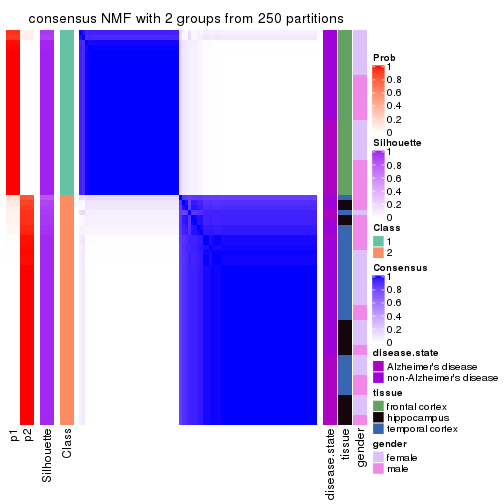
consensus_heatmap(res, k = 3)
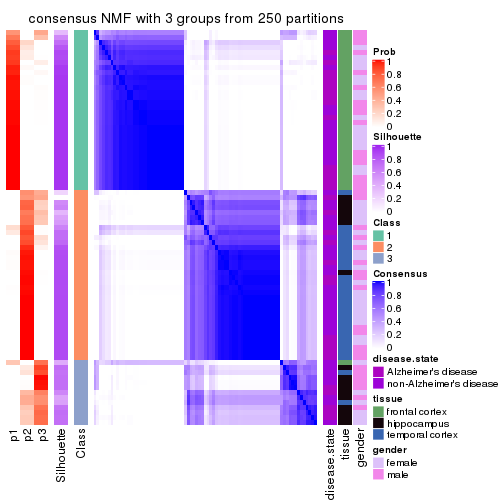
consensus_heatmap(res, k = 4)
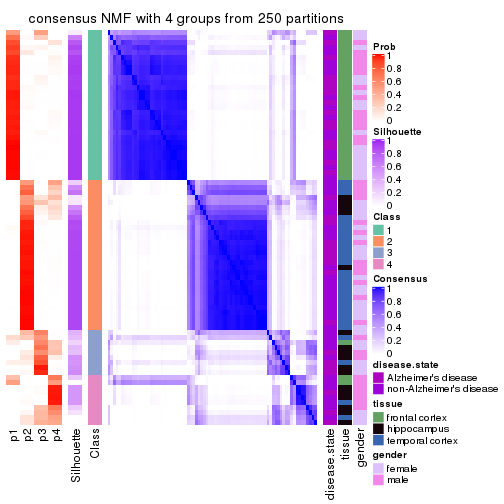
consensus_heatmap(res, k = 5)
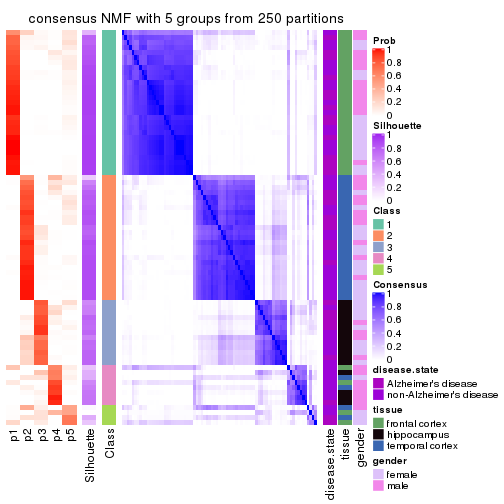
consensus_heatmap(res, k = 6)
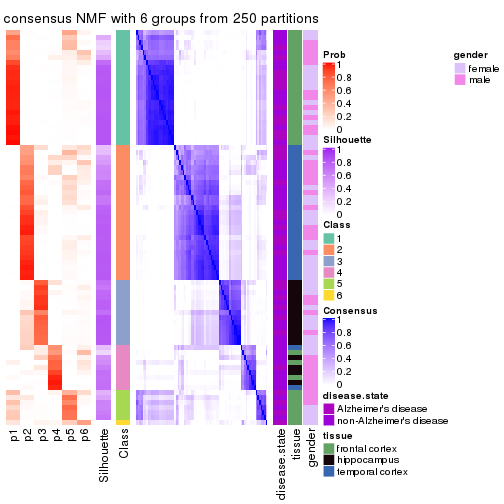
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
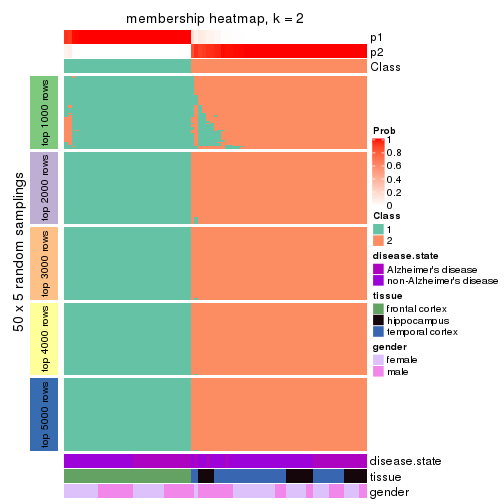
membership_heatmap(res, k = 3)
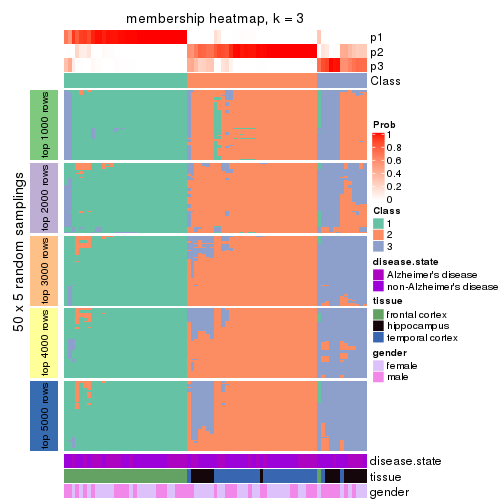
membership_heatmap(res, k = 4)
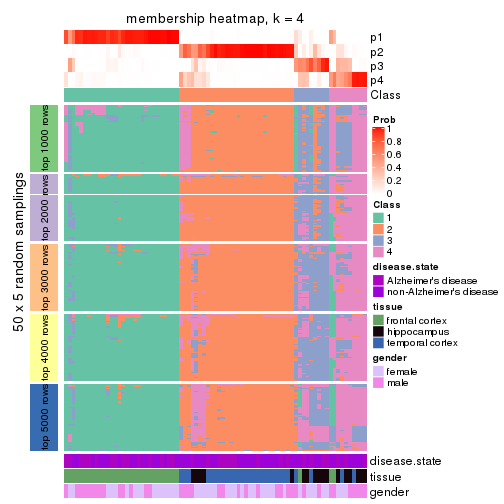
membership_heatmap(res, k = 5)
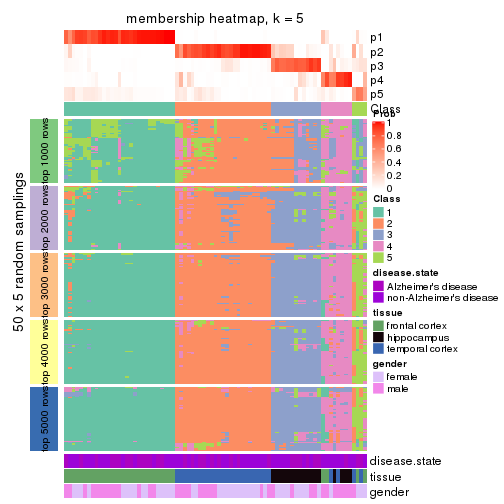
membership_heatmap(res, k = 6)
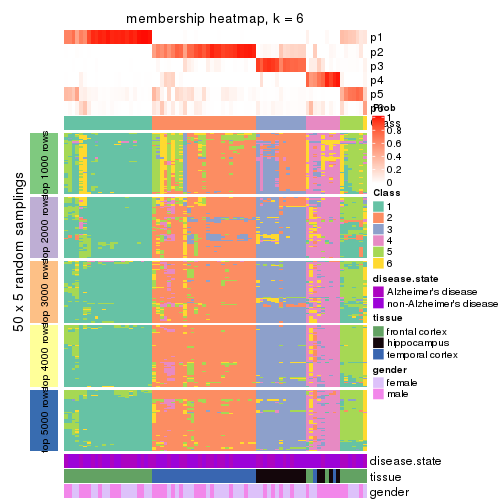
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
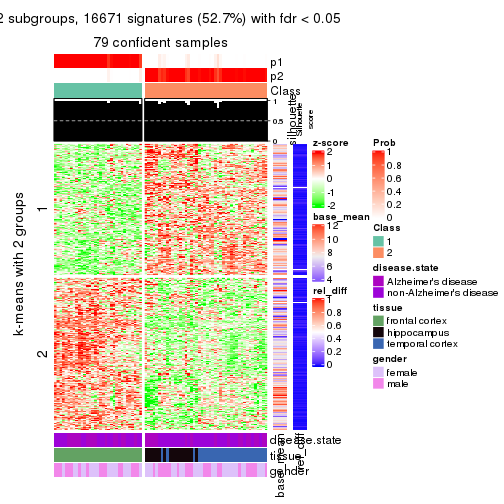
get_signatures(res, k = 3)
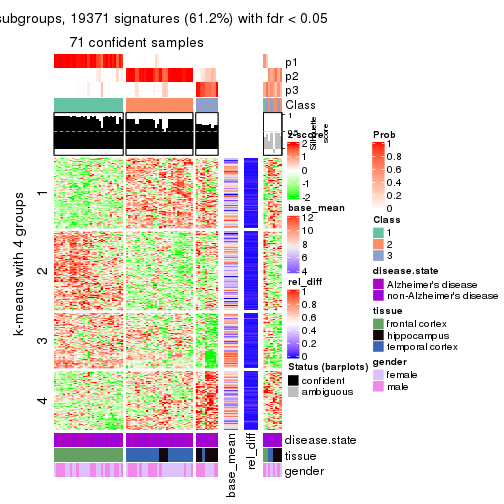
get_signatures(res, k = 4)
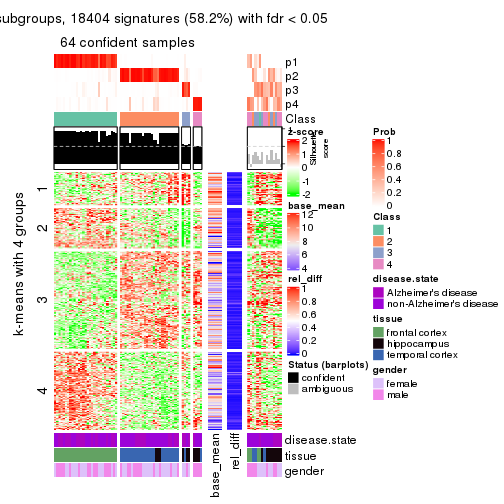
get_signatures(res, k = 5)
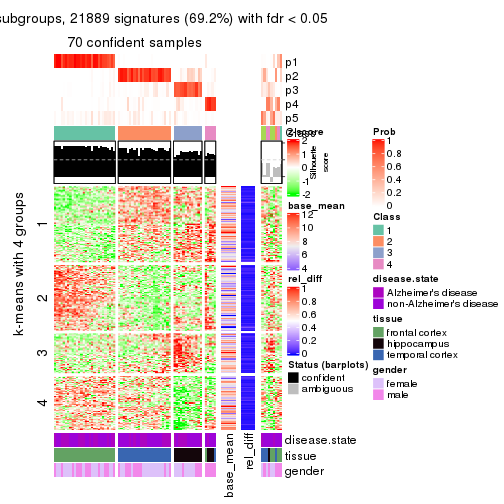
get_signatures(res, k = 6)
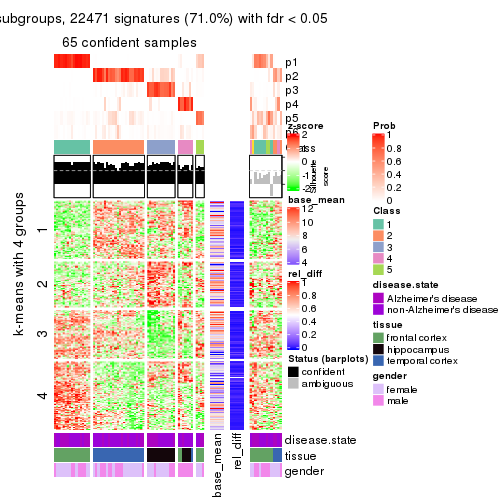
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
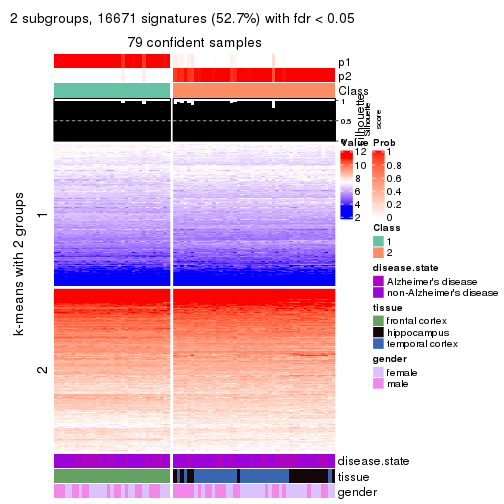
get_signatures(res, k = 3, scale_rows = FALSE)
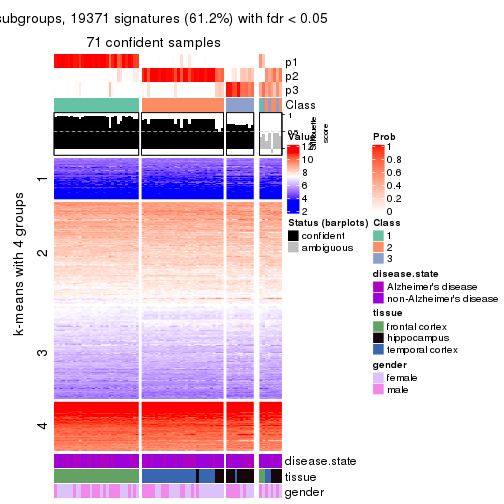
get_signatures(res, k = 4, scale_rows = FALSE)
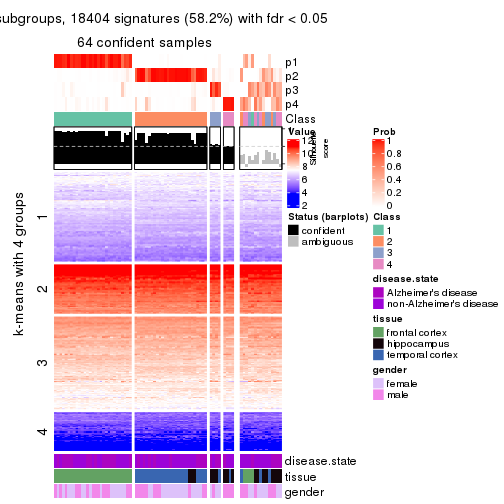
get_signatures(res, k = 5, scale_rows = FALSE)
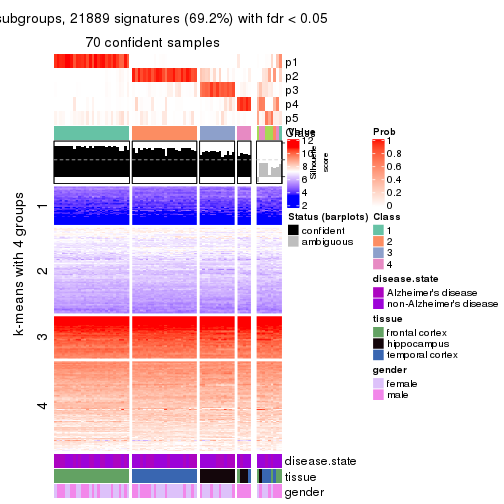
get_signatures(res, k = 6, scale_rows = FALSE)
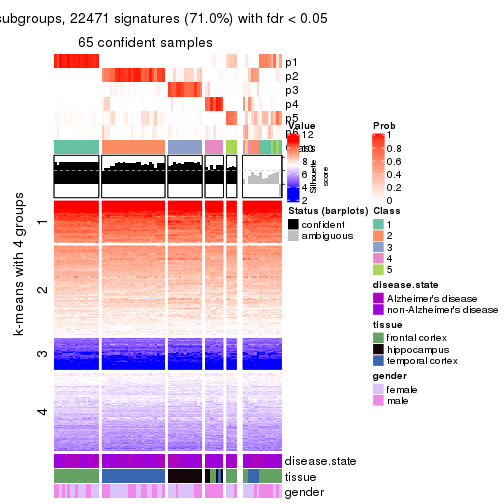
Compare the overlap of signatures from different k:
compare_signatures(res)
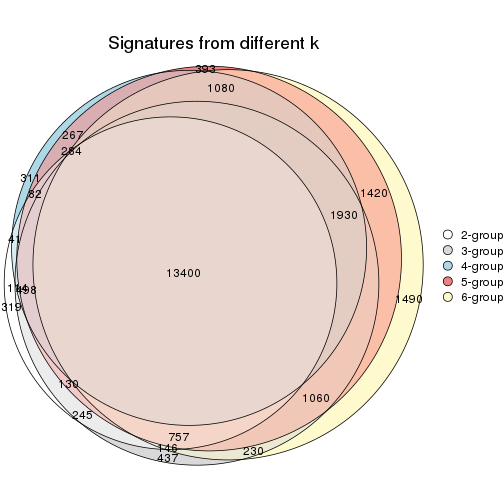
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
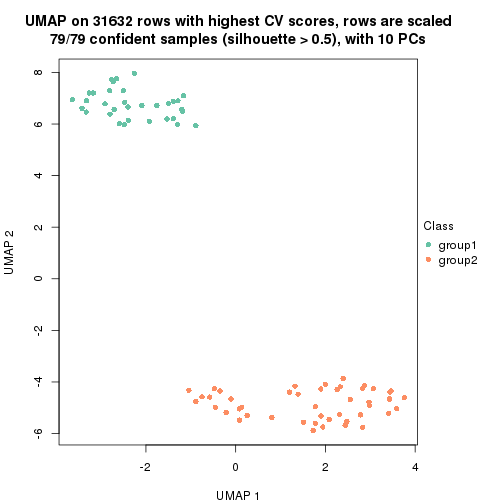
dimension_reduction(res, k = 3, method = "UMAP")
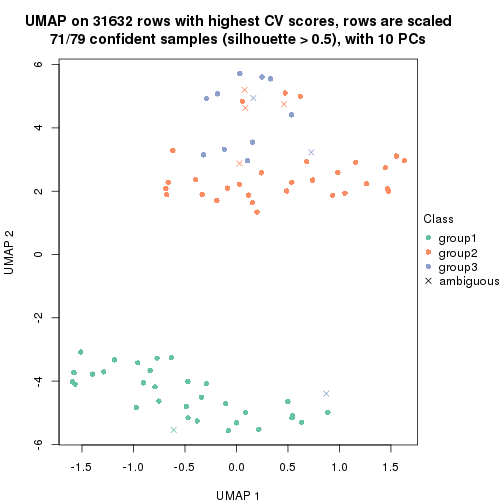
dimension_reduction(res, k = 4, method = "UMAP")
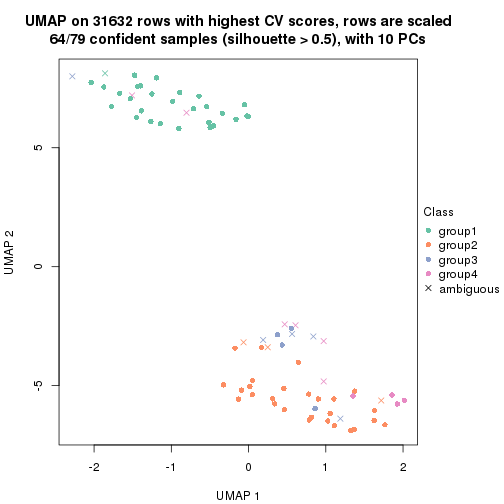
dimension_reduction(res, k = 5, method = "UMAP")
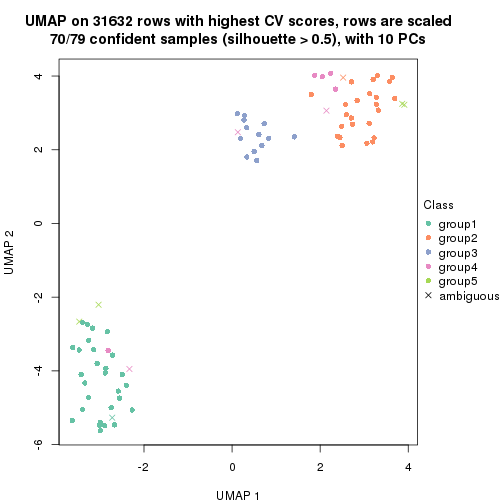
dimension_reduction(res, k = 6, method = "UMAP")
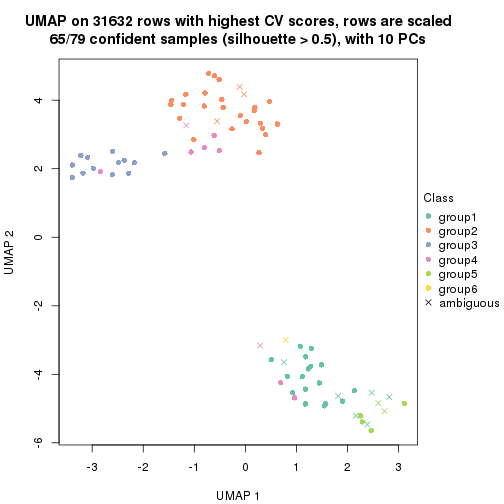
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
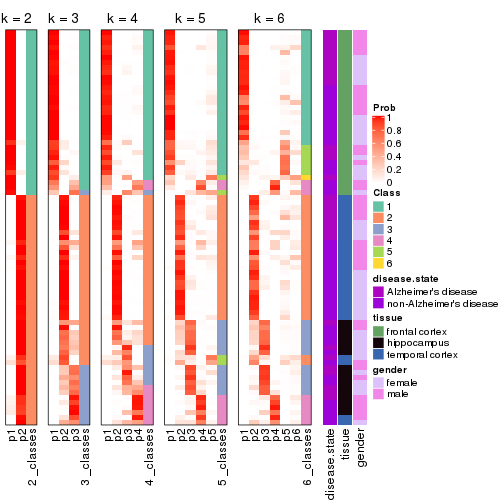
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> CV:NMF 79 0.599 7.00e-18 0.9838 2
#> CV:NMF 71 0.427 3.73e-22 0.5256 3
#> CV:NMF 64 0.313 7.46e-17 0.1254 4
#> CV:NMF 70 0.575 9.71e-26 0.0637 5
#> CV:NMF 65 0.324 1.27e-21 0.0357 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "hclust"]
# you can also extract it by
# res = res_list["MAD:hclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'hclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
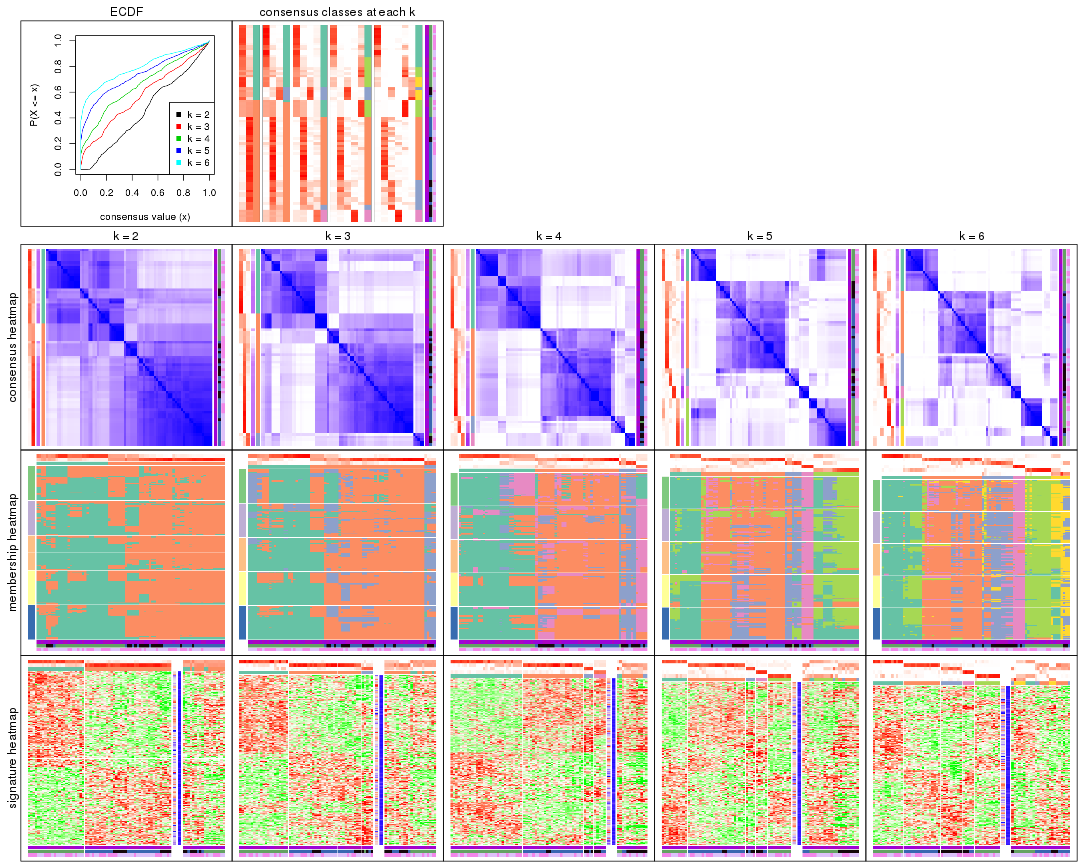
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
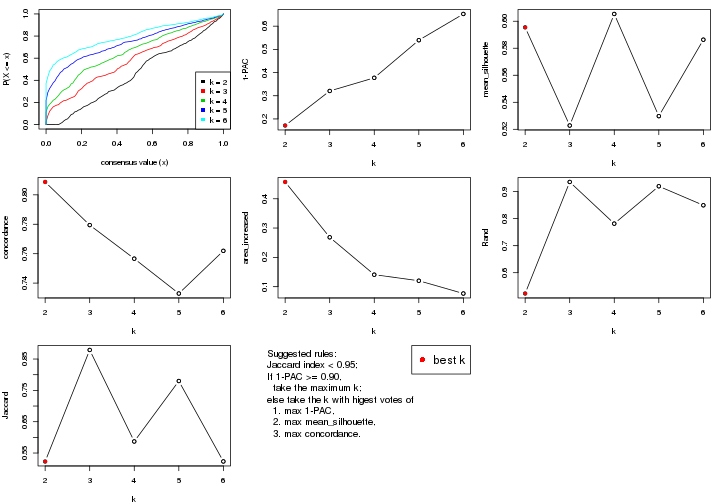
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.172 0.595 0.809 0.4572 0.523 0.523
#> 3 3 0.321 0.523 0.779 0.2684 0.936 0.879
#> 4 4 0.377 0.605 0.757 0.1409 0.782 0.587
#> 5 5 0.539 0.530 0.733 0.1202 0.920 0.780
#> 6 6 0.653 0.586 0.762 0.0766 0.849 0.523
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.7219 0.654 0.200 0.800
#> GSM907859 2 0.9922 0.252 0.448 0.552
#> GSM907860 2 0.2778 0.761 0.048 0.952
#> GSM907854 2 0.7299 0.651 0.204 0.796
#> GSM907855 2 0.5059 0.742 0.112 0.888
#> GSM907856 2 0.5059 0.742 0.112 0.888
#> GSM907857 1 0.9944 0.166 0.544 0.456
#> GSM907825 2 0.0938 0.762 0.012 0.988
#> GSM907828 2 0.5519 0.729 0.128 0.872
#> GSM907832 2 0.3114 0.771 0.056 0.944
#> GSM907833 2 0.2423 0.773 0.040 0.960
#> GSM907834 2 0.0938 0.765 0.012 0.988
#> GSM907826 2 0.1843 0.771 0.028 0.972
#> GSM907827 2 0.1843 0.768 0.028 0.972
#> GSM907829 2 0.4815 0.735 0.104 0.896
#> GSM907830 2 0.4431 0.754 0.092 0.908
#> GSM907831 2 0.1843 0.754 0.028 0.972
#> GSM907792 1 0.6531 0.767 0.832 0.168
#> GSM907795 1 0.4690 0.772 0.900 0.100
#> GSM907801 1 0.4690 0.772 0.900 0.100
#> GSM907802 2 0.9970 -0.182 0.468 0.532
#> GSM907804 2 0.9998 -0.260 0.492 0.508
#> GSM907805 1 0.8713 0.667 0.708 0.292
#> GSM907806 1 0.8499 0.707 0.724 0.276
#> GSM907793 1 0.4939 0.774 0.892 0.108
#> GSM907794 1 0.9954 0.370 0.540 0.460
#> GSM907796 1 0.3274 0.741 0.940 0.060
#> GSM907797 1 0.3879 0.744 0.924 0.076
#> GSM907798 1 0.3274 0.741 0.940 0.060
#> GSM907799 1 0.8207 0.724 0.744 0.256
#> GSM907800 2 0.9983 -0.207 0.476 0.524
#> GSM907803 1 0.8207 0.724 0.744 0.256
#> GSM907864 2 0.9795 0.315 0.416 0.584
#> GSM907865 2 0.9922 0.249 0.448 0.552
#> GSM907868 2 0.6247 0.699 0.156 0.844
#> GSM907869 1 0.9491 0.424 0.632 0.368
#> GSM907870 2 0.5294 0.745 0.120 0.880
#> GSM907861 2 0.6048 0.703 0.148 0.852
#> GSM907862 2 0.3274 0.767 0.060 0.940
#> GSM907863 2 0.3274 0.767 0.060 0.940
#> GSM907866 1 0.9795 0.304 0.584 0.416
#> GSM907867 2 0.2778 0.774 0.048 0.952
#> GSM907839 2 0.9795 0.315 0.416 0.584
#> GSM907840 2 0.9795 0.315 0.416 0.584
#> GSM907842 2 0.8386 0.582 0.268 0.732
#> GSM907843 2 0.5059 0.749 0.112 0.888
#> GSM907845 2 0.7602 0.636 0.220 0.780
#> GSM907846 2 0.3879 0.763 0.076 0.924
#> GSM907848 2 0.2423 0.773 0.040 0.960
#> GSM907851 2 0.5294 0.745 0.120 0.880
#> GSM907835 2 0.1633 0.771 0.024 0.976
#> GSM907836 2 0.1633 0.771 0.024 0.976
#> GSM907837 2 0.2948 0.768 0.052 0.948
#> GSM907838 2 0.2948 0.768 0.052 0.948
#> GSM907841 1 0.9795 0.304 0.584 0.416
#> GSM907844 2 0.2423 0.773 0.040 0.960
#> GSM907847 2 0.2423 0.773 0.040 0.960
#> GSM907849 2 0.4562 0.758 0.096 0.904
#> GSM907850 2 0.2043 0.773 0.032 0.968
#> GSM907852 2 0.1633 0.771 0.024 0.976
#> GSM907853 2 0.2423 0.773 0.040 0.960
#> GSM907807 1 0.4690 0.772 0.900 0.100
#> GSM907813 1 0.4161 0.766 0.916 0.084
#> GSM907814 1 0.4161 0.766 0.916 0.084
#> GSM907816 1 0.5408 0.776 0.876 0.124
#> GSM907818 1 0.9129 0.603 0.672 0.328
#> GSM907819 1 1.0000 0.262 0.504 0.496
#> GSM907820 2 0.9970 -0.182 0.468 0.532
#> GSM907822 1 0.8267 0.721 0.740 0.260
#> GSM907823 1 0.8661 0.679 0.712 0.288
#> GSM907808 1 0.4815 0.774 0.896 0.104
#> GSM907809 1 0.4815 0.774 0.896 0.104
#> GSM907810 1 0.6887 0.761 0.816 0.184
#> GSM907811 1 0.8327 0.717 0.736 0.264
#> GSM907812 1 0.3274 0.741 0.940 0.060
#> GSM907815 1 0.7056 0.638 0.808 0.192
#> GSM907817 2 0.9977 -0.195 0.472 0.528
#> GSM907821 2 0.9970 -0.182 0.468 0.532
#> GSM907824 2 0.9970 -0.182 0.468 0.532
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 2 0.6140 0.1853 0.000 0.596 0.404
#> GSM907859 2 0.9842 0.0486 0.272 0.420 0.308
#> GSM907860 2 0.4840 0.6216 0.016 0.816 0.168
#> GSM907854 2 0.6154 0.1795 0.000 0.592 0.408
#> GSM907855 2 0.5659 0.5468 0.012 0.740 0.248
#> GSM907856 2 0.5659 0.5468 0.012 0.740 0.248
#> GSM907857 3 0.6187 0.7754 0.028 0.248 0.724
#> GSM907825 2 0.2165 0.6745 0.000 0.936 0.064
#> GSM907828 2 0.5965 0.6158 0.108 0.792 0.100
#> GSM907832 2 0.1399 0.6869 0.004 0.968 0.028
#> GSM907833 2 0.0592 0.6891 0.000 0.988 0.012
#> GSM907834 2 0.2165 0.6755 0.000 0.936 0.064
#> GSM907826 2 0.0592 0.6882 0.000 0.988 0.012
#> GSM907827 2 0.2486 0.6804 0.008 0.932 0.060
#> GSM907829 2 0.4233 0.6223 0.004 0.836 0.160
#> GSM907830 2 0.4636 0.6591 0.036 0.848 0.116
#> GSM907831 2 0.2537 0.6700 0.000 0.920 0.080
#> GSM907792 1 0.2356 0.7274 0.928 0.072 0.000
#> GSM907795 1 0.0237 0.7179 0.996 0.004 0.000
#> GSM907801 1 0.0237 0.7179 0.996 0.004 0.000
#> GSM907802 2 0.7665 -0.2078 0.456 0.500 0.044
#> GSM907804 1 0.7586 0.2275 0.480 0.480 0.040
#> GSM907805 1 0.8683 0.5122 0.592 0.236 0.172
#> GSM907806 1 0.4968 0.6912 0.800 0.188 0.012
#> GSM907793 1 0.0829 0.7220 0.984 0.012 0.004
#> GSM907794 1 0.7542 0.3533 0.528 0.432 0.040
#> GSM907796 1 0.6284 0.5037 0.680 0.016 0.304
#> GSM907797 1 0.6497 0.4609 0.648 0.016 0.336
#> GSM907798 1 0.6284 0.5037 0.680 0.016 0.304
#> GSM907799 1 0.4921 0.7054 0.816 0.164 0.020
#> GSM907800 2 0.7671 -0.2284 0.464 0.492 0.044
#> GSM907803 1 0.4921 0.7054 0.816 0.164 0.020
#> GSM907864 2 0.9741 0.0978 0.268 0.448 0.284
#> GSM907865 2 0.9882 0.0291 0.280 0.408 0.312
#> GSM907868 2 0.6205 0.3632 0.008 0.656 0.336
#> GSM907869 3 0.5413 0.8424 0.036 0.164 0.800
#> GSM907870 2 0.4556 0.6427 0.080 0.860 0.060
#> GSM907861 2 0.5835 0.3580 0.000 0.660 0.340
#> GSM907862 2 0.4862 0.6341 0.020 0.820 0.160
#> GSM907863 2 0.4862 0.6341 0.020 0.820 0.160
#> GSM907866 3 0.4654 0.8450 0.000 0.208 0.792
#> GSM907867 2 0.1989 0.6860 0.004 0.948 0.048
#> GSM907839 2 0.9741 0.0978 0.268 0.448 0.284
#> GSM907840 2 0.9741 0.0978 0.268 0.448 0.284
#> GSM907842 2 0.7474 0.4499 0.216 0.684 0.100
#> GSM907843 2 0.3973 0.6511 0.088 0.880 0.032
#> GSM907845 2 0.7153 0.4654 0.092 0.708 0.200
#> GSM907846 2 0.2269 0.6785 0.040 0.944 0.016
#> GSM907848 2 0.0592 0.6891 0.000 0.988 0.012
#> GSM907851 2 0.4565 0.6423 0.076 0.860 0.064
#> GSM907835 2 0.0237 0.6882 0.000 0.996 0.004
#> GSM907836 2 0.0424 0.6877 0.000 0.992 0.008
#> GSM907837 2 0.1453 0.6867 0.008 0.968 0.024
#> GSM907838 2 0.1453 0.6867 0.008 0.968 0.024
#> GSM907841 3 0.4654 0.8450 0.000 0.208 0.792
#> GSM907844 2 0.1765 0.6863 0.004 0.956 0.040
#> GSM907847 2 0.0592 0.6891 0.000 0.988 0.012
#> GSM907849 2 0.3406 0.6657 0.068 0.904 0.028
#> GSM907850 2 0.0592 0.6890 0.000 0.988 0.012
#> GSM907852 2 0.0237 0.6882 0.000 0.996 0.004
#> GSM907853 2 0.0592 0.6891 0.000 0.988 0.012
#> GSM907807 1 0.0237 0.7179 0.996 0.004 0.000
#> GSM907813 1 0.1525 0.6966 0.964 0.004 0.032
#> GSM907814 1 0.1525 0.6966 0.964 0.004 0.032
#> GSM907816 1 0.1525 0.7272 0.964 0.032 0.004
#> GSM907818 1 0.9198 0.4339 0.528 0.280 0.192
#> GSM907819 1 0.7583 0.2638 0.492 0.468 0.040
#> GSM907820 2 0.7665 -0.2078 0.456 0.500 0.044
#> GSM907822 1 0.4589 0.7031 0.820 0.172 0.008
#> GSM907823 1 0.5728 0.6372 0.772 0.196 0.032
#> GSM907808 1 0.0475 0.7180 0.992 0.004 0.004
#> GSM907809 1 0.0475 0.7180 0.992 0.004 0.004
#> GSM907810 1 0.2945 0.7256 0.908 0.088 0.004
#> GSM907811 1 0.5036 0.7000 0.808 0.172 0.020
#> GSM907812 1 0.6284 0.5037 0.680 0.016 0.304
#> GSM907815 3 0.4897 0.6177 0.172 0.016 0.812
#> GSM907817 2 0.7668 -0.2190 0.460 0.496 0.044
#> GSM907821 2 0.7665 -0.2078 0.456 0.500 0.044
#> GSM907824 2 0.7665 -0.2078 0.456 0.500 0.044
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.6926 0.0993 0.000 0.432 0.460 0.108
#> GSM907859 4 0.5812 0.9391 0.136 0.156 0.000 0.708
#> GSM907860 2 0.6915 0.3883 0.000 0.564 0.140 0.296
#> GSM907854 3 0.6967 0.0992 0.000 0.432 0.456 0.112
#> GSM907855 2 0.7557 0.2001 0.000 0.488 0.260 0.252
#> GSM907856 2 0.7557 0.2001 0.000 0.488 0.260 0.252
#> GSM907857 3 0.4224 0.6394 0.000 0.076 0.824 0.100
#> GSM907825 2 0.4163 0.6979 0.000 0.828 0.096 0.076
#> GSM907828 2 0.6311 0.6448 0.064 0.708 0.048 0.180
#> GSM907832 2 0.3216 0.7037 0.004 0.864 0.008 0.124
#> GSM907833 2 0.1557 0.7469 0.000 0.944 0.000 0.056
#> GSM907834 2 0.4022 0.6985 0.000 0.836 0.096 0.068
#> GSM907826 2 0.0895 0.7511 0.000 0.976 0.020 0.004
#> GSM907827 2 0.4188 0.6930 0.000 0.824 0.112 0.064
#> GSM907829 2 0.5219 0.6111 0.000 0.728 0.216 0.056
#> GSM907830 2 0.5356 0.6546 0.000 0.728 0.072 0.200
#> GSM907831 2 0.4336 0.6756 0.000 0.812 0.128 0.060
#> GSM907792 1 0.3071 0.6641 0.888 0.068 0.000 0.044
#> GSM907795 1 0.1557 0.6380 0.944 0.000 0.000 0.056
#> GSM907801 1 0.1557 0.6380 0.944 0.000 0.000 0.056
#> GSM907802 1 0.7242 0.5152 0.496 0.380 0.008 0.116
#> GSM907804 1 0.7153 0.5436 0.520 0.360 0.008 0.112
#> GSM907805 1 0.7887 0.6163 0.600 0.176 0.144 0.080
#> GSM907806 1 0.3450 0.6749 0.836 0.156 0.000 0.008
#> GSM907793 1 0.1389 0.6443 0.952 0.000 0.000 0.048
#> GSM907794 1 0.6986 0.5961 0.568 0.312 0.008 0.112
#> GSM907796 1 0.6009 0.5065 0.656 0.008 0.280 0.056
#> GSM907797 1 0.6207 0.4648 0.620 0.008 0.316 0.056
#> GSM907798 1 0.6009 0.5065 0.656 0.008 0.280 0.056
#> GSM907799 1 0.3142 0.6809 0.860 0.132 0.000 0.008
#> GSM907800 1 0.7191 0.5231 0.504 0.376 0.008 0.112
#> GSM907803 1 0.3142 0.6809 0.860 0.132 0.000 0.008
#> GSM907864 4 0.5849 0.9668 0.132 0.164 0.000 0.704
#> GSM907865 4 0.5380 0.9306 0.136 0.120 0.000 0.744
#> GSM907868 2 0.7082 0.0399 0.000 0.500 0.368 0.132
#> GSM907869 3 0.2463 0.6345 0.008 0.032 0.924 0.036
#> GSM907870 2 0.4171 0.6640 0.060 0.824 0.000 0.116
#> GSM907861 2 0.6894 0.0503 0.000 0.512 0.376 0.112
#> GSM907862 2 0.6620 0.4378 0.000 0.576 0.104 0.320
#> GSM907863 2 0.6620 0.4378 0.000 0.576 0.104 0.320
#> GSM907866 3 0.2266 0.6568 0.000 0.084 0.912 0.004
#> GSM907867 2 0.2775 0.7317 0.000 0.896 0.084 0.020
#> GSM907839 4 0.5849 0.9668 0.132 0.164 0.000 0.704
#> GSM907840 4 0.5849 0.9668 0.132 0.164 0.000 0.704
#> GSM907842 2 0.6613 0.1883 0.116 0.596 0.000 0.288
#> GSM907843 2 0.3820 0.6822 0.064 0.848 0.000 0.088
#> GSM907845 2 0.7993 0.4129 0.092 0.588 0.200 0.120
#> GSM907846 2 0.4397 0.6713 0.052 0.820 0.008 0.120
#> GSM907848 2 0.1557 0.7469 0.000 0.944 0.000 0.056
#> GSM907851 2 0.4150 0.6638 0.056 0.824 0.000 0.120
#> GSM907835 2 0.0188 0.7504 0.000 0.996 0.000 0.004
#> GSM907836 2 0.0376 0.7502 0.000 0.992 0.004 0.004
#> GSM907837 2 0.1118 0.7517 0.000 0.964 0.000 0.036
#> GSM907838 2 0.1118 0.7517 0.000 0.964 0.000 0.036
#> GSM907841 3 0.2266 0.6568 0.000 0.084 0.912 0.004
#> GSM907844 2 0.2593 0.7330 0.000 0.904 0.080 0.016
#> GSM907847 2 0.1557 0.7469 0.000 0.944 0.000 0.056
#> GSM907849 2 0.3354 0.7074 0.044 0.872 0.000 0.084
#> GSM907850 2 0.1118 0.7496 0.000 0.964 0.000 0.036
#> GSM907852 2 0.0000 0.7500 0.000 1.000 0.000 0.000
#> GSM907853 2 0.1557 0.7469 0.000 0.944 0.000 0.056
#> GSM907807 1 0.1557 0.6380 0.944 0.000 0.000 0.056
#> GSM907813 1 0.2345 0.6081 0.900 0.000 0.000 0.100
#> GSM907814 1 0.2345 0.6081 0.900 0.000 0.000 0.100
#> GSM907816 1 0.2197 0.6525 0.928 0.024 0.000 0.048
#> GSM907818 1 0.8376 0.5805 0.540 0.220 0.160 0.080
#> GSM907819 1 0.7119 0.5599 0.532 0.348 0.008 0.112
#> GSM907820 1 0.7242 0.5152 0.496 0.380 0.008 0.116
#> GSM907822 1 0.3377 0.6778 0.848 0.140 0.000 0.012
#> GSM907823 1 0.5325 0.6004 0.744 0.160 0.000 0.096
#> GSM907808 1 0.1637 0.6387 0.940 0.000 0.000 0.060
#> GSM907809 1 0.1637 0.6387 0.940 0.000 0.000 0.060
#> GSM907810 1 0.3266 0.6679 0.876 0.084 0.000 0.040
#> GSM907811 1 0.3249 0.6790 0.852 0.140 0.000 0.008
#> GSM907812 1 0.6009 0.5065 0.656 0.008 0.280 0.056
#> GSM907815 3 0.4078 0.4255 0.132 0.004 0.828 0.036
#> GSM907817 1 0.7200 0.5177 0.500 0.380 0.008 0.112
#> GSM907821 1 0.7242 0.5152 0.496 0.380 0.008 0.116
#> GSM907824 1 0.7242 0.5152 0.496 0.380 0.008 0.116
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.581 0.2361 0.084 0.384 0.528 0.000 0.004
#> GSM907859 4 0.245 0.9246 0.044 0.056 0.000 0.900 0.000
#> GSM907860 2 0.737 0.2433 0.080 0.520 0.204 0.196 0.000
#> GSM907854 3 0.592 0.2377 0.084 0.384 0.524 0.000 0.008
#> GSM907855 2 0.753 0.0577 0.084 0.448 0.324 0.144 0.000
#> GSM907856 2 0.753 0.0577 0.084 0.448 0.324 0.144 0.000
#> GSM907857 3 0.281 0.6415 0.084 0.032 0.880 0.000 0.004
#> GSM907825 2 0.384 0.6336 0.004 0.804 0.148 0.000 0.044
#> GSM907828 2 0.556 0.6136 0.008 0.684 0.092 0.204 0.012
#> GSM907832 2 0.417 0.6353 0.000 0.760 0.000 0.048 0.192
#> GSM907833 2 0.290 0.7018 0.000 0.872 0.000 0.048 0.080
#> GSM907834 2 0.353 0.6329 0.004 0.820 0.148 0.000 0.028
#> GSM907826 2 0.157 0.7071 0.000 0.944 0.020 0.000 0.036
#> GSM907827 2 0.358 0.6235 0.004 0.812 0.164 0.016 0.004
#> GSM907829 2 0.404 0.5391 0.004 0.720 0.268 0.000 0.008
#> GSM907830 2 0.502 0.6063 0.000 0.716 0.116 0.164 0.004
#> GSM907831 2 0.337 0.6067 0.004 0.808 0.180 0.000 0.008
#> GSM907792 1 0.395 0.6690 0.696 0.004 0.000 0.000 0.300
#> GSM907795 1 0.260 0.8199 0.852 0.000 0.000 0.000 0.148
#> GSM907801 1 0.269 0.8216 0.844 0.000 0.000 0.000 0.156
#> GSM907802 5 0.185 0.6133 0.000 0.088 0.000 0.000 0.912
#> GSM907804 5 0.260 0.6060 0.032 0.080 0.000 0.000 0.888
#> GSM907805 5 0.587 0.4442 0.172 0.028 0.120 0.004 0.676
#> GSM907806 5 0.504 -0.2055 0.460 0.032 0.000 0.000 0.508
#> GSM907793 1 0.281 0.8167 0.832 0.000 0.000 0.000 0.168
#> GSM907794 5 0.342 0.5769 0.088 0.072 0.000 0.000 0.840
#> GSM907796 5 0.704 0.1435 0.336 0.000 0.252 0.012 0.400
#> GSM907797 5 0.706 0.1637 0.292 0.000 0.288 0.012 0.408
#> GSM907798 5 0.704 0.1435 0.336 0.000 0.252 0.012 0.400
#> GSM907799 5 0.491 -0.2611 0.480 0.024 0.000 0.000 0.496
#> GSM907800 5 0.214 0.6131 0.008 0.088 0.000 0.000 0.904
#> GSM907803 5 0.491 -0.2715 0.484 0.024 0.000 0.000 0.492
#> GSM907864 4 0.156 0.9647 0.008 0.052 0.000 0.940 0.000
#> GSM907865 4 0.140 0.9339 0.028 0.020 0.000 0.952 0.000
#> GSM907868 2 0.647 -0.1198 0.084 0.452 0.436 0.024 0.004
#> GSM907869 3 0.231 0.6452 0.012 0.032 0.920 0.004 0.032
#> GSM907870 2 0.465 0.6474 0.008 0.748 0.000 0.172 0.072
#> GSM907861 2 0.599 -0.1165 0.084 0.464 0.444 0.000 0.008
#> GSM907862 2 0.727 0.2964 0.080 0.532 0.168 0.220 0.000
#> GSM907863 2 0.727 0.2964 0.080 0.532 0.168 0.220 0.000
#> GSM907866 3 0.349 0.6690 0.024 0.072 0.864 0.020 0.020
#> GSM907867 2 0.316 0.6850 0.000 0.864 0.092 0.012 0.032
#> GSM907839 4 0.156 0.9647 0.008 0.052 0.000 0.940 0.000
#> GSM907840 4 0.156 0.9647 0.008 0.052 0.000 0.940 0.000
#> GSM907842 2 0.549 0.2881 0.008 0.540 0.000 0.404 0.048
#> GSM907843 2 0.429 0.6674 0.008 0.780 0.000 0.148 0.064
#> GSM907845 2 0.716 0.2647 0.040 0.520 0.240 0.004 0.196
#> GSM907846 2 0.531 0.4828 0.004 0.616 0.004 0.048 0.328
#> GSM907848 2 0.290 0.7018 0.000 0.872 0.000 0.048 0.080
#> GSM907851 2 0.463 0.6476 0.008 0.748 0.000 0.176 0.068
#> GSM907835 2 0.133 0.7085 0.000 0.952 0.000 0.008 0.040
#> GSM907836 2 0.112 0.7079 0.000 0.960 0.004 0.000 0.036
#> GSM907837 2 0.208 0.7098 0.000 0.920 0.000 0.040 0.040
#> GSM907838 2 0.208 0.7098 0.000 0.920 0.000 0.040 0.040
#> GSM907841 3 0.349 0.6690 0.024 0.072 0.864 0.020 0.020
#> GSM907844 2 0.300 0.6859 0.000 0.872 0.088 0.008 0.032
#> GSM907847 2 0.290 0.7018 0.000 0.872 0.000 0.048 0.080
#> GSM907849 2 0.396 0.6812 0.004 0.804 0.000 0.128 0.064
#> GSM907850 2 0.250 0.7050 0.000 0.896 0.000 0.040 0.064
#> GSM907852 2 0.120 0.7080 0.000 0.956 0.000 0.004 0.040
#> GSM907853 2 0.290 0.7018 0.000 0.872 0.000 0.048 0.080
#> GSM907807 1 0.265 0.8216 0.848 0.000 0.000 0.000 0.152
#> GSM907813 1 0.285 0.7827 0.868 0.000 0.000 0.028 0.104
#> GSM907814 1 0.285 0.7827 0.868 0.000 0.000 0.028 0.104
#> GSM907816 1 0.342 0.7812 0.788 0.008 0.000 0.000 0.204
#> GSM907818 5 0.539 0.5163 0.084 0.044 0.136 0.004 0.732
#> GSM907819 5 0.277 0.6022 0.044 0.076 0.000 0.000 0.880
#> GSM907820 5 0.185 0.6133 0.000 0.088 0.000 0.000 0.912
#> GSM907822 1 0.497 0.2540 0.508 0.028 0.000 0.000 0.464
#> GSM907823 1 0.670 0.3577 0.500 0.056 0.000 0.080 0.364
#> GSM907808 1 0.281 0.8211 0.844 0.000 0.000 0.004 0.152
#> GSM907809 1 0.281 0.8211 0.844 0.000 0.000 0.004 0.152
#> GSM907810 1 0.447 0.5310 0.616 0.012 0.000 0.000 0.372
#> GSM907811 5 0.497 -0.2181 0.464 0.028 0.000 0.000 0.508
#> GSM907812 5 0.704 0.1435 0.336 0.000 0.252 0.012 0.400
#> GSM907815 3 0.498 0.4344 0.128 0.000 0.752 0.032 0.088
#> GSM907817 5 0.201 0.6133 0.004 0.088 0.000 0.000 0.908
#> GSM907821 5 0.185 0.6133 0.000 0.088 0.000 0.000 0.912
#> GSM907824 5 0.185 0.6133 0.000 0.088 0.000 0.000 0.912
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.2420 0.55446 0.000 0.040 0.884 0.000 0.000 0.076
#> GSM907859 4 0.1564 0.91936 0.024 0.040 0.000 0.936 0.000 0.000
#> GSM907860 3 0.5136 0.62900 0.000 0.160 0.640 0.196 0.004 0.000
#> GSM907854 3 0.2685 0.55337 0.000 0.044 0.872 0.000 0.004 0.080
#> GSM907855 3 0.4225 0.65132 0.000 0.096 0.752 0.144 0.000 0.008
#> GSM907856 3 0.4225 0.65132 0.000 0.096 0.752 0.144 0.000 0.008
#> GSM907857 3 0.3774 -0.13616 0.000 0.000 0.592 0.000 0.000 0.408
#> GSM907825 2 0.4726 0.09812 0.000 0.528 0.424 0.000 0.048 0.000
#> GSM907828 2 0.5624 0.35699 0.000 0.576 0.228 0.188 0.008 0.000
#> GSM907832 2 0.3313 0.66440 0.000 0.808 0.008 0.024 0.160 0.000
#> GSM907833 2 0.2342 0.72452 0.000 0.904 0.032 0.024 0.040 0.000
#> GSM907834 2 0.4453 0.07301 0.000 0.528 0.444 0.000 0.028 0.000
#> GSM907826 2 0.2762 0.63506 0.000 0.804 0.196 0.000 0.000 0.000
#> GSM907827 2 0.4403 0.00171 0.000 0.520 0.460 0.012 0.008 0.000
#> GSM907829 3 0.5153 0.18549 0.000 0.404 0.528 0.000 0.016 0.052
#> GSM907830 2 0.5786 0.09895 0.000 0.504 0.336 0.152 0.008 0.000
#> GSM907831 3 0.4246 0.08821 0.000 0.452 0.532 0.000 0.016 0.000
#> GSM907792 1 0.2883 0.68753 0.788 0.000 0.000 0.000 0.212 0.000
#> GSM907795 1 0.0260 0.71877 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907801 1 0.0547 0.72431 0.980 0.000 0.000 0.000 0.020 0.000
#> GSM907802 5 0.0622 0.89936 0.008 0.012 0.000 0.000 0.980 0.000
#> GSM907804 5 0.1196 0.88847 0.040 0.008 0.000 0.000 0.952 0.000
#> GSM907805 5 0.4950 0.54189 0.164 0.000 0.000 0.000 0.652 0.184
#> GSM907806 1 0.3866 0.38462 0.516 0.000 0.000 0.000 0.484 0.000
#> GSM907793 1 0.0713 0.72395 0.972 0.000 0.000 0.000 0.028 0.000
#> GSM907794 5 0.2288 0.80765 0.116 0.004 0.000 0.000 0.876 0.004
#> GSM907796 6 0.5980 0.40064 0.264 0.000 0.000 0.000 0.292 0.444
#> GSM907797 6 0.5658 0.39795 0.188 0.000 0.000 0.000 0.292 0.520
#> GSM907798 6 0.5980 0.40064 0.264 0.000 0.000 0.000 0.292 0.444
#> GSM907799 1 0.3847 0.45003 0.544 0.000 0.000 0.000 0.456 0.000
#> GSM907800 5 0.0820 0.89855 0.016 0.012 0.000 0.000 0.972 0.000
#> GSM907803 1 0.3843 0.45669 0.548 0.000 0.000 0.000 0.452 0.000
#> GSM907864 4 0.1007 0.96186 0.000 0.044 0.000 0.956 0.000 0.000
#> GSM907865 4 0.0260 0.92893 0.008 0.000 0.000 0.992 0.000 0.000
#> GSM907868 3 0.3988 0.63624 0.000 0.120 0.788 0.024 0.000 0.068
#> GSM907869 6 0.3817 0.20940 0.000 0.000 0.432 0.000 0.000 0.568
#> GSM907870 2 0.3377 0.66751 0.000 0.816 0.004 0.140 0.036 0.004
#> GSM907861 3 0.3782 0.62350 0.000 0.140 0.784 0.000 0.004 0.072
#> GSM907862 3 0.5508 0.60193 0.000 0.200 0.584 0.212 0.004 0.000
#> GSM907863 3 0.5508 0.60193 0.000 0.200 0.584 0.212 0.004 0.000
#> GSM907866 6 0.3804 0.20013 0.000 0.000 0.424 0.000 0.000 0.576
#> GSM907867 2 0.3852 0.43457 0.000 0.664 0.324 0.012 0.000 0.000
#> GSM907839 4 0.1007 0.96186 0.000 0.044 0.000 0.956 0.000 0.000
#> GSM907840 4 0.1007 0.96186 0.000 0.044 0.000 0.956 0.000 0.000
#> GSM907842 2 0.4209 0.40640 0.000 0.596 0.000 0.384 0.020 0.000
#> GSM907843 2 0.2848 0.68904 0.000 0.848 0.004 0.124 0.024 0.000
#> GSM907845 3 0.7870 0.15438 0.020 0.296 0.340 0.000 0.184 0.160
#> GSM907846 2 0.5818 0.40178 0.008 0.548 0.076 0.024 0.340 0.004
#> GSM907848 2 0.2342 0.72452 0.000 0.904 0.032 0.024 0.040 0.000
#> GSM907851 2 0.3130 0.67239 0.000 0.824 0.004 0.144 0.028 0.000
#> GSM907835 2 0.1327 0.71058 0.000 0.936 0.064 0.000 0.000 0.000
#> GSM907836 2 0.2219 0.67671 0.000 0.864 0.136 0.000 0.000 0.000
#> GSM907837 2 0.1334 0.71731 0.000 0.948 0.032 0.020 0.000 0.000
#> GSM907838 2 0.1334 0.71731 0.000 0.948 0.032 0.020 0.000 0.000
#> GSM907841 6 0.3804 0.20013 0.000 0.000 0.424 0.000 0.000 0.576
#> GSM907844 2 0.3725 0.45434 0.000 0.676 0.316 0.008 0.000 0.000
#> GSM907847 2 0.2342 0.72452 0.000 0.904 0.032 0.024 0.040 0.000
#> GSM907849 2 0.2526 0.70147 0.000 0.876 0.004 0.096 0.024 0.000
#> GSM907850 2 0.2255 0.72445 0.000 0.908 0.044 0.024 0.024 0.000
#> GSM907852 2 0.1333 0.71636 0.000 0.944 0.048 0.000 0.008 0.000
#> GSM907853 2 0.2415 0.72466 0.000 0.900 0.036 0.024 0.040 0.000
#> GSM907807 1 0.0363 0.72130 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907813 1 0.0937 0.69335 0.960 0.000 0.000 0.040 0.000 0.000
#> GSM907814 1 0.0937 0.69335 0.960 0.000 0.000 0.040 0.000 0.000
#> GSM907816 1 0.1610 0.71824 0.916 0.000 0.000 0.000 0.084 0.000
#> GSM907818 5 0.4255 0.64002 0.064 0.008 0.000 0.000 0.732 0.196
#> GSM907819 5 0.1542 0.88078 0.052 0.008 0.000 0.000 0.936 0.004
#> GSM907820 5 0.0622 0.89936 0.008 0.012 0.000 0.000 0.980 0.000
#> GSM907822 1 0.3789 0.51000 0.584 0.000 0.000 0.000 0.416 0.000
#> GSM907823 1 0.5821 0.53320 0.580 0.048 0.004 0.064 0.300 0.004
#> GSM907808 1 0.0508 0.72046 0.984 0.000 0.000 0.000 0.012 0.004
#> GSM907809 1 0.0508 0.72046 0.984 0.000 0.000 0.000 0.012 0.004
#> GSM907810 1 0.3428 0.62612 0.696 0.000 0.000 0.000 0.304 0.000
#> GSM907811 1 0.3860 0.41826 0.528 0.000 0.000 0.000 0.472 0.000
#> GSM907812 6 0.5980 0.40064 0.264 0.000 0.000 0.000 0.292 0.444
#> GSM907815 6 0.1584 0.41050 0.000 0.000 0.064 0.000 0.008 0.928
#> GSM907817 5 0.0725 0.89956 0.012 0.012 0.000 0.000 0.976 0.000
#> GSM907821 5 0.0622 0.89936 0.008 0.012 0.000 0.000 0.980 0.000
#> GSM907824 5 0.0622 0.89936 0.008 0.012 0.000 0.000 0.980 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
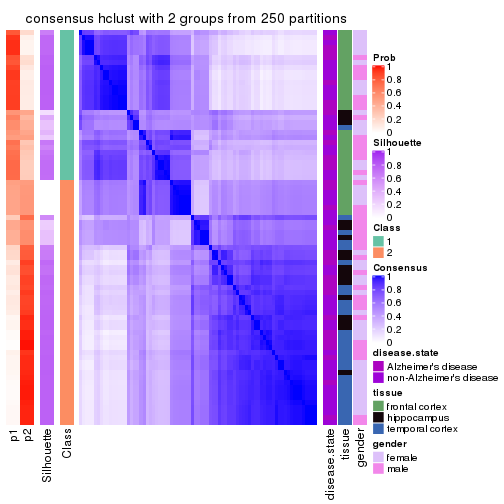
consensus_heatmap(res, k = 3)
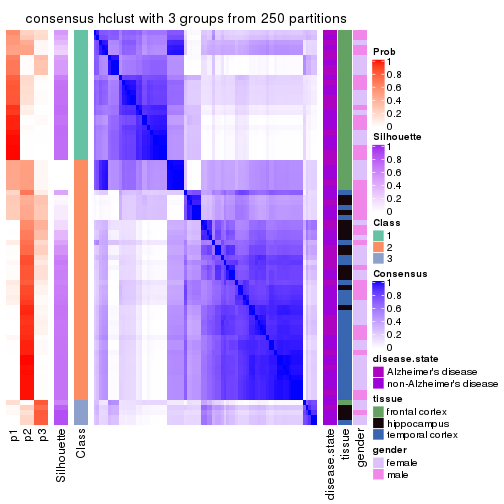
consensus_heatmap(res, k = 4)
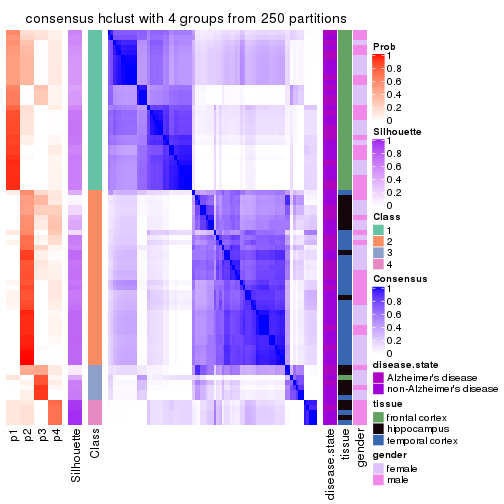
consensus_heatmap(res, k = 5)
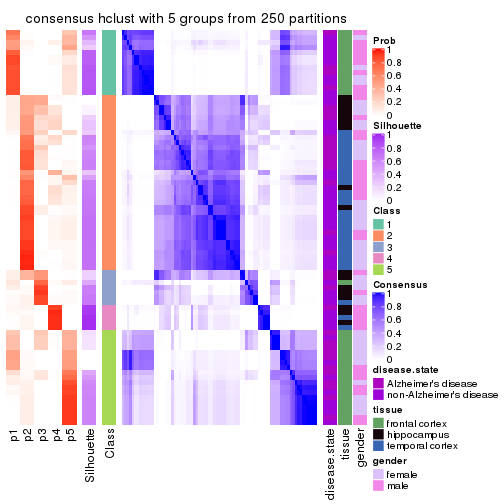
consensus_heatmap(res, k = 6)
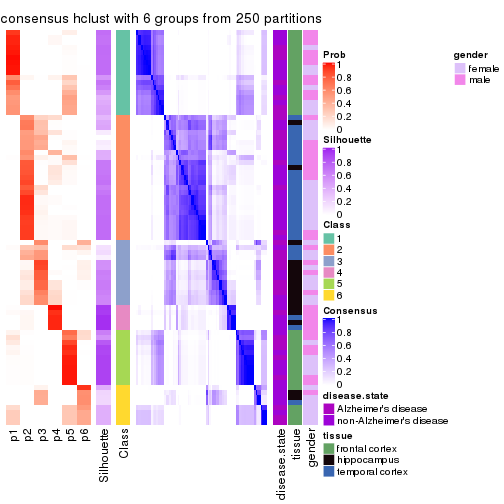
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
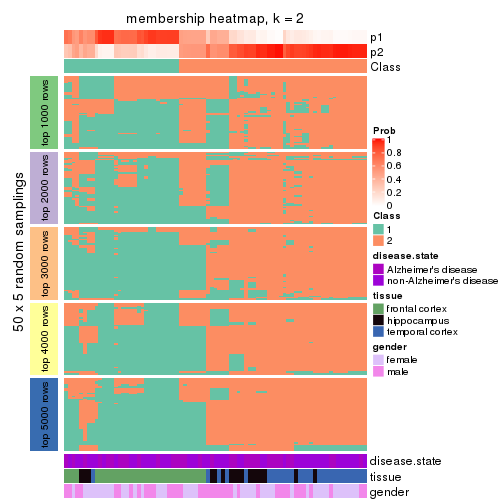
membership_heatmap(res, k = 3)
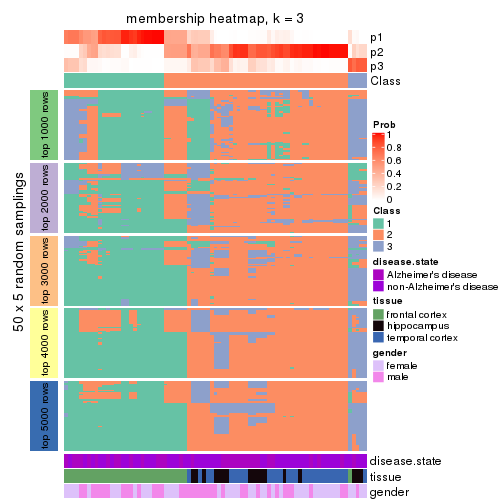
membership_heatmap(res, k = 4)
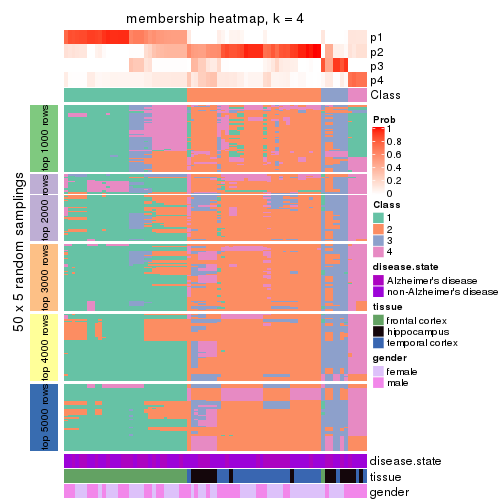
membership_heatmap(res, k = 5)
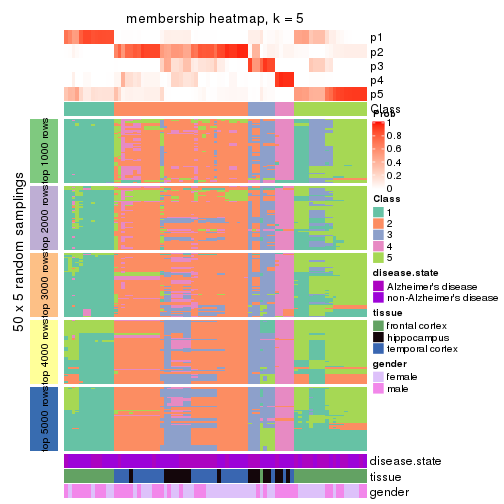
membership_heatmap(res, k = 6)
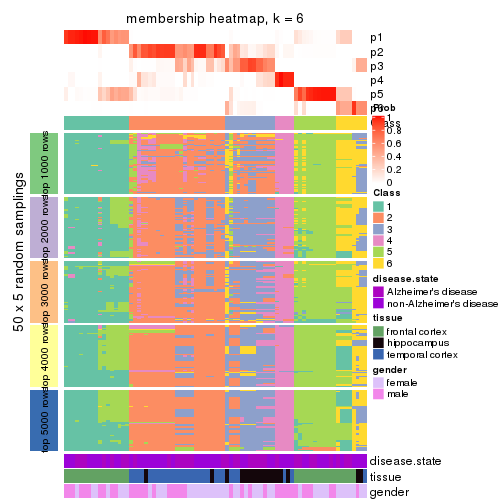
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
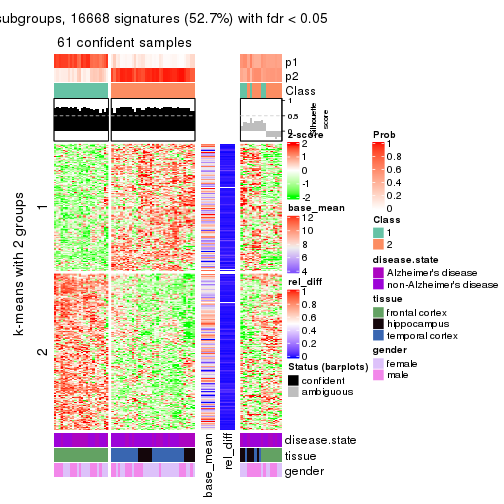
get_signatures(res, k = 3)
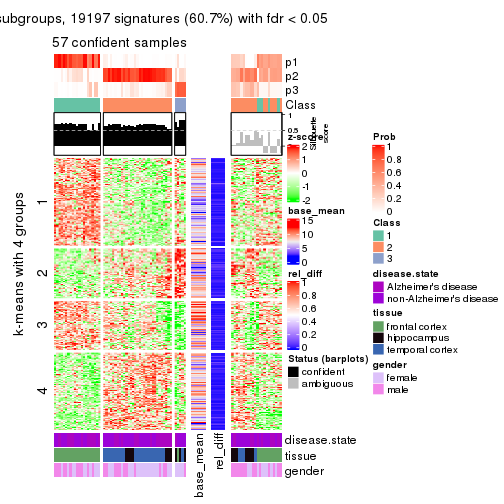
get_signatures(res, k = 4)
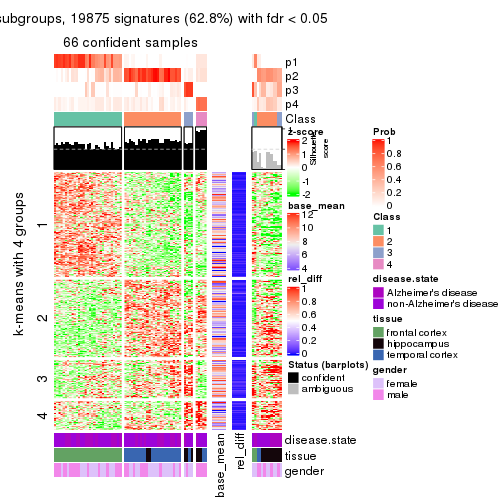
get_signatures(res, k = 5)
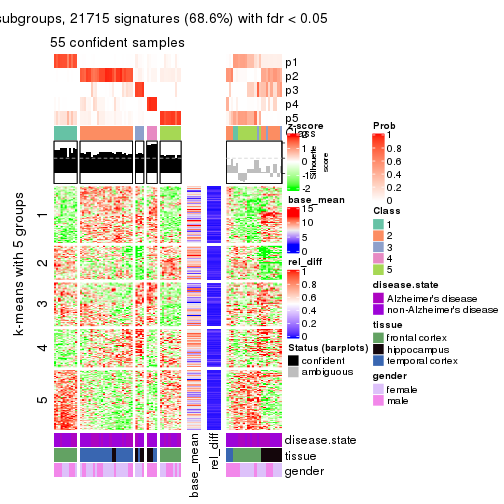
get_signatures(res, k = 6)
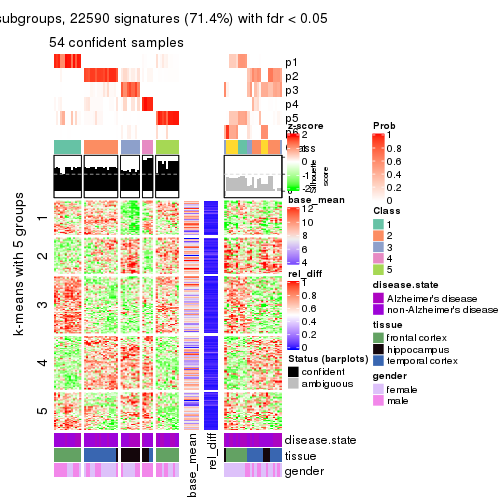
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
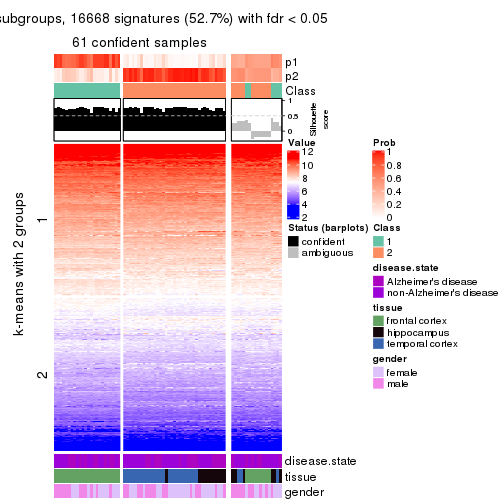
get_signatures(res, k = 3, scale_rows = FALSE)
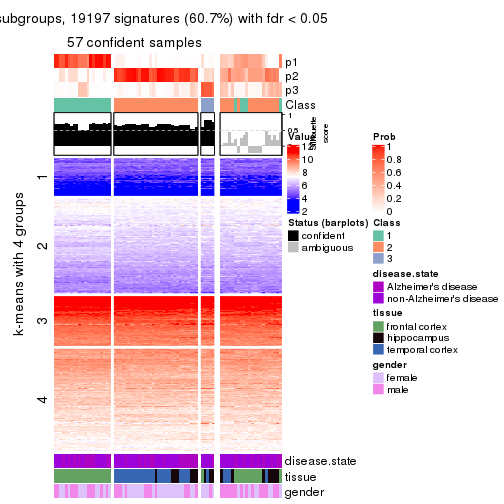
get_signatures(res, k = 4, scale_rows = FALSE)
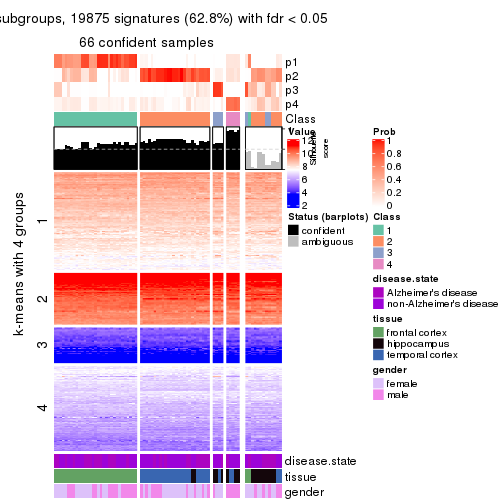
get_signatures(res, k = 5, scale_rows = FALSE)
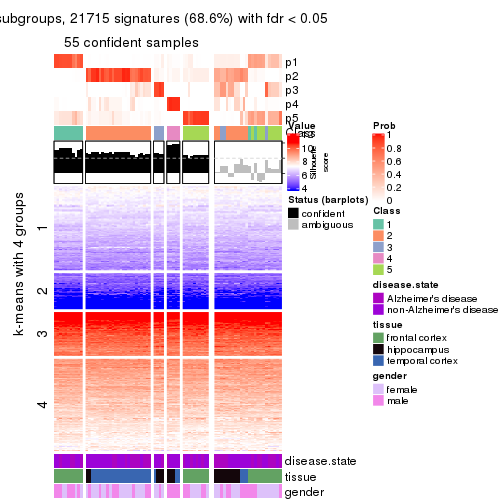
get_signatures(res, k = 6, scale_rows = FALSE)
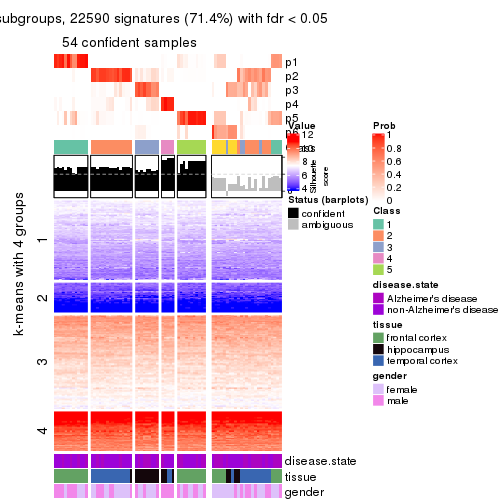
Compare the overlap of signatures from different k:
compare_signatures(res)
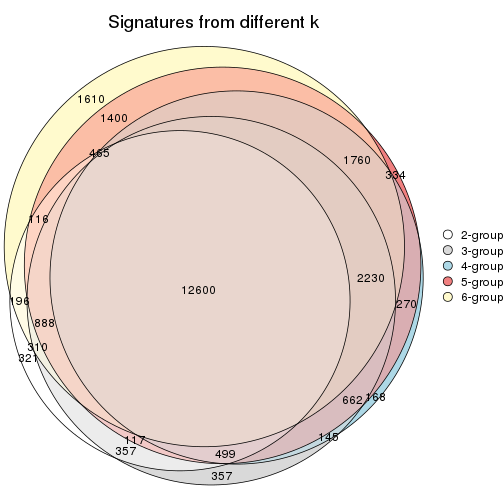
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
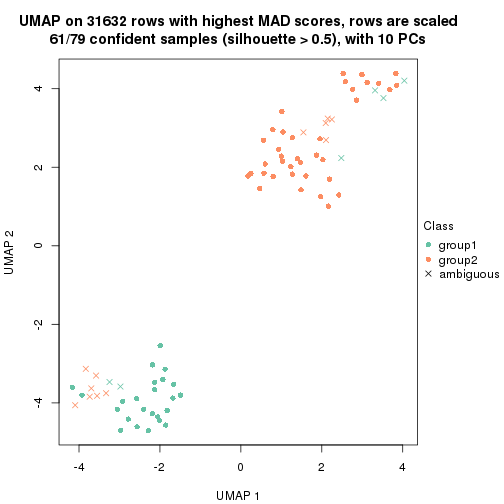
dimension_reduction(res, k = 3, method = "UMAP")
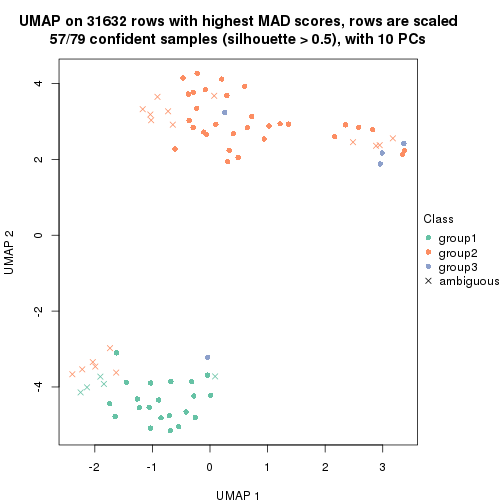
dimension_reduction(res, k = 4, method = "UMAP")
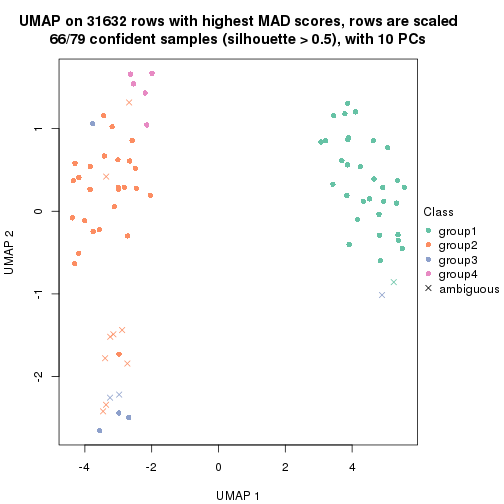
dimension_reduction(res, k = 5, method = "UMAP")
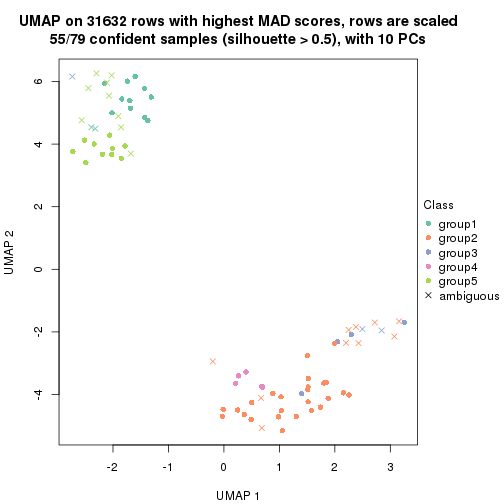
dimension_reduction(res, k = 6, method = "UMAP")
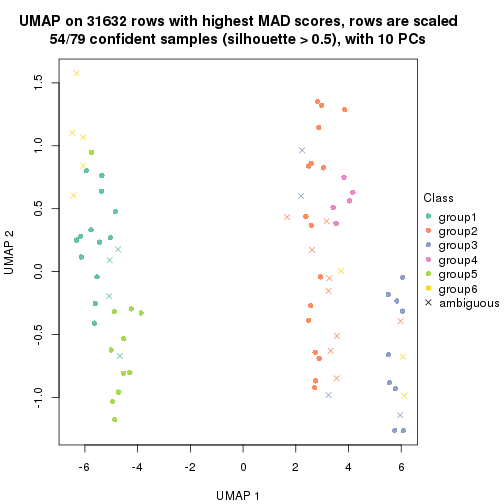
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
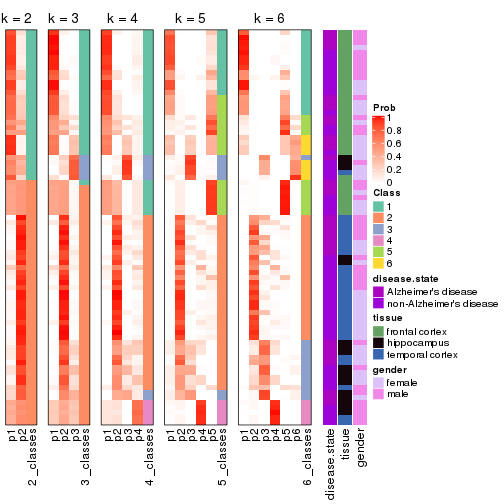
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:hclust 61 0.886 5.68e-14 0.6435 2
#> MAD:hclust 57 0.531 2.88e-12 0.2970 3
#> MAD:hclust 66 0.665 1.55e-17 0.0612 4
#> MAD:hclust 55 0.910 3.22e-13 0.0673 5
#> MAD:hclust 54 0.320 1.56e-16 0.0672 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "kmeans"]
# you can also extract it by
# res = res_list["MAD:kmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'kmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
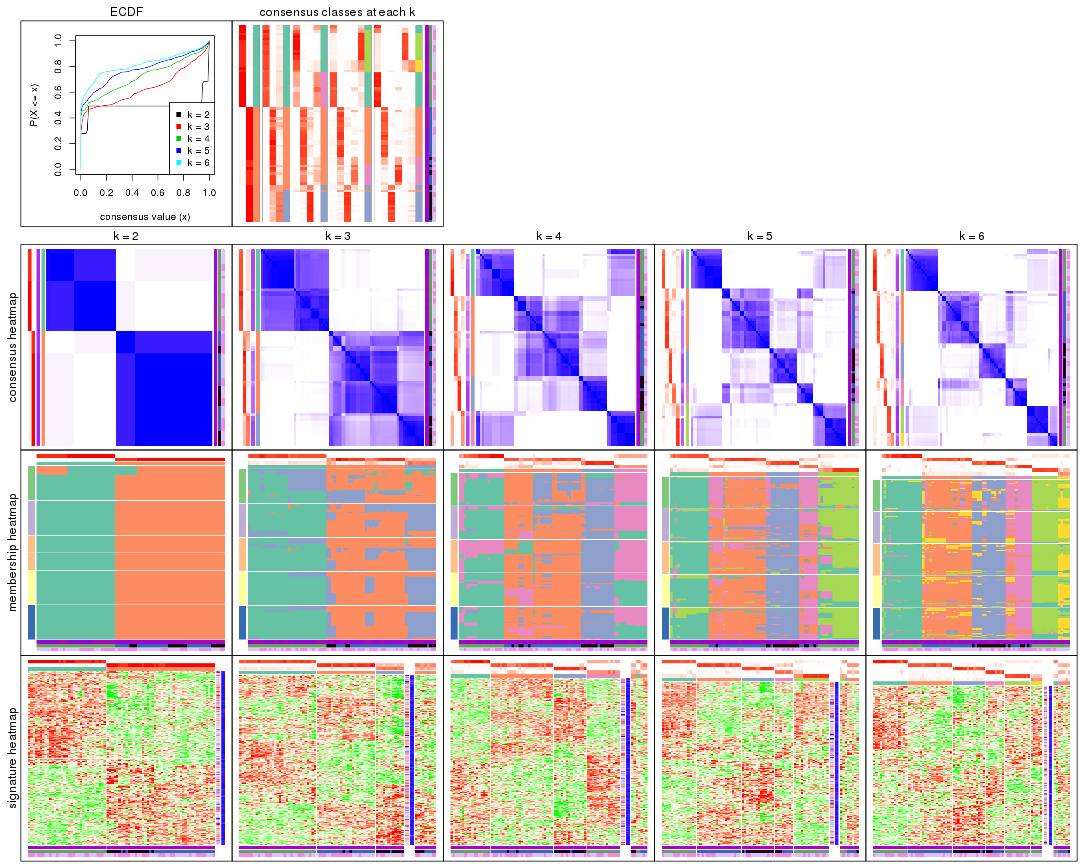
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
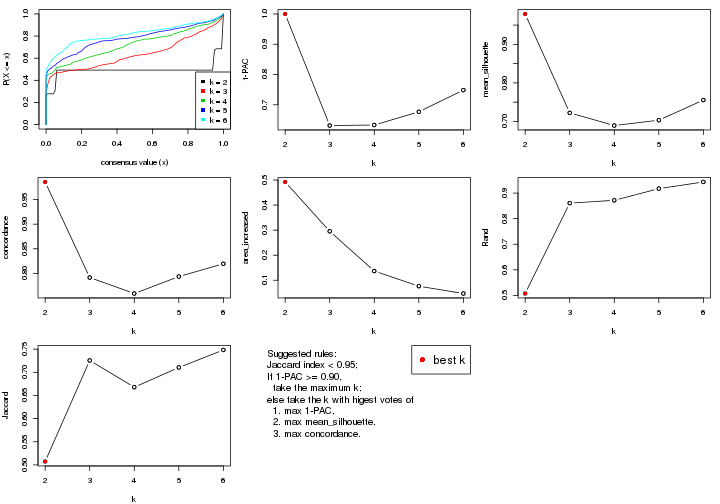
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.979 0.986 0.4922 0.507 0.507
#> 3 3 0.631 0.722 0.792 0.2954 0.861 0.726
#> 4 4 0.633 0.690 0.759 0.1367 0.872 0.668
#> 5 5 0.677 0.703 0.794 0.0763 0.918 0.710
#> 6 6 0.748 0.756 0.820 0.0471 0.944 0.748
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.000 0.989 0.000 1.000
#> GSM907859 2 0.295 0.955 0.052 0.948
#> GSM907860 2 0.000 0.989 0.000 1.000
#> GSM907854 2 0.000 0.989 0.000 1.000
#> GSM907855 2 0.000 0.989 0.000 1.000
#> GSM907856 2 0.000 0.989 0.000 1.000
#> GSM907857 2 0.000 0.989 0.000 1.000
#> GSM907825 2 0.000 0.989 0.000 1.000
#> GSM907828 2 0.000 0.989 0.000 1.000
#> GSM907832 2 0.000 0.989 0.000 1.000
#> GSM907833 2 0.000 0.989 0.000 1.000
#> GSM907834 2 0.000 0.989 0.000 1.000
#> GSM907826 2 0.000 0.989 0.000 1.000
#> GSM907827 2 0.000 0.989 0.000 1.000
#> GSM907829 2 0.000 0.989 0.000 1.000
#> GSM907830 2 0.000 0.989 0.000 1.000
#> GSM907831 2 0.000 0.989 0.000 1.000
#> GSM907792 1 0.000 0.979 1.000 0.000
#> GSM907795 1 0.000 0.979 1.000 0.000
#> GSM907801 1 0.000 0.979 1.000 0.000
#> GSM907802 1 0.295 0.965 0.948 0.052
#> GSM907804 1 0.000 0.979 1.000 0.000
#> GSM907805 1 0.000 0.979 1.000 0.000
#> GSM907806 1 0.000 0.979 1.000 0.000
#> GSM907793 1 0.000 0.979 1.000 0.000
#> GSM907794 1 0.260 0.968 0.956 0.044
#> GSM907796 1 0.295 0.965 0.948 0.052
#> GSM907797 1 0.295 0.965 0.948 0.052
#> GSM907798 1 0.295 0.965 0.948 0.052
#> GSM907799 1 0.000 0.979 1.000 0.000
#> GSM907800 1 0.260 0.968 0.956 0.044
#> GSM907803 1 0.000 0.979 1.000 0.000
#> GSM907864 2 0.295 0.955 0.052 0.948
#> GSM907865 2 0.295 0.955 0.052 0.948
#> GSM907868 2 0.000 0.989 0.000 1.000
#> GSM907869 2 0.000 0.989 0.000 1.000
#> GSM907870 2 0.000 0.989 0.000 1.000
#> GSM907861 2 0.000 0.989 0.000 1.000
#> GSM907862 2 0.000 0.989 0.000 1.000
#> GSM907863 2 0.000 0.989 0.000 1.000
#> GSM907866 2 0.000 0.989 0.000 1.000
#> GSM907867 2 0.000 0.989 0.000 1.000
#> GSM907839 2 0.295 0.955 0.052 0.948
#> GSM907840 2 0.295 0.955 0.052 0.948
#> GSM907842 2 0.295 0.955 0.052 0.948
#> GSM907843 2 0.295 0.955 0.052 0.948
#> GSM907845 2 0.000 0.989 0.000 1.000
#> GSM907846 2 0.000 0.989 0.000 1.000
#> GSM907848 2 0.000 0.989 0.000 1.000
#> GSM907851 2 0.295 0.955 0.052 0.948
#> GSM907835 2 0.000 0.989 0.000 1.000
#> GSM907836 2 0.000 0.989 0.000 1.000
#> GSM907837 2 0.000 0.989 0.000 1.000
#> GSM907838 2 0.000 0.989 0.000 1.000
#> GSM907841 2 0.000 0.989 0.000 1.000
#> GSM907844 2 0.000 0.989 0.000 1.000
#> GSM907847 2 0.000 0.989 0.000 1.000
#> GSM907849 2 0.295 0.955 0.052 0.948
#> GSM907850 2 0.000 0.989 0.000 1.000
#> GSM907852 2 0.000 0.989 0.000 1.000
#> GSM907853 2 0.000 0.989 0.000 1.000
#> GSM907807 1 0.000 0.979 1.000 0.000
#> GSM907813 1 0.000 0.979 1.000 0.000
#> GSM907814 1 0.000 0.979 1.000 0.000
#> GSM907816 1 0.000 0.979 1.000 0.000
#> GSM907818 1 0.295 0.965 0.948 0.052
#> GSM907819 1 0.295 0.965 0.948 0.052
#> GSM907820 1 0.295 0.965 0.948 0.052
#> GSM907822 1 0.000 0.979 1.000 0.000
#> GSM907823 1 0.000 0.979 1.000 0.000
#> GSM907808 1 0.000 0.979 1.000 0.000
#> GSM907809 1 0.000 0.979 1.000 0.000
#> GSM907810 1 0.000 0.979 1.000 0.000
#> GSM907811 1 0.000 0.979 1.000 0.000
#> GSM907812 1 0.000 0.979 1.000 0.000
#> GSM907815 1 0.295 0.965 0.948 0.052
#> GSM907817 1 0.295 0.965 0.948 0.052
#> GSM907821 1 0.295 0.965 0.948 0.052
#> GSM907824 1 0.295 0.965 0.948 0.052
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.5835 0.8923 0.000 0.340 0.660
#> GSM907859 2 0.5873 0.3725 0.004 0.684 0.312
#> GSM907860 3 0.5968 0.8760 0.000 0.364 0.636
#> GSM907854 3 0.5733 0.8862 0.000 0.324 0.676
#> GSM907855 3 0.5968 0.8760 0.000 0.364 0.636
#> GSM907856 3 0.5968 0.8760 0.000 0.364 0.636
#> GSM907857 3 0.5244 0.7870 0.004 0.240 0.756
#> GSM907825 2 0.5905 0.0923 0.000 0.648 0.352
#> GSM907828 2 0.1643 0.7361 0.000 0.956 0.044
#> GSM907832 2 0.2537 0.7335 0.000 0.920 0.080
#> GSM907833 2 0.2165 0.7426 0.000 0.936 0.064
#> GSM907834 2 0.6026 -0.0186 0.000 0.624 0.376
#> GSM907826 2 0.2878 0.7171 0.000 0.904 0.096
#> GSM907827 2 0.5835 0.1227 0.000 0.660 0.340
#> GSM907829 3 0.8119 0.2912 0.068 0.432 0.500
#> GSM907830 2 0.1964 0.7328 0.000 0.944 0.056
#> GSM907831 2 0.6154 -0.1690 0.000 0.592 0.408
#> GSM907792 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907795 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907801 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907802 1 0.3896 0.8597 0.864 0.008 0.128
#> GSM907804 1 0.2448 0.8793 0.924 0.000 0.076
#> GSM907805 1 0.1031 0.8878 0.976 0.000 0.024
#> GSM907806 1 0.1031 0.8856 0.976 0.000 0.024
#> GSM907793 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907794 1 0.3112 0.8740 0.900 0.004 0.096
#> GSM907796 1 0.3573 0.8637 0.876 0.004 0.120
#> GSM907797 1 0.3573 0.8637 0.876 0.004 0.120
#> GSM907798 1 0.3573 0.8637 0.876 0.004 0.120
#> GSM907799 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907800 1 0.2682 0.8785 0.920 0.004 0.076
#> GSM907803 1 0.4002 0.8852 0.840 0.000 0.160
#> GSM907864 2 0.3690 0.6908 0.016 0.884 0.100
#> GSM907865 2 0.6448 0.3479 0.016 0.656 0.328
#> GSM907868 3 0.5835 0.8923 0.000 0.340 0.660
#> GSM907869 3 0.5244 0.7870 0.004 0.240 0.756
#> GSM907870 2 0.1643 0.7361 0.000 0.956 0.044
#> GSM907861 3 0.5835 0.8923 0.000 0.340 0.660
#> GSM907862 2 0.6305 -0.5857 0.000 0.516 0.484
#> GSM907863 2 0.6299 -0.5635 0.000 0.524 0.476
#> GSM907866 3 0.5678 0.8801 0.000 0.316 0.684
#> GSM907867 3 0.5905 0.8827 0.000 0.352 0.648
#> GSM907839 2 0.3690 0.6908 0.016 0.884 0.100
#> GSM907840 2 0.2860 0.7167 0.004 0.912 0.084
#> GSM907842 2 0.2860 0.7167 0.004 0.912 0.084
#> GSM907843 2 0.2772 0.7175 0.004 0.916 0.080
#> GSM907845 2 0.5365 0.5090 0.004 0.744 0.252
#> GSM907846 2 0.2537 0.7344 0.000 0.920 0.080
#> GSM907848 2 0.2066 0.7437 0.000 0.940 0.060
#> GSM907851 2 0.2774 0.7205 0.008 0.920 0.072
#> GSM907835 2 0.2261 0.7408 0.000 0.932 0.068
#> GSM907836 2 0.2165 0.7423 0.000 0.936 0.064
#> GSM907837 2 0.0237 0.7445 0.000 0.996 0.004
#> GSM907838 2 0.0237 0.7445 0.000 0.996 0.004
#> GSM907841 3 0.5810 0.8922 0.000 0.336 0.664
#> GSM907844 2 0.3816 0.6499 0.000 0.852 0.148
#> GSM907847 2 0.1860 0.7454 0.000 0.948 0.052
#> GSM907849 2 0.2774 0.7205 0.008 0.920 0.072
#> GSM907850 2 0.2066 0.7437 0.000 0.940 0.060
#> GSM907852 2 0.2261 0.7408 0.000 0.932 0.068
#> GSM907853 2 0.2165 0.7426 0.000 0.936 0.064
#> GSM907807 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907813 1 0.5921 0.8231 0.756 0.032 0.212
#> GSM907814 1 0.4399 0.8673 0.812 0.000 0.188
#> GSM907816 1 0.3816 0.8855 0.852 0.000 0.148
#> GSM907818 1 0.3573 0.8652 0.876 0.004 0.120
#> GSM907819 1 0.3644 0.8637 0.872 0.004 0.124
#> GSM907820 1 0.3043 0.8761 0.908 0.008 0.084
#> GSM907822 1 0.3816 0.8855 0.852 0.000 0.148
#> GSM907823 1 0.3816 0.8855 0.852 0.000 0.148
#> GSM907808 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907809 1 0.3752 0.8865 0.856 0.000 0.144
#> GSM907810 1 0.3879 0.8854 0.848 0.000 0.152
#> GSM907811 1 0.4178 0.8841 0.828 0.000 0.172
#> GSM907812 1 0.3038 0.8720 0.896 0.000 0.104
#> GSM907815 1 0.4750 0.7841 0.784 0.000 0.216
#> GSM907817 1 0.2772 0.8778 0.916 0.004 0.080
#> GSM907821 1 0.4033 0.8553 0.856 0.008 0.136
#> GSM907824 1 0.3826 0.8618 0.868 0.008 0.124
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.1211 0.919 0.000 0.040 0.960 0.000
#> GSM907859 2 0.7526 0.285 0.000 0.440 0.188 0.372
#> GSM907860 3 0.1661 0.917 0.000 0.052 0.944 0.004
#> GSM907854 3 0.1398 0.918 0.000 0.040 0.956 0.004
#> GSM907855 3 0.1474 0.918 0.000 0.052 0.948 0.000
#> GSM907856 3 0.1474 0.918 0.000 0.052 0.948 0.000
#> GSM907857 3 0.1191 0.881 0.004 0.004 0.968 0.024
#> GSM907825 2 0.4897 0.511 0.000 0.660 0.332 0.008
#> GSM907828 2 0.3249 0.701 0.000 0.852 0.008 0.140
#> GSM907832 2 0.3718 0.709 0.000 0.820 0.168 0.012
#> GSM907833 2 0.2867 0.736 0.000 0.884 0.104 0.012
#> GSM907834 2 0.5007 0.470 0.000 0.636 0.356 0.008
#> GSM907826 2 0.3539 0.696 0.000 0.820 0.176 0.004
#> GSM907827 2 0.4836 0.529 0.000 0.672 0.320 0.008
#> GSM907829 2 0.8469 0.188 0.188 0.424 0.348 0.040
#> GSM907830 2 0.3718 0.693 0.000 0.820 0.012 0.168
#> GSM907831 2 0.5055 0.440 0.000 0.624 0.368 0.008
#> GSM907792 4 0.4955 0.894 0.444 0.000 0.000 0.556
#> GSM907795 4 0.4933 0.893 0.432 0.000 0.000 0.568
#> GSM907801 4 0.4955 0.894 0.444 0.000 0.000 0.556
#> GSM907802 1 0.1661 0.754 0.944 0.052 0.004 0.000
#> GSM907804 1 0.0188 0.776 0.996 0.000 0.000 0.004
#> GSM907805 1 0.3569 0.532 0.804 0.000 0.000 0.196
#> GSM907806 1 0.0921 0.755 0.972 0.000 0.000 0.028
#> GSM907793 4 0.4933 0.893 0.432 0.000 0.000 0.568
#> GSM907794 1 0.0188 0.776 0.996 0.000 0.000 0.004
#> GSM907796 1 0.3731 0.707 0.844 0.000 0.036 0.120
#> GSM907797 1 0.3999 0.695 0.824 0.000 0.036 0.140
#> GSM907798 1 0.3842 0.700 0.836 0.000 0.036 0.128
#> GSM907799 4 0.4955 0.894 0.444 0.000 0.000 0.556
#> GSM907800 1 0.0188 0.777 0.996 0.004 0.000 0.000
#> GSM907803 1 0.4999 -0.808 0.508 0.000 0.000 0.492
#> GSM907864 2 0.5055 0.565 0.000 0.624 0.008 0.368
#> GSM907865 2 0.7526 0.285 0.000 0.440 0.188 0.372
#> GSM907868 3 0.1302 0.920 0.000 0.044 0.956 0.000
#> GSM907869 3 0.1296 0.879 0.004 0.004 0.964 0.028
#> GSM907870 2 0.3636 0.690 0.000 0.820 0.008 0.172
#> GSM907861 3 0.1576 0.918 0.000 0.048 0.948 0.004
#> GSM907862 3 0.5815 0.559 0.000 0.288 0.652 0.060
#> GSM907863 3 0.5815 0.559 0.000 0.288 0.652 0.060
#> GSM907866 3 0.2021 0.914 0.000 0.040 0.936 0.024
#> GSM907867 3 0.1489 0.919 0.000 0.044 0.952 0.004
#> GSM907839 2 0.5055 0.565 0.000 0.624 0.008 0.368
#> GSM907840 2 0.5055 0.565 0.000 0.624 0.008 0.368
#> GSM907842 2 0.5055 0.565 0.000 0.624 0.008 0.368
#> GSM907843 2 0.3893 0.679 0.000 0.796 0.008 0.196
#> GSM907845 2 0.4601 0.622 0.008 0.732 0.256 0.004
#> GSM907846 2 0.3560 0.724 0.004 0.844 0.140 0.012
#> GSM907848 2 0.2867 0.736 0.000 0.884 0.104 0.012
#> GSM907851 2 0.3448 0.694 0.000 0.828 0.004 0.168
#> GSM907835 2 0.2714 0.730 0.000 0.884 0.112 0.004
#> GSM907836 2 0.2714 0.732 0.000 0.884 0.112 0.004
#> GSM907837 2 0.2670 0.725 0.000 0.908 0.040 0.052
#> GSM907838 2 0.2670 0.725 0.000 0.908 0.040 0.052
#> GSM907841 3 0.2021 0.914 0.000 0.040 0.936 0.024
#> GSM907844 2 0.4122 0.644 0.000 0.760 0.236 0.004
#> GSM907847 2 0.2610 0.737 0.000 0.900 0.088 0.012
#> GSM907849 2 0.3448 0.694 0.000 0.828 0.004 0.168
#> GSM907850 2 0.2867 0.736 0.000 0.884 0.104 0.012
#> GSM907852 2 0.2654 0.732 0.000 0.888 0.108 0.004
#> GSM907853 2 0.2530 0.733 0.000 0.888 0.112 0.000
#> GSM907807 4 0.4933 0.893 0.432 0.000 0.000 0.568
#> GSM907813 4 0.4194 0.534 0.228 0.008 0.000 0.764
#> GSM907814 4 0.4122 0.604 0.236 0.004 0.000 0.760
#> GSM907816 4 0.5155 0.867 0.468 0.004 0.000 0.528
#> GSM907818 1 0.0188 0.777 0.996 0.004 0.000 0.000
#> GSM907819 1 0.0188 0.776 0.996 0.000 0.000 0.004
#> GSM907820 1 0.1661 0.754 0.944 0.052 0.004 0.000
#> GSM907822 4 0.5155 0.867 0.468 0.004 0.000 0.528
#> GSM907823 4 0.5155 0.867 0.468 0.004 0.000 0.528
#> GSM907808 4 0.4933 0.893 0.432 0.000 0.000 0.568
#> GSM907809 4 0.4933 0.893 0.432 0.000 0.000 0.568
#> GSM907810 4 0.4955 0.894 0.444 0.000 0.000 0.556
#> GSM907811 1 0.4967 -0.726 0.548 0.000 0.000 0.452
#> GSM907812 1 0.3842 0.700 0.836 0.000 0.036 0.128
#> GSM907815 1 0.5771 0.577 0.712 0.000 0.144 0.144
#> GSM907817 1 0.0188 0.777 0.996 0.004 0.000 0.000
#> GSM907821 1 0.1661 0.754 0.944 0.052 0.004 0.000
#> GSM907824 1 0.1661 0.754 0.944 0.052 0.004 0.000
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.150 0.8908 0.000 0.056 0.940 0.004 0.000
#> GSM907859 4 0.483 0.7879 0.008 0.168 0.088 0.736 0.000
#> GSM907860 3 0.313 0.8787 0.020 0.088 0.872 0.008 0.012
#> GSM907854 3 0.157 0.8908 0.000 0.060 0.936 0.004 0.000
#> GSM907855 3 0.188 0.8918 0.004 0.052 0.932 0.008 0.004
#> GSM907856 3 0.188 0.8918 0.004 0.052 0.932 0.008 0.004
#> GSM907857 3 0.278 0.8233 0.036 0.004 0.896 0.052 0.012
#> GSM907825 2 0.369 0.6671 0.024 0.824 0.132 0.000 0.020
#> GSM907828 2 0.470 -0.0501 0.020 0.592 0.000 0.388 0.000
#> GSM907832 2 0.251 0.7077 0.004 0.908 0.016 0.056 0.016
#> GSM907833 2 0.201 0.7019 0.004 0.924 0.000 0.056 0.016
#> GSM907834 2 0.364 0.6662 0.024 0.824 0.136 0.000 0.016
#> GSM907826 2 0.270 0.7137 0.044 0.896 0.048 0.000 0.012
#> GSM907827 2 0.364 0.6563 0.028 0.820 0.144 0.004 0.004
#> GSM907829 2 0.807 0.2987 0.020 0.492 0.204 0.172 0.112
#> GSM907830 4 0.492 0.5801 0.008 0.432 0.008 0.548 0.004
#> GSM907831 2 0.393 0.6293 0.036 0.788 0.172 0.000 0.004
#> GSM907792 1 0.256 0.9106 0.856 0.000 0.000 0.000 0.144
#> GSM907795 1 0.247 0.9090 0.864 0.000 0.000 0.000 0.136
#> GSM907801 1 0.256 0.9106 0.856 0.000 0.000 0.000 0.144
#> GSM907802 5 0.166 0.7936 0.036 0.024 0.000 0.000 0.940
#> GSM907804 5 0.193 0.7981 0.072 0.004 0.000 0.004 0.920
#> GSM907805 5 0.475 0.0403 0.488 0.000 0.000 0.016 0.496
#> GSM907806 5 0.207 0.7830 0.092 0.000 0.000 0.004 0.904
#> GSM907793 1 0.263 0.9090 0.860 0.000 0.000 0.004 0.136
#> GSM907794 5 0.161 0.7980 0.072 0.000 0.000 0.000 0.928
#> GSM907796 5 0.654 0.6188 0.128 0.000 0.052 0.216 0.604
#> GSM907797 5 0.688 0.5900 0.152 0.000 0.056 0.228 0.564
#> GSM907798 5 0.675 0.5956 0.152 0.000 0.052 0.216 0.580
#> GSM907799 1 0.272 0.9101 0.852 0.000 0.000 0.004 0.144
#> GSM907800 5 0.164 0.7996 0.064 0.004 0.000 0.000 0.932
#> GSM907803 1 0.355 0.8299 0.760 0.000 0.000 0.004 0.236
#> GSM907864 4 0.396 0.8603 0.008 0.256 0.004 0.732 0.000
#> GSM907865 4 0.494 0.7864 0.012 0.168 0.088 0.732 0.000
#> GSM907868 3 0.246 0.8882 0.016 0.076 0.900 0.000 0.008
#> GSM907869 3 0.285 0.8202 0.036 0.004 0.892 0.056 0.012
#> GSM907870 2 0.519 -0.2128 0.044 0.536 0.000 0.420 0.000
#> GSM907861 3 0.286 0.8780 0.016 0.104 0.872 0.000 0.008
#> GSM907862 3 0.653 0.6028 0.040 0.136 0.640 0.168 0.016
#> GSM907863 3 0.657 0.5948 0.040 0.140 0.636 0.168 0.016
#> GSM907866 3 0.335 0.8739 0.032 0.056 0.872 0.032 0.008
#> GSM907867 3 0.317 0.8747 0.020 0.100 0.864 0.004 0.012
#> GSM907839 4 0.396 0.8603 0.008 0.256 0.004 0.732 0.000
#> GSM907840 4 0.396 0.8603 0.008 0.256 0.004 0.732 0.000
#> GSM907842 4 0.369 0.8568 0.000 0.256 0.004 0.740 0.000
#> GSM907843 4 0.482 0.6158 0.024 0.404 0.000 0.572 0.000
#> GSM907845 2 0.344 0.7092 0.012 0.868 0.044 0.056 0.020
#> GSM907846 2 0.321 0.6807 0.008 0.864 0.000 0.060 0.068
#> GSM907848 2 0.201 0.7019 0.004 0.924 0.000 0.056 0.016
#> GSM907851 2 0.507 -0.2061 0.036 0.544 0.000 0.420 0.000
#> GSM907835 2 0.187 0.7203 0.024 0.936 0.032 0.000 0.008
#> GSM907836 2 0.222 0.7170 0.044 0.920 0.024 0.000 0.012
#> GSM907837 2 0.520 0.5092 0.060 0.736 0.024 0.168 0.012
#> GSM907838 2 0.520 0.5092 0.060 0.736 0.024 0.168 0.012
#> GSM907841 3 0.342 0.8731 0.032 0.060 0.868 0.032 0.008
#> GSM907844 2 0.277 0.7039 0.036 0.884 0.076 0.004 0.000
#> GSM907847 2 0.214 0.7003 0.012 0.920 0.000 0.056 0.012
#> GSM907849 2 0.492 -0.1862 0.028 0.552 0.000 0.420 0.000
#> GSM907850 2 0.203 0.7024 0.020 0.924 0.004 0.052 0.000
#> GSM907852 2 0.207 0.7191 0.044 0.924 0.028 0.000 0.004
#> GSM907853 2 0.204 0.7099 0.004 0.928 0.008 0.048 0.012
#> GSM907807 1 0.247 0.9090 0.864 0.000 0.000 0.000 0.136
#> GSM907813 1 0.433 0.6440 0.716 0.000 0.000 0.252 0.032
#> GSM907814 1 0.302 0.7633 0.848 0.000 0.000 0.132 0.020
#> GSM907816 1 0.309 0.8917 0.816 0.000 0.000 0.004 0.180
#> GSM907818 5 0.198 0.7998 0.064 0.000 0.000 0.016 0.920
#> GSM907819 5 0.177 0.7981 0.072 0.000 0.000 0.004 0.924
#> GSM907820 5 0.175 0.7913 0.036 0.028 0.000 0.000 0.936
#> GSM907822 1 0.309 0.8917 0.816 0.000 0.000 0.004 0.180
#> GSM907823 1 0.285 0.8924 0.828 0.000 0.000 0.000 0.172
#> GSM907808 1 0.247 0.9090 0.864 0.000 0.000 0.000 0.136
#> GSM907809 1 0.247 0.9090 0.864 0.000 0.000 0.000 0.136
#> GSM907810 1 0.256 0.9106 0.856 0.000 0.000 0.000 0.144
#> GSM907811 1 0.438 0.4772 0.572 0.000 0.000 0.004 0.424
#> GSM907812 5 0.675 0.5956 0.152 0.000 0.052 0.216 0.580
#> GSM907815 5 0.800 0.4526 0.120 0.000 0.204 0.248 0.428
#> GSM907817 5 0.164 0.7996 0.064 0.004 0.000 0.000 0.932
#> GSM907821 5 0.166 0.7936 0.036 0.024 0.000 0.000 0.940
#> GSM907824 5 0.166 0.7936 0.036 0.024 0.000 0.000 0.940
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.1321 0.860 0.000 0.020 0.952 0.000 0.004 0.024
#> GSM907859 4 0.1605 0.736 0.000 0.044 0.016 0.936 0.004 0.000
#> GSM907860 3 0.2466 0.847 0.000 0.024 0.896 0.000 0.028 0.052
#> GSM907854 3 0.1624 0.858 0.000 0.020 0.936 0.000 0.004 0.040
#> GSM907855 3 0.1124 0.862 0.000 0.008 0.956 0.000 0.000 0.036
#> GSM907856 3 0.1124 0.862 0.000 0.008 0.956 0.000 0.000 0.036
#> GSM907857 3 0.3154 0.795 0.000 0.000 0.800 0.012 0.004 0.184
#> GSM907825 2 0.3273 0.737 0.000 0.848 0.052 0.000 0.032 0.068
#> GSM907828 2 0.6021 -0.253 0.000 0.448 0.000 0.400 0.024 0.128
#> GSM907832 2 0.3597 0.736 0.000 0.832 0.008 0.032 0.040 0.088
#> GSM907833 2 0.3668 0.735 0.000 0.828 0.008 0.036 0.040 0.088
#> GSM907834 2 0.3158 0.739 0.000 0.856 0.052 0.000 0.032 0.060
#> GSM907826 2 0.2778 0.737 0.000 0.872 0.016 0.000 0.032 0.080
#> GSM907827 2 0.3723 0.698 0.000 0.800 0.096 0.000 0.008 0.096
#> GSM907829 2 0.6420 0.155 0.000 0.432 0.096 0.000 0.076 0.396
#> GSM907830 4 0.4749 0.614 0.000 0.212 0.032 0.708 0.008 0.040
#> GSM907831 2 0.3802 0.701 0.000 0.804 0.084 0.000 0.020 0.092
#> GSM907792 1 0.0881 0.898 0.972 0.000 0.000 0.012 0.008 0.008
#> GSM907795 1 0.0622 0.896 0.980 0.000 0.000 0.012 0.000 0.008
#> GSM907801 1 0.0881 0.898 0.972 0.000 0.000 0.012 0.008 0.008
#> GSM907802 5 0.1958 0.959 0.100 0.004 0.000 0.000 0.896 0.000
#> GSM907804 5 0.2302 0.964 0.120 0.000 0.000 0.008 0.872 0.000
#> GSM907805 1 0.4452 0.346 0.664 0.000 0.000 0.016 0.292 0.028
#> GSM907806 5 0.2623 0.944 0.132 0.000 0.000 0.016 0.852 0.000
#> GSM907793 1 0.0547 0.897 0.980 0.000 0.000 0.020 0.000 0.000
#> GSM907794 5 0.2302 0.962 0.120 0.000 0.000 0.000 0.872 0.008
#> GSM907796 6 0.5310 0.824 0.116 0.000 0.000 0.000 0.348 0.536
#> GSM907797 6 0.5044 0.832 0.096 0.000 0.000 0.000 0.320 0.584
#> GSM907798 6 0.5469 0.841 0.144 0.000 0.000 0.000 0.324 0.532
#> GSM907799 1 0.0717 0.895 0.976 0.000 0.000 0.016 0.008 0.000
#> GSM907800 5 0.2302 0.963 0.120 0.000 0.000 0.008 0.872 0.000
#> GSM907803 1 0.1434 0.871 0.940 0.000 0.000 0.012 0.048 0.000
#> GSM907864 4 0.1267 0.748 0.000 0.060 0.000 0.940 0.000 0.000
#> GSM907865 4 0.1605 0.733 0.000 0.044 0.016 0.936 0.000 0.004
#> GSM907868 3 0.2024 0.863 0.000 0.016 0.920 0.000 0.028 0.036
#> GSM907869 3 0.3221 0.789 0.000 0.000 0.792 0.020 0.000 0.188
#> GSM907870 4 0.6465 0.301 0.000 0.372 0.000 0.428 0.044 0.156
#> GSM907861 3 0.2566 0.853 0.000 0.064 0.888 0.000 0.028 0.020
#> GSM907862 3 0.5857 0.675 0.000 0.084 0.684 0.100 0.044 0.088
#> GSM907863 3 0.5857 0.675 0.000 0.084 0.684 0.100 0.044 0.088
#> GSM907866 3 0.3101 0.824 0.000 0.020 0.832 0.012 0.000 0.136
#> GSM907867 3 0.2545 0.845 0.000 0.028 0.892 0.000 0.028 0.052
#> GSM907839 4 0.1267 0.748 0.000 0.060 0.000 0.940 0.000 0.000
#> GSM907840 4 0.1267 0.748 0.000 0.060 0.000 0.940 0.000 0.000
#> GSM907842 4 0.1882 0.748 0.000 0.060 0.000 0.920 0.012 0.008
#> GSM907843 4 0.5773 0.553 0.000 0.240 0.000 0.592 0.032 0.136
#> GSM907845 2 0.3758 0.741 0.000 0.796 0.012 0.004 0.044 0.144
#> GSM907846 2 0.5012 0.673 0.000 0.724 0.008 0.044 0.128 0.096
#> GSM907848 2 0.3668 0.735 0.000 0.828 0.008 0.036 0.040 0.088
#> GSM907851 4 0.6375 0.290 0.000 0.384 0.000 0.428 0.040 0.148
#> GSM907835 2 0.1755 0.756 0.000 0.932 0.008 0.000 0.032 0.028
#> GSM907836 2 0.2658 0.736 0.000 0.876 0.008 0.000 0.036 0.080
#> GSM907837 2 0.5390 0.583 0.000 0.716 0.040 0.104 0.044 0.096
#> GSM907838 2 0.5433 0.577 0.000 0.712 0.040 0.108 0.044 0.096
#> GSM907841 3 0.3101 0.824 0.000 0.020 0.832 0.012 0.000 0.136
#> GSM907844 2 0.2780 0.738 0.000 0.868 0.024 0.000 0.016 0.092
#> GSM907847 2 0.3503 0.732 0.000 0.836 0.008 0.036 0.028 0.092
#> GSM907849 4 0.6245 0.282 0.000 0.392 0.000 0.432 0.032 0.144
#> GSM907850 2 0.3573 0.717 0.000 0.816 0.000 0.036 0.028 0.120
#> GSM907852 2 0.2532 0.741 0.000 0.884 0.008 0.000 0.032 0.076
#> GSM907853 2 0.2969 0.749 0.000 0.864 0.008 0.012 0.028 0.088
#> GSM907807 1 0.0622 0.896 0.980 0.000 0.000 0.012 0.000 0.008
#> GSM907813 1 0.3648 0.670 0.740 0.004 0.000 0.240 0.000 0.016
#> GSM907814 1 0.2203 0.820 0.896 0.004 0.000 0.084 0.000 0.016
#> GSM907816 1 0.1325 0.890 0.956 0.004 0.000 0.012 0.016 0.012
#> GSM907818 5 0.2618 0.953 0.116 0.000 0.000 0.000 0.860 0.024
#> GSM907819 5 0.2939 0.951 0.120 0.000 0.000 0.016 0.848 0.016
#> GSM907820 5 0.2213 0.949 0.100 0.004 0.000 0.000 0.888 0.008
#> GSM907822 1 0.1223 0.891 0.960 0.004 0.000 0.008 0.016 0.012
#> GSM907823 1 0.1629 0.888 0.940 0.004 0.000 0.004 0.024 0.028
#> GSM907808 1 0.0622 0.896 0.980 0.000 0.000 0.012 0.000 0.008
#> GSM907809 1 0.0622 0.896 0.980 0.000 0.000 0.012 0.000 0.008
#> GSM907810 1 0.0260 0.897 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907811 1 0.3967 0.346 0.632 0.000 0.000 0.012 0.356 0.000
#> GSM907812 6 0.5601 0.840 0.144 0.000 0.000 0.004 0.324 0.528
#> GSM907815 6 0.5529 0.636 0.044 0.000 0.100 0.012 0.172 0.672
#> GSM907817 5 0.2146 0.965 0.116 0.000 0.000 0.004 0.880 0.000
#> GSM907821 5 0.1958 0.959 0.100 0.004 0.000 0.000 0.896 0.000
#> GSM907824 5 0.1958 0.959 0.100 0.004 0.000 0.000 0.896 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
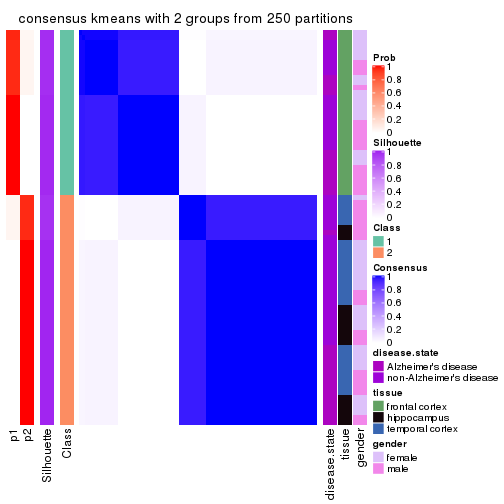
consensus_heatmap(res, k = 3)
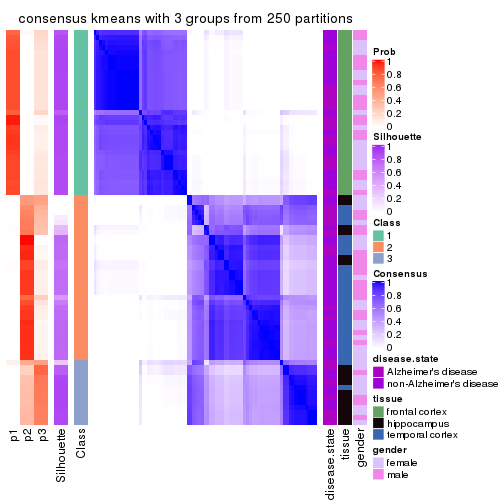
consensus_heatmap(res, k = 4)
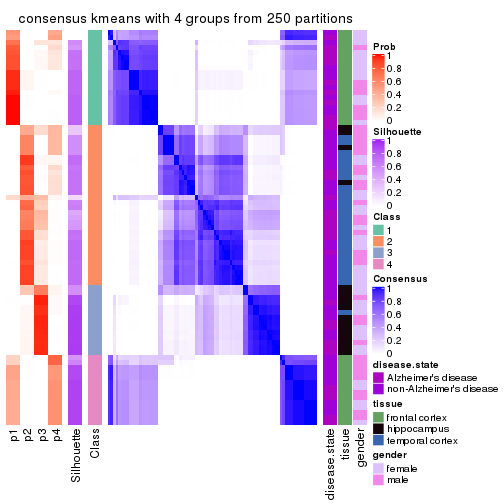
consensus_heatmap(res, k = 5)
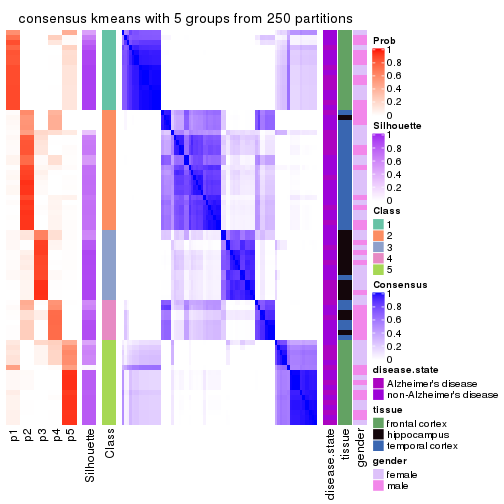
consensus_heatmap(res, k = 6)
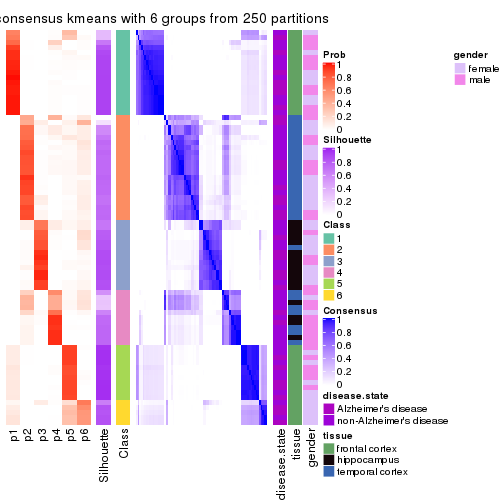
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
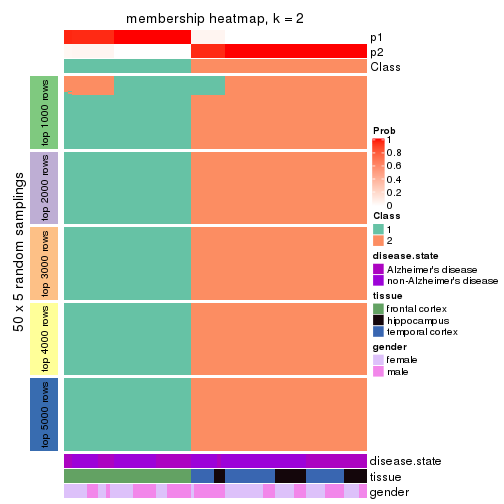
membership_heatmap(res, k = 3)
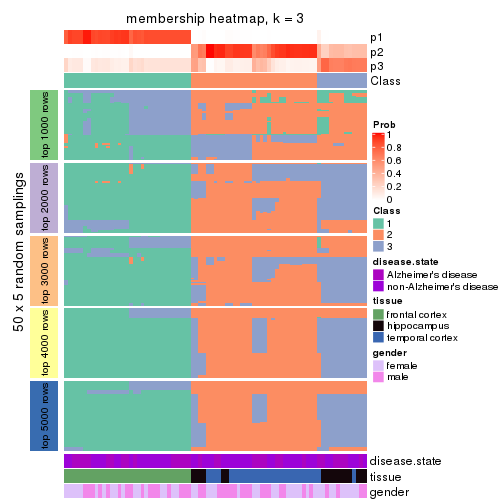
membership_heatmap(res, k = 4)
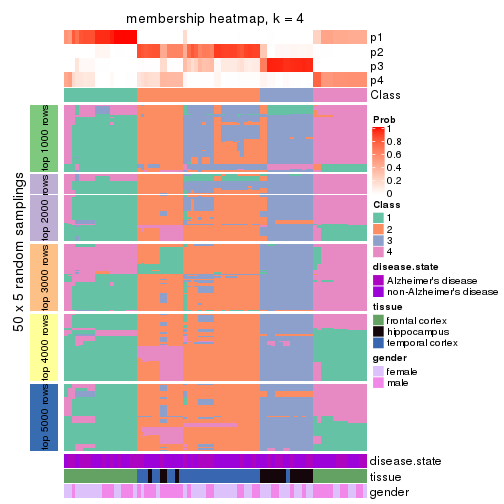
membership_heatmap(res, k = 5)
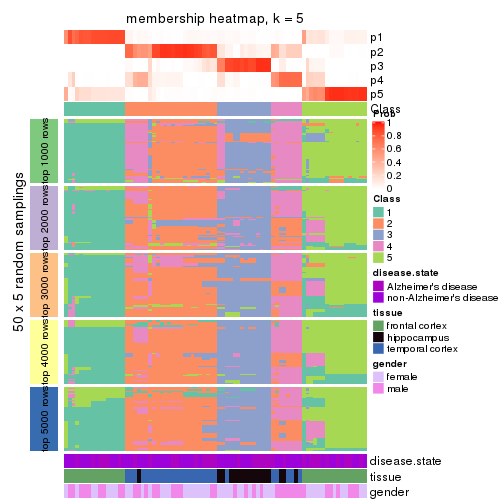
membership_heatmap(res, k = 6)
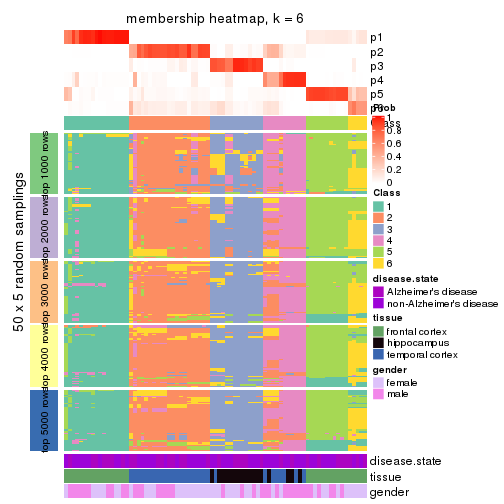
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
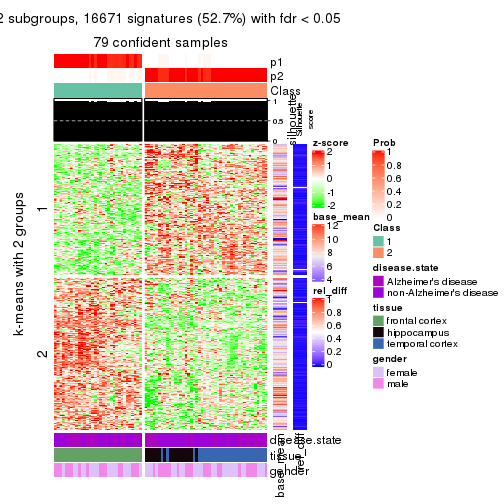
get_signatures(res, k = 3)
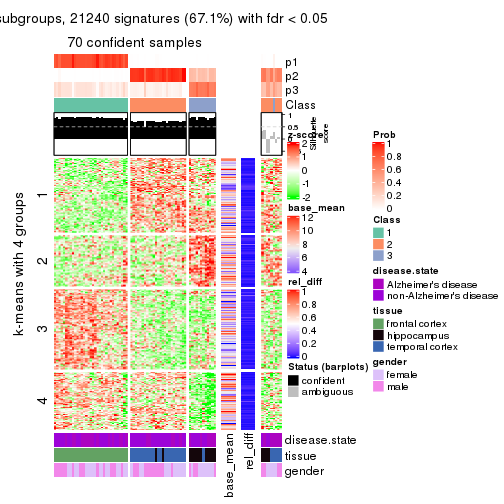
get_signatures(res, k = 4)
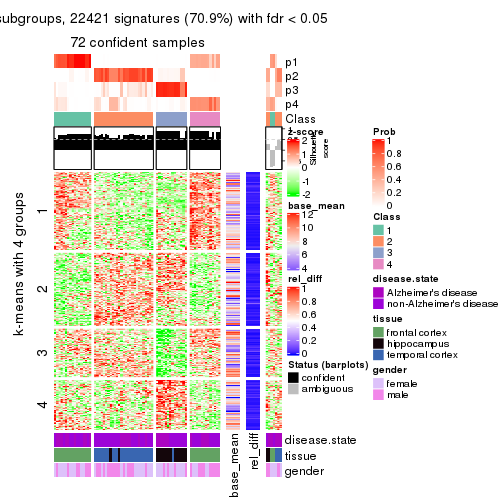
get_signatures(res, k = 5)
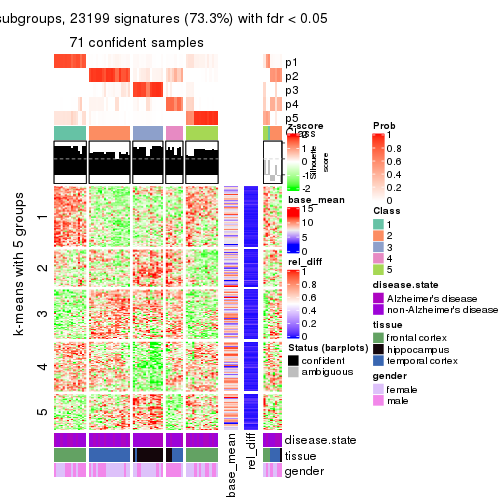
get_signatures(res, k = 6)
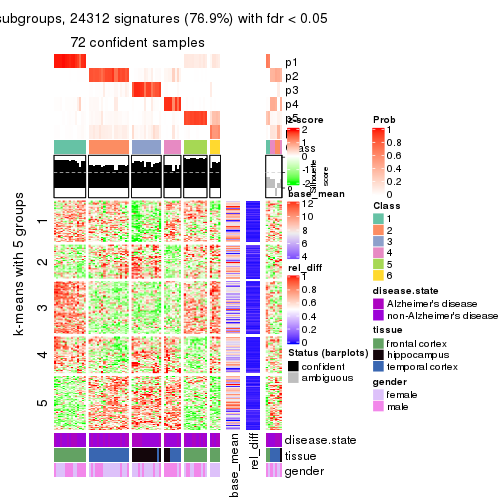
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
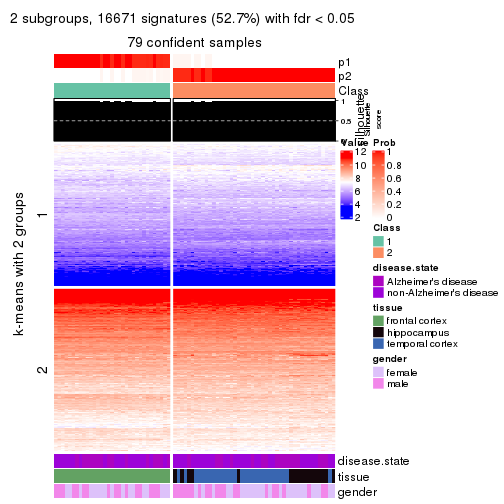
get_signatures(res, k = 3, scale_rows = FALSE)
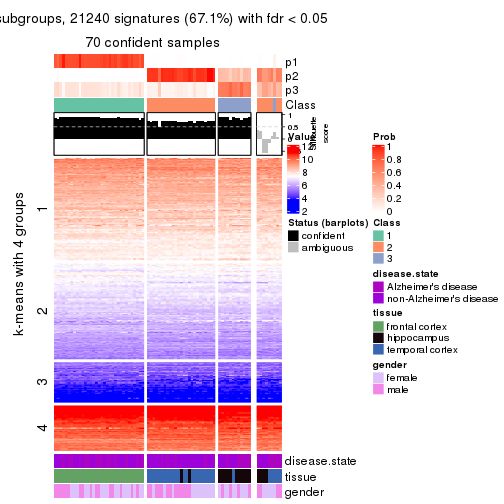
get_signatures(res, k = 4, scale_rows = FALSE)
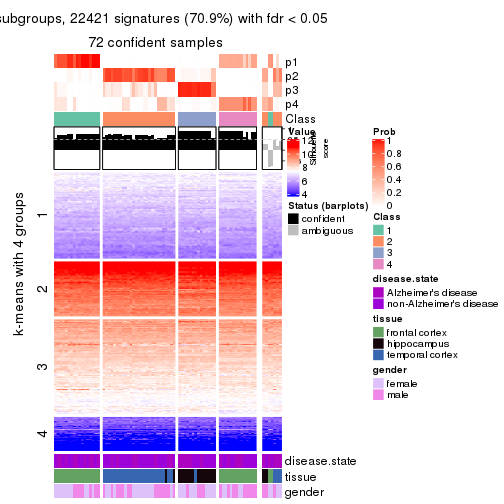
get_signatures(res, k = 5, scale_rows = FALSE)
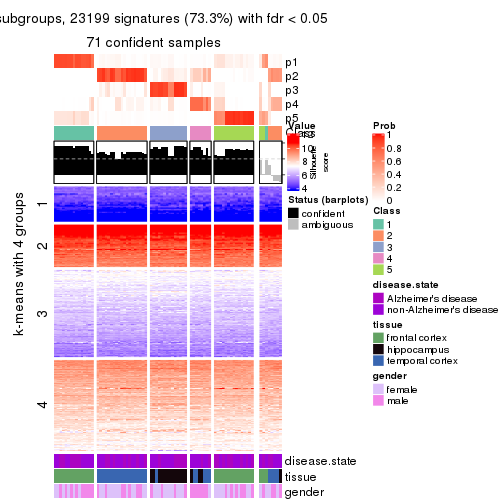
get_signatures(res, k = 6, scale_rows = FALSE)
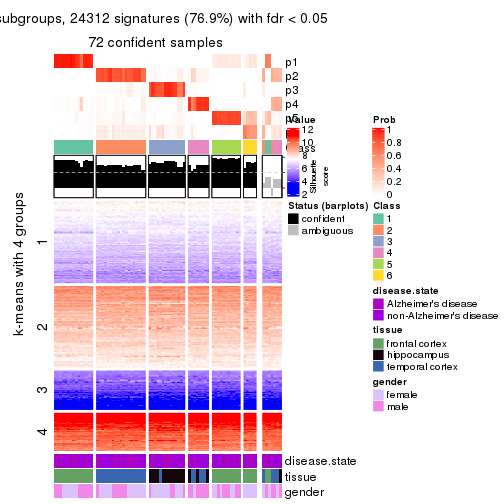
Compare the overlap of signatures from different k:
compare_signatures(res)
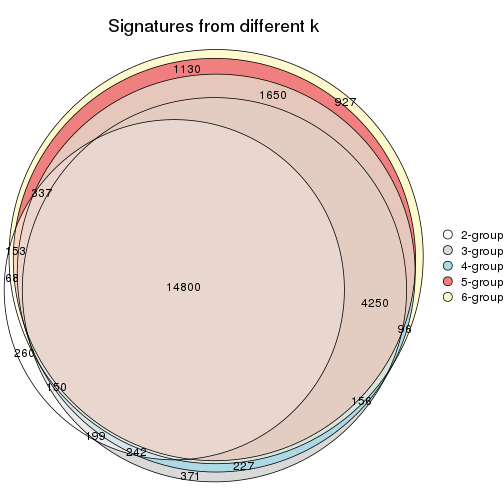
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
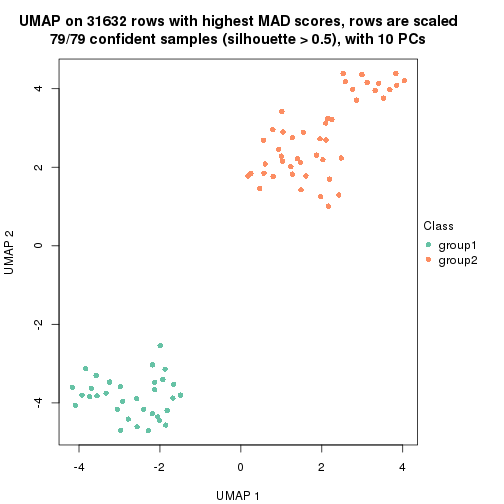
dimension_reduction(res, k = 3, method = "UMAP")
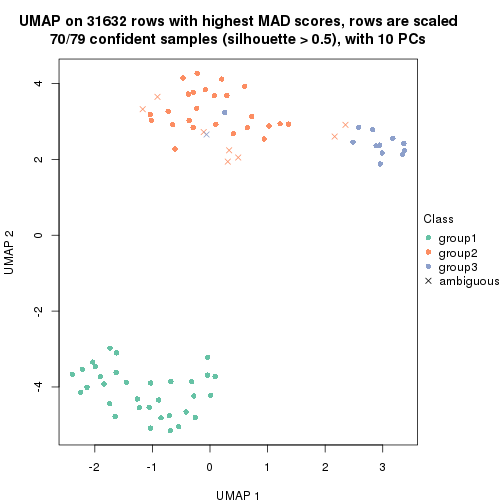
dimension_reduction(res, k = 4, method = "UMAP")
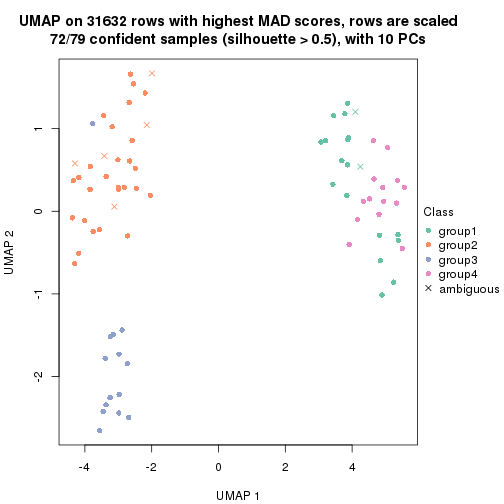
dimension_reduction(res, k = 5, method = "UMAP")
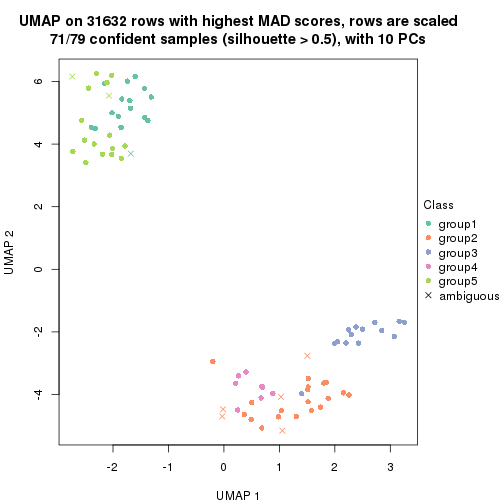
dimension_reduction(res, k = 6, method = "UMAP")
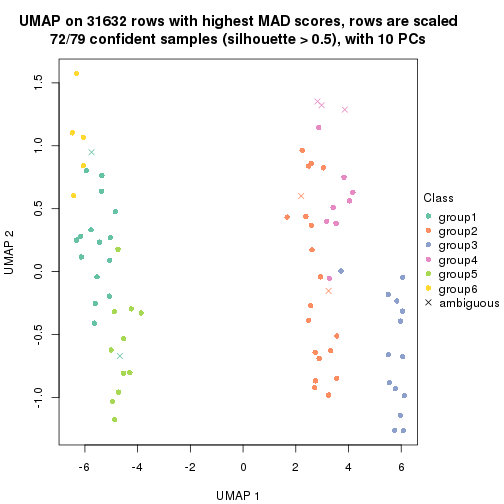
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
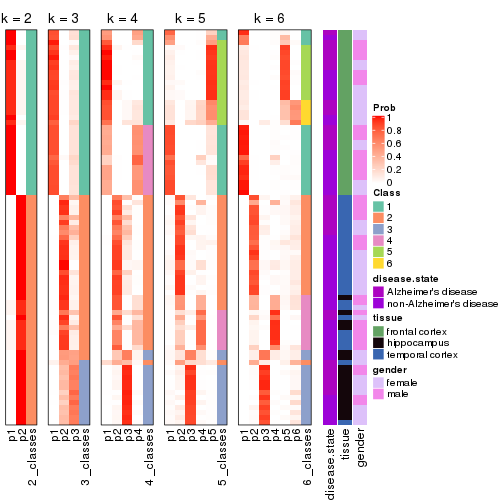
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:kmeans 79 0.5986 7.00e-18 0.9838 2
#> MAD:kmeans 70 0.0832 2.21e-24 0.5546 3
#> MAD:kmeans 72 0.3256 3.90e-24 0.2539 4
#> MAD:kmeans 71 0.7443 1.55e-22 0.0544 5
#> MAD:kmeans 72 0.8708 1.08e-21 0.0178 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "skmeans"]
# you can also extract it by
# res = res_list["MAD:skmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
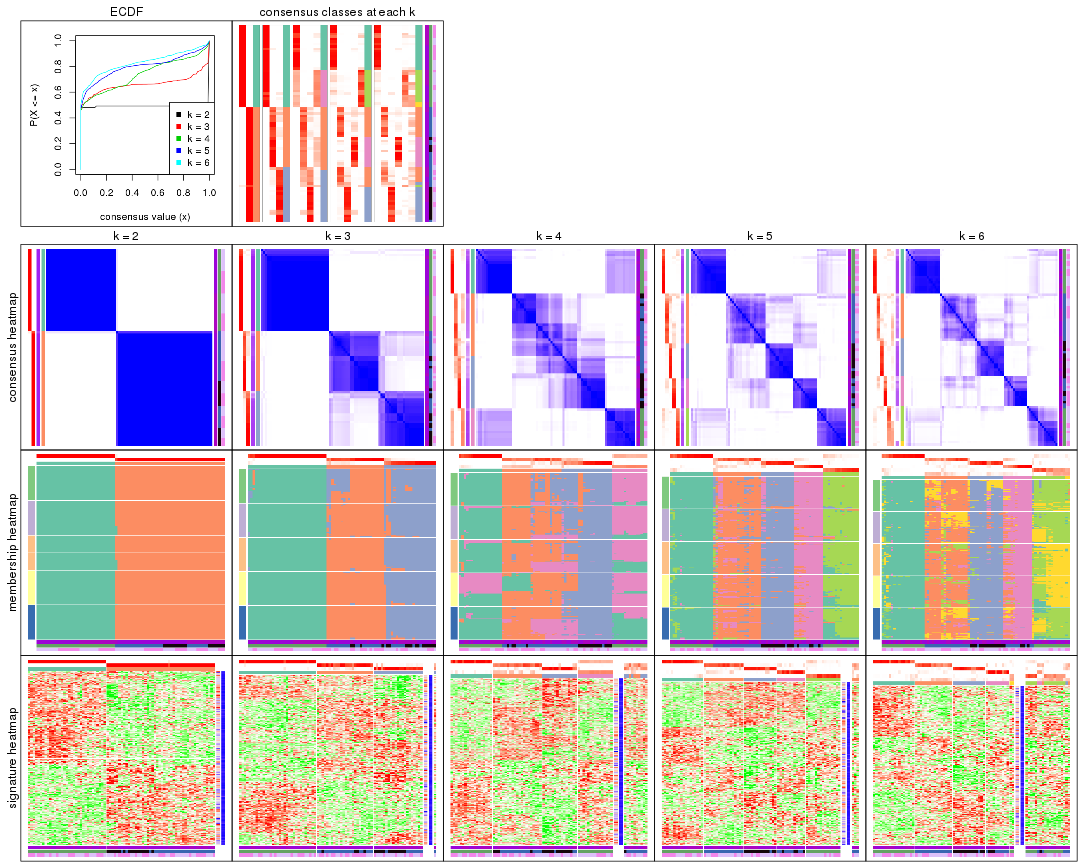
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
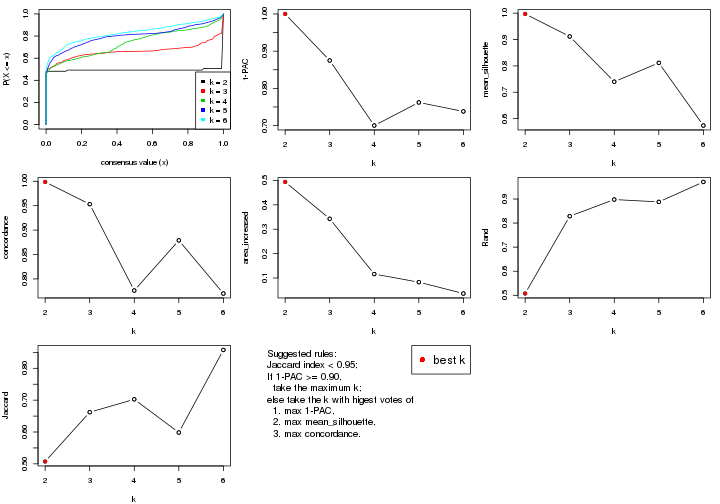
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.997 0.999 0.4936 0.507 0.507
#> 3 3 0.875 0.912 0.953 0.3427 0.829 0.662
#> 4 4 0.700 0.740 0.776 0.1161 0.898 0.703
#> 5 5 0.762 0.811 0.879 0.0829 0.888 0.598
#> 6 6 0.738 0.574 0.770 0.0364 0.971 0.858
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.000 0.998 0.000 1.000
#> GSM907859 2 0.000 0.998 0.000 1.000
#> GSM907860 2 0.000 0.998 0.000 1.000
#> GSM907854 2 0.000 0.998 0.000 1.000
#> GSM907855 2 0.000 0.998 0.000 1.000
#> GSM907856 2 0.000 0.998 0.000 1.000
#> GSM907857 2 0.000 0.998 0.000 1.000
#> GSM907825 2 0.000 0.998 0.000 1.000
#> GSM907828 2 0.000 0.998 0.000 1.000
#> GSM907832 2 0.000 0.998 0.000 1.000
#> GSM907833 2 0.000 0.998 0.000 1.000
#> GSM907834 2 0.000 0.998 0.000 1.000
#> GSM907826 2 0.000 0.998 0.000 1.000
#> GSM907827 2 0.000 0.998 0.000 1.000
#> GSM907829 2 0.506 0.874 0.112 0.888
#> GSM907830 2 0.000 0.998 0.000 1.000
#> GSM907831 2 0.000 0.998 0.000 1.000
#> GSM907792 1 0.000 1.000 1.000 0.000
#> GSM907795 1 0.000 1.000 1.000 0.000
#> GSM907801 1 0.000 1.000 1.000 0.000
#> GSM907802 1 0.000 1.000 1.000 0.000
#> GSM907804 1 0.000 1.000 1.000 0.000
#> GSM907805 1 0.000 1.000 1.000 0.000
#> GSM907806 1 0.000 1.000 1.000 0.000
#> GSM907793 1 0.000 1.000 1.000 0.000
#> GSM907794 1 0.000 1.000 1.000 0.000
#> GSM907796 1 0.000 1.000 1.000 0.000
#> GSM907797 1 0.000 1.000 1.000 0.000
#> GSM907798 1 0.000 1.000 1.000 0.000
#> GSM907799 1 0.000 1.000 1.000 0.000
#> GSM907800 1 0.000 1.000 1.000 0.000
#> GSM907803 1 0.000 1.000 1.000 0.000
#> GSM907864 2 0.000 0.998 0.000 1.000
#> GSM907865 2 0.000 0.998 0.000 1.000
#> GSM907868 2 0.000 0.998 0.000 1.000
#> GSM907869 2 0.000 0.998 0.000 1.000
#> GSM907870 2 0.000 0.998 0.000 1.000
#> GSM907861 2 0.000 0.998 0.000 1.000
#> GSM907862 2 0.000 0.998 0.000 1.000
#> GSM907863 2 0.000 0.998 0.000 1.000
#> GSM907866 2 0.000 0.998 0.000 1.000
#> GSM907867 2 0.000 0.998 0.000 1.000
#> GSM907839 2 0.000 0.998 0.000 1.000
#> GSM907840 2 0.000 0.998 0.000 1.000
#> GSM907842 2 0.000 0.998 0.000 1.000
#> GSM907843 2 0.000 0.998 0.000 1.000
#> GSM907845 2 0.000 0.998 0.000 1.000
#> GSM907846 2 0.000 0.998 0.000 1.000
#> GSM907848 2 0.000 0.998 0.000 1.000
#> GSM907851 2 0.000 0.998 0.000 1.000
#> GSM907835 2 0.000 0.998 0.000 1.000
#> GSM907836 2 0.000 0.998 0.000 1.000
#> GSM907837 2 0.000 0.998 0.000 1.000
#> GSM907838 2 0.000 0.998 0.000 1.000
#> GSM907841 2 0.000 0.998 0.000 1.000
#> GSM907844 2 0.000 0.998 0.000 1.000
#> GSM907847 2 0.000 0.998 0.000 1.000
#> GSM907849 2 0.000 0.998 0.000 1.000
#> GSM907850 2 0.000 0.998 0.000 1.000
#> GSM907852 2 0.000 0.998 0.000 1.000
#> GSM907853 2 0.000 0.998 0.000 1.000
#> GSM907807 1 0.000 1.000 1.000 0.000
#> GSM907813 1 0.000 1.000 1.000 0.000
#> GSM907814 1 0.000 1.000 1.000 0.000
#> GSM907816 1 0.000 1.000 1.000 0.000
#> GSM907818 1 0.000 1.000 1.000 0.000
#> GSM907819 1 0.000 1.000 1.000 0.000
#> GSM907820 1 0.000 1.000 1.000 0.000
#> GSM907822 1 0.000 1.000 1.000 0.000
#> GSM907823 1 0.000 1.000 1.000 0.000
#> GSM907808 1 0.000 1.000 1.000 0.000
#> GSM907809 1 0.000 1.000 1.000 0.000
#> GSM907810 1 0.000 1.000 1.000 0.000
#> GSM907811 1 0.000 1.000 1.000 0.000
#> GSM907812 1 0.000 1.000 1.000 0.000
#> GSM907815 1 0.000 1.000 1.000 0.000
#> GSM907817 1 0.000 1.000 1.000 0.000
#> GSM907821 1 0.000 1.000 1.000 0.000
#> GSM907824 1 0.000 1.000 1.000 0.000
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907859 2 0.1964 0.879 0.000 0.944 0.056
#> GSM907860 3 0.1411 0.903 0.000 0.036 0.964
#> GSM907854 3 0.0237 0.918 0.000 0.004 0.996
#> GSM907855 3 0.1163 0.908 0.000 0.028 0.972
#> GSM907856 3 0.1163 0.908 0.000 0.028 0.972
#> GSM907857 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907825 3 0.1964 0.903 0.000 0.056 0.944
#> GSM907828 2 0.0000 0.910 0.000 1.000 0.000
#> GSM907832 2 0.5058 0.741 0.000 0.756 0.244
#> GSM907833 2 0.3482 0.872 0.000 0.872 0.128
#> GSM907834 3 0.1964 0.903 0.000 0.056 0.944
#> GSM907826 3 0.6095 0.295 0.000 0.392 0.608
#> GSM907827 3 0.2625 0.896 0.000 0.084 0.916
#> GSM907829 3 0.1289 0.913 0.000 0.032 0.968
#> GSM907830 2 0.0237 0.910 0.000 0.996 0.004
#> GSM907831 3 0.1860 0.905 0.000 0.052 0.948
#> GSM907792 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907802 1 0.0237 0.988 0.996 0.000 0.004
#> GSM907804 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907805 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907797 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907798 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907800 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907803 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907864 2 0.0424 0.908 0.000 0.992 0.008
#> GSM907865 2 0.1964 0.879 0.000 0.944 0.056
#> GSM907868 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907869 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907870 2 0.0000 0.910 0.000 1.000 0.000
#> GSM907861 3 0.0237 0.918 0.000 0.004 0.996
#> GSM907862 3 0.5465 0.631 0.000 0.288 0.712
#> GSM907863 3 0.5785 0.553 0.000 0.332 0.668
#> GSM907866 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907867 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907839 2 0.0237 0.910 0.000 0.996 0.004
#> GSM907840 2 0.0237 0.910 0.000 0.996 0.004
#> GSM907842 2 0.0237 0.910 0.000 0.996 0.004
#> GSM907843 2 0.0000 0.910 0.000 1.000 0.000
#> GSM907845 3 0.2261 0.896 0.000 0.068 0.932
#> GSM907846 2 0.5926 0.535 0.000 0.644 0.356
#> GSM907848 2 0.3340 0.877 0.000 0.880 0.120
#> GSM907851 2 0.0000 0.910 0.000 1.000 0.000
#> GSM907835 2 0.3941 0.854 0.000 0.844 0.156
#> GSM907836 2 0.4121 0.842 0.000 0.832 0.168
#> GSM907837 2 0.0424 0.910 0.000 0.992 0.008
#> GSM907838 2 0.0424 0.910 0.000 0.992 0.008
#> GSM907841 3 0.0000 0.919 0.000 0.000 1.000
#> GSM907844 3 0.2959 0.868 0.000 0.100 0.900
#> GSM907847 2 0.2796 0.888 0.000 0.908 0.092
#> GSM907849 2 0.0000 0.910 0.000 1.000 0.000
#> GSM907850 2 0.3482 0.872 0.000 0.872 0.128
#> GSM907852 2 0.3752 0.863 0.000 0.856 0.144
#> GSM907853 2 0.4062 0.845 0.000 0.836 0.164
#> GSM907807 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907813 1 0.2878 0.899 0.904 0.096 0.000
#> GSM907814 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907820 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907822 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907815 1 0.3619 0.849 0.864 0.000 0.136
#> GSM907817 1 0.0000 0.991 1.000 0.000 0.000
#> GSM907821 1 0.1964 0.938 0.944 0.000 0.056
#> GSM907824 1 0.0237 0.988 0.996 0.000 0.004
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0000 0.7897 0.000 0.000 1.000 0.000
#> GSM907859 2 0.6203 0.6462 0.000 0.592 0.068 0.340
#> GSM907860 3 0.1305 0.7701 0.000 0.036 0.960 0.004
#> GSM907854 3 0.0000 0.7897 0.000 0.000 1.000 0.000
#> GSM907855 3 0.0707 0.7819 0.000 0.020 0.980 0.000
#> GSM907856 3 0.0707 0.7819 0.000 0.020 0.980 0.000
#> GSM907857 3 0.0707 0.7829 0.000 0.000 0.980 0.020
#> GSM907825 3 0.5686 0.4952 0.000 0.376 0.592 0.032
#> GSM907828 2 0.4134 0.7149 0.000 0.740 0.000 0.260
#> GSM907832 2 0.4642 0.4623 0.000 0.740 0.240 0.020
#> GSM907833 2 0.3160 0.6318 0.000 0.872 0.108 0.020
#> GSM907834 3 0.5793 0.4812 0.000 0.384 0.580 0.036
#> GSM907826 2 0.5628 -0.0943 0.000 0.556 0.420 0.024
#> GSM907827 3 0.4857 0.6071 0.000 0.284 0.700 0.016
#> GSM907829 3 0.7837 0.3230 0.000 0.292 0.408 0.300
#> GSM907830 2 0.4624 0.6994 0.000 0.660 0.000 0.340
#> GSM907831 3 0.5436 0.5286 0.000 0.356 0.620 0.024
#> GSM907792 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907802 4 0.5040 0.9143 0.364 0.008 0.000 0.628
#> GSM907804 4 0.4916 0.8927 0.424 0.000 0.000 0.576
#> GSM907805 1 0.2589 0.7476 0.884 0.000 0.000 0.116
#> GSM907806 1 0.2345 0.8128 0.900 0.000 0.000 0.100
#> GSM907793 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907794 4 0.4855 0.9200 0.400 0.000 0.000 0.600
#> GSM907796 4 0.4941 0.8925 0.436 0.000 0.000 0.564
#> GSM907797 4 0.5105 0.8928 0.432 0.000 0.004 0.564
#> GSM907798 4 0.4941 0.8925 0.436 0.000 0.000 0.564
#> GSM907799 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907800 4 0.4843 0.9190 0.396 0.000 0.000 0.604
#> GSM907803 1 0.0707 0.9241 0.980 0.000 0.000 0.020
#> GSM907864 2 0.4643 0.6983 0.000 0.656 0.000 0.344
#> GSM907865 2 0.6091 0.6512 0.000 0.596 0.060 0.344
#> GSM907868 3 0.0188 0.7895 0.000 0.000 0.996 0.004
#> GSM907869 3 0.0592 0.7849 0.000 0.000 0.984 0.016
#> GSM907870 2 0.4193 0.7140 0.000 0.732 0.000 0.268
#> GSM907861 3 0.0188 0.7895 0.000 0.000 0.996 0.004
#> GSM907862 3 0.4567 0.5344 0.000 0.244 0.740 0.016
#> GSM907863 3 0.4855 0.4913 0.000 0.268 0.712 0.020
#> GSM907866 3 0.0000 0.7897 0.000 0.000 1.000 0.000
#> GSM907867 3 0.0188 0.7895 0.000 0.000 0.996 0.004
#> GSM907839 2 0.4643 0.6983 0.000 0.656 0.000 0.344
#> GSM907840 2 0.4643 0.6983 0.000 0.656 0.000 0.344
#> GSM907842 2 0.4643 0.6983 0.000 0.656 0.000 0.344
#> GSM907843 2 0.4522 0.7044 0.000 0.680 0.000 0.320
#> GSM907845 3 0.6206 0.4368 0.000 0.404 0.540 0.056
#> GSM907846 2 0.7281 0.3349 0.000 0.532 0.272 0.196
#> GSM907848 2 0.2843 0.6454 0.000 0.892 0.088 0.020
#> GSM907851 2 0.4164 0.7143 0.000 0.736 0.000 0.264
#> GSM907835 2 0.4707 0.4993 0.000 0.760 0.204 0.036
#> GSM907836 2 0.4630 0.5340 0.000 0.768 0.196 0.036
#> GSM907837 2 0.2002 0.6731 0.000 0.936 0.020 0.044
#> GSM907838 2 0.2282 0.6734 0.000 0.924 0.024 0.052
#> GSM907841 3 0.0000 0.7897 0.000 0.000 1.000 0.000
#> GSM907844 3 0.5716 0.4260 0.000 0.420 0.552 0.028
#> GSM907847 2 0.2227 0.6754 0.000 0.928 0.036 0.036
#> GSM907849 2 0.4277 0.7130 0.000 0.720 0.000 0.280
#> GSM907850 2 0.3160 0.6330 0.000 0.872 0.108 0.020
#> GSM907852 2 0.4290 0.5580 0.000 0.800 0.164 0.036
#> GSM907853 2 0.3958 0.5823 0.000 0.824 0.144 0.032
#> GSM907807 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907813 1 0.3591 0.6768 0.824 0.008 0.000 0.168
#> GSM907814 1 0.1867 0.8468 0.928 0.000 0.000 0.072
#> GSM907816 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907818 4 0.4790 0.9213 0.380 0.000 0.000 0.620
#> GSM907819 4 0.4790 0.9213 0.380 0.000 0.000 0.620
#> GSM907820 4 0.5284 0.9091 0.368 0.016 0.000 0.616
#> GSM907822 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.9437 1.000 0.000 0.000 0.000
#> GSM907811 1 0.1557 0.8803 0.944 0.000 0.000 0.056
#> GSM907812 4 0.4955 0.8828 0.444 0.000 0.000 0.556
#> GSM907815 4 0.7082 0.6492 0.252 0.000 0.184 0.564
#> GSM907817 4 0.4843 0.9190 0.396 0.000 0.000 0.604
#> GSM907821 4 0.5127 0.9087 0.356 0.012 0.000 0.632
#> GSM907824 4 0.5237 0.9066 0.356 0.016 0.000 0.628
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0609 0.931 0.000 0.020 0.980 0.000 0.000
#> GSM907859 4 0.0609 0.888 0.000 0.000 0.020 0.980 0.000
#> GSM907860 3 0.1399 0.921 0.000 0.028 0.952 0.020 0.000
#> GSM907854 3 0.0609 0.931 0.000 0.020 0.980 0.000 0.000
#> GSM907855 3 0.0771 0.930 0.000 0.020 0.976 0.004 0.000
#> GSM907856 3 0.0771 0.930 0.000 0.020 0.976 0.004 0.000
#> GSM907857 3 0.0703 0.912 0.000 0.024 0.976 0.000 0.000
#> GSM907825 2 0.2464 0.768 0.000 0.892 0.092 0.004 0.012
#> GSM907828 4 0.3391 0.787 0.000 0.188 0.000 0.800 0.012
#> GSM907832 2 0.3923 0.742 0.000 0.812 0.040 0.132 0.016
#> GSM907833 2 0.3538 0.712 0.000 0.804 0.004 0.176 0.016
#> GSM907834 2 0.2674 0.762 0.000 0.868 0.120 0.000 0.012
#> GSM907826 2 0.2474 0.771 0.000 0.896 0.084 0.012 0.008
#> GSM907827 2 0.4630 0.339 0.000 0.572 0.416 0.008 0.004
#> GSM907829 2 0.7144 0.130 0.008 0.372 0.344 0.004 0.272
#> GSM907830 4 0.1430 0.883 0.000 0.052 0.004 0.944 0.000
#> GSM907831 2 0.3969 0.586 0.000 0.692 0.304 0.000 0.004
#> GSM907792 1 0.0162 0.940 0.996 0.000 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.940 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0162 0.940 0.996 0.000 0.000 0.000 0.004
#> GSM907802 5 0.0794 0.875 0.028 0.000 0.000 0.000 0.972
#> GSM907804 5 0.2424 0.826 0.132 0.000 0.000 0.000 0.868
#> GSM907805 1 0.3197 0.758 0.832 0.012 0.000 0.004 0.152
#> GSM907806 1 0.3707 0.615 0.716 0.000 0.000 0.000 0.284
#> GSM907793 1 0.0000 0.940 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.2536 0.859 0.128 0.000 0.004 0.000 0.868
#> GSM907796 5 0.4693 0.793 0.212 0.044 0.008 0.004 0.732
#> GSM907797 5 0.5046 0.791 0.208 0.044 0.024 0.004 0.720
#> GSM907798 5 0.4972 0.755 0.252 0.044 0.008 0.004 0.692
#> GSM907799 1 0.0671 0.936 0.980 0.004 0.000 0.000 0.016
#> GSM907800 5 0.1282 0.876 0.044 0.004 0.000 0.000 0.952
#> GSM907803 1 0.1410 0.905 0.940 0.000 0.000 0.000 0.060
#> GSM907864 4 0.0162 0.899 0.000 0.004 0.000 0.996 0.000
#> GSM907865 4 0.0404 0.893 0.000 0.000 0.012 0.988 0.000
#> GSM907868 3 0.0510 0.930 0.000 0.016 0.984 0.000 0.000
#> GSM907869 3 0.0703 0.912 0.000 0.024 0.976 0.000 0.000
#> GSM907870 4 0.3621 0.785 0.000 0.192 0.000 0.788 0.020
#> GSM907861 3 0.1341 0.914 0.000 0.056 0.944 0.000 0.000
#> GSM907862 3 0.4674 0.657 0.000 0.060 0.708 0.232 0.000
#> GSM907863 3 0.4755 0.638 0.000 0.060 0.696 0.244 0.000
#> GSM907866 3 0.0404 0.929 0.000 0.012 0.988 0.000 0.000
#> GSM907867 3 0.1484 0.915 0.000 0.048 0.944 0.008 0.000
#> GSM907839 4 0.0162 0.899 0.000 0.004 0.000 0.996 0.000
#> GSM907840 4 0.0162 0.899 0.000 0.004 0.000 0.996 0.000
#> GSM907842 4 0.0162 0.899 0.000 0.004 0.000 0.996 0.000
#> GSM907843 4 0.1942 0.882 0.000 0.068 0.000 0.920 0.012
#> GSM907845 2 0.3722 0.735 0.000 0.824 0.128 0.016 0.032
#> GSM907846 2 0.7971 0.340 0.000 0.448 0.148 0.236 0.168
#> GSM907848 2 0.3461 0.718 0.000 0.812 0.004 0.168 0.016
#> GSM907851 4 0.3882 0.730 0.000 0.224 0.000 0.756 0.020
#> GSM907835 2 0.1310 0.768 0.000 0.956 0.024 0.020 0.000
#> GSM907836 2 0.3461 0.764 0.000 0.848 0.076 0.068 0.008
#> GSM907837 2 0.4128 0.630 0.000 0.752 0.020 0.220 0.008
#> GSM907838 2 0.4524 0.535 0.000 0.692 0.020 0.280 0.008
#> GSM907841 3 0.0404 0.929 0.000 0.012 0.988 0.000 0.000
#> GSM907844 2 0.3001 0.752 0.000 0.844 0.144 0.008 0.004
#> GSM907847 2 0.3690 0.657 0.000 0.764 0.000 0.224 0.012
#> GSM907849 4 0.2997 0.831 0.000 0.148 0.000 0.840 0.012
#> GSM907850 2 0.3461 0.717 0.000 0.812 0.004 0.168 0.016
#> GSM907852 2 0.1617 0.768 0.000 0.948 0.020 0.020 0.012
#> GSM907853 2 0.2414 0.758 0.000 0.900 0.012 0.080 0.008
#> GSM907807 1 0.0000 0.940 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.2249 0.866 0.896 0.000 0.000 0.096 0.008
#> GSM907814 1 0.0703 0.924 0.976 0.000 0.000 0.024 0.000
#> GSM907816 1 0.0404 0.939 0.988 0.000 0.000 0.000 0.012
#> GSM907818 5 0.1917 0.876 0.036 0.016 0.008 0.004 0.936
#> GSM907819 5 0.2228 0.875 0.076 0.012 0.004 0.000 0.908
#> GSM907820 5 0.1918 0.859 0.036 0.036 0.000 0.000 0.928
#> GSM907822 1 0.0290 0.940 0.992 0.000 0.000 0.000 0.008
#> GSM907823 1 0.0404 0.939 0.988 0.000 0.000 0.000 0.012
#> GSM907808 1 0.0000 0.940 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.940 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0162 0.940 0.996 0.000 0.000 0.000 0.004
#> GSM907811 1 0.3210 0.735 0.788 0.000 0.000 0.000 0.212
#> GSM907812 5 0.5308 0.663 0.316 0.044 0.008 0.004 0.628
#> GSM907815 5 0.6155 0.751 0.188 0.044 0.108 0.004 0.656
#> GSM907817 5 0.1124 0.876 0.036 0.004 0.000 0.000 0.960
#> GSM907821 5 0.0703 0.873 0.024 0.000 0.000 0.000 0.976
#> GSM907824 5 0.0794 0.875 0.028 0.000 0.000 0.000 0.972
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0146 0.867 0.000 0.000 0.996 0.000 0.004 0.000
#> GSM907859 4 0.0146 0.810 0.000 0.000 0.004 0.996 0.000 0.000
#> GSM907860 3 0.2062 0.852 0.000 0.004 0.900 0.008 0.000 0.088
#> GSM907854 3 0.0260 0.867 0.000 0.000 0.992 0.000 0.000 0.008
#> GSM907855 3 0.0937 0.867 0.000 0.000 0.960 0.000 0.000 0.040
#> GSM907856 3 0.0937 0.867 0.000 0.000 0.960 0.000 0.000 0.040
#> GSM907857 3 0.2009 0.834 0.000 0.000 0.908 0.000 0.068 0.024
#> GSM907825 2 0.4525 0.697 0.000 0.700 0.072 0.000 0.008 0.220
#> GSM907828 4 0.4707 0.614 0.000 0.216 0.000 0.672 0.000 0.112
#> GSM907832 2 0.2295 0.672 0.000 0.904 0.016 0.052 0.000 0.028
#> GSM907833 2 0.2122 0.661 0.000 0.900 0.000 0.076 0.000 0.024
#> GSM907834 2 0.3886 0.691 0.000 0.776 0.080 0.000 0.004 0.140
#> GSM907826 2 0.4640 0.687 0.000 0.604 0.044 0.004 0.000 0.348
#> GSM907827 3 0.6349 -0.219 0.000 0.332 0.368 0.004 0.004 0.292
#> GSM907829 5 0.6775 0.147 0.000 0.128 0.208 0.000 0.516 0.148
#> GSM907830 4 0.2340 0.764 0.000 0.044 0.004 0.896 0.000 0.056
#> GSM907831 2 0.6035 0.494 0.000 0.460 0.236 0.000 0.004 0.300
#> GSM907792 1 0.0260 0.927 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907795 1 0.0363 0.926 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907801 1 0.0000 0.927 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.4392 -0.718 0.016 0.004 0.000 0.000 0.504 0.476
#> GSM907804 6 0.5322 0.687 0.104 0.000 0.000 0.000 0.424 0.472
#> GSM907805 1 0.3426 0.617 0.720 0.000 0.000 0.000 0.276 0.004
#> GSM907806 1 0.4798 0.515 0.672 0.000 0.000 0.000 0.172 0.156
#> GSM907793 1 0.0547 0.923 0.980 0.000 0.000 0.000 0.020 0.000
#> GSM907794 5 0.5173 -0.430 0.108 0.000 0.000 0.000 0.568 0.324
#> GSM907796 5 0.2006 0.328 0.104 0.000 0.000 0.000 0.892 0.004
#> GSM907797 5 0.2255 0.333 0.088 0.000 0.016 0.000 0.892 0.004
#> GSM907798 5 0.2340 0.325 0.148 0.000 0.000 0.000 0.852 0.000
#> GSM907799 1 0.0458 0.925 0.984 0.000 0.000 0.000 0.016 0.000
#> GSM907800 5 0.4331 -0.705 0.020 0.000 0.000 0.000 0.516 0.464
#> GSM907803 1 0.1930 0.872 0.916 0.000 0.000 0.000 0.048 0.036
#> GSM907864 4 0.0000 0.811 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0146 0.810 0.000 0.000 0.004 0.996 0.000 0.000
#> GSM907868 3 0.0713 0.869 0.000 0.000 0.972 0.000 0.000 0.028
#> GSM907869 3 0.2088 0.834 0.000 0.000 0.904 0.000 0.068 0.028
#> GSM907870 4 0.5627 0.425 0.000 0.304 0.004 0.536 0.000 0.156
#> GSM907861 3 0.1644 0.858 0.000 0.004 0.920 0.000 0.000 0.076
#> GSM907862 3 0.4893 0.666 0.000 0.008 0.668 0.104 0.000 0.220
#> GSM907863 3 0.4961 0.668 0.000 0.008 0.668 0.124 0.000 0.200
#> GSM907866 3 0.1088 0.859 0.000 0.000 0.960 0.000 0.016 0.024
#> GSM907867 3 0.1908 0.850 0.000 0.004 0.900 0.000 0.000 0.096
#> GSM907839 4 0.0000 0.811 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907840 4 0.0000 0.811 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.0146 0.811 0.000 0.000 0.000 0.996 0.000 0.004
#> GSM907843 4 0.3098 0.740 0.000 0.164 0.000 0.812 0.000 0.024
#> GSM907845 2 0.5047 0.542 0.000 0.680 0.036 0.000 0.208 0.076
#> GSM907846 2 0.7823 0.278 0.000 0.396 0.096 0.136 0.064 0.308
#> GSM907848 2 0.1563 0.673 0.000 0.932 0.000 0.056 0.000 0.012
#> GSM907851 4 0.5471 0.367 0.004 0.380 0.000 0.504 0.000 0.112
#> GSM907835 2 0.2912 0.723 0.000 0.784 0.000 0.000 0.000 0.216
#> GSM907836 2 0.4760 0.679 0.000 0.612 0.036 0.016 0.000 0.336
#> GSM907837 2 0.5226 0.616 0.000 0.536 0.008 0.076 0.000 0.380
#> GSM907838 2 0.5838 0.555 0.000 0.492 0.016 0.128 0.000 0.364
#> GSM907841 3 0.1722 0.854 0.000 0.004 0.936 0.008 0.016 0.036
#> GSM907844 2 0.5077 0.668 0.000 0.564 0.092 0.000 0.000 0.344
#> GSM907847 2 0.2651 0.616 0.000 0.860 0.000 0.112 0.000 0.028
#> GSM907849 4 0.4854 0.576 0.000 0.292 0.000 0.620 0.000 0.088
#> GSM907850 2 0.3213 0.688 0.000 0.820 0.000 0.048 0.000 0.132
#> GSM907852 2 0.3772 0.700 0.000 0.672 0.004 0.004 0.000 0.320
#> GSM907853 2 0.1511 0.703 0.000 0.940 0.000 0.012 0.004 0.044
#> GSM907807 1 0.0260 0.926 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907813 1 0.1957 0.842 0.888 0.000 0.000 0.112 0.000 0.000
#> GSM907814 1 0.0260 0.924 0.992 0.000 0.000 0.008 0.000 0.000
#> GSM907816 1 0.0000 0.927 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.3835 -0.304 0.016 0.000 0.000 0.000 0.684 0.300
#> GSM907819 5 0.4294 -0.192 0.048 0.000 0.000 0.000 0.672 0.280
#> GSM907820 6 0.5218 0.670 0.020 0.048 0.000 0.000 0.448 0.484
#> GSM907822 1 0.0000 0.927 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0146 0.926 0.996 0.000 0.000 0.000 0.000 0.004
#> GSM907808 1 0.0458 0.925 0.984 0.000 0.000 0.000 0.016 0.000
#> GSM907809 1 0.0458 0.925 0.984 0.000 0.000 0.000 0.016 0.000
#> GSM907810 1 0.0000 0.927 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.4108 0.659 0.744 0.000 0.000 0.000 0.092 0.164
#> GSM907812 5 0.2730 0.304 0.192 0.000 0.000 0.000 0.808 0.000
#> GSM907815 5 0.4208 0.290 0.064 0.000 0.140 0.000 0.768 0.028
#> GSM907817 5 0.4403 -0.718 0.024 0.000 0.000 0.000 0.508 0.468
#> GSM907821 5 0.4212 -0.617 0.016 0.000 0.000 0.000 0.560 0.424
#> GSM907824 5 0.4258 -0.697 0.016 0.000 0.000 0.000 0.516 0.468
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
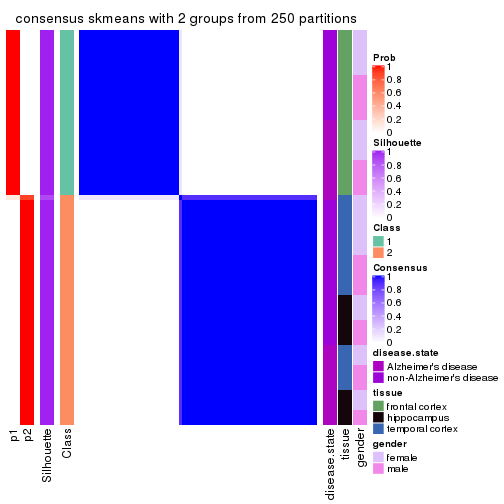
consensus_heatmap(res, k = 3)
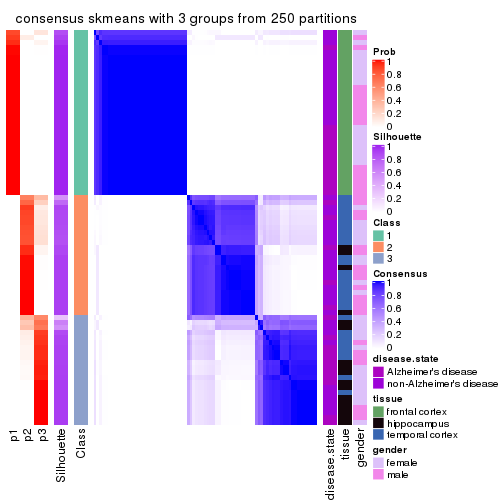
consensus_heatmap(res, k = 4)
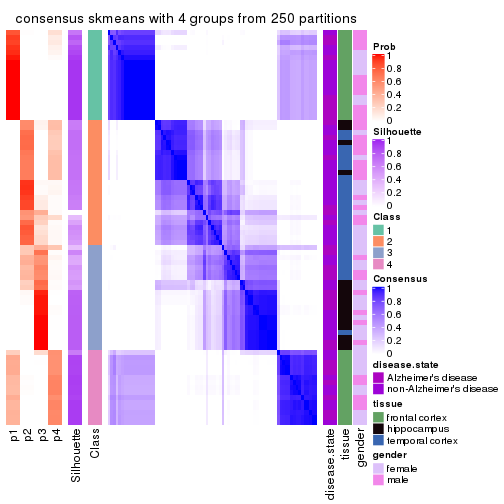
consensus_heatmap(res, k = 5)
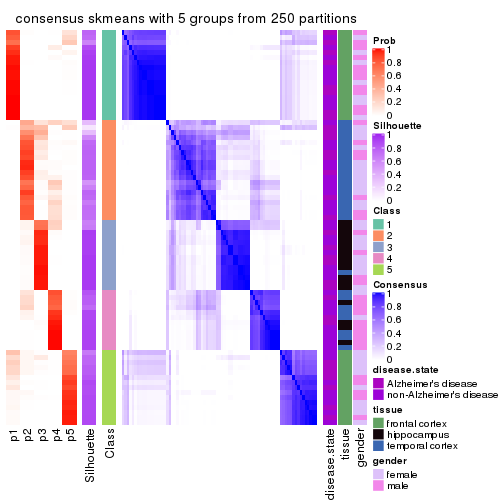
consensus_heatmap(res, k = 6)
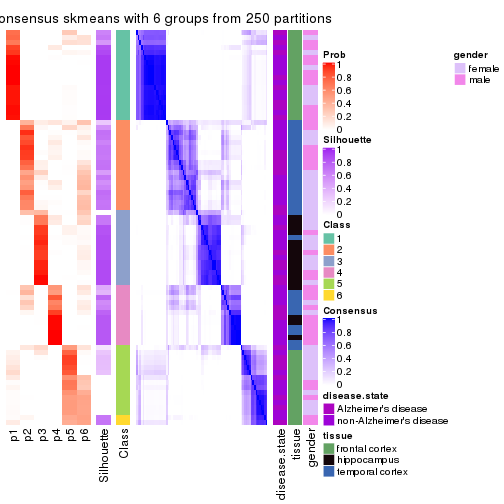
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
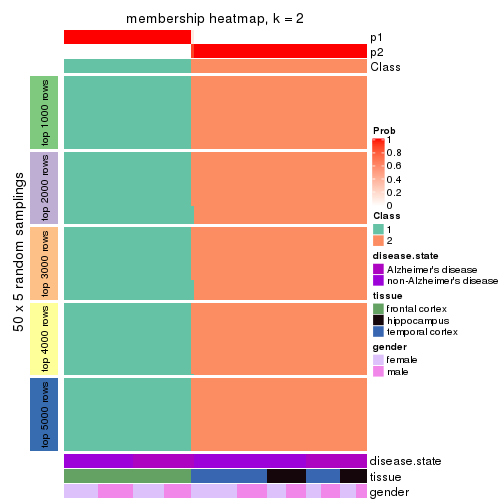
membership_heatmap(res, k = 3)
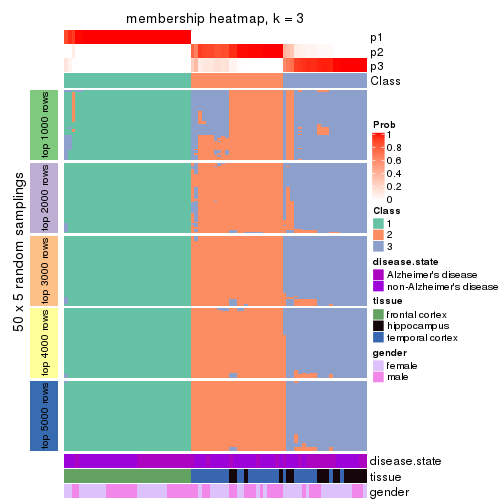
membership_heatmap(res, k = 4)
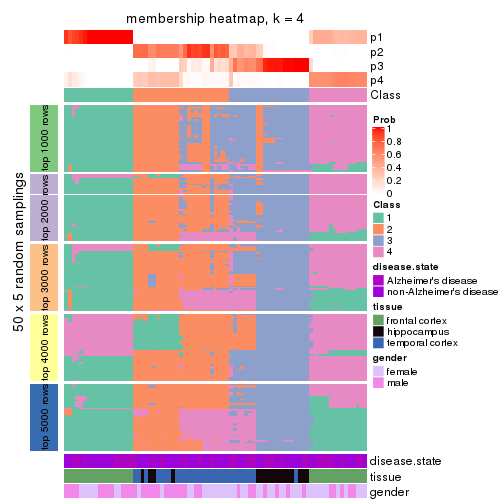
membership_heatmap(res, k = 5)
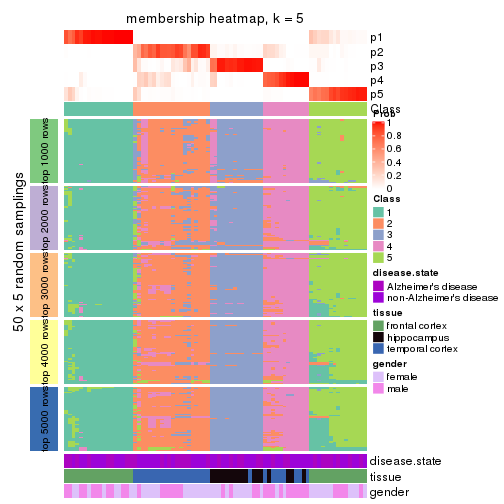
membership_heatmap(res, k = 6)
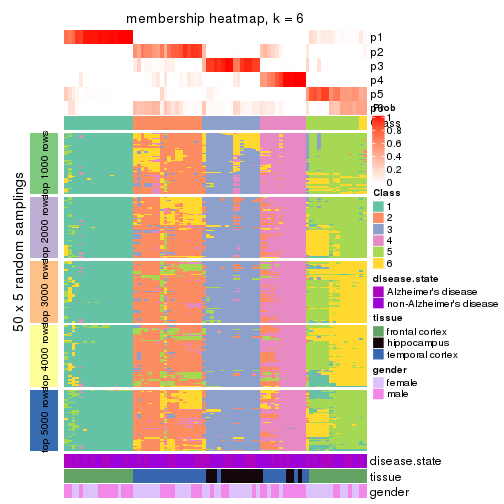
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
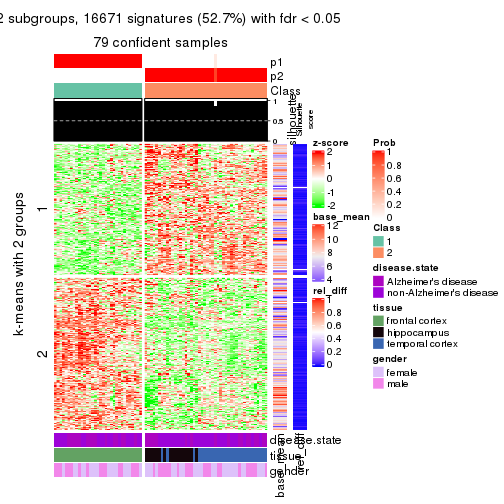
get_signatures(res, k = 3)
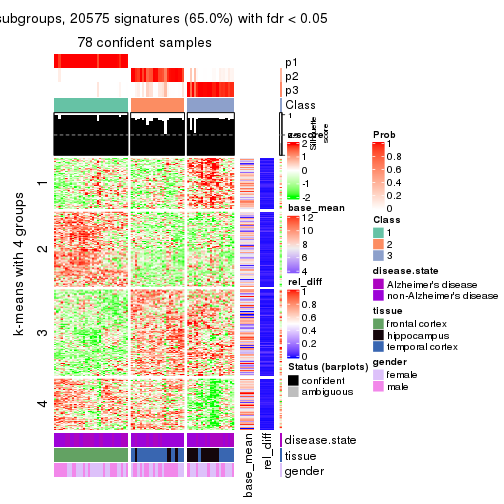
get_signatures(res, k = 4)
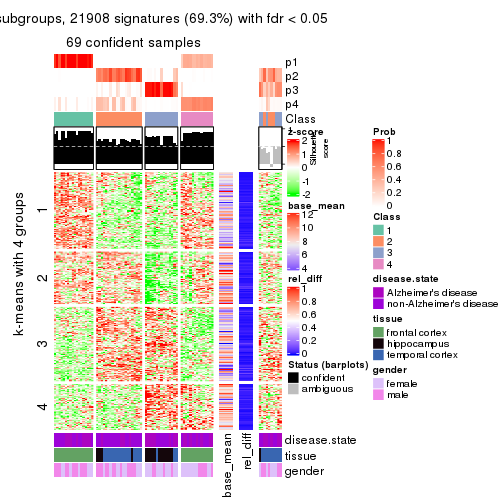
get_signatures(res, k = 5)
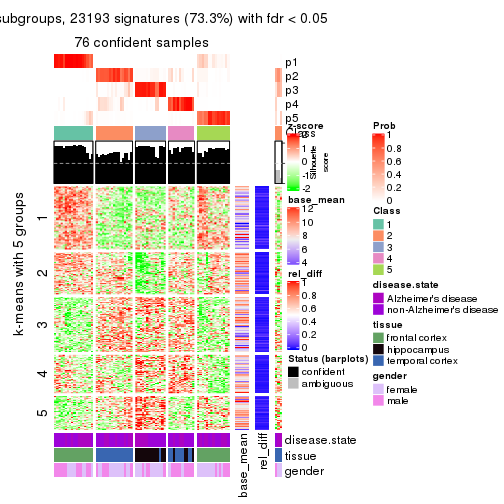
get_signatures(res, k = 6)
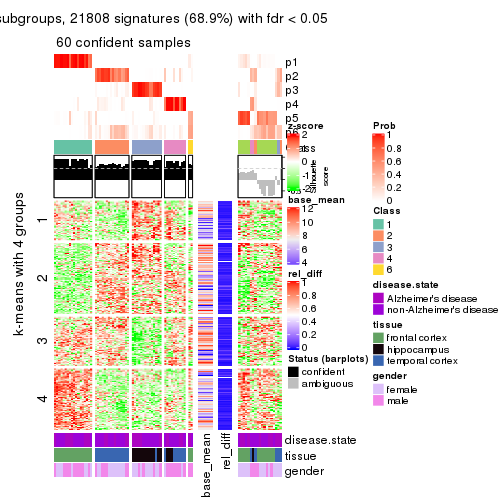
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
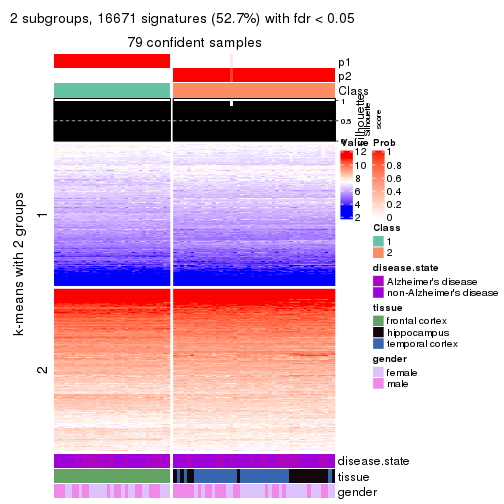
get_signatures(res, k = 3, scale_rows = FALSE)
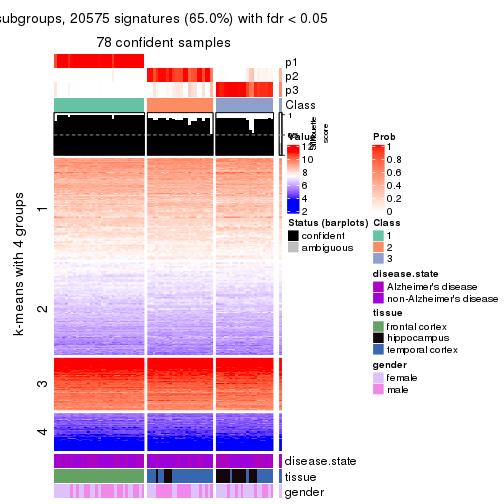
get_signatures(res, k = 4, scale_rows = FALSE)
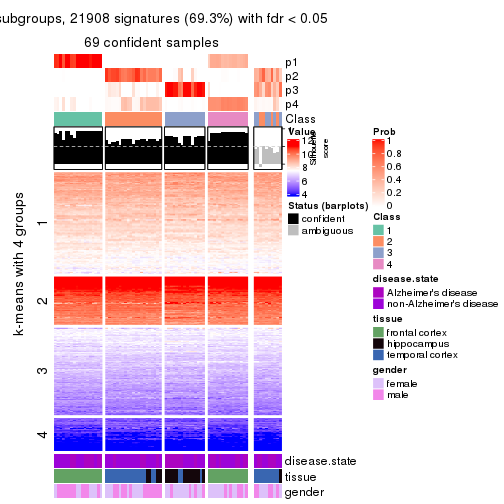
get_signatures(res, k = 5, scale_rows = FALSE)
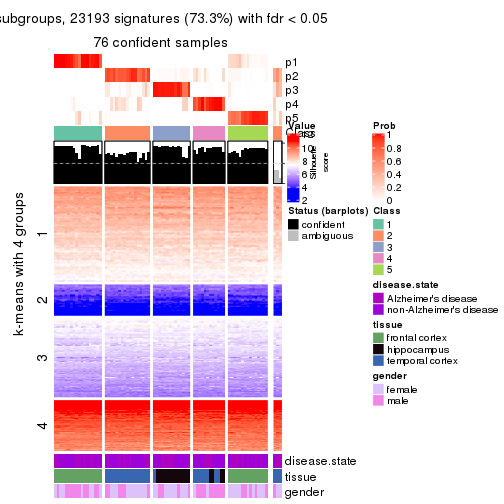
get_signatures(res, k = 6, scale_rows = FALSE)
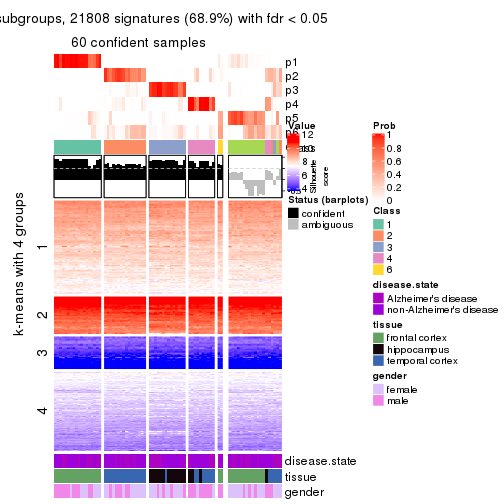
Compare the overlap of signatures from different k:
compare_signatures(res)
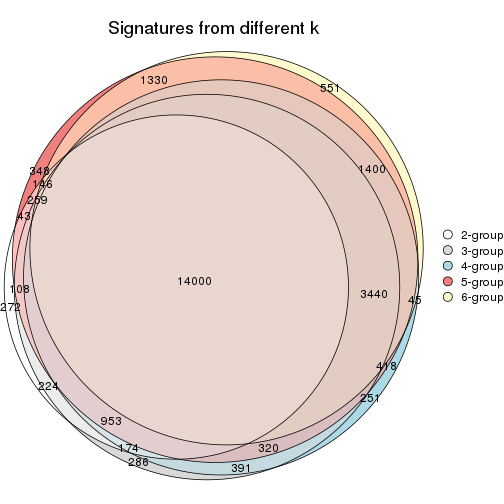
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
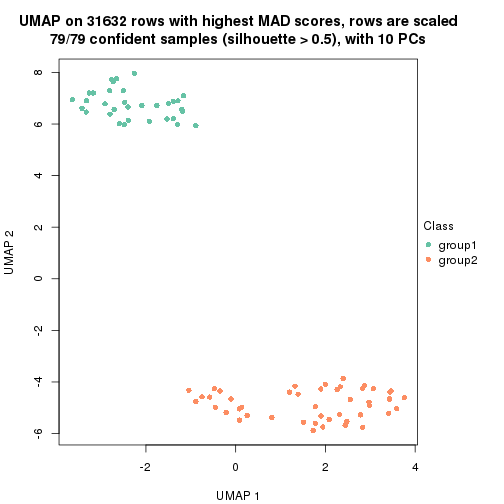
dimension_reduction(res, k = 3, method = "UMAP")
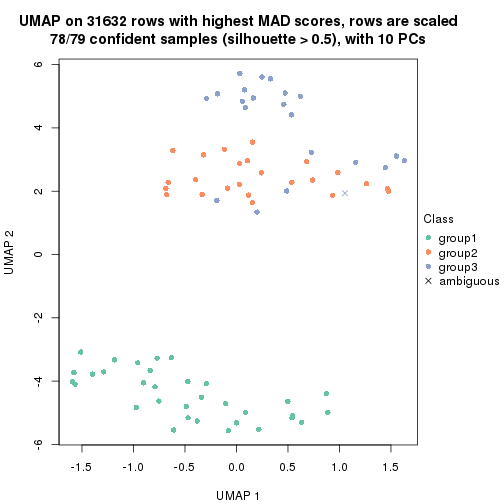
dimension_reduction(res, k = 4, method = "UMAP")
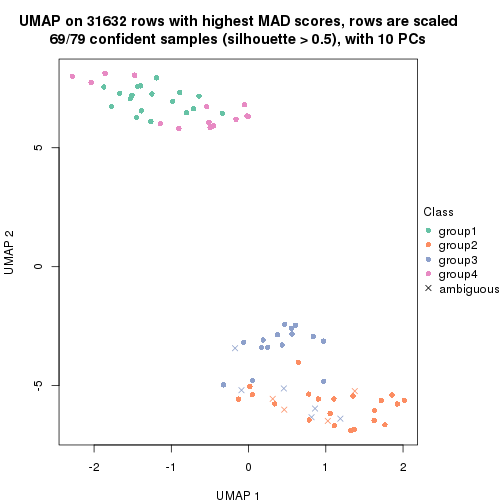
dimension_reduction(res, k = 5, method = "UMAP")
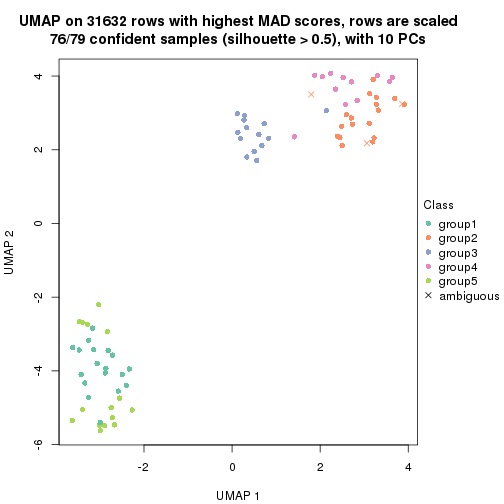
dimension_reduction(res, k = 6, method = "UMAP")
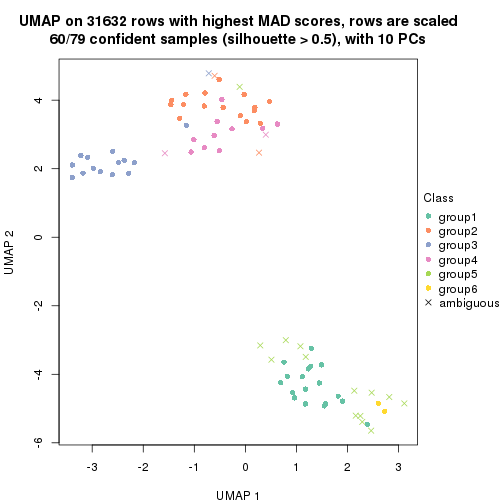
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
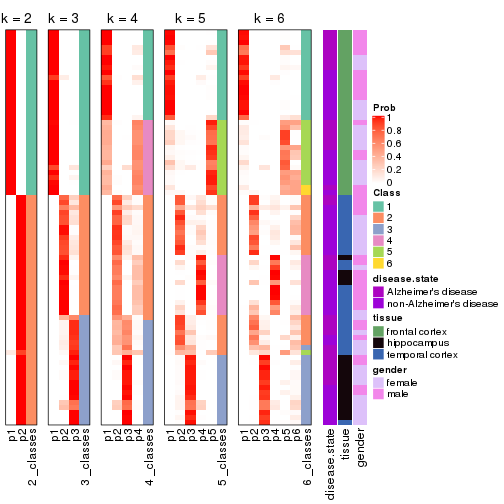
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:skmeans 79 0.5986 7.00e-18 0.9838 2
#> MAD:skmeans 78 0.0661 1.20e-19 0.2426 3
#> MAD:skmeans 69 0.1449 3.99e-18 0.1156 4
#> MAD:skmeans 76 0.7808 2.52e-23 0.0193 5
#> MAD:skmeans 60 0.8856 2.58e-18 0.0403 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "pam"]
# you can also extract it by
# res = res_list["MAD:pam"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'pam' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
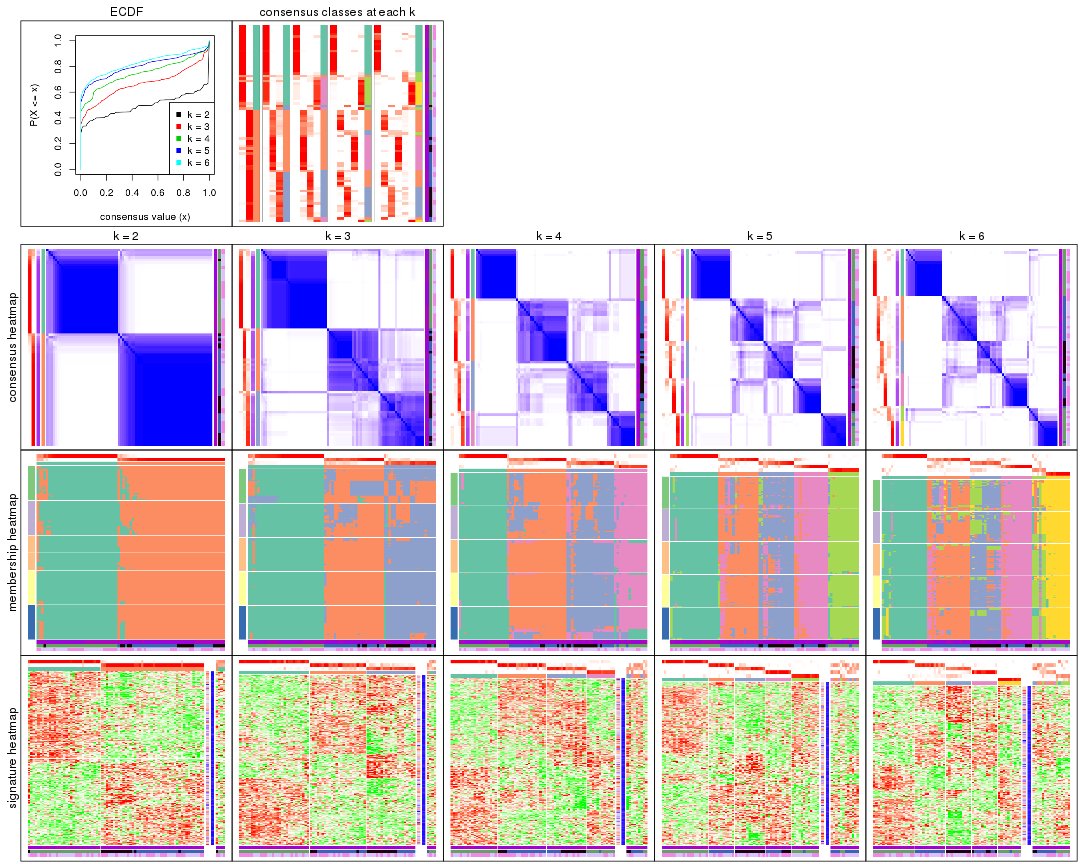
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
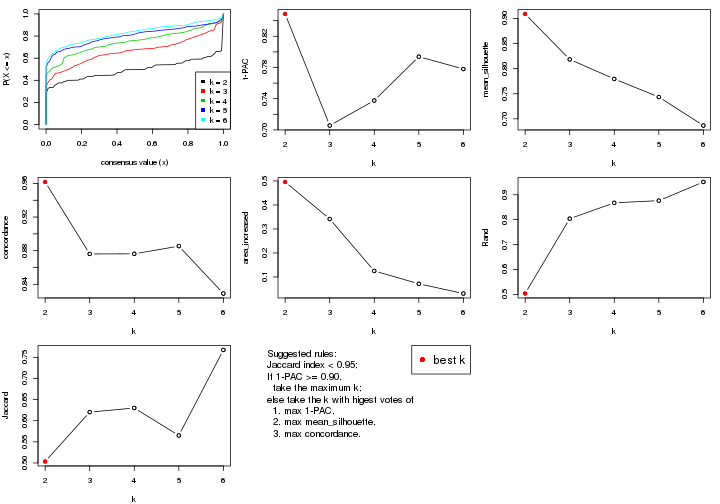
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.849 0.909 0.962 0.4958 0.503 0.503
#> 3 3 0.706 0.818 0.876 0.3416 0.804 0.620
#> 4 4 0.738 0.780 0.876 0.1252 0.868 0.630
#> 5 5 0.794 0.743 0.885 0.0716 0.876 0.565
#> 6 6 0.778 0.687 0.829 0.0311 0.951 0.767
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.967 0.000 1.000
#> GSM907859 2 0.7745 0.704 0.228 0.772
#> GSM907860 2 0.0000 0.967 0.000 1.000
#> GSM907854 2 0.0000 0.967 0.000 1.000
#> GSM907855 2 0.0000 0.967 0.000 1.000
#> GSM907856 2 0.0000 0.967 0.000 1.000
#> GSM907857 1 0.4690 0.862 0.900 0.100
#> GSM907825 2 0.0000 0.967 0.000 1.000
#> GSM907828 2 0.0000 0.967 0.000 1.000
#> GSM907832 2 0.0000 0.967 0.000 1.000
#> GSM907833 2 0.0000 0.967 0.000 1.000
#> GSM907834 2 0.0000 0.967 0.000 1.000
#> GSM907826 2 0.0000 0.967 0.000 1.000
#> GSM907827 2 0.0000 0.967 0.000 1.000
#> GSM907829 2 0.8327 0.621 0.264 0.736
#> GSM907830 2 0.0376 0.964 0.004 0.996
#> GSM907831 2 0.0000 0.967 0.000 1.000
#> GSM907792 1 0.0000 0.948 1.000 0.000
#> GSM907795 1 0.0000 0.948 1.000 0.000
#> GSM907801 1 0.0000 0.948 1.000 0.000
#> GSM907802 1 0.9661 0.395 0.608 0.392
#> GSM907804 1 0.0000 0.948 1.000 0.000
#> GSM907805 1 0.0000 0.948 1.000 0.000
#> GSM907806 1 0.0000 0.948 1.000 0.000
#> GSM907793 1 0.0000 0.948 1.000 0.000
#> GSM907794 1 0.0000 0.948 1.000 0.000
#> GSM907796 1 0.0000 0.948 1.000 0.000
#> GSM907797 1 0.0000 0.948 1.000 0.000
#> GSM907798 1 0.0000 0.948 1.000 0.000
#> GSM907799 1 0.0000 0.948 1.000 0.000
#> GSM907800 1 0.0000 0.948 1.000 0.000
#> GSM907803 1 0.0000 0.948 1.000 0.000
#> GSM907864 2 0.5178 0.862 0.116 0.884
#> GSM907865 2 0.9686 0.359 0.396 0.604
#> GSM907868 2 0.0000 0.967 0.000 1.000
#> GSM907869 2 0.2948 0.925 0.052 0.948
#> GSM907870 2 0.0000 0.967 0.000 1.000
#> GSM907861 2 0.0000 0.967 0.000 1.000
#> GSM907862 2 0.0000 0.967 0.000 1.000
#> GSM907863 2 0.0000 0.967 0.000 1.000
#> GSM907866 2 0.0000 0.967 0.000 1.000
#> GSM907867 2 0.0000 0.967 0.000 1.000
#> GSM907839 2 0.6973 0.772 0.188 0.812
#> GSM907840 2 0.0376 0.964 0.004 0.996
#> GSM907842 2 0.0376 0.964 0.004 0.996
#> GSM907843 2 0.0000 0.967 0.000 1.000
#> GSM907845 2 0.0376 0.964 0.004 0.996
#> GSM907846 2 0.0000 0.967 0.000 1.000
#> GSM907848 2 0.0000 0.967 0.000 1.000
#> GSM907851 2 0.3584 0.913 0.068 0.932
#> GSM907835 2 0.0000 0.967 0.000 1.000
#> GSM907836 2 0.0000 0.967 0.000 1.000
#> GSM907837 2 0.0000 0.967 0.000 1.000
#> GSM907838 2 0.0000 0.967 0.000 1.000
#> GSM907841 2 0.0000 0.967 0.000 1.000
#> GSM907844 2 0.0000 0.967 0.000 1.000
#> GSM907847 2 0.0000 0.967 0.000 1.000
#> GSM907849 2 0.2778 0.930 0.048 0.952
#> GSM907850 2 0.0000 0.967 0.000 1.000
#> GSM907852 2 0.0000 0.967 0.000 1.000
#> GSM907853 2 0.0000 0.967 0.000 1.000
#> GSM907807 1 0.0000 0.948 1.000 0.000
#> GSM907813 1 0.0376 0.946 0.996 0.004
#> GSM907814 1 0.0000 0.948 1.000 0.000
#> GSM907816 1 0.0000 0.948 1.000 0.000
#> GSM907818 1 0.0000 0.948 1.000 0.000
#> GSM907819 1 0.0000 0.948 1.000 0.000
#> GSM907820 1 0.9909 0.220 0.556 0.444
#> GSM907822 1 0.0000 0.948 1.000 0.000
#> GSM907823 1 0.0000 0.948 1.000 0.000
#> GSM907808 1 0.0000 0.948 1.000 0.000
#> GSM907809 1 0.0000 0.948 1.000 0.000
#> GSM907810 1 0.0000 0.948 1.000 0.000
#> GSM907811 1 0.0000 0.948 1.000 0.000
#> GSM907812 1 0.0000 0.948 1.000 0.000
#> GSM907815 1 0.0938 0.940 0.988 0.012
#> GSM907817 1 0.2778 0.911 0.952 0.048
#> GSM907821 1 0.7528 0.725 0.784 0.216
#> GSM907824 1 0.9850 0.301 0.572 0.428
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.1753 0.82975 0.000 0.048 0.952
#> GSM907859 2 0.0661 0.85204 0.008 0.988 0.004
#> GSM907860 3 0.6180 0.53092 0.000 0.416 0.584
#> GSM907854 3 0.1529 0.82933 0.000 0.040 0.960
#> GSM907855 3 0.5254 0.74455 0.000 0.264 0.736
#> GSM907856 3 0.5254 0.74455 0.000 0.264 0.736
#> GSM907857 3 0.3619 0.72485 0.136 0.000 0.864
#> GSM907825 3 0.2959 0.81786 0.000 0.100 0.900
#> GSM907828 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907832 2 0.4399 0.80959 0.000 0.812 0.188
#> GSM907833 2 0.4121 0.81801 0.000 0.832 0.168
#> GSM907834 3 0.3340 0.79976 0.000 0.120 0.880
#> GSM907826 3 0.2711 0.82025 0.000 0.088 0.912
#> GSM907827 2 0.6062 0.34505 0.000 0.616 0.384
#> GSM907829 3 0.1453 0.81310 0.008 0.024 0.968
#> GSM907830 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907831 3 0.1643 0.82984 0.000 0.044 0.956
#> GSM907792 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907802 3 0.6476 -0.00692 0.448 0.004 0.548
#> GSM907804 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907805 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907794 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907796 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907797 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907798 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907799 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907800 1 0.0892 0.93919 0.980 0.000 0.020
#> GSM907803 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907864 2 0.0747 0.84876 0.016 0.984 0.000
#> GSM907865 2 0.2116 0.82773 0.040 0.948 0.012
#> GSM907868 3 0.4702 0.78388 0.000 0.212 0.788
#> GSM907869 3 0.3267 0.79259 0.000 0.116 0.884
#> GSM907870 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907861 3 0.1643 0.82984 0.000 0.044 0.956
#> GSM907862 3 0.4750 0.75668 0.000 0.216 0.784
#> GSM907863 3 0.4399 0.78430 0.000 0.188 0.812
#> GSM907866 3 0.3879 0.80258 0.000 0.152 0.848
#> GSM907867 3 0.5178 0.75125 0.000 0.256 0.744
#> GSM907839 2 0.1289 0.83811 0.032 0.968 0.000
#> GSM907840 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907842 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907843 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907845 3 0.1753 0.81166 0.000 0.048 0.952
#> GSM907846 2 0.3116 0.82760 0.000 0.892 0.108
#> GSM907848 2 0.4796 0.78802 0.000 0.780 0.220
#> GSM907851 2 0.3921 0.84097 0.016 0.872 0.112
#> GSM907835 3 0.2711 0.82025 0.000 0.088 0.912
#> GSM907836 3 0.3619 0.81625 0.000 0.136 0.864
#> GSM907837 2 0.3619 0.82856 0.000 0.864 0.136
#> GSM907838 2 0.3192 0.83437 0.000 0.888 0.112
#> GSM907841 2 0.5016 0.73416 0.000 0.760 0.240
#> GSM907844 2 0.4504 0.79510 0.000 0.804 0.196
#> GSM907847 2 0.4796 0.78802 0.000 0.780 0.220
#> GSM907849 2 0.0000 0.85529 0.000 1.000 0.000
#> GSM907850 2 0.5098 0.74232 0.000 0.752 0.248
#> GSM907852 2 0.5650 0.69233 0.000 0.688 0.312
#> GSM907853 2 0.5098 0.76773 0.000 0.752 0.248
#> GSM907807 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907813 1 0.0592 0.93806 0.988 0.012 0.000
#> GSM907814 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907818 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907819 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907820 1 0.9625 -0.01450 0.440 0.348 0.212
#> GSM907822 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.94447 1.000 0.000 0.000
#> GSM907812 1 0.1643 0.93101 0.956 0.000 0.044
#> GSM907815 1 0.2711 0.89892 0.912 0.000 0.088
#> GSM907817 1 0.2878 0.89301 0.904 0.000 0.096
#> GSM907821 1 0.5650 0.60004 0.688 0.000 0.312
#> GSM907824 1 0.7284 0.48736 0.620 0.044 0.336
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.2334 0.7930 0.000 0.004 0.908 0.088
#> GSM907859 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907860 3 0.4967 0.3760 0.000 0.452 0.548 0.000
#> GSM907854 3 0.2149 0.7918 0.000 0.000 0.912 0.088
#> GSM907855 3 0.4483 0.7721 0.000 0.104 0.808 0.088
#> GSM907856 3 0.4424 0.7732 0.000 0.100 0.812 0.088
#> GSM907857 3 0.4994 0.2680 0.000 0.000 0.520 0.480
#> GSM907825 3 0.1890 0.7795 0.000 0.056 0.936 0.008
#> GSM907828 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907832 2 0.2773 0.8004 0.000 0.880 0.116 0.004
#> GSM907833 2 0.2281 0.8078 0.000 0.904 0.096 0.000
#> GSM907834 3 0.1890 0.7727 0.000 0.056 0.936 0.008
#> GSM907826 3 0.1151 0.7899 0.000 0.024 0.968 0.008
#> GSM907827 3 0.5273 -0.0666 0.000 0.456 0.536 0.008
#> GSM907829 4 0.2149 0.8274 0.000 0.000 0.088 0.912
#> GSM907830 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907831 3 0.0336 0.7929 0.000 0.000 0.992 0.008
#> GSM907792 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907802 4 0.2469 0.8171 0.000 0.000 0.108 0.892
#> GSM907804 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907805 1 0.3311 0.7631 0.828 0.000 0.000 0.172
#> GSM907806 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907794 4 0.3219 0.8361 0.164 0.000 0.000 0.836
#> GSM907796 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907797 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907798 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907799 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907800 1 0.2530 0.8512 0.888 0.000 0.000 0.112
#> GSM907803 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907864 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907865 2 0.0469 0.8154 0.000 0.988 0.012 0.000
#> GSM907868 3 0.5533 0.6957 0.000 0.220 0.708 0.072
#> GSM907869 3 0.4746 0.5139 0.000 0.000 0.632 0.368
#> GSM907870 2 0.0469 0.8220 0.000 0.988 0.012 0.000
#> GSM907861 3 0.0000 0.7943 0.000 0.000 1.000 0.000
#> GSM907862 3 0.3528 0.6950 0.000 0.192 0.808 0.000
#> GSM907863 3 0.3444 0.7038 0.000 0.184 0.816 0.000
#> GSM907866 3 0.4104 0.7766 0.000 0.080 0.832 0.088
#> GSM907867 3 0.4181 0.7723 0.000 0.128 0.820 0.052
#> GSM907839 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907840 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907842 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907843 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907845 4 0.5548 0.3292 0.000 0.024 0.388 0.588
#> GSM907846 2 0.1474 0.8166 0.000 0.948 0.052 0.000
#> GSM907848 2 0.3810 0.7634 0.000 0.804 0.188 0.008
#> GSM907851 2 0.3933 0.7831 0.024 0.836 0.132 0.008
#> GSM907835 3 0.1151 0.7899 0.000 0.024 0.968 0.008
#> GSM907836 3 0.1256 0.7891 0.000 0.028 0.964 0.008
#> GSM907837 2 0.4746 0.6631 0.000 0.688 0.304 0.008
#> GSM907838 2 0.3636 0.7695 0.000 0.820 0.172 0.008
#> GSM907841 2 0.6252 0.4884 0.000 0.624 0.288 0.088
#> GSM907844 2 0.4746 0.5503 0.000 0.632 0.368 0.000
#> GSM907847 2 0.3852 0.7613 0.000 0.800 0.192 0.008
#> GSM907849 2 0.0000 0.8222 0.000 1.000 0.000 0.000
#> GSM907850 2 0.5220 0.4956 0.000 0.568 0.424 0.008
#> GSM907852 2 0.5244 0.4831 0.000 0.556 0.436 0.008
#> GSM907853 2 0.4936 0.6321 0.000 0.652 0.340 0.008
#> GSM907807 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907813 1 0.1022 0.9481 0.968 0.032 0.000 0.000
#> GSM907814 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907816 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907818 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907819 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907820 2 0.9509 -0.0496 0.260 0.352 0.112 0.276
#> GSM907822 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0000 0.9805 1.000 0.000 0.000 0.000
#> GSM907812 4 0.2281 0.8887 0.096 0.000 0.000 0.904
#> GSM907815 4 0.0336 0.8289 0.008 0.000 0.000 0.992
#> GSM907817 4 0.6523 0.4972 0.348 0.000 0.088 0.564
#> GSM907821 4 0.2466 0.8874 0.096 0.000 0.004 0.900
#> GSM907824 4 0.2408 0.8205 0.000 0.000 0.104 0.896
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.1341 0.75487 0.000 0.056 0.944 0.000 0.000
#> GSM907859 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907860 3 0.3508 0.65150 0.000 0.000 0.748 0.252 0.000
#> GSM907854 3 0.1121 0.76439 0.000 0.044 0.956 0.000 0.000
#> GSM907855 3 0.0609 0.76733 0.000 0.020 0.980 0.000 0.000
#> GSM907856 3 0.0162 0.76587 0.000 0.004 0.996 0.000 0.000
#> GSM907857 3 0.3508 0.57118 0.000 0.000 0.748 0.000 0.252
#> GSM907825 2 0.1410 0.72857 0.000 0.940 0.060 0.000 0.000
#> GSM907828 4 0.1043 0.84536 0.000 0.040 0.000 0.960 0.000
#> GSM907832 2 0.4375 0.17374 0.000 0.576 0.004 0.420 0.000
#> GSM907833 2 0.4397 0.09600 0.000 0.564 0.004 0.432 0.000
#> GSM907834 2 0.0000 0.75235 0.000 1.000 0.000 0.000 0.000
#> GSM907826 2 0.2605 0.66629 0.000 0.852 0.148 0.000 0.000
#> GSM907827 2 0.6477 0.29095 0.000 0.496 0.248 0.256 0.000
#> GSM907829 5 0.0703 0.92144 0.000 0.024 0.000 0.000 0.976
#> GSM907830 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907831 2 0.4297 0.00922 0.000 0.528 0.472 0.000 0.000
#> GSM907792 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0865 0.91598 0.000 0.024 0.004 0.000 0.972
#> GSM907804 1 0.0794 0.94627 0.972 0.000 0.000 0.000 0.028
#> GSM907805 1 0.3274 0.69251 0.780 0.000 0.000 0.000 0.220
#> GSM907806 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.1965 0.86949 0.096 0.000 0.000 0.000 0.904
#> GSM907796 5 0.0703 0.93390 0.024 0.000 0.000 0.000 0.976
#> GSM907797 5 0.0794 0.93224 0.028 0.000 0.000 0.000 0.972
#> GSM907798 5 0.0703 0.93390 0.024 0.000 0.000 0.000 0.976
#> GSM907799 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907800 1 0.2561 0.83227 0.856 0.000 0.000 0.000 0.144
#> GSM907803 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907865 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907868 3 0.2179 0.75697 0.000 0.004 0.896 0.100 0.000
#> GSM907869 3 0.3143 0.63647 0.000 0.000 0.796 0.000 0.204
#> GSM907870 4 0.2179 0.79589 0.000 0.112 0.000 0.888 0.000
#> GSM907861 3 0.3707 0.55070 0.000 0.284 0.716 0.000 0.000
#> GSM907862 3 0.4203 0.65785 0.000 0.188 0.760 0.052 0.000
#> GSM907863 3 0.4193 0.63304 0.000 0.212 0.748 0.040 0.000
#> GSM907866 3 0.0162 0.76612 0.000 0.004 0.996 0.000 0.000
#> GSM907867 3 0.2139 0.76797 0.000 0.032 0.916 0.052 0.000
#> GSM907839 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907840 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907842 4 0.0000 0.86166 0.000 0.000 0.000 1.000 0.000
#> GSM907843 4 0.0162 0.86044 0.000 0.004 0.000 0.996 0.000
#> GSM907845 2 0.1851 0.71884 0.000 0.912 0.000 0.000 0.088
#> GSM907846 4 0.4238 0.33735 0.000 0.368 0.004 0.628 0.000
#> GSM907848 2 0.0771 0.75002 0.000 0.976 0.004 0.020 0.000
#> GSM907851 4 0.4251 0.36518 0.004 0.372 0.000 0.624 0.000
#> GSM907835 2 0.0510 0.75160 0.000 0.984 0.016 0.000 0.000
#> GSM907836 2 0.4445 0.45195 0.000 0.676 0.300 0.024 0.000
#> GSM907837 2 0.3942 0.52114 0.000 0.728 0.012 0.260 0.000
#> GSM907838 4 0.4305 -0.06855 0.000 0.488 0.000 0.512 0.000
#> GSM907841 3 0.5071 0.19187 0.000 0.036 0.540 0.424 0.000
#> GSM907844 3 0.6710 0.20909 0.000 0.264 0.420 0.316 0.000
#> GSM907847 2 0.0771 0.75002 0.000 0.976 0.004 0.020 0.000
#> GSM907849 4 0.1792 0.81451 0.000 0.084 0.000 0.916 0.000
#> GSM907850 2 0.0609 0.75077 0.000 0.980 0.020 0.000 0.000
#> GSM907852 2 0.0290 0.75282 0.000 0.992 0.008 0.000 0.000
#> GSM907853 2 0.0000 0.75235 0.000 1.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.3210 0.72964 0.788 0.000 0.000 0.212 0.000
#> GSM907814 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.0162 0.93055 0.004 0.000 0.000 0.000 0.996
#> GSM907819 5 0.0703 0.93390 0.024 0.000 0.000 0.000 0.976
#> GSM907820 2 0.7526 0.29285 0.224 0.488 0.004 0.060 0.224
#> GSM907822 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.96480 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.0609 0.95088 0.980 0.000 0.000 0.000 0.020
#> GSM907812 5 0.0880 0.93018 0.032 0.000 0.000 0.000 0.968
#> GSM907815 5 0.0880 0.91971 0.000 0.000 0.032 0.000 0.968
#> GSM907817 5 0.6232 0.39424 0.300 0.008 0.140 0.000 0.552
#> GSM907821 5 0.0000 0.92861 0.000 0.000 0.000 0.000 1.000
#> GSM907824 5 0.0162 0.92847 0.000 0.004 0.000 0.000 0.996
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.3619 0.6404 0.000 0.004 0.680 0.000 0.316 0.000
#> GSM907859 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907860 3 0.3463 0.5328 0.000 0.004 0.748 0.240 0.008 0.000
#> GSM907854 3 0.4190 0.6524 0.000 0.048 0.692 0.000 0.260 0.000
#> GSM907855 3 0.2623 0.6756 0.000 0.016 0.852 0.000 0.132 0.000
#> GSM907856 3 0.2631 0.6771 0.000 0.000 0.820 0.000 0.180 0.000
#> GSM907857 3 0.5112 0.5654 0.000 0.000 0.592 0.000 0.296 0.112
#> GSM907825 2 0.2979 0.7140 0.000 0.840 0.044 0.000 0.116 0.000
#> GSM907828 4 0.0935 0.8598 0.000 0.032 0.000 0.964 0.004 0.000
#> GSM907832 2 0.4947 0.0130 0.000 0.480 0.000 0.456 0.064 0.000
#> GSM907833 2 0.4947 -0.0541 0.000 0.480 0.000 0.456 0.064 0.000
#> GSM907834 2 0.1075 0.7228 0.000 0.952 0.000 0.000 0.048 0.000
#> GSM907826 2 0.2383 0.7084 0.000 0.880 0.096 0.000 0.024 0.000
#> GSM907827 2 0.5969 0.5262 0.000 0.584 0.148 0.224 0.044 0.000
#> GSM907829 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907830 4 0.1218 0.8481 0.000 0.004 0.012 0.956 0.028 0.000
#> GSM907831 2 0.4750 0.5392 0.000 0.652 0.252 0.000 0.096 0.000
#> GSM907792 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.3862 0.3334 0.000 0.004 0.000 0.000 0.608 0.388
#> GSM907804 1 0.3823 0.2434 0.564 0.000 0.000 0.000 0.436 0.000
#> GSM907805 1 0.2793 0.6975 0.800 0.000 0.000 0.000 0.000 0.200
#> GSM907806 1 0.2527 0.7655 0.832 0.000 0.000 0.000 0.168 0.000
#> GSM907793 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 6 0.1501 0.8639 0.076 0.000 0.000 0.000 0.000 0.924
#> GSM907796 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907797 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907798 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907799 1 0.0363 0.9137 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907800 5 0.5121 0.2957 0.332 0.000 0.000 0.000 0.568 0.100
#> GSM907803 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907865 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907868 3 0.2841 0.6281 0.000 0.012 0.848 0.128 0.012 0.000
#> GSM907869 3 0.4443 0.6201 0.000 0.000 0.648 0.000 0.300 0.052
#> GSM907870 4 0.2911 0.7632 0.000 0.144 0.000 0.832 0.024 0.000
#> GSM907861 3 0.4034 0.3335 0.000 0.328 0.652 0.000 0.020 0.000
#> GSM907862 3 0.3956 0.5239 0.000 0.204 0.748 0.040 0.008 0.000
#> GSM907863 3 0.3866 0.4883 0.000 0.232 0.736 0.024 0.008 0.000
#> GSM907866 3 0.3482 0.6416 0.000 0.000 0.684 0.000 0.316 0.000
#> GSM907867 3 0.2950 0.6473 0.000 0.032 0.868 0.064 0.036 0.000
#> GSM907839 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907840 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907842 4 0.0000 0.8712 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907843 4 0.0146 0.8705 0.000 0.004 0.000 0.996 0.000 0.000
#> GSM907845 2 0.2112 0.6970 0.000 0.896 0.000 0.000 0.016 0.088
#> GSM907846 4 0.4688 0.3560 0.000 0.328 0.004 0.616 0.052 0.000
#> GSM907848 2 0.1643 0.7170 0.000 0.924 0.000 0.008 0.068 0.000
#> GSM907851 4 0.4662 -0.0193 0.004 0.464 0.004 0.504 0.024 0.000
#> GSM907835 2 0.0291 0.7309 0.000 0.992 0.004 0.000 0.004 0.000
#> GSM907836 2 0.4077 0.4919 0.000 0.660 0.320 0.008 0.012 0.000
#> GSM907837 2 0.5450 0.5952 0.000 0.672 0.144 0.120 0.064 0.000
#> GSM907838 2 0.6175 0.4364 0.000 0.512 0.160 0.296 0.032 0.000
#> GSM907841 5 0.6414 -0.3064 0.000 0.012 0.308 0.332 0.348 0.000
#> GSM907844 2 0.6910 0.1667 0.000 0.372 0.300 0.276 0.052 0.000
#> GSM907847 2 0.1779 0.7173 0.000 0.920 0.000 0.016 0.064 0.000
#> GSM907849 4 0.2402 0.7815 0.004 0.140 0.000 0.856 0.000 0.000
#> GSM907850 2 0.1151 0.7314 0.000 0.956 0.012 0.000 0.032 0.000
#> GSM907852 2 0.1779 0.7265 0.000 0.920 0.016 0.000 0.064 0.000
#> GSM907853 2 0.0547 0.7292 0.000 0.980 0.000 0.000 0.020 0.000
#> GSM907807 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.2883 0.6699 0.788 0.000 0.000 0.212 0.000 0.000
#> GSM907814 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907818 6 0.1141 0.9249 0.000 0.000 0.000 0.000 0.052 0.948
#> GSM907819 6 0.0146 0.9698 0.004 0.000 0.000 0.000 0.000 0.996
#> GSM907820 5 0.4872 0.3209 0.048 0.304 0.000 0.004 0.632 0.012
#> GSM907822 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.9213 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.2562 0.7562 0.828 0.000 0.000 0.000 0.172 0.000
#> GSM907812 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907815 6 0.0000 0.9728 0.000 0.000 0.000 0.000 0.000 1.000
#> GSM907817 5 0.6107 0.4752 0.064 0.000 0.140 0.000 0.584 0.212
#> GSM907821 6 0.0790 0.9484 0.000 0.000 0.000 0.000 0.032 0.968
#> GSM907824 5 0.4121 0.3401 0.000 0.016 0.000 0.000 0.604 0.380
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
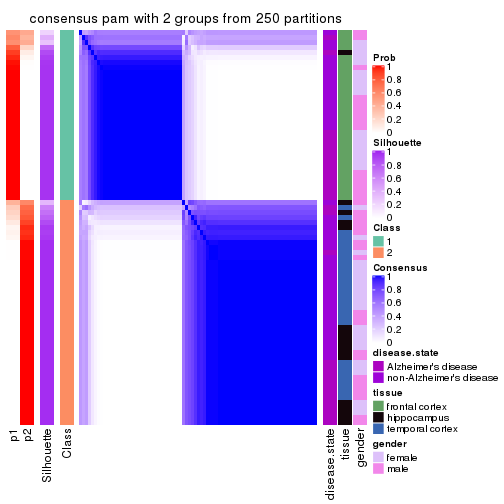
consensus_heatmap(res, k = 3)
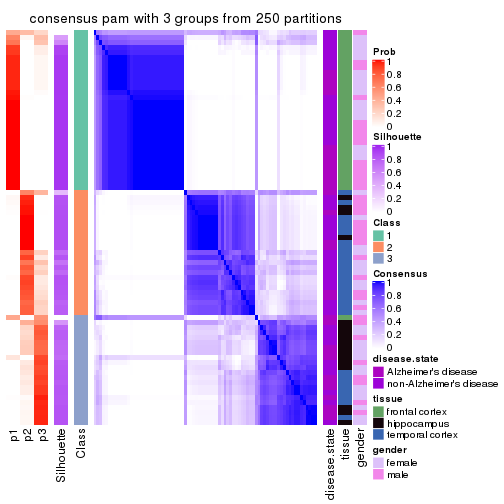
consensus_heatmap(res, k = 4)
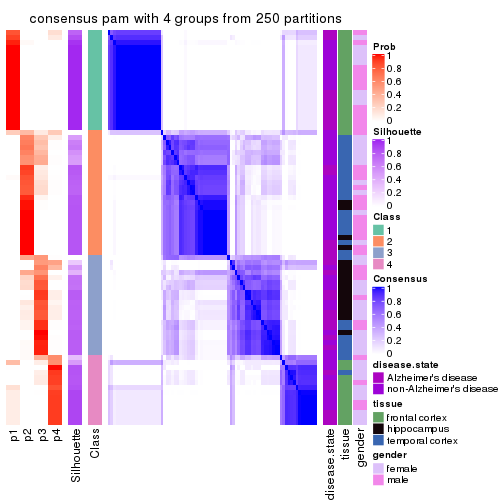
consensus_heatmap(res, k = 5)
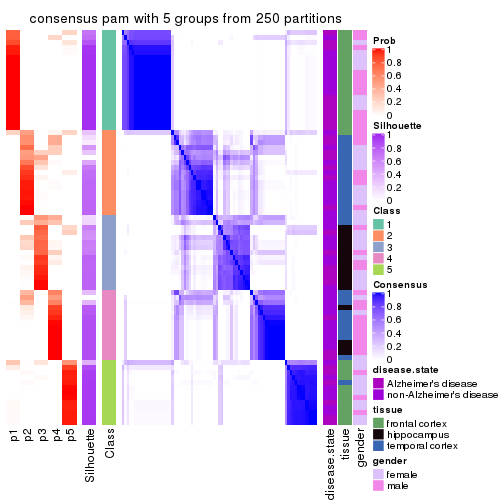
consensus_heatmap(res, k = 6)
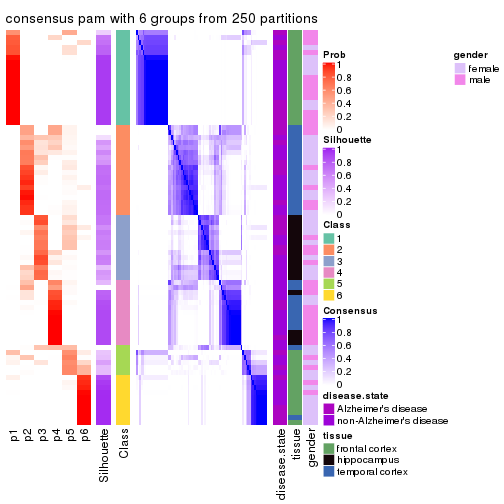
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
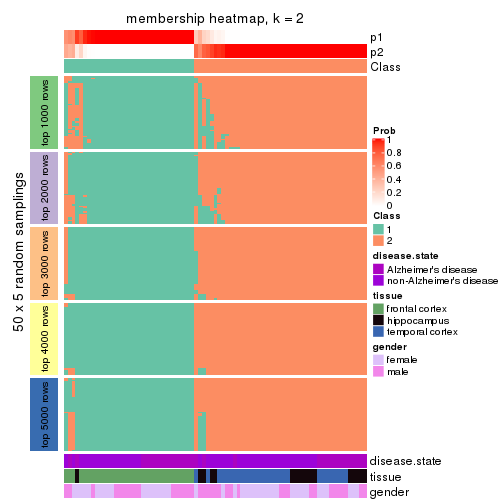
membership_heatmap(res, k = 3)
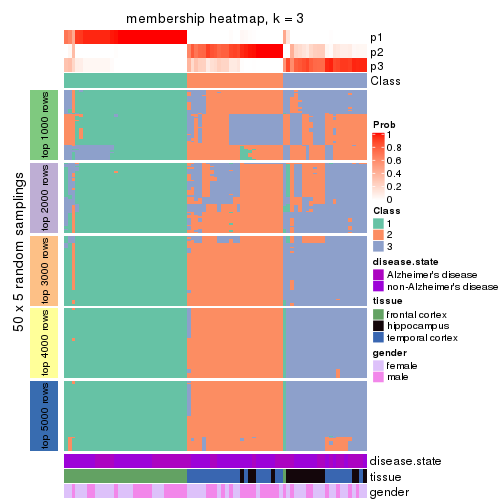
membership_heatmap(res, k = 4)
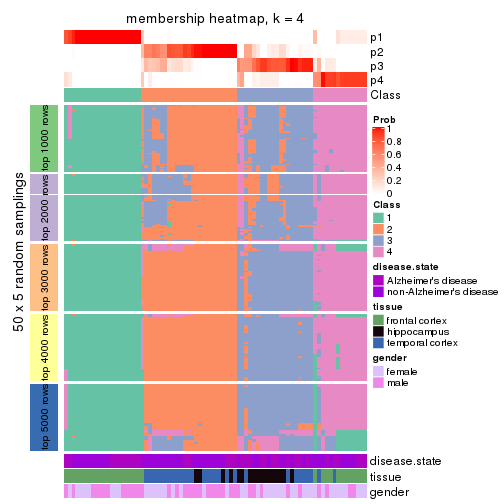
membership_heatmap(res, k = 5)
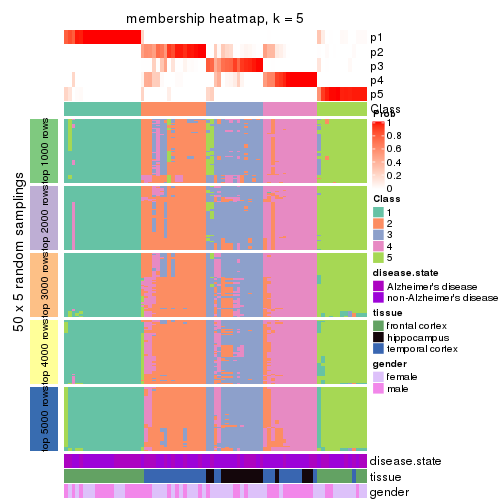
membership_heatmap(res, k = 6)
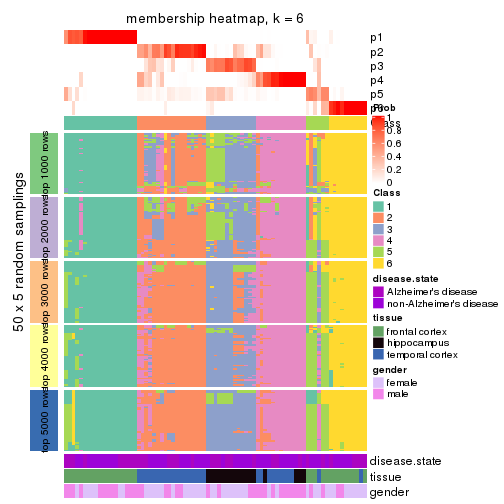
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
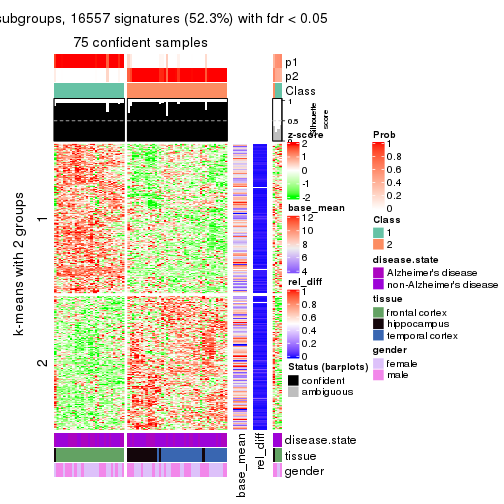
get_signatures(res, k = 3)
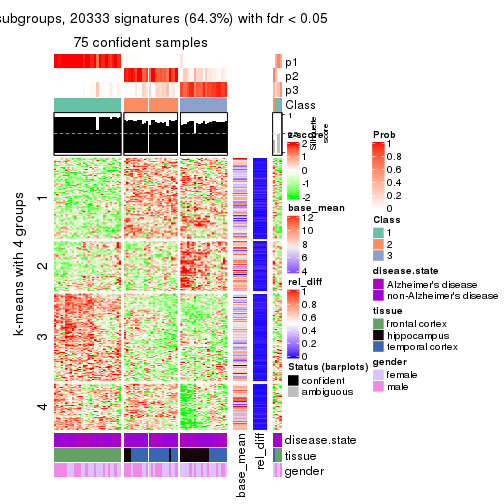
get_signatures(res, k = 4)
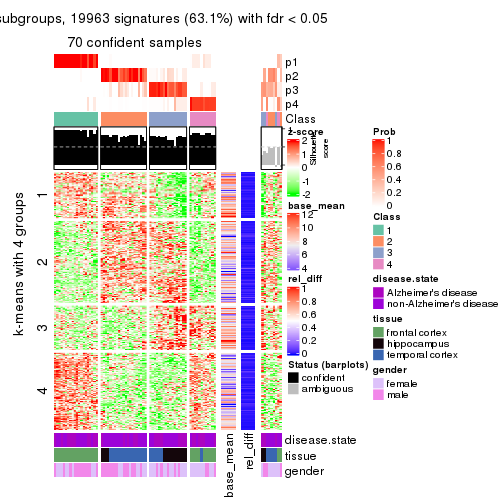
get_signatures(res, k = 5)
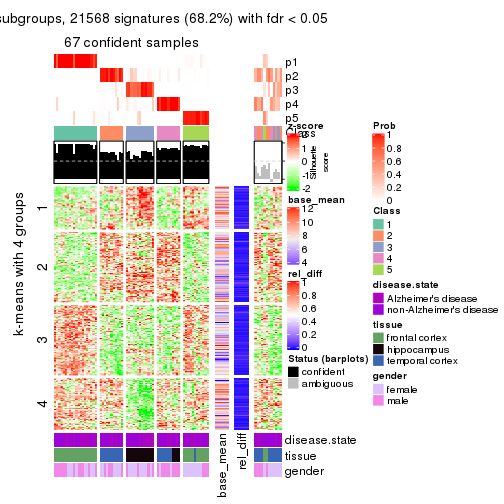
get_signatures(res, k = 6)
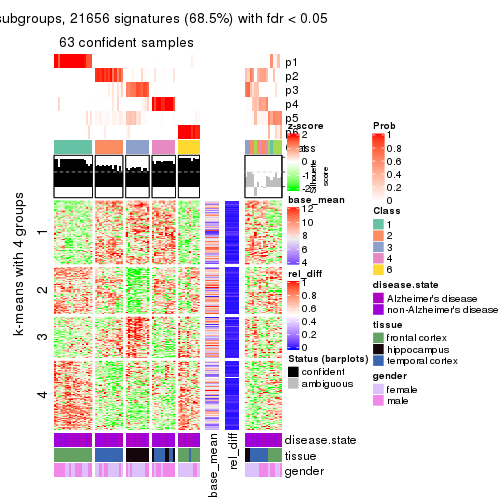
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
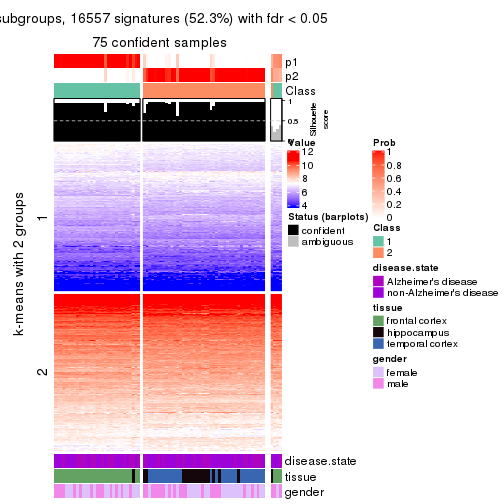
get_signatures(res, k = 3, scale_rows = FALSE)
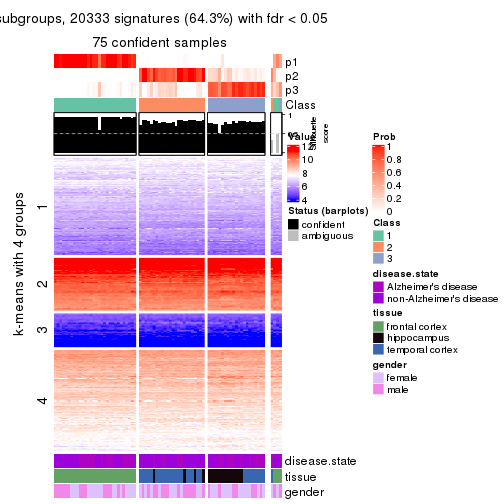
get_signatures(res, k = 4, scale_rows = FALSE)
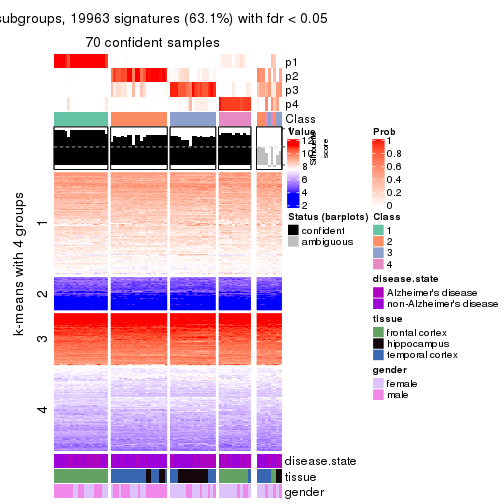
get_signatures(res, k = 5, scale_rows = FALSE)
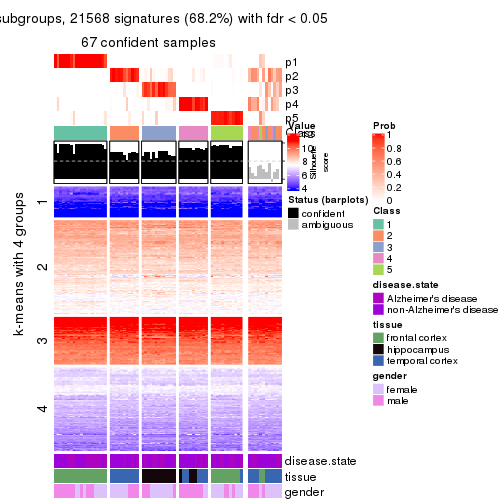
get_signatures(res, k = 6, scale_rows = FALSE)
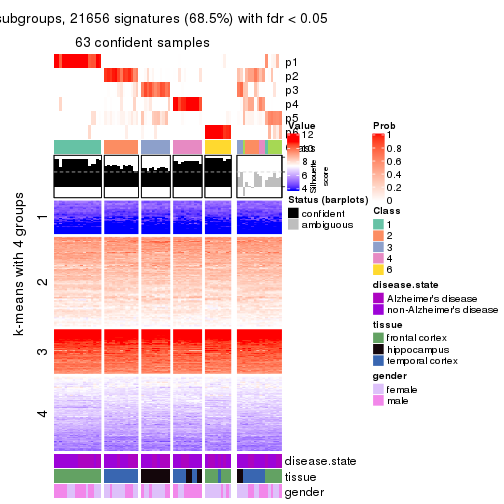
Compare the overlap of signatures from different k:
compare_signatures(res)
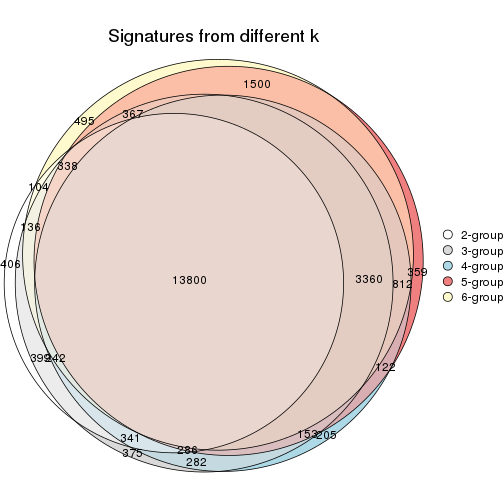
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
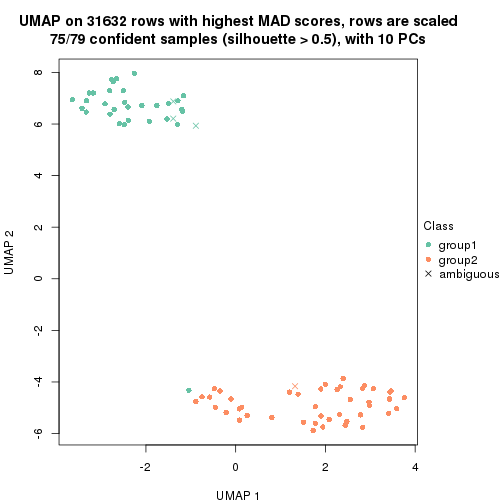
dimension_reduction(res, k = 3, method = "UMAP")
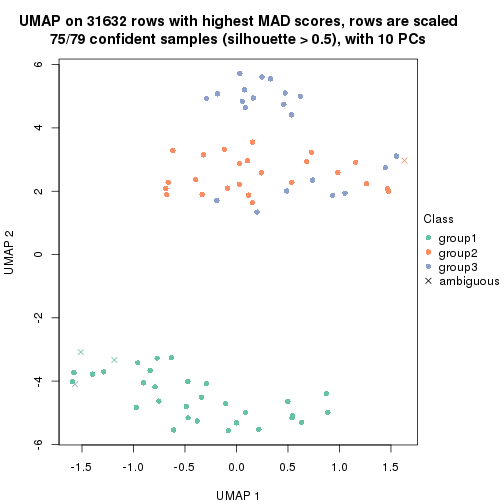
dimension_reduction(res, k = 4, method = "UMAP")
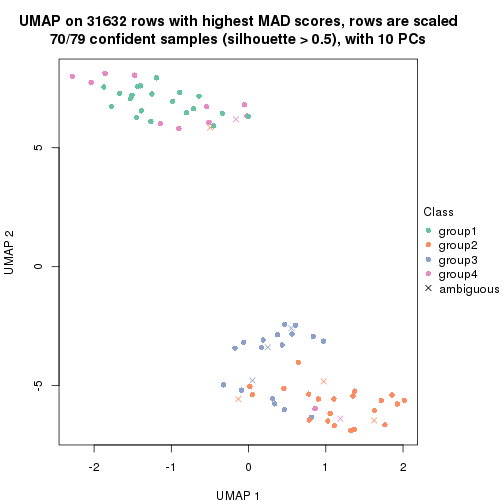
dimension_reduction(res, k = 5, method = "UMAP")
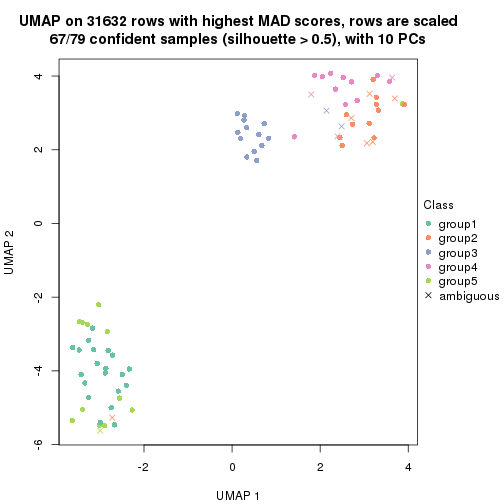
dimension_reduction(res, k = 6, method = "UMAP")
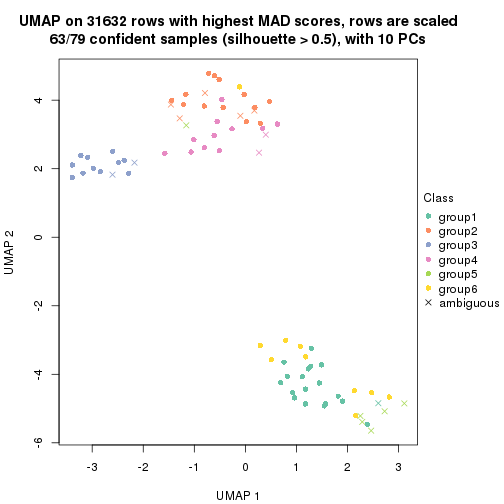
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
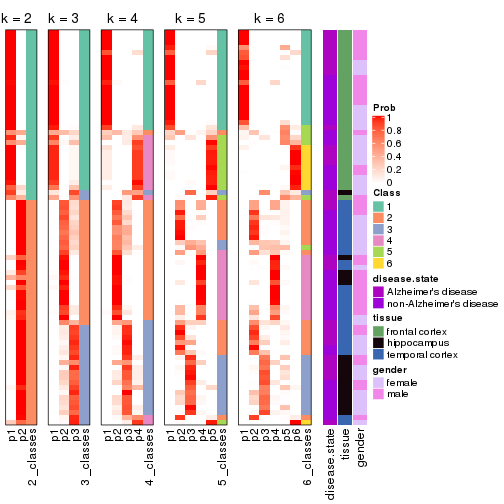
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:pam 75 0.4219 3.58e-16 1.0000 2
#> MAD:pam 75 0.0617 7.14e-19 0.2451 3
#> MAD:pam 70 0.2750 1.96e-15 0.0297 4
#> MAD:pam 67 0.5756 4.23e-20 0.0279 5
#> MAD:pam 63 0.7295 1.10e-18 0.0209 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "mclust"]
# you can also extract it by
# res = res_list["MAD:mclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'mclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
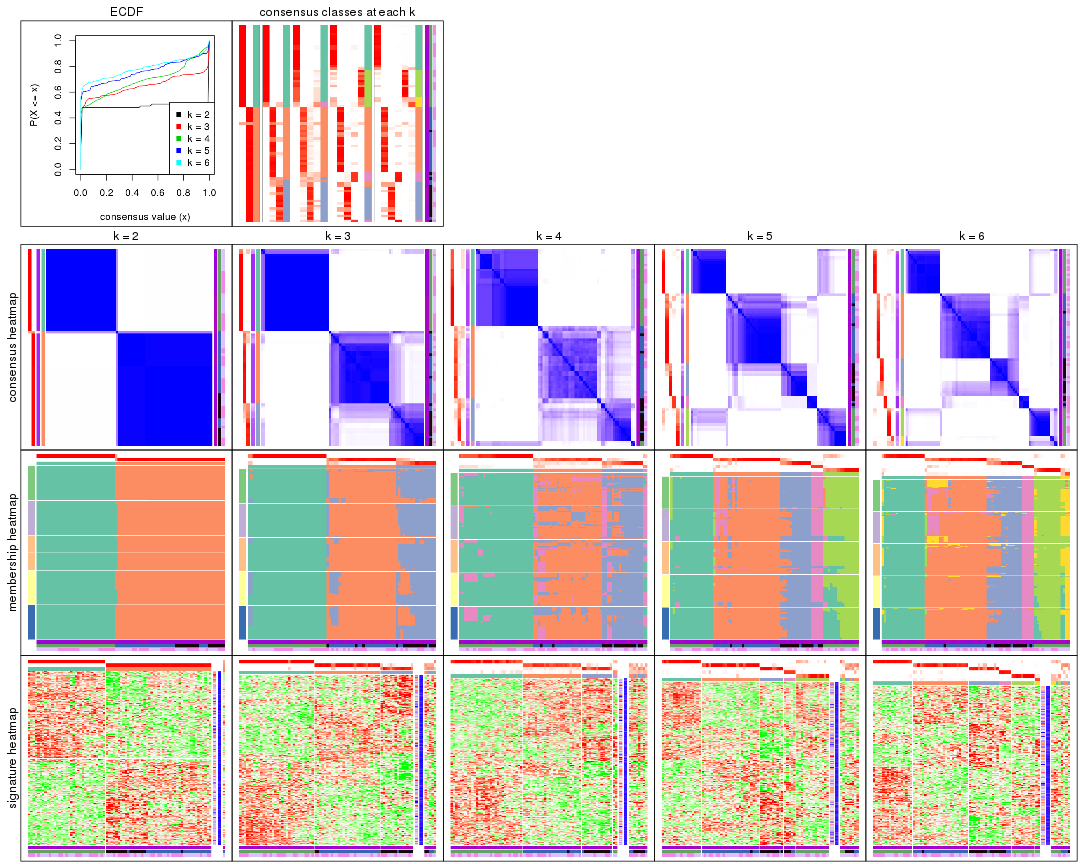
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
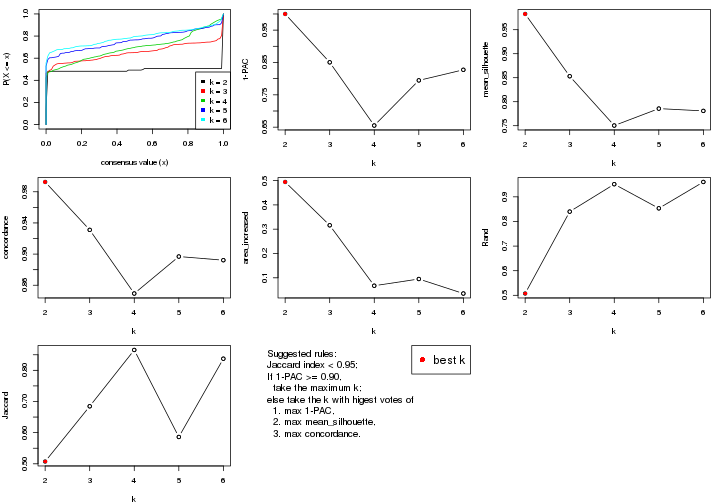
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.983 0.993 0.4943 0.507 0.507
#> 3 3 0.850 0.853 0.931 0.3160 0.840 0.685
#> 4 4 0.655 0.750 0.849 0.0674 0.951 0.865
#> 5 5 0.795 0.786 0.897 0.0950 0.853 0.586
#> 6 6 0.827 0.781 0.892 0.0353 0.960 0.837
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0376 0.989 0.004 0.996
#> GSM907859 2 0.0376 0.989 0.004 0.996
#> GSM907860 2 0.0376 0.989 0.004 0.996
#> GSM907854 2 0.0376 0.989 0.004 0.996
#> GSM907855 2 0.0376 0.989 0.004 0.996
#> GSM907856 2 0.0376 0.989 0.004 0.996
#> GSM907857 2 0.0376 0.989 0.004 0.996
#> GSM907825 2 0.0000 0.987 0.000 1.000
#> GSM907828 2 0.0376 0.989 0.004 0.996
#> GSM907832 2 0.0000 0.987 0.000 1.000
#> GSM907833 2 0.0000 0.987 0.000 1.000
#> GSM907834 2 0.0000 0.987 0.000 1.000
#> GSM907826 2 0.0000 0.987 0.000 1.000
#> GSM907827 2 0.0376 0.989 0.004 0.996
#> GSM907829 2 0.9944 0.169 0.456 0.544
#> GSM907830 2 0.0376 0.989 0.004 0.996
#> GSM907831 2 0.0376 0.989 0.004 0.996
#> GSM907792 1 0.0000 1.000 1.000 0.000
#> GSM907795 1 0.0000 1.000 1.000 0.000
#> GSM907801 1 0.0000 1.000 1.000 0.000
#> GSM907802 1 0.0000 1.000 1.000 0.000
#> GSM907804 1 0.0000 1.000 1.000 0.000
#> GSM907805 1 0.0000 1.000 1.000 0.000
#> GSM907806 1 0.0000 1.000 1.000 0.000
#> GSM907793 1 0.0000 1.000 1.000 0.000
#> GSM907794 1 0.0000 1.000 1.000 0.000
#> GSM907796 1 0.0000 1.000 1.000 0.000
#> GSM907797 1 0.0000 1.000 1.000 0.000
#> GSM907798 1 0.0000 1.000 1.000 0.000
#> GSM907799 1 0.0000 1.000 1.000 0.000
#> GSM907800 1 0.0000 1.000 1.000 0.000
#> GSM907803 1 0.0000 1.000 1.000 0.000
#> GSM907864 2 0.0376 0.989 0.004 0.996
#> GSM907865 2 0.0376 0.989 0.004 0.996
#> GSM907868 2 0.0376 0.989 0.004 0.996
#> GSM907869 2 0.0376 0.989 0.004 0.996
#> GSM907870 2 0.0376 0.989 0.004 0.996
#> GSM907861 2 0.0376 0.989 0.004 0.996
#> GSM907862 2 0.0376 0.989 0.004 0.996
#> GSM907863 2 0.0376 0.989 0.004 0.996
#> GSM907866 2 0.0376 0.989 0.004 0.996
#> GSM907867 2 0.0376 0.989 0.004 0.996
#> GSM907839 2 0.0376 0.989 0.004 0.996
#> GSM907840 2 0.0376 0.989 0.004 0.996
#> GSM907842 2 0.0376 0.989 0.004 0.996
#> GSM907843 2 0.0376 0.989 0.004 0.996
#> GSM907845 2 0.0376 0.989 0.004 0.996
#> GSM907846 2 0.0000 0.987 0.000 1.000
#> GSM907848 2 0.0000 0.987 0.000 1.000
#> GSM907851 2 0.0376 0.989 0.004 0.996
#> GSM907835 2 0.0000 0.987 0.000 1.000
#> GSM907836 2 0.0000 0.987 0.000 1.000
#> GSM907837 2 0.0376 0.989 0.004 0.996
#> GSM907838 2 0.0376 0.989 0.004 0.996
#> GSM907841 2 0.0376 0.989 0.004 0.996
#> GSM907844 2 0.0000 0.987 0.000 1.000
#> GSM907847 2 0.0000 0.987 0.000 1.000
#> GSM907849 2 0.0376 0.989 0.004 0.996
#> GSM907850 2 0.0000 0.987 0.000 1.000
#> GSM907852 2 0.0000 0.987 0.000 1.000
#> GSM907853 2 0.0376 0.989 0.004 0.996
#> GSM907807 1 0.0000 1.000 1.000 0.000
#> GSM907813 1 0.0000 1.000 1.000 0.000
#> GSM907814 1 0.0000 1.000 1.000 0.000
#> GSM907816 1 0.0000 1.000 1.000 0.000
#> GSM907818 1 0.0000 1.000 1.000 0.000
#> GSM907819 1 0.0000 1.000 1.000 0.000
#> GSM907820 1 0.0000 1.000 1.000 0.000
#> GSM907822 1 0.0000 1.000 1.000 0.000
#> GSM907823 1 0.0000 1.000 1.000 0.000
#> GSM907808 1 0.0000 1.000 1.000 0.000
#> GSM907809 1 0.0000 1.000 1.000 0.000
#> GSM907810 1 0.0000 1.000 1.000 0.000
#> GSM907811 1 0.0000 1.000 1.000 0.000
#> GSM907812 1 0.0000 1.000 1.000 0.000
#> GSM907815 1 0.0000 1.000 1.000 0.000
#> GSM907817 1 0.0000 1.000 1.000 0.000
#> GSM907821 1 0.0000 1.000 1.000 0.000
#> GSM907824 1 0.0000 1.000 1.000 0.000
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.1289 0.825 0.000 0.032 0.968
#> GSM907859 2 0.6299 -0.272 0.000 0.524 0.476
#> GSM907860 3 0.1860 0.824 0.000 0.052 0.948
#> GSM907854 3 0.5591 0.664 0.000 0.304 0.696
#> GSM907855 3 0.1289 0.825 0.000 0.032 0.968
#> GSM907856 3 0.1031 0.822 0.000 0.024 0.976
#> GSM907857 3 0.0424 0.805 0.000 0.008 0.992
#> GSM907825 2 0.1289 0.890 0.000 0.968 0.032
#> GSM907828 2 0.0592 0.914 0.000 0.988 0.012
#> GSM907832 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907833 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907834 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907826 2 0.0592 0.914 0.000 0.988 0.012
#> GSM907827 3 0.6244 0.407 0.000 0.440 0.560
#> GSM907829 2 0.6255 0.508 0.012 0.668 0.320
#> GSM907830 2 0.0237 0.914 0.000 0.996 0.004
#> GSM907831 2 0.0892 0.911 0.000 0.980 0.020
#> GSM907792 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907802 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907804 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907805 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907796 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907797 1 0.5650 0.585 0.688 0.000 0.312
#> GSM907798 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907800 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907803 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907864 2 0.0424 0.913 0.000 0.992 0.008
#> GSM907865 3 0.5760 0.646 0.000 0.328 0.672
#> GSM907868 3 0.1643 0.824 0.000 0.044 0.956
#> GSM907869 3 0.0424 0.805 0.000 0.008 0.992
#> GSM907870 2 0.0592 0.914 0.000 0.988 0.012
#> GSM907861 3 0.6154 0.331 0.000 0.408 0.592
#> GSM907862 3 0.3752 0.793 0.000 0.144 0.856
#> GSM907863 3 0.5905 0.608 0.000 0.352 0.648
#> GSM907866 3 0.1289 0.825 0.000 0.032 0.968
#> GSM907867 3 0.3686 0.797 0.000 0.140 0.860
#> GSM907839 2 0.0424 0.913 0.000 0.992 0.008
#> GSM907840 3 0.6225 0.472 0.000 0.432 0.568
#> GSM907842 2 0.0424 0.913 0.000 0.992 0.008
#> GSM907843 2 0.0424 0.913 0.000 0.992 0.008
#> GSM907845 2 0.5706 0.525 0.000 0.680 0.320
#> GSM907846 2 0.5363 0.593 0.000 0.724 0.276
#> GSM907848 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907851 2 0.0000 0.913 0.000 1.000 0.000
#> GSM907835 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907836 2 0.0747 0.913 0.000 0.984 0.016
#> GSM907837 2 0.4842 0.678 0.000 0.776 0.224
#> GSM907838 2 0.2448 0.865 0.000 0.924 0.076
#> GSM907841 3 0.1289 0.825 0.000 0.032 0.968
#> GSM907844 2 0.0747 0.913 0.000 0.984 0.016
#> GSM907847 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907849 2 0.0000 0.913 0.000 1.000 0.000
#> GSM907850 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907852 2 0.0424 0.915 0.000 0.992 0.008
#> GSM907853 2 0.1163 0.894 0.000 0.972 0.028
#> GSM907807 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907813 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907814 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907820 1 0.0237 0.976 0.996 0.000 0.004
#> GSM907822 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907815 1 0.7037 0.499 0.636 0.036 0.328
#> GSM907817 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907821 1 0.0000 0.979 1.000 0.000 0.000
#> GSM907824 1 0.0000 0.979 1.000 0.000 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0592 0.7780 0.000 0.016 0.984 0.000
#> GSM907859 3 0.7664 0.3049 0.000 0.292 0.460 0.248
#> GSM907860 3 0.1854 0.7813 0.000 0.048 0.940 0.012
#> GSM907854 3 0.1209 0.7815 0.000 0.032 0.964 0.004
#> GSM907855 3 0.1059 0.7760 0.000 0.016 0.972 0.012
#> GSM907856 3 0.1059 0.7760 0.000 0.016 0.972 0.012
#> GSM907857 3 0.4746 0.4628 0.000 0.000 0.632 0.368
#> GSM907825 2 0.3793 0.7722 0.000 0.844 0.112 0.044
#> GSM907828 2 0.4149 0.7620 0.000 0.812 0.152 0.036
#> GSM907832 2 0.1902 0.7935 0.000 0.932 0.064 0.004
#> GSM907833 2 0.1978 0.8028 0.000 0.928 0.068 0.004
#> GSM907834 2 0.3402 0.7748 0.000 0.832 0.164 0.004
#> GSM907826 2 0.2773 0.8014 0.000 0.900 0.072 0.028
#> GSM907827 3 0.5113 0.5042 0.000 0.292 0.684 0.024
#> GSM907829 2 0.7586 0.2748 0.008 0.468 0.156 0.368
#> GSM907830 2 0.4163 0.7398 0.000 0.792 0.188 0.020
#> GSM907831 2 0.4610 0.7213 0.000 0.744 0.236 0.020
#> GSM907792 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907802 1 0.3721 0.7532 0.816 0.004 0.004 0.176
#> GSM907804 1 0.1978 0.8658 0.928 0.004 0.000 0.068
#> GSM907805 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907806 1 0.1902 0.8682 0.932 0.004 0.000 0.064
#> GSM907793 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907794 1 0.0817 0.8945 0.976 0.000 0.000 0.024
#> GSM907796 1 0.3311 0.6690 0.828 0.000 0.000 0.172
#> GSM907797 4 0.6101 0.8580 0.388 0.000 0.052 0.560
#> GSM907798 1 0.3764 0.5061 0.784 0.000 0.000 0.216
#> GSM907799 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907800 1 0.3721 0.7532 0.816 0.004 0.004 0.176
#> GSM907803 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907864 2 0.7373 0.3956 0.000 0.508 0.192 0.300
#> GSM907865 3 0.7457 0.4077 0.000 0.220 0.504 0.276
#> GSM907868 3 0.1743 0.7815 0.000 0.056 0.940 0.004
#> GSM907869 3 0.4713 0.4758 0.000 0.000 0.640 0.360
#> GSM907870 2 0.3674 0.7850 0.000 0.848 0.116 0.036
#> GSM907861 3 0.5604 0.6760 0.000 0.160 0.724 0.116
#> GSM907862 3 0.4964 0.6226 0.000 0.256 0.716 0.028
#> GSM907863 3 0.5297 0.5381 0.000 0.292 0.676 0.032
#> GSM907866 3 0.0927 0.7756 0.000 0.016 0.976 0.008
#> GSM907867 3 0.2976 0.7518 0.000 0.120 0.872 0.008
#> GSM907839 2 0.7373 0.3956 0.000 0.508 0.192 0.300
#> GSM907840 2 0.7870 0.0189 0.000 0.392 0.308 0.300
#> GSM907842 2 0.4880 0.7239 0.000 0.760 0.188 0.052
#> GSM907843 2 0.4037 0.7796 0.000 0.824 0.136 0.040
#> GSM907845 2 0.6705 0.5094 0.000 0.608 0.148 0.244
#> GSM907846 2 0.4656 0.7323 0.000 0.784 0.160 0.056
#> GSM907848 2 0.1854 0.7979 0.000 0.940 0.048 0.012
#> GSM907851 2 0.3625 0.7726 0.000 0.828 0.160 0.012
#> GSM907835 2 0.1902 0.8024 0.000 0.932 0.064 0.004
#> GSM907836 2 0.3307 0.7943 0.000 0.868 0.104 0.028
#> GSM907837 2 0.3435 0.8070 0.000 0.864 0.100 0.036
#> GSM907838 2 0.2623 0.8008 0.000 0.908 0.064 0.028
#> GSM907841 3 0.0592 0.7780 0.000 0.016 0.984 0.000
#> GSM907844 2 0.3760 0.7867 0.000 0.836 0.136 0.028
#> GSM907847 2 0.1356 0.8029 0.000 0.960 0.032 0.008
#> GSM907849 2 0.3625 0.7726 0.000 0.828 0.160 0.012
#> GSM907850 2 0.1388 0.8021 0.000 0.960 0.028 0.012
#> GSM907852 2 0.2198 0.8059 0.000 0.920 0.072 0.008
#> GSM907853 2 0.2300 0.7795 0.000 0.920 0.064 0.016
#> GSM907807 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907813 1 0.1211 0.8709 0.960 0.000 0.000 0.040
#> GSM907814 1 0.1389 0.8630 0.952 0.000 0.000 0.048
#> GSM907816 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907818 1 0.1940 0.8638 0.924 0.000 0.000 0.076
#> GSM907819 1 0.1474 0.8815 0.948 0.000 0.000 0.052
#> GSM907820 1 0.3863 0.7470 0.812 0.008 0.004 0.176
#> GSM907822 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0000 0.9047 1.000 0.000 0.000 0.000
#> GSM907812 1 0.0188 0.9033 0.996 0.000 0.000 0.004
#> GSM907815 4 0.7040 0.8739 0.316 0.028 0.076 0.580
#> GSM907817 1 0.3721 0.7532 0.816 0.004 0.004 0.176
#> GSM907821 1 0.3721 0.7532 0.816 0.004 0.004 0.176
#> GSM907824 1 0.3765 0.7477 0.812 0.004 0.004 0.180
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 0.773 0.000 0.000 1.000 0.000 0.000
#> GSM907859 4 0.1732 0.987 0.000 0.000 0.080 0.920 0.000
#> GSM907860 3 0.3398 0.661 0.000 0.216 0.780 0.004 0.000
#> GSM907854 3 0.0162 0.773 0.000 0.004 0.996 0.000 0.000
#> GSM907855 3 0.0000 0.773 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 0.773 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0404 0.769 0.000 0.000 0.988 0.012 0.000
#> GSM907825 2 0.0290 0.885 0.000 0.992 0.000 0.008 0.000
#> GSM907828 2 0.1270 0.864 0.000 0.948 0.000 0.052 0.000
#> GSM907832 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907833 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907834 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907826 2 0.0162 0.888 0.000 0.996 0.004 0.000 0.000
#> GSM907827 2 0.4135 0.370 0.000 0.656 0.340 0.004 0.000
#> GSM907829 2 0.4901 0.528 0.000 0.672 0.000 0.060 0.268
#> GSM907830 2 0.2569 0.828 0.000 0.892 0.040 0.068 0.000
#> GSM907831 2 0.3143 0.666 0.000 0.796 0.204 0.000 0.000
#> GSM907792 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
#> GSM907804 5 0.4015 0.646 0.348 0.000 0.000 0.000 0.652
#> GSM907805 1 0.0510 0.946 0.984 0.000 0.000 0.000 0.016
#> GSM907806 5 0.2127 0.758 0.108 0.000 0.000 0.000 0.892
#> GSM907793 1 0.0162 0.957 0.996 0.000 0.000 0.004 0.000
#> GSM907794 5 0.3210 0.745 0.212 0.000 0.000 0.000 0.788
#> GSM907796 5 0.4161 0.590 0.392 0.000 0.000 0.000 0.608
#> GSM907797 5 0.5376 0.631 0.308 0.000 0.000 0.080 0.612
#> GSM907798 5 0.4249 0.516 0.432 0.000 0.000 0.000 0.568
#> GSM907799 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
#> GSM907803 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907864 4 0.2006 0.989 0.000 0.012 0.072 0.916 0.000
#> GSM907865 4 0.1732 0.987 0.000 0.000 0.080 0.920 0.000
#> GSM907868 3 0.2848 0.701 0.000 0.156 0.840 0.004 0.000
#> GSM907869 3 0.0404 0.769 0.000 0.000 0.988 0.012 0.000
#> GSM907870 2 0.0290 0.887 0.000 0.992 0.000 0.008 0.000
#> GSM907861 3 0.4549 0.249 0.000 0.464 0.528 0.008 0.000
#> GSM907862 3 0.4510 0.355 0.000 0.432 0.560 0.008 0.000
#> GSM907863 2 0.4367 0.269 0.000 0.620 0.372 0.008 0.000
#> GSM907866 3 0.0000 0.773 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.4310 0.448 0.000 0.392 0.604 0.004 0.000
#> GSM907839 4 0.2006 0.989 0.000 0.012 0.072 0.916 0.000
#> GSM907840 4 0.1894 0.990 0.000 0.008 0.072 0.920 0.000
#> GSM907842 2 0.5484 0.298 0.000 0.540 0.068 0.392 0.000
#> GSM907843 2 0.3999 0.533 0.000 0.656 0.000 0.344 0.000
#> GSM907845 2 0.0404 0.885 0.000 0.988 0.000 0.012 0.000
#> GSM907846 2 0.0162 0.888 0.000 0.996 0.000 0.004 0.000
#> GSM907848 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907851 2 0.2929 0.749 0.000 0.820 0.000 0.180 0.000
#> GSM907835 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907837 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907841 3 0.0000 0.773 0.000 0.000 1.000 0.000 0.000
#> GSM907844 2 0.0162 0.888 0.000 0.996 0.004 0.000 0.000
#> GSM907847 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907849 2 0.2773 0.766 0.000 0.836 0.000 0.164 0.000
#> GSM907850 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907852 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.0000 0.889 0.000 1.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.1608 0.895 0.928 0.000 0.000 0.072 0.000
#> GSM907814 1 0.1608 0.895 0.928 0.000 0.000 0.072 0.000
#> GSM907816 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.1608 0.757 0.072 0.000 0.000 0.000 0.928
#> GSM907819 5 0.4138 0.601 0.384 0.000 0.000 0.000 0.616
#> GSM907820 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
#> GSM907822 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.960 1.000 0.000 0.000 0.000 0.000
#> GSM907811 1 0.1341 0.905 0.944 0.000 0.000 0.000 0.056
#> GSM907812 1 0.3857 0.341 0.688 0.000 0.000 0.000 0.312
#> GSM907815 5 0.7534 0.492 0.308 0.136 0.004 0.080 0.472
#> GSM907817 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
#> GSM907821 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
#> GSM907824 5 0.0162 0.747 0.004 0.000 0.000 0.000 0.996
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0291 0.741 0.000 0.000 0.992 0.004 0.000 0.004
#> GSM907859 4 0.0363 0.968 0.000 0.000 0.012 0.988 0.000 0.000
#> GSM907860 3 0.3608 0.660 0.000 0.272 0.716 0.000 0.000 0.012
#> GSM907854 3 0.0363 0.739 0.000 0.000 0.988 0.012 0.000 0.000
#> GSM907855 3 0.0622 0.740 0.000 0.000 0.980 0.008 0.000 0.012
#> GSM907856 3 0.0622 0.740 0.000 0.000 0.980 0.008 0.000 0.012
#> GSM907857 3 0.1007 0.729 0.000 0.000 0.956 0.000 0.000 0.044
#> GSM907825 2 0.0713 0.883 0.000 0.972 0.000 0.000 0.000 0.028
#> GSM907828 2 0.3068 0.821 0.000 0.840 0.000 0.072 0.000 0.088
#> GSM907832 2 0.0363 0.886 0.000 0.988 0.000 0.000 0.000 0.012
#> GSM907833 2 0.0000 0.886 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907834 2 0.0717 0.879 0.000 0.976 0.008 0.000 0.000 0.016
#> GSM907826 2 0.0260 0.885 0.000 0.992 0.000 0.000 0.000 0.008
#> GSM907827 3 0.4185 0.308 0.000 0.492 0.496 0.000 0.000 0.012
#> GSM907829 2 0.5098 0.438 0.000 0.616 0.020 0.012 0.316 0.036
#> GSM907830 2 0.4036 0.754 0.000 0.756 0.000 0.136 0.000 0.108
#> GSM907831 2 0.2170 0.798 0.000 0.888 0.100 0.000 0.000 0.012
#> GSM907792 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907795 1 0.0000 0.945 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0291 0.945 0.992 0.000 0.000 0.004 0.004 0.000
#> GSM907802 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907804 5 0.2454 0.643 0.160 0.000 0.000 0.000 0.840 0.000
#> GSM907805 1 0.0865 0.911 0.964 0.000 0.000 0.000 0.036 0.000
#> GSM907806 5 0.0603 0.874 0.016 0.000 0.000 0.004 0.980 0.000
#> GSM907793 1 0.0000 0.945 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 5 0.1204 0.827 0.056 0.000 0.000 0.000 0.944 0.000
#> GSM907796 6 0.6108 0.453 0.292 0.000 0.000 0.000 0.344 0.364
#> GSM907797 6 0.2362 0.548 0.004 0.000 0.000 0.000 0.136 0.860
#> GSM907798 6 0.6118 0.471 0.328 0.000 0.000 0.000 0.308 0.364
#> GSM907799 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907800 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907803 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907864 4 0.0547 0.982 0.000 0.020 0.000 0.980 0.000 0.000
#> GSM907865 4 0.0146 0.972 0.000 0.000 0.004 0.996 0.000 0.000
#> GSM907868 3 0.1333 0.735 0.000 0.048 0.944 0.000 0.000 0.008
#> GSM907869 3 0.0790 0.734 0.000 0.000 0.968 0.000 0.000 0.032
#> GSM907870 2 0.2333 0.849 0.000 0.884 0.000 0.024 0.000 0.092
#> GSM907861 3 0.3953 0.617 0.000 0.328 0.656 0.000 0.000 0.016
#> GSM907862 3 0.5141 0.510 0.000 0.376 0.556 0.044 0.000 0.024
#> GSM907863 3 0.5163 0.368 0.000 0.444 0.492 0.044 0.000 0.020
#> GSM907866 3 0.0363 0.740 0.000 0.000 0.988 0.000 0.000 0.012
#> GSM907867 3 0.3954 0.588 0.000 0.352 0.636 0.000 0.000 0.012
#> GSM907839 4 0.0547 0.982 0.000 0.020 0.000 0.980 0.000 0.000
#> GSM907840 4 0.0547 0.982 0.000 0.020 0.000 0.980 0.000 0.000
#> GSM907842 2 0.5083 0.486 0.000 0.580 0.000 0.320 0.000 0.100
#> GSM907843 2 0.4895 0.590 0.000 0.632 0.000 0.264 0.000 0.104
#> GSM907845 2 0.0790 0.884 0.000 0.968 0.000 0.000 0.000 0.032
#> GSM907846 2 0.0790 0.885 0.000 0.968 0.000 0.000 0.000 0.032
#> GSM907848 2 0.0547 0.884 0.000 0.980 0.000 0.000 0.000 0.020
#> GSM907851 2 0.4319 0.713 0.000 0.724 0.000 0.168 0.000 0.108
#> GSM907835 2 0.0458 0.885 0.000 0.984 0.000 0.000 0.000 0.016
#> GSM907836 2 0.0000 0.886 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907837 2 0.1643 0.874 0.000 0.924 0.000 0.008 0.000 0.068
#> GSM907838 2 0.1745 0.872 0.000 0.920 0.000 0.012 0.000 0.068
#> GSM907841 3 0.0146 0.741 0.000 0.000 0.996 0.004 0.000 0.000
#> GSM907844 2 0.0725 0.880 0.000 0.976 0.012 0.000 0.000 0.012
#> GSM907847 2 0.0363 0.886 0.000 0.988 0.000 0.000 0.000 0.012
#> GSM907849 2 0.4319 0.713 0.000 0.724 0.000 0.168 0.000 0.108
#> GSM907850 2 0.0000 0.886 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907852 2 0.0547 0.884 0.000 0.980 0.000 0.000 0.000 0.020
#> GSM907853 2 0.0363 0.886 0.000 0.988 0.000 0.000 0.000 0.012
#> GSM907807 1 0.0000 0.945 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.0653 0.938 0.980 0.000 0.000 0.012 0.004 0.004
#> GSM907814 1 0.0405 0.939 0.988 0.000 0.000 0.008 0.000 0.004
#> GSM907816 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907818 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907819 5 0.5569 -0.163 0.256 0.000 0.000 0.000 0.548 0.196
#> GSM907820 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907822 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907823 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907808 1 0.0000 0.945 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0363 0.938 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907810 1 0.0146 0.946 0.996 0.000 0.000 0.000 0.004 0.000
#> GSM907811 1 0.1957 0.809 0.888 0.000 0.000 0.000 0.112 0.000
#> GSM907812 1 0.5624 -0.317 0.488 0.000 0.000 0.000 0.156 0.356
#> GSM907815 6 0.2908 0.516 0.004 0.028 0.012 0.000 0.092 0.864
#> GSM907817 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907821 5 0.0000 0.887 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907824 5 0.0260 0.880 0.000 0.000 0.000 0.000 0.992 0.008
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
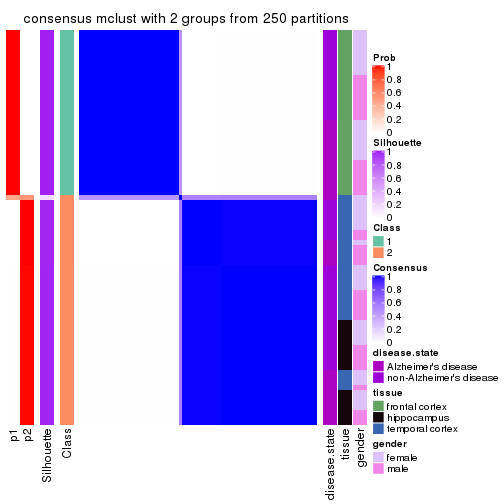
consensus_heatmap(res, k = 3)
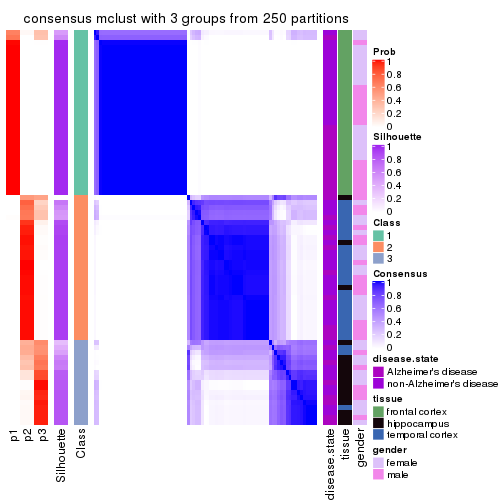
consensus_heatmap(res, k = 4)
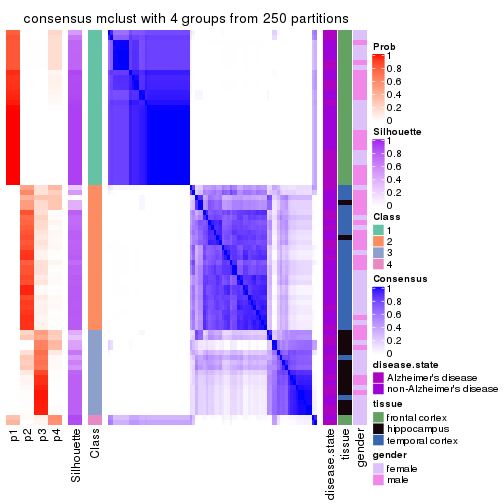
consensus_heatmap(res, k = 5)
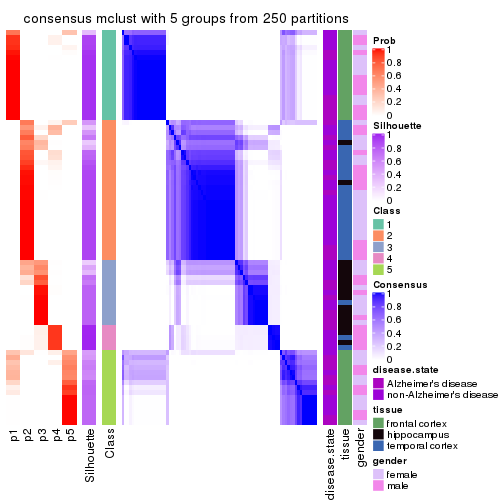
consensus_heatmap(res, k = 6)
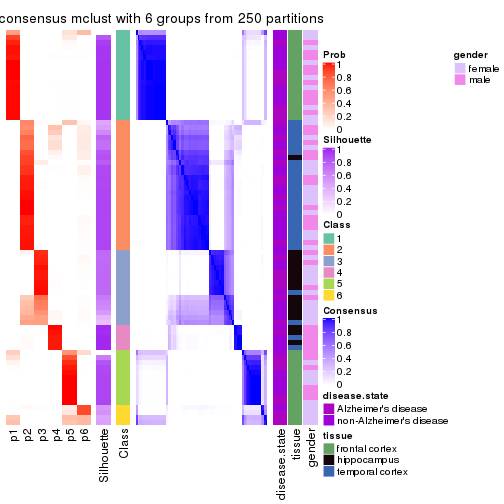
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
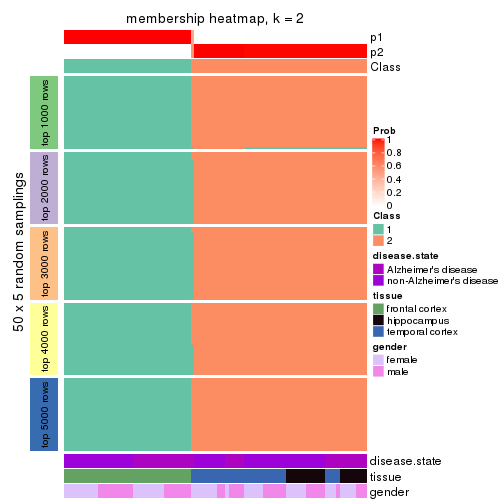
membership_heatmap(res, k = 3)
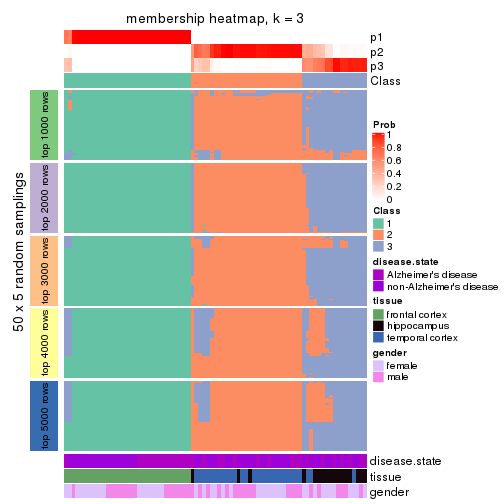
membership_heatmap(res, k = 4)
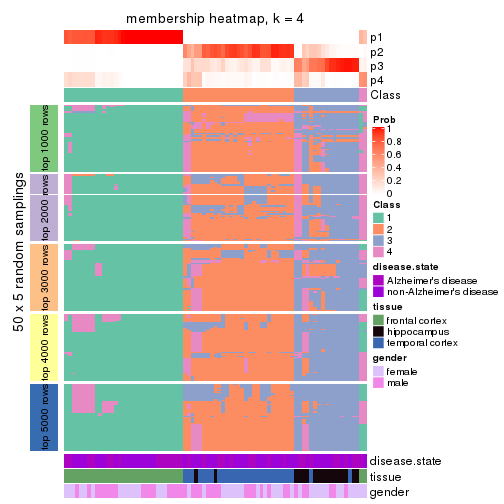
membership_heatmap(res, k = 5)
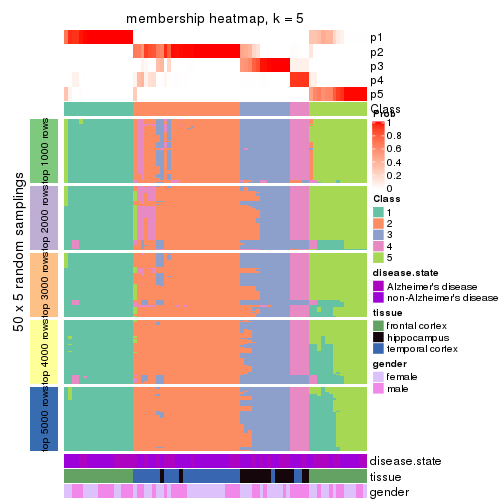
membership_heatmap(res, k = 6)
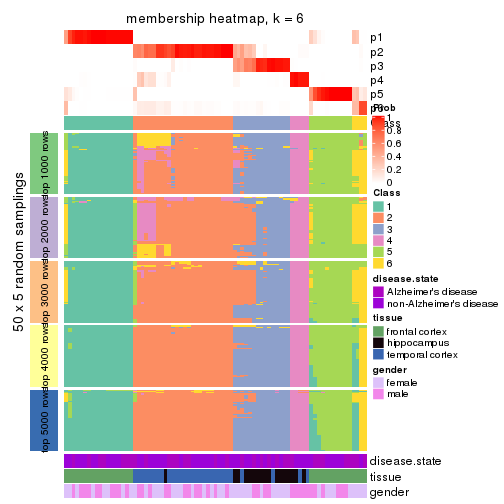
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
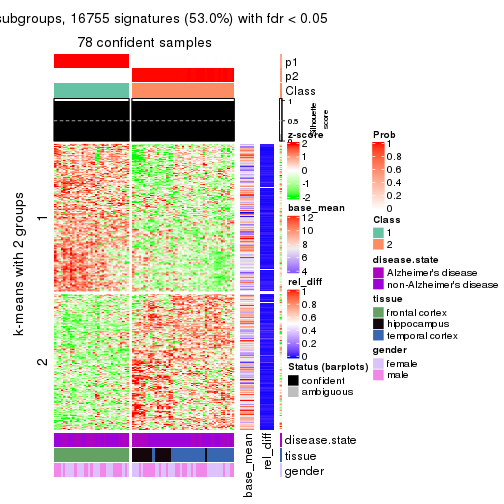
get_signatures(res, k = 3)
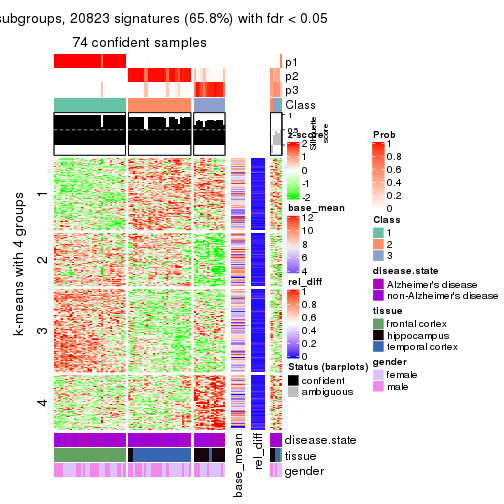
get_signatures(res, k = 4)
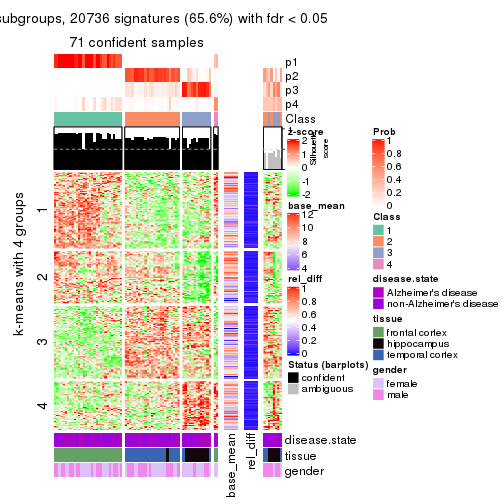
get_signatures(res, k = 5)
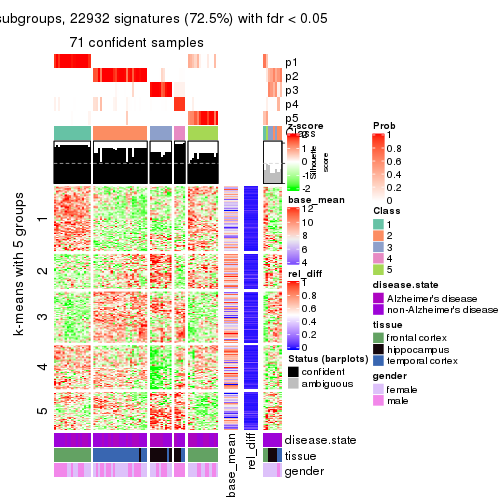
get_signatures(res, k = 6)
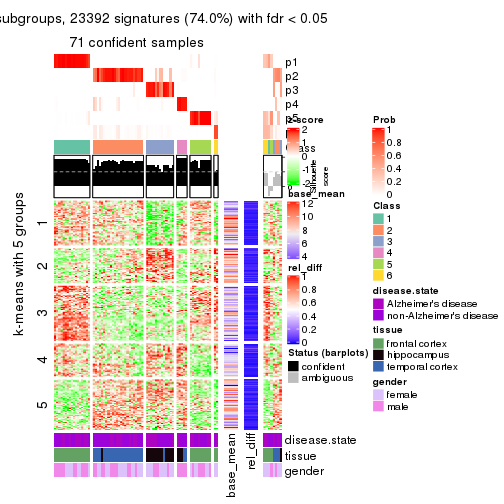
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
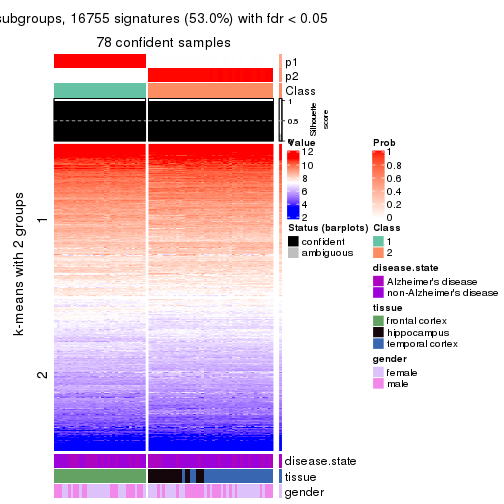
get_signatures(res, k = 3, scale_rows = FALSE)
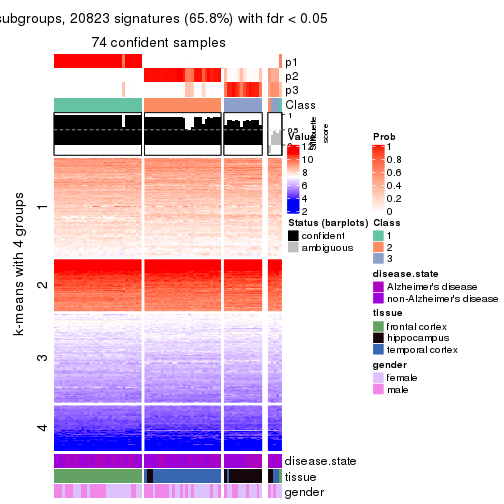
get_signatures(res, k = 4, scale_rows = FALSE)
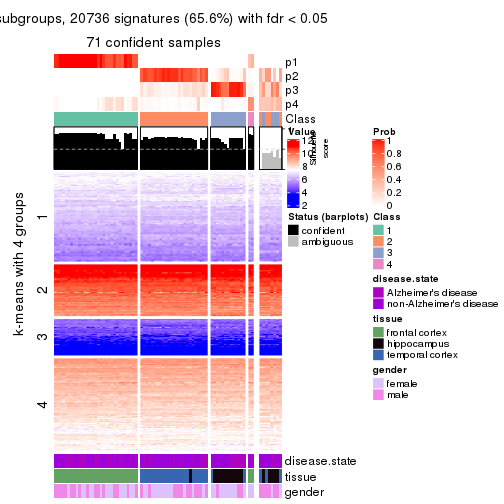
get_signatures(res, k = 5, scale_rows = FALSE)
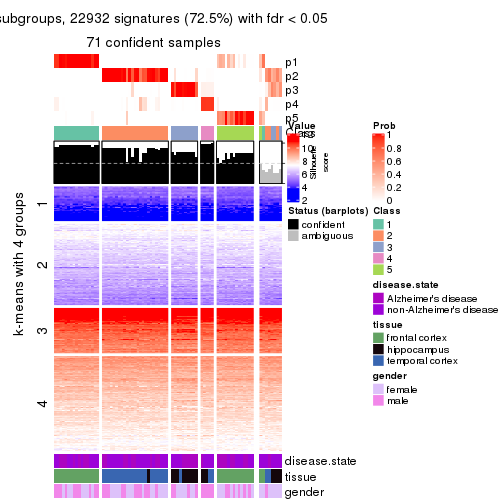
get_signatures(res, k = 6, scale_rows = FALSE)
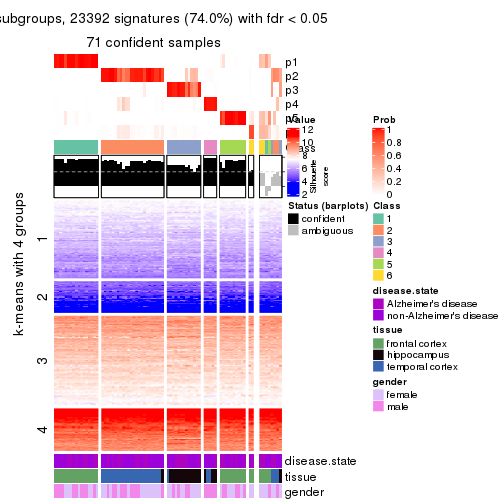
Compare the overlap of signatures from different k:
compare_signatures(res)
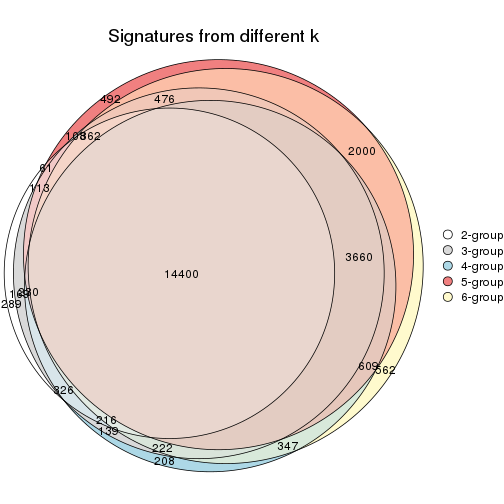
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
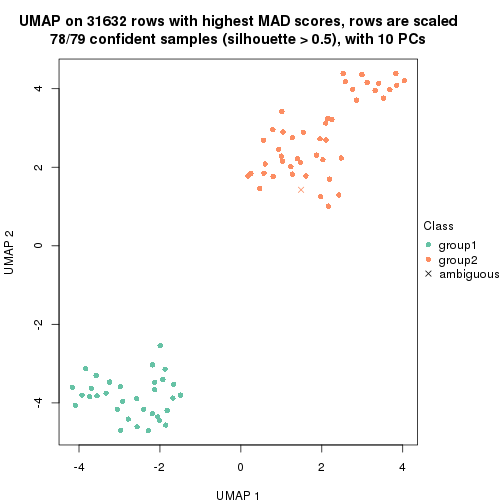
dimension_reduction(res, k = 3, method = "UMAP")
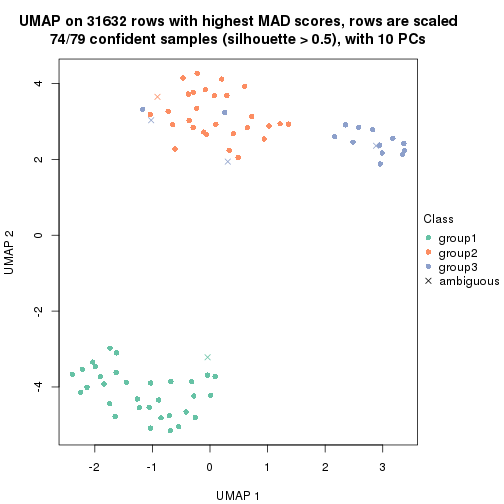
dimension_reduction(res, k = 4, method = "UMAP")
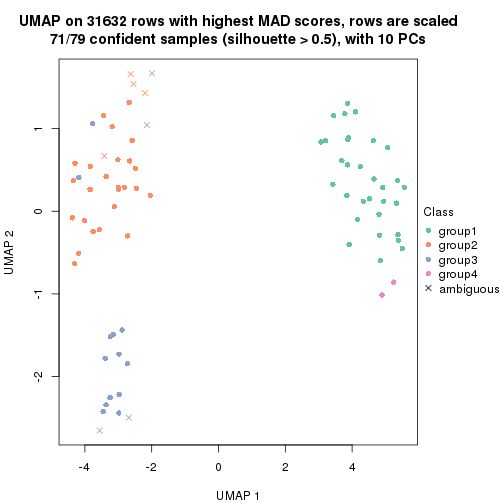
dimension_reduction(res, k = 5, method = "UMAP")
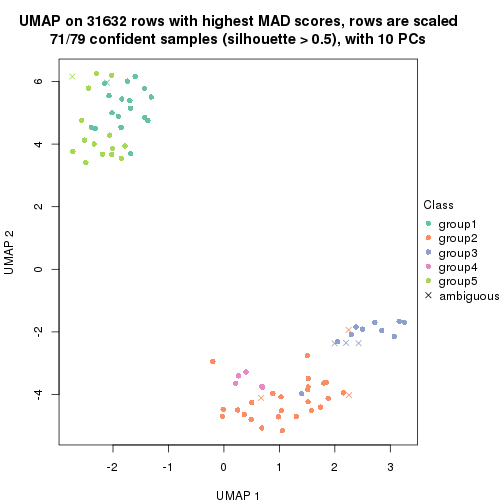
dimension_reduction(res, k = 6, method = "UMAP")
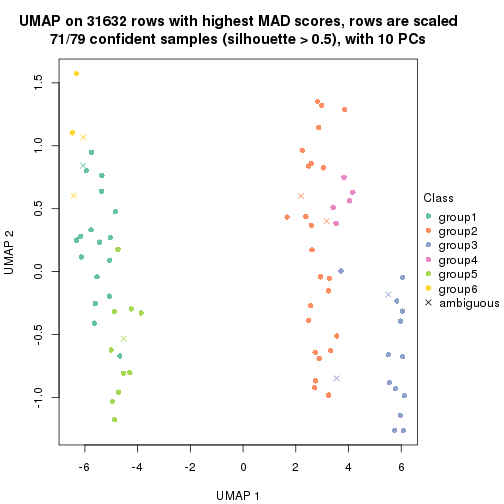
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
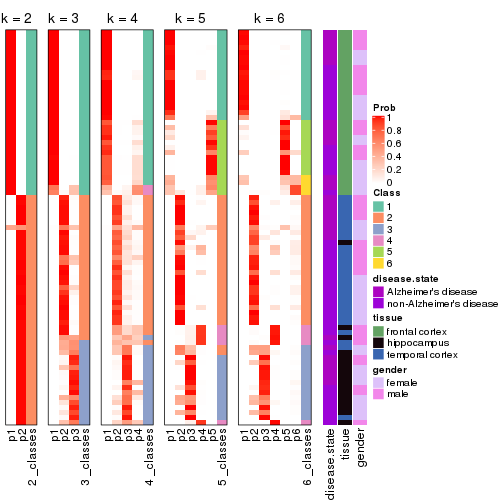
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:mclust 78 0.517 1.15e-17 1.0000 2
#> MAD:mclust 74 0.501 2.05e-26 0.6283 3
#> MAD:mclust 71 0.736 2.56e-23 0.1888 4
#> MAD:mclust 71 0.420 1.23e-21 0.1609 5
#> MAD:mclust 71 0.850 5.27e-21 0.0872 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["MAD", "NMF"]
# you can also extract it by
# res = res_list["MAD:NMF"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'MAD' method.
#> Subgroups are detected by 'NMF' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
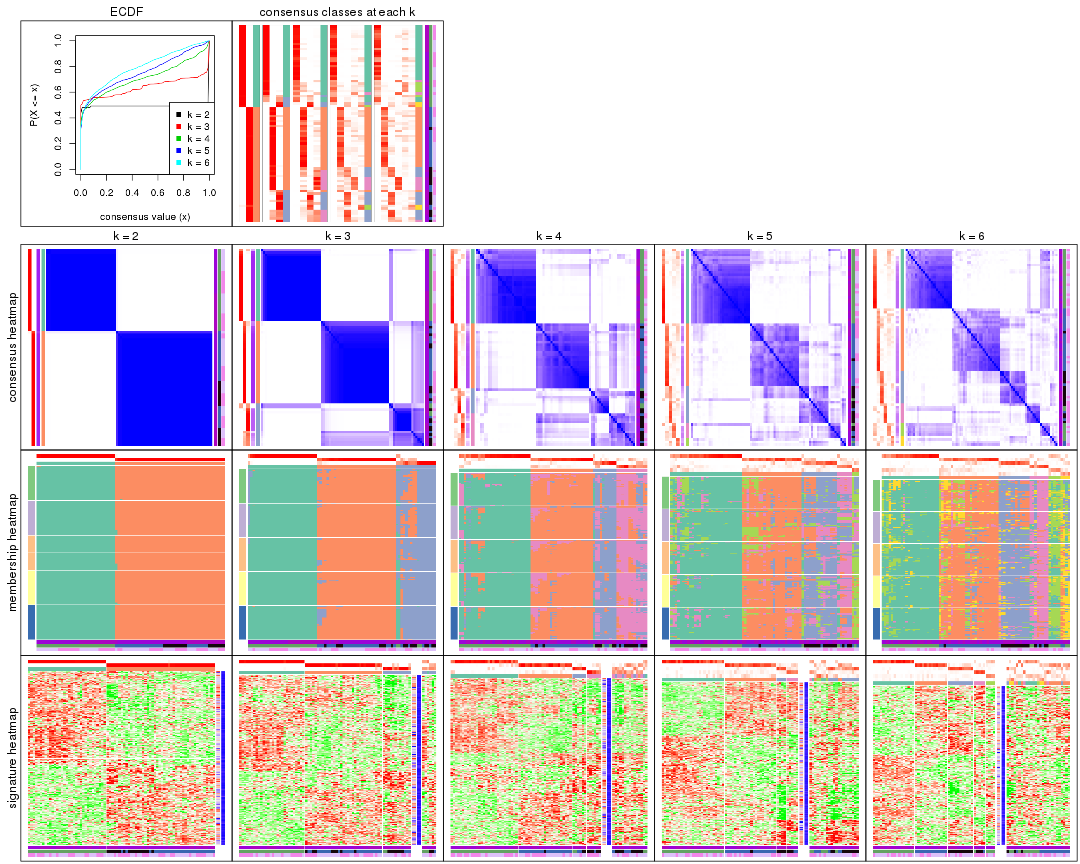
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
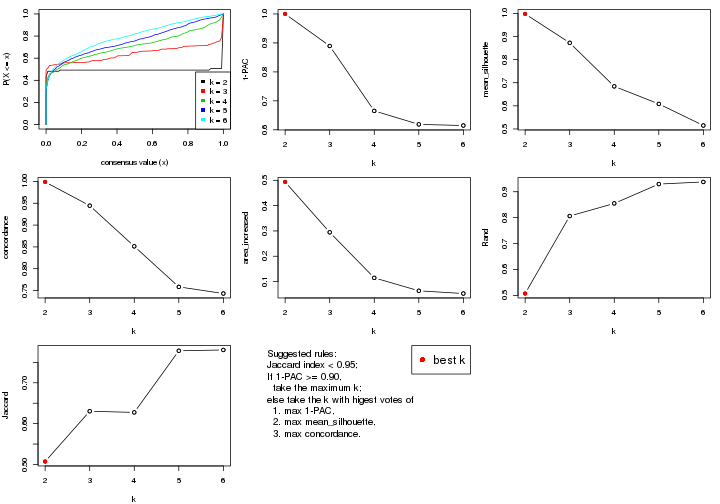
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.998 0.999 0.4935 0.507 0.507
#> 3 3 0.889 0.873 0.945 0.2945 0.806 0.630
#> 4 4 0.665 0.684 0.851 0.1145 0.855 0.627
#> 5 5 0.619 0.608 0.758 0.0634 0.930 0.778
#> 6 6 0.615 0.515 0.743 0.0527 0.938 0.780
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.998 0.000 1.000
#> GSM907859 2 0.0000 0.998 0.000 1.000
#> GSM907860 2 0.0000 0.998 0.000 1.000
#> GSM907854 2 0.0000 0.998 0.000 1.000
#> GSM907855 2 0.0000 0.998 0.000 1.000
#> GSM907856 2 0.0000 0.998 0.000 1.000
#> GSM907857 2 0.0000 0.998 0.000 1.000
#> GSM907825 2 0.0000 0.998 0.000 1.000
#> GSM907828 2 0.0000 0.998 0.000 1.000
#> GSM907832 2 0.0000 0.998 0.000 1.000
#> GSM907833 2 0.0000 0.998 0.000 1.000
#> GSM907834 2 0.0000 0.998 0.000 1.000
#> GSM907826 2 0.0000 0.998 0.000 1.000
#> GSM907827 2 0.0000 0.998 0.000 1.000
#> GSM907829 2 0.3879 0.918 0.076 0.924
#> GSM907830 2 0.0000 0.998 0.000 1.000
#> GSM907831 2 0.0000 0.998 0.000 1.000
#> GSM907792 1 0.0000 1.000 1.000 0.000
#> GSM907795 1 0.0000 1.000 1.000 0.000
#> GSM907801 1 0.0000 1.000 1.000 0.000
#> GSM907802 1 0.0000 1.000 1.000 0.000
#> GSM907804 1 0.0000 1.000 1.000 0.000
#> GSM907805 1 0.0000 1.000 1.000 0.000
#> GSM907806 1 0.0000 1.000 1.000 0.000
#> GSM907793 1 0.0000 1.000 1.000 0.000
#> GSM907794 1 0.0000 1.000 1.000 0.000
#> GSM907796 1 0.0000 1.000 1.000 0.000
#> GSM907797 1 0.0000 1.000 1.000 0.000
#> GSM907798 1 0.0000 1.000 1.000 0.000
#> GSM907799 1 0.0000 1.000 1.000 0.000
#> GSM907800 1 0.0000 1.000 1.000 0.000
#> GSM907803 1 0.0000 1.000 1.000 0.000
#> GSM907864 2 0.0000 0.998 0.000 1.000
#> GSM907865 2 0.0000 0.998 0.000 1.000
#> GSM907868 2 0.0000 0.998 0.000 1.000
#> GSM907869 2 0.0000 0.998 0.000 1.000
#> GSM907870 2 0.0000 0.998 0.000 1.000
#> GSM907861 2 0.0000 0.998 0.000 1.000
#> GSM907862 2 0.0000 0.998 0.000 1.000
#> GSM907863 2 0.0000 0.998 0.000 1.000
#> GSM907866 2 0.0000 0.998 0.000 1.000
#> GSM907867 2 0.0000 0.998 0.000 1.000
#> GSM907839 2 0.0000 0.998 0.000 1.000
#> GSM907840 2 0.0000 0.998 0.000 1.000
#> GSM907842 2 0.0000 0.998 0.000 1.000
#> GSM907843 2 0.0000 0.998 0.000 1.000
#> GSM907845 2 0.0376 0.995 0.004 0.996
#> GSM907846 2 0.0376 0.995 0.004 0.996
#> GSM907848 2 0.0000 0.998 0.000 1.000
#> GSM907851 2 0.0000 0.998 0.000 1.000
#> GSM907835 2 0.0000 0.998 0.000 1.000
#> GSM907836 2 0.0000 0.998 0.000 1.000
#> GSM907837 2 0.0000 0.998 0.000 1.000
#> GSM907838 2 0.0000 0.998 0.000 1.000
#> GSM907841 2 0.0000 0.998 0.000 1.000
#> GSM907844 2 0.0000 0.998 0.000 1.000
#> GSM907847 2 0.0000 0.998 0.000 1.000
#> GSM907849 2 0.0000 0.998 0.000 1.000
#> GSM907850 2 0.0000 0.998 0.000 1.000
#> GSM907852 2 0.0000 0.998 0.000 1.000
#> GSM907853 2 0.0000 0.998 0.000 1.000
#> GSM907807 1 0.0000 1.000 1.000 0.000
#> GSM907813 1 0.0000 1.000 1.000 0.000
#> GSM907814 1 0.0000 1.000 1.000 0.000
#> GSM907816 1 0.0000 1.000 1.000 0.000
#> GSM907818 1 0.0000 1.000 1.000 0.000
#> GSM907819 1 0.0000 1.000 1.000 0.000
#> GSM907820 1 0.0000 1.000 1.000 0.000
#> GSM907822 1 0.0000 1.000 1.000 0.000
#> GSM907823 1 0.0000 1.000 1.000 0.000
#> GSM907808 1 0.0000 1.000 1.000 0.000
#> GSM907809 1 0.0000 1.000 1.000 0.000
#> GSM907810 1 0.0000 1.000 1.000 0.000
#> GSM907811 1 0.0000 1.000 1.000 0.000
#> GSM907812 1 0.0000 1.000 1.000 0.000
#> GSM907815 1 0.0376 0.996 0.996 0.004
#> GSM907817 1 0.0000 1.000 1.000 0.000
#> GSM907821 1 0.0376 0.996 0.996 0.004
#> GSM907824 1 0.0000 1.000 1.000 0.000
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.2711 0.7533 0.000 0.088 0.912
#> GSM907859 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907860 2 0.0747 0.9617 0.000 0.984 0.016
#> GSM907854 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907855 3 0.6111 0.4405 0.000 0.396 0.604
#> GSM907856 3 0.5905 0.5214 0.000 0.352 0.648
#> GSM907857 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907825 3 0.5678 0.5737 0.000 0.316 0.684
#> GSM907828 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907832 2 0.0747 0.9622 0.000 0.984 0.016
#> GSM907833 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907834 2 0.5178 0.6169 0.000 0.744 0.256
#> GSM907826 2 0.0592 0.9653 0.000 0.988 0.012
#> GSM907827 2 0.2261 0.9081 0.000 0.932 0.068
#> GSM907829 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907830 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907831 2 0.4931 0.6632 0.000 0.768 0.232
#> GSM907792 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907802 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907804 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907805 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907794 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907796 3 0.6299 -0.0121 0.476 0.000 0.524
#> GSM907797 3 0.0892 0.7710 0.020 0.000 0.980
#> GSM907798 3 0.6302 -0.0184 0.480 0.000 0.520
#> GSM907799 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907800 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907803 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907864 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907865 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907868 3 0.6079 0.4547 0.000 0.388 0.612
#> GSM907869 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907870 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907861 3 0.5058 0.6523 0.000 0.244 0.756
#> GSM907862 2 0.0237 0.9703 0.000 0.996 0.004
#> GSM907863 2 0.0237 0.9703 0.000 0.996 0.004
#> GSM907866 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907867 2 0.2711 0.8853 0.000 0.912 0.088
#> GSM907839 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907840 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907842 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907843 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907845 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907846 2 0.0424 0.9678 0.000 0.992 0.008
#> GSM907848 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907851 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907835 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907836 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907837 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907838 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907841 3 0.6291 0.1925 0.000 0.468 0.532
#> GSM907844 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907849 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907850 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.9724 0.000 1.000 0.000
#> GSM907853 2 0.1643 0.9335 0.000 0.956 0.044
#> GSM907807 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907813 1 0.0592 0.9707 0.988 0.012 0.000
#> GSM907814 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907818 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907820 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907822 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907811 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907812 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907815 3 0.0000 0.7818 0.000 0.000 1.000
#> GSM907817 1 0.0000 0.9844 1.000 0.000 0.000
#> GSM907821 1 0.5926 0.4375 0.644 0.000 0.356
#> GSM907824 1 0.1529 0.9444 0.960 0.000 0.040
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.4981 -0.1149 0.000 0.000 0.536 0.464
#> GSM907859 4 0.0188 0.5549 0.000 0.004 0.000 0.996
#> GSM907860 4 0.4594 0.5713 0.000 0.280 0.008 0.712
#> GSM907854 3 0.0188 0.6570 0.000 0.000 0.996 0.004
#> GSM907855 4 0.6761 0.5240 0.000 0.168 0.224 0.608
#> GSM907856 4 0.6521 0.4945 0.000 0.124 0.256 0.620
#> GSM907857 3 0.0188 0.6571 0.000 0.000 0.996 0.004
#> GSM907825 2 0.4268 0.6035 0.004 0.760 0.232 0.004
#> GSM907828 2 0.3356 0.7666 0.000 0.824 0.000 0.176
#> GSM907832 2 0.1297 0.8499 0.000 0.964 0.020 0.016
#> GSM907833 2 0.0921 0.8589 0.000 0.972 0.000 0.028
#> GSM907834 2 0.1940 0.8167 0.000 0.924 0.076 0.000
#> GSM907826 2 0.0000 0.8560 0.000 1.000 0.000 0.000
#> GSM907827 2 0.4761 0.7066 0.000 0.768 0.048 0.184
#> GSM907829 3 0.2266 0.6358 0.004 0.084 0.912 0.000
#> GSM907830 2 0.4776 0.3737 0.000 0.624 0.000 0.376
#> GSM907831 2 0.2300 0.8295 0.000 0.920 0.064 0.016
#> GSM907792 1 0.0000 0.8931 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0469 0.8922 0.988 0.000 0.000 0.012
#> GSM907801 1 0.0469 0.8925 0.988 0.000 0.000 0.012
#> GSM907802 1 0.4234 0.7032 0.764 0.228 0.004 0.004
#> GSM907804 1 0.0469 0.8919 0.988 0.000 0.000 0.012
#> GSM907805 1 0.0707 0.8904 0.980 0.000 0.000 0.020
#> GSM907806 1 0.0592 0.8896 0.984 0.016 0.000 0.000
#> GSM907793 1 0.0188 0.8931 0.996 0.000 0.000 0.004
#> GSM907794 1 0.2216 0.8475 0.908 0.092 0.000 0.000
#> GSM907796 1 0.4963 0.5999 0.696 0.020 0.284 0.000
#> GSM907797 3 0.1557 0.6429 0.056 0.000 0.944 0.000
#> GSM907798 1 0.3852 0.7393 0.800 0.008 0.192 0.000
#> GSM907799 1 0.0000 0.8931 1.000 0.000 0.000 0.000
#> GSM907800 1 0.2149 0.8506 0.912 0.088 0.000 0.000
#> GSM907803 1 0.0188 0.8929 0.996 0.004 0.000 0.000
#> GSM907864 4 0.3024 0.5947 0.000 0.148 0.000 0.852
#> GSM907865 4 0.0336 0.5586 0.000 0.008 0.000 0.992
#> GSM907868 4 0.6798 0.3353 0.000 0.100 0.396 0.504
#> GSM907869 4 0.4955 0.1049 0.000 0.000 0.444 0.556
#> GSM907870 2 0.3172 0.7883 0.000 0.840 0.000 0.160
#> GSM907861 3 0.5309 0.3001 0.000 0.256 0.700 0.044
#> GSM907862 4 0.4996 0.0805 0.000 0.484 0.000 0.516
#> GSM907863 2 0.4855 0.3000 0.000 0.600 0.000 0.400
#> GSM907866 3 0.4776 0.1297 0.000 0.000 0.624 0.376
#> GSM907867 4 0.6148 0.3420 0.000 0.408 0.052 0.540
#> GSM907839 4 0.4406 0.4504 0.000 0.300 0.000 0.700
#> GSM907840 4 0.2281 0.6086 0.000 0.096 0.000 0.904
#> GSM907842 2 0.4643 0.4894 0.000 0.656 0.000 0.344
#> GSM907843 2 0.2704 0.8146 0.000 0.876 0.000 0.124
#> GSM907845 3 0.3486 0.5543 0.000 0.188 0.812 0.000
#> GSM907846 2 0.4104 0.7519 0.000 0.808 0.028 0.164
#> GSM907848 2 0.0592 0.8570 0.000 0.984 0.000 0.016
#> GSM907851 2 0.1716 0.8544 0.000 0.936 0.000 0.064
#> GSM907835 2 0.0000 0.8560 0.000 1.000 0.000 0.000
#> GSM907836 2 0.2011 0.8456 0.000 0.920 0.000 0.080
#> GSM907837 2 0.1716 0.8527 0.000 0.936 0.000 0.064
#> GSM907838 2 0.2216 0.8385 0.000 0.908 0.000 0.092
#> GSM907841 4 0.6235 0.2687 0.000 0.056 0.420 0.524
#> GSM907844 2 0.1302 0.8587 0.000 0.956 0.000 0.044
#> GSM907847 2 0.0000 0.8560 0.000 1.000 0.000 0.000
#> GSM907849 2 0.1302 0.8577 0.000 0.956 0.000 0.044
#> GSM907850 2 0.0336 0.8579 0.000 0.992 0.000 0.008
#> GSM907852 2 0.0000 0.8560 0.000 1.000 0.000 0.000
#> GSM907853 2 0.0000 0.8560 0.000 1.000 0.000 0.000
#> GSM907807 1 0.0188 0.8931 0.996 0.000 0.000 0.004
#> GSM907813 1 0.4072 0.6723 0.748 0.000 0.000 0.252
#> GSM907814 1 0.4454 0.5961 0.692 0.000 0.000 0.308
#> GSM907816 1 0.0592 0.8910 0.984 0.000 0.000 0.016
#> GSM907818 1 0.2334 0.8485 0.908 0.088 0.004 0.000
#> GSM907819 1 0.1042 0.8874 0.972 0.000 0.008 0.020
#> GSM907820 1 0.4837 0.5289 0.648 0.348 0.000 0.004
#> GSM907822 1 0.0336 0.8927 0.992 0.000 0.000 0.008
#> GSM907823 1 0.1109 0.8877 0.968 0.004 0.000 0.028
#> GSM907808 1 0.0000 0.8931 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0188 0.8931 0.996 0.000 0.000 0.004
#> GSM907810 1 0.0000 0.8931 1.000 0.000 0.000 0.000
#> GSM907811 1 0.0336 0.8924 0.992 0.008 0.000 0.000
#> GSM907812 1 0.0000 0.8931 1.000 0.000 0.000 0.000
#> GSM907815 3 0.0336 0.6566 0.000 0.000 0.992 0.008
#> GSM907817 1 0.3649 0.7384 0.796 0.204 0.000 0.000
#> GSM907821 3 0.7514 0.0469 0.384 0.184 0.432 0.000
#> GSM907824 1 0.7033 0.2810 0.508 0.364 0.128 0.000
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.3081 0.4838 0.000 0.004 0.868 0.072 0.056
#> GSM907859 4 0.3848 0.5974 0.000 0.040 0.172 0.788 0.000
#> GSM907860 3 0.4860 0.5296 0.000 0.228 0.704 0.064 0.004
#> GSM907854 3 0.3915 0.3730 0.000 0.012 0.792 0.024 0.172
#> GSM907855 3 0.3649 0.5617 0.000 0.088 0.824 0.088 0.000
#> GSM907856 3 0.3359 0.5492 0.000 0.052 0.848 0.096 0.004
#> GSM907857 3 0.3607 0.2691 0.000 0.000 0.752 0.004 0.244
#> GSM907825 2 0.5585 0.5708 0.004 0.624 0.036 0.028 0.308
#> GSM907828 2 0.2171 0.7424 0.000 0.912 0.024 0.064 0.000
#> GSM907832 2 0.4678 0.5886 0.000 0.668 0.004 0.028 0.300
#> GSM907833 2 0.5329 0.6098 0.000 0.672 0.004 0.104 0.220
#> GSM907834 2 0.4009 0.6232 0.000 0.684 0.000 0.004 0.312
#> GSM907826 2 0.2644 0.7428 0.000 0.896 0.060 0.036 0.008
#> GSM907827 2 0.5283 0.1191 0.000 0.572 0.384 0.032 0.012
#> GSM907829 5 0.4782 0.6103 0.000 0.052 0.244 0.004 0.700
#> GSM907830 2 0.5213 0.5621 0.000 0.704 0.204 0.072 0.020
#> GSM907831 2 0.5913 0.4045 0.000 0.640 0.248 0.068 0.044
#> GSM907792 1 0.0162 0.8468 0.996 0.000 0.000 0.004 0.000
#> GSM907795 1 0.0579 0.8459 0.984 0.000 0.000 0.008 0.008
#> GSM907801 1 0.1661 0.8360 0.940 0.000 0.000 0.036 0.024
#> GSM907802 1 0.6161 0.5753 0.596 0.040 0.000 0.076 0.288
#> GSM907804 1 0.2362 0.8345 0.900 0.000 0.000 0.076 0.024
#> GSM907805 1 0.4121 0.7437 0.788 0.000 0.000 0.112 0.100
#> GSM907806 1 0.1074 0.8467 0.968 0.004 0.000 0.016 0.012
#> GSM907793 1 0.0579 0.8481 0.984 0.000 0.000 0.008 0.008
#> GSM907794 1 0.0833 0.8491 0.976 0.004 0.000 0.016 0.004
#> GSM907796 1 0.3865 0.7645 0.808 0.000 0.092 0.000 0.100
#> GSM907797 3 0.6905 -0.3010 0.272 0.000 0.376 0.004 0.348
#> GSM907798 1 0.2928 0.8072 0.872 0.000 0.064 0.000 0.064
#> GSM907799 1 0.0486 0.8481 0.988 0.004 0.000 0.004 0.004
#> GSM907800 1 0.3567 0.8013 0.848 0.008 0.008 0.092 0.044
#> GSM907803 1 0.0865 0.8466 0.972 0.004 0.000 0.024 0.000
#> GSM907864 4 0.5339 0.6273 0.000 0.224 0.116 0.660 0.000
#> GSM907865 4 0.3909 0.5702 0.000 0.024 0.216 0.760 0.000
#> GSM907868 3 0.2130 0.5611 0.000 0.080 0.908 0.012 0.000
#> GSM907869 3 0.4920 0.2194 0.000 0.000 0.644 0.308 0.048
#> GSM907870 2 0.3966 0.7206 0.004 0.820 0.016 0.116 0.044
#> GSM907861 3 0.6407 0.4364 0.000 0.296 0.572 0.044 0.088
#> GSM907862 3 0.6099 0.3343 0.000 0.380 0.516 0.092 0.012
#> GSM907863 3 0.6134 0.3429 0.000 0.376 0.516 0.096 0.012
#> GSM907866 3 0.2661 0.4638 0.000 0.000 0.888 0.056 0.056
#> GSM907867 3 0.5550 0.4920 0.000 0.280 0.636 0.068 0.016
#> GSM907839 4 0.5289 0.5188 0.000 0.312 0.072 0.616 0.000
#> GSM907840 4 0.5490 0.6299 0.000 0.200 0.148 0.652 0.000
#> GSM907842 2 0.4656 0.5268 0.000 0.700 0.040 0.256 0.004
#> GSM907843 2 0.1569 0.7472 0.000 0.944 0.004 0.044 0.008
#> GSM907845 5 0.3904 0.4513 0.000 0.156 0.052 0.000 0.792
#> GSM907846 2 0.7367 0.1504 0.004 0.432 0.028 0.304 0.232
#> GSM907848 2 0.3925 0.6969 0.000 0.784 0.004 0.032 0.180
#> GSM907851 2 0.4749 0.6920 0.004 0.760 0.008 0.116 0.112
#> GSM907835 2 0.1978 0.7554 0.000 0.932 0.012 0.024 0.032
#> GSM907836 2 0.1560 0.7462 0.000 0.948 0.028 0.020 0.004
#> GSM907837 2 0.4628 0.6394 0.000 0.772 0.084 0.124 0.020
#> GSM907838 2 0.4975 0.5997 0.000 0.740 0.108 0.136 0.016
#> GSM907841 3 0.4978 0.3562 0.000 0.016 0.736 0.156 0.092
#> GSM907844 2 0.3071 0.7180 0.000 0.872 0.080 0.036 0.012
#> GSM907847 2 0.3890 0.7044 0.000 0.792 0.004 0.036 0.168
#> GSM907849 2 0.1041 0.7506 0.004 0.964 0.000 0.032 0.000
#> GSM907850 2 0.2131 0.7519 0.000 0.920 0.008 0.016 0.056
#> GSM907852 2 0.3162 0.7447 0.004 0.876 0.016 0.064 0.040
#> GSM907853 2 0.2625 0.7443 0.000 0.876 0.000 0.016 0.108
#> GSM907807 1 0.0162 0.8468 0.996 0.000 0.000 0.004 0.000
#> GSM907813 1 0.4304 0.1106 0.516 0.000 0.000 0.484 0.000
#> GSM907814 4 0.4242 0.0784 0.428 0.000 0.000 0.572 0.000
#> GSM907816 1 0.0510 0.8479 0.984 0.000 0.000 0.016 0.000
#> GSM907818 1 0.4527 0.6784 0.696 0.004 0.000 0.028 0.272
#> GSM907819 1 0.5148 0.6724 0.700 0.004 0.004 0.084 0.208
#> GSM907820 1 0.7602 0.4163 0.516 0.168 0.000 0.148 0.168
#> GSM907822 1 0.0162 0.8472 0.996 0.000 0.000 0.004 0.000
#> GSM907823 1 0.3740 0.7743 0.820 0.008 0.000 0.128 0.044
#> GSM907808 1 0.0324 0.8467 0.992 0.000 0.000 0.004 0.004
#> GSM907809 1 0.0451 0.8471 0.988 0.000 0.000 0.008 0.004
#> GSM907810 1 0.0162 0.8472 0.996 0.004 0.000 0.000 0.000
#> GSM907811 1 0.3163 0.8025 0.860 0.008 0.004 0.108 0.020
#> GSM907812 1 0.0771 0.8475 0.976 0.000 0.000 0.004 0.020
#> GSM907815 5 0.4350 0.4064 0.004 0.000 0.408 0.000 0.588
#> GSM907817 1 0.4662 0.7561 0.784 0.024 0.012 0.128 0.052
#> GSM907821 1 0.7014 0.2418 0.448 0.028 0.040 0.064 0.420
#> GSM907824 1 0.7314 0.5622 0.604 0.060 0.048 0.148 0.140
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.3777 0.64598 0.000 0.012 0.820 0.060 0.020 0.088
#> GSM907859 4 0.1901 0.66438 0.000 0.028 0.040 0.924 0.008 0.000
#> GSM907860 3 0.3865 0.68348 0.000 0.184 0.768 0.028 0.020 0.000
#> GSM907854 3 0.3028 0.68706 0.000 0.040 0.864 0.008 0.012 0.076
#> GSM907855 3 0.3111 0.70602 0.000 0.056 0.864 0.044 0.004 0.032
#> GSM907856 3 0.2495 0.68939 0.000 0.016 0.892 0.060 0.000 0.032
#> GSM907857 3 0.3437 0.48347 0.000 0.000 0.752 0.008 0.004 0.236
#> GSM907825 2 0.5325 0.55265 0.000 0.688 0.032 0.012 0.108 0.160
#> GSM907828 2 0.2255 0.66043 0.000 0.912 0.036 0.028 0.020 0.004
#> GSM907832 2 0.4955 0.52234 0.000 0.712 0.000 0.040 0.116 0.132
#> GSM907833 2 0.5400 0.49377 0.000 0.676 0.000 0.140 0.124 0.060
#> GSM907834 2 0.6040 0.04526 0.000 0.420 0.000 0.000 0.288 0.292
#> GSM907826 2 0.3323 0.62375 0.000 0.824 0.128 0.000 0.036 0.012
#> GSM907827 2 0.6095 -0.10334 0.000 0.460 0.412 0.016 0.024 0.088
#> GSM907829 6 0.5943 0.46846 0.000 0.204 0.132 0.000 0.060 0.604
#> GSM907830 2 0.6892 0.41402 0.000 0.572 0.128 0.100 0.160 0.040
#> GSM907831 2 0.5789 0.40953 0.000 0.608 0.252 0.004 0.064 0.072
#> GSM907792 1 0.0000 0.75112 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.1010 0.74623 0.960 0.000 0.000 0.000 0.036 0.004
#> GSM907801 1 0.3072 0.66370 0.836 0.000 0.000 0.004 0.124 0.036
#> GSM907802 5 0.5634 0.66752 0.360 0.024 0.000 0.004 0.536 0.076
#> GSM907804 1 0.4365 0.33963 0.672 0.000 0.000 0.020 0.288 0.020
#> GSM907805 1 0.4402 0.53119 0.756 0.004 0.000 0.156 0.048 0.036
#> GSM907806 1 0.2416 0.63668 0.844 0.000 0.000 0.000 0.156 0.000
#> GSM907793 1 0.1268 0.74906 0.952 0.000 0.000 0.008 0.036 0.004
#> GSM907794 1 0.0937 0.74519 0.960 0.000 0.000 0.000 0.040 0.000
#> GSM907796 1 0.4039 0.60809 0.796 0.000 0.060 0.000 0.052 0.092
#> GSM907797 6 0.7571 0.14243 0.220 0.000 0.212 0.008 0.156 0.404
#> GSM907798 1 0.3803 0.66223 0.824 0.000 0.032 0.012 0.064 0.068
#> GSM907799 1 0.0713 0.74728 0.972 0.000 0.000 0.000 0.028 0.000
#> GSM907800 1 0.5104 -0.32190 0.532 0.012 0.008 0.004 0.416 0.028
#> GSM907803 1 0.0937 0.74163 0.960 0.000 0.000 0.000 0.040 0.000
#> GSM907864 4 0.2872 0.65210 0.000 0.140 0.024 0.836 0.000 0.000
#> GSM907865 4 0.2043 0.64743 0.000 0.012 0.064 0.912 0.000 0.012
#> GSM907868 3 0.2107 0.71051 0.000 0.052 0.916 0.016 0.008 0.008
#> GSM907869 4 0.6460 -0.03287 0.000 0.000 0.376 0.420 0.040 0.164
#> GSM907870 2 0.5415 0.49789 0.000 0.676 0.036 0.028 0.204 0.056
#> GSM907861 3 0.4738 0.64478 0.000 0.220 0.704 0.012 0.044 0.020
#> GSM907862 3 0.5015 0.61539 0.000 0.240 0.664 0.016 0.076 0.004
#> GSM907863 3 0.5015 0.61513 0.000 0.240 0.664 0.016 0.076 0.004
#> GSM907866 3 0.3164 0.58697 0.000 0.000 0.832 0.044 0.004 0.120
#> GSM907867 3 0.4265 0.67734 0.000 0.168 0.756 0.012 0.056 0.008
#> GSM907839 4 0.3615 0.48236 0.000 0.292 0.008 0.700 0.000 0.000
#> GSM907840 4 0.2706 0.66325 0.000 0.124 0.024 0.852 0.000 0.000
#> GSM907842 2 0.4088 0.21642 0.000 0.556 0.004 0.436 0.004 0.000
#> GSM907843 2 0.1245 0.66230 0.000 0.952 0.000 0.032 0.016 0.000
#> GSM907845 6 0.5873 0.03852 0.000 0.376 0.000 0.004 0.172 0.448
#> GSM907846 2 0.7846 -0.11088 0.004 0.296 0.004 0.284 0.244 0.168
#> GSM907848 2 0.4403 0.55907 0.000 0.744 0.000 0.040 0.172 0.044
#> GSM907851 2 0.5479 0.48850 0.008 0.672 0.012 0.024 0.196 0.088
#> GSM907835 2 0.0964 0.66499 0.000 0.968 0.016 0.000 0.012 0.004
#> GSM907836 2 0.1972 0.65878 0.000 0.916 0.056 0.000 0.024 0.004
#> GSM907837 2 0.5337 0.46806 0.000 0.628 0.188 0.004 0.176 0.004
#> GSM907838 2 0.6119 0.22695 0.000 0.476 0.252 0.004 0.264 0.004
#> GSM907841 3 0.6806 -0.00153 0.000 0.048 0.460 0.196 0.008 0.288
#> GSM907844 2 0.3642 0.63509 0.000 0.824 0.092 0.008 0.060 0.016
#> GSM907847 2 0.2803 0.63235 0.000 0.872 0.000 0.012 0.064 0.052
#> GSM907849 2 0.1381 0.66572 0.000 0.952 0.020 0.004 0.020 0.004
#> GSM907850 2 0.1495 0.66465 0.000 0.948 0.020 0.004 0.020 0.008
#> GSM907852 2 0.2735 0.66031 0.000 0.880 0.036 0.004 0.068 0.012
#> GSM907853 2 0.3013 0.61505 0.000 0.832 0.000 0.004 0.140 0.024
#> GSM907807 1 0.0260 0.75149 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907813 4 0.3615 0.39051 0.292 0.000 0.000 0.700 0.008 0.000
#> GSM907814 4 0.2994 0.55702 0.208 0.000 0.000 0.788 0.000 0.004
#> GSM907816 1 0.1003 0.74819 0.964 0.000 0.000 0.016 0.020 0.000
#> GSM907818 1 0.5493 -0.29910 0.520 0.004 0.000 0.000 0.356 0.120
#> GSM907819 1 0.6943 -0.03181 0.488 0.004 0.024 0.032 0.228 0.224
#> GSM907820 5 0.5568 0.64006 0.240 0.088 0.004 0.012 0.636 0.020
#> GSM907822 1 0.0260 0.75057 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907823 1 0.4813 0.44491 0.684 0.004 0.000 0.020 0.236 0.056
#> GSM907808 1 0.0777 0.74900 0.972 0.000 0.000 0.000 0.024 0.004
#> GSM907809 1 0.2344 0.71249 0.892 0.000 0.000 0.004 0.076 0.028
#> GSM907810 1 0.0363 0.74953 0.988 0.000 0.000 0.000 0.012 0.000
#> GSM907811 1 0.3703 0.22997 0.688 0.004 0.004 0.000 0.304 0.000
#> GSM907812 1 0.2308 0.70951 0.892 0.000 0.000 0.000 0.068 0.040
#> GSM907815 6 0.4452 0.30052 0.000 0.000 0.292 0.028 0.016 0.664
#> GSM907817 5 0.4736 0.54246 0.432 0.024 0.008 0.000 0.532 0.004
#> GSM907821 5 0.7295 0.46795 0.320 0.012 0.024 0.020 0.352 0.272
#> GSM907824 5 0.5246 0.69858 0.292 0.032 0.044 0.000 0.624 0.008
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
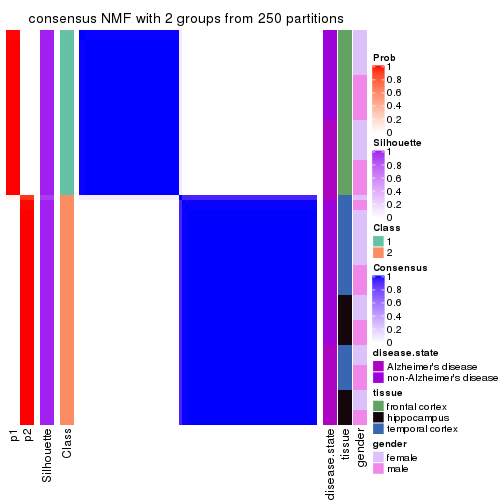
consensus_heatmap(res, k = 3)
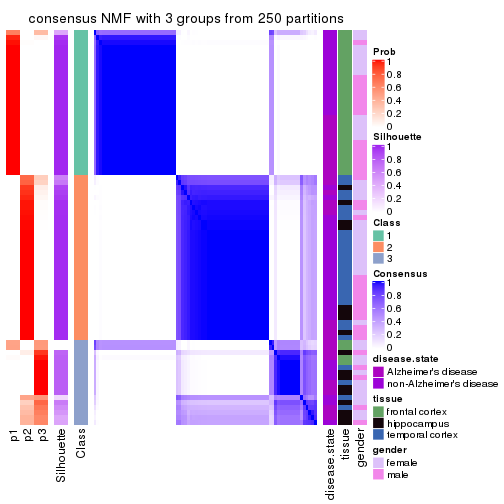
consensus_heatmap(res, k = 4)
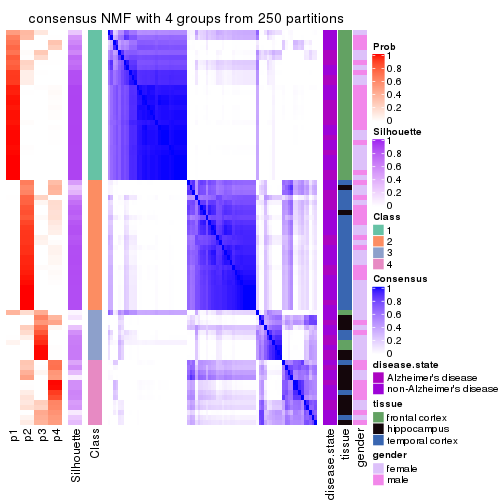
consensus_heatmap(res, k = 5)
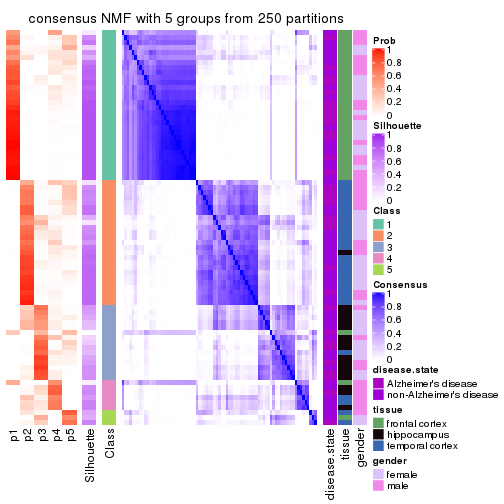
consensus_heatmap(res, k = 6)
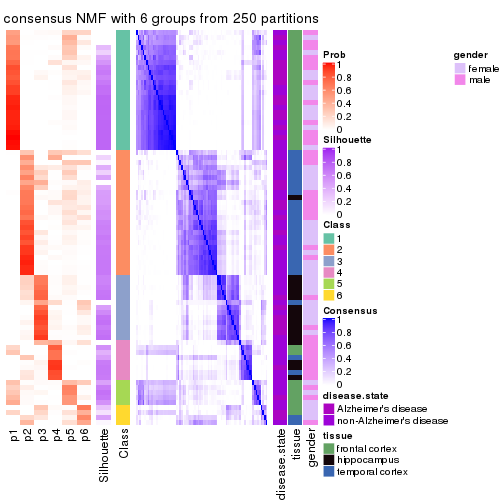
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
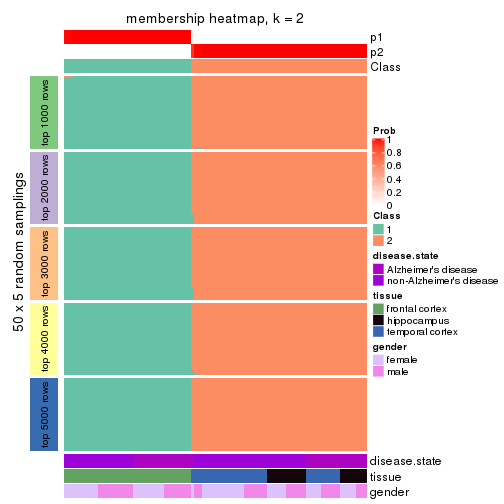
membership_heatmap(res, k = 3)
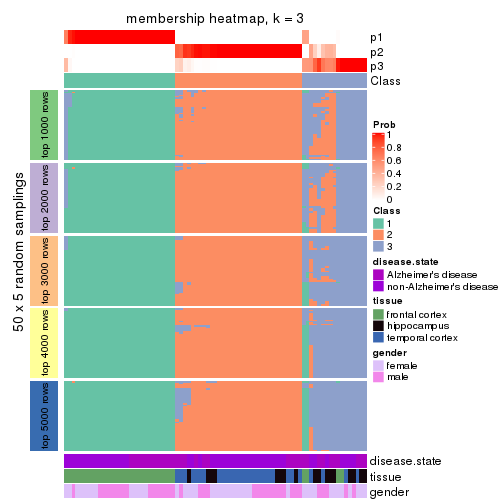
membership_heatmap(res, k = 4)
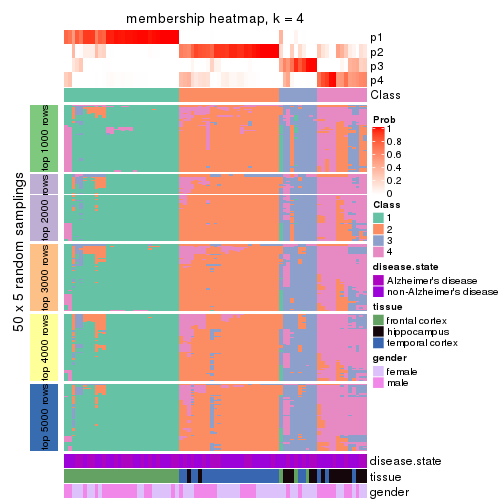
membership_heatmap(res, k = 5)
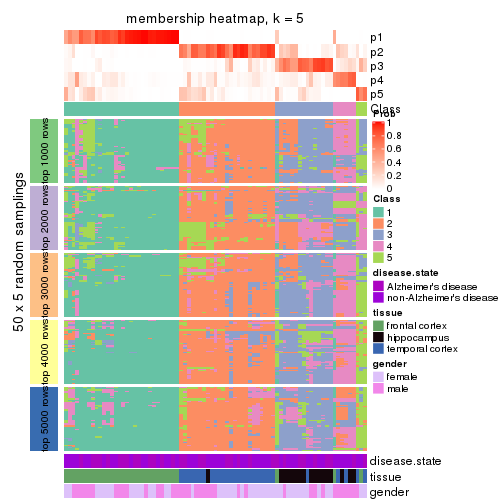
membership_heatmap(res, k = 6)
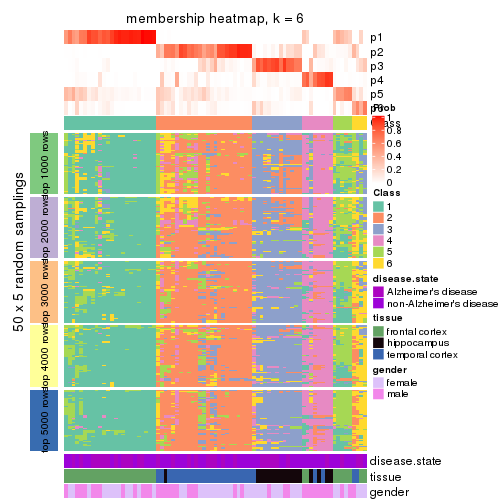
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
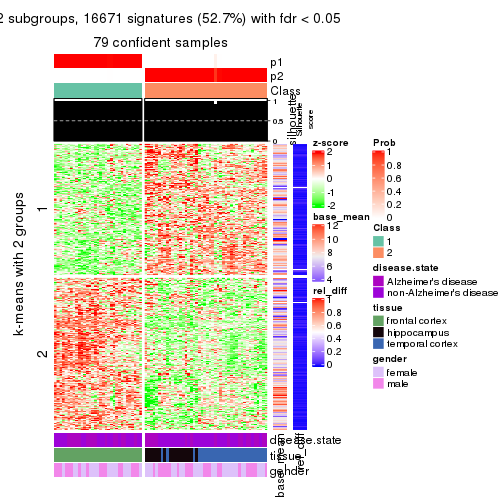
get_signatures(res, k = 3)
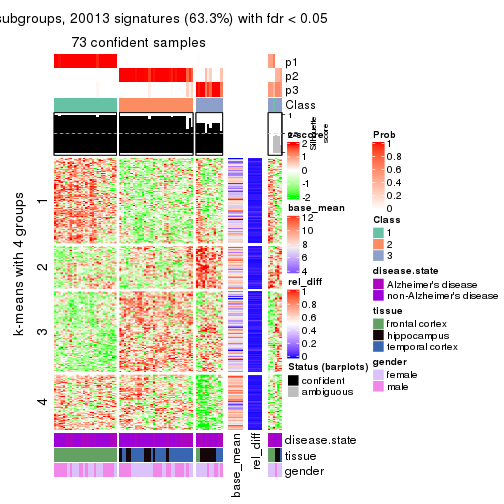
get_signatures(res, k = 4)
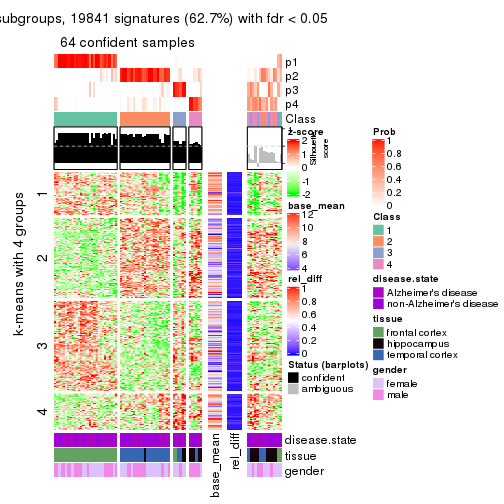
get_signatures(res, k = 5)
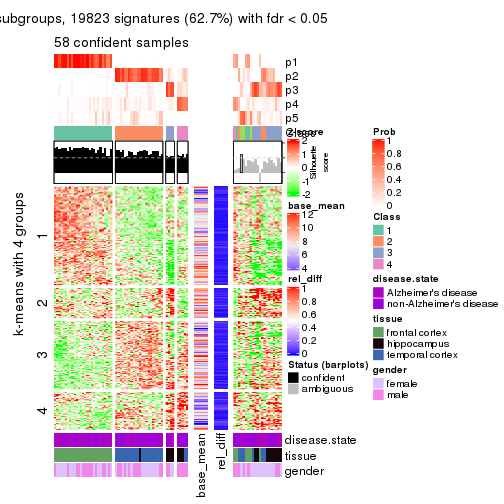
get_signatures(res, k = 6)
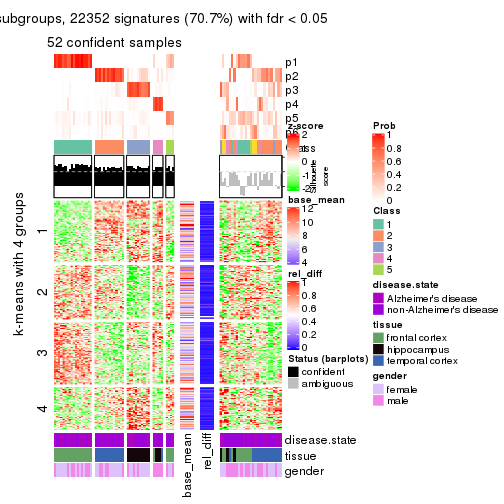
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
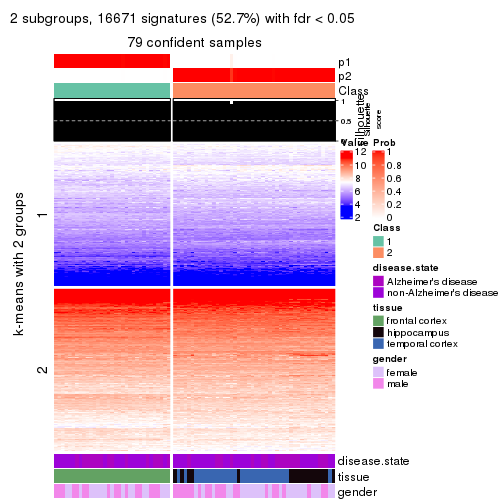
get_signatures(res, k = 3, scale_rows = FALSE)
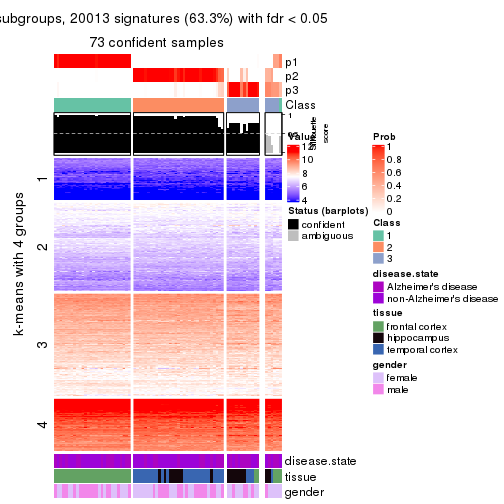
get_signatures(res, k = 4, scale_rows = FALSE)
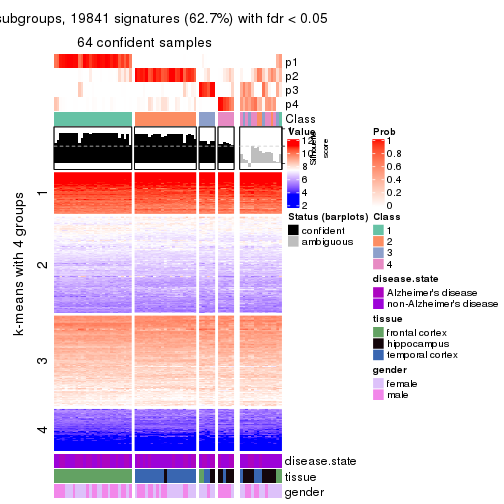
get_signatures(res, k = 5, scale_rows = FALSE)
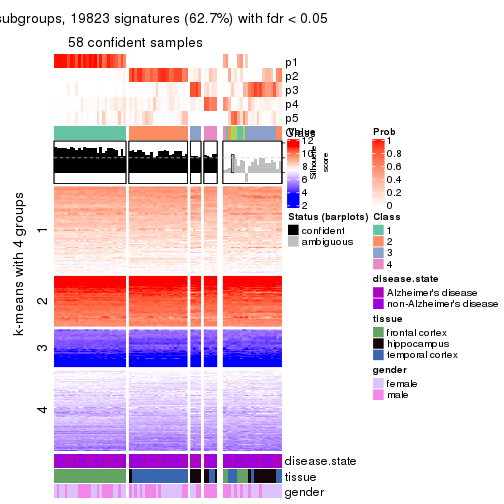
get_signatures(res, k = 6, scale_rows = FALSE)
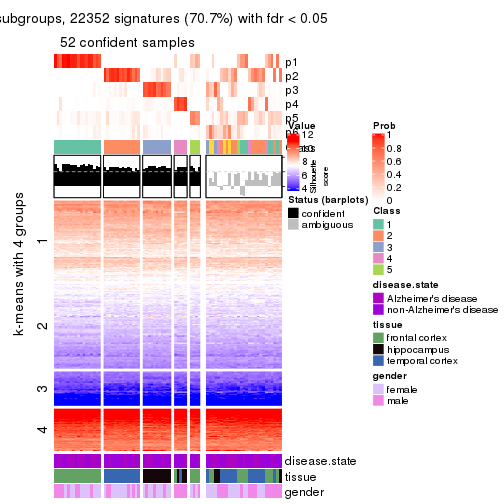
Compare the overlap of signatures from different k:
compare_signatures(res)
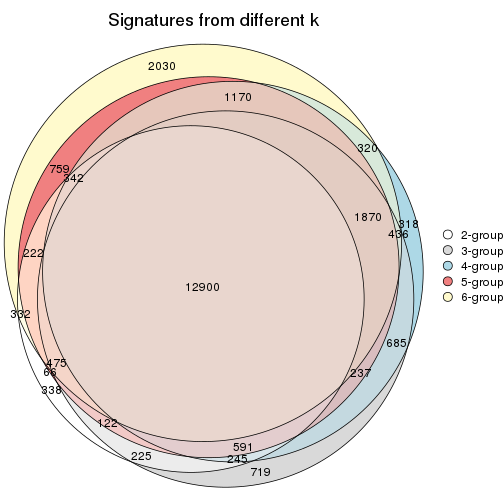
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
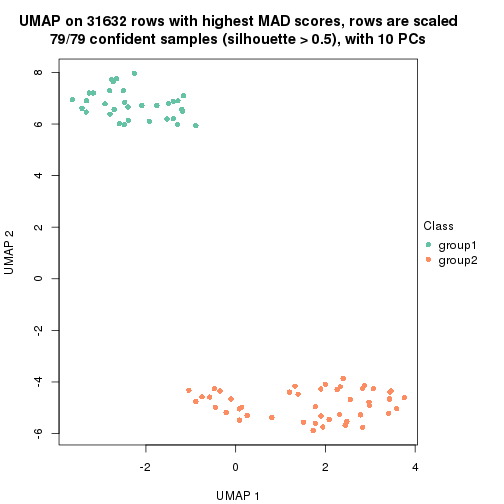
dimension_reduction(res, k = 3, method = "UMAP")
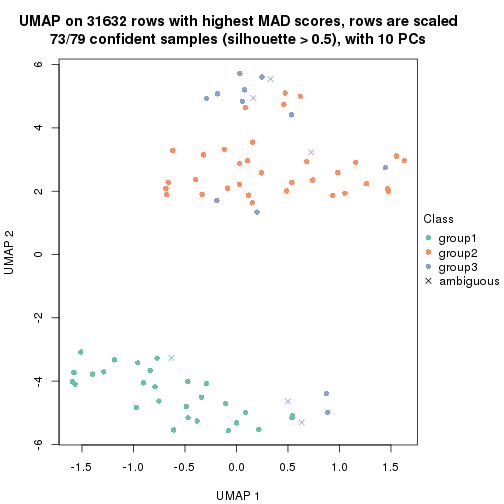
dimension_reduction(res, k = 4, method = "UMAP")
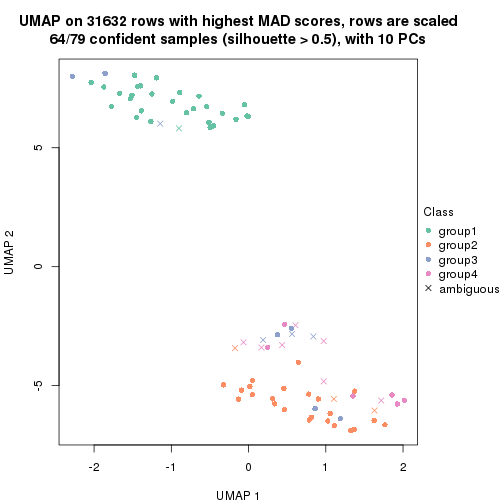
dimension_reduction(res, k = 5, method = "UMAP")
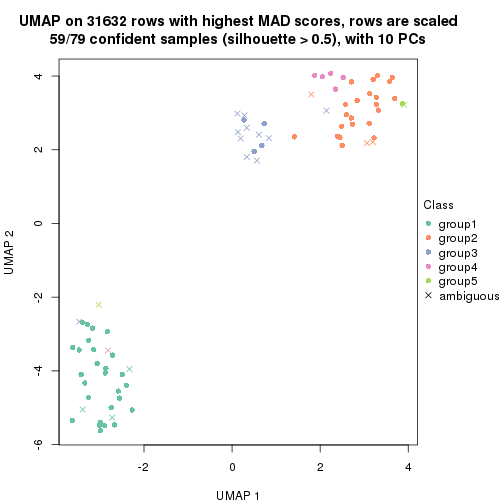
dimension_reduction(res, k = 6, method = "UMAP")
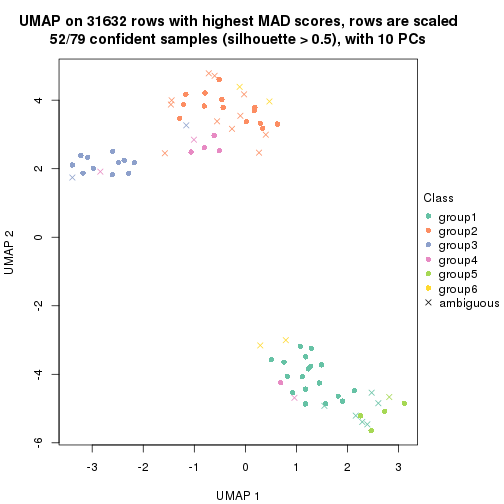
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
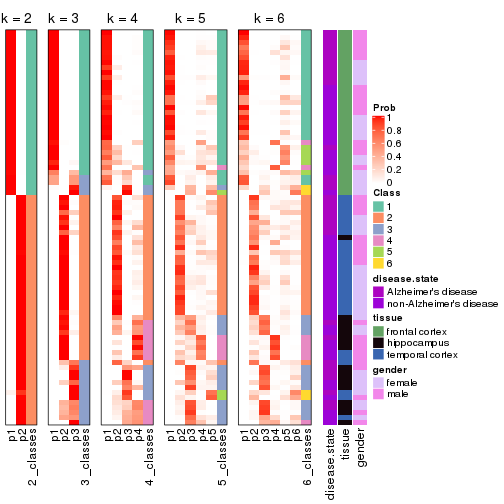
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> MAD:NMF 79 0.599 7.00e-18 0.9838 2
#> MAD:NMF 73 0.215 9.19e-16 0.3826 3
#> MAD:NMF 64 0.515 1.02e-17 0.1099 4
#> MAD:NMF 59 0.199 1.91e-17 0.1844 5
#> MAD:NMF 52 0.263 4.56e-17 0.0897 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "hclust"]
# you can also extract it by
# res = res_list["ATC:hclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'hclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
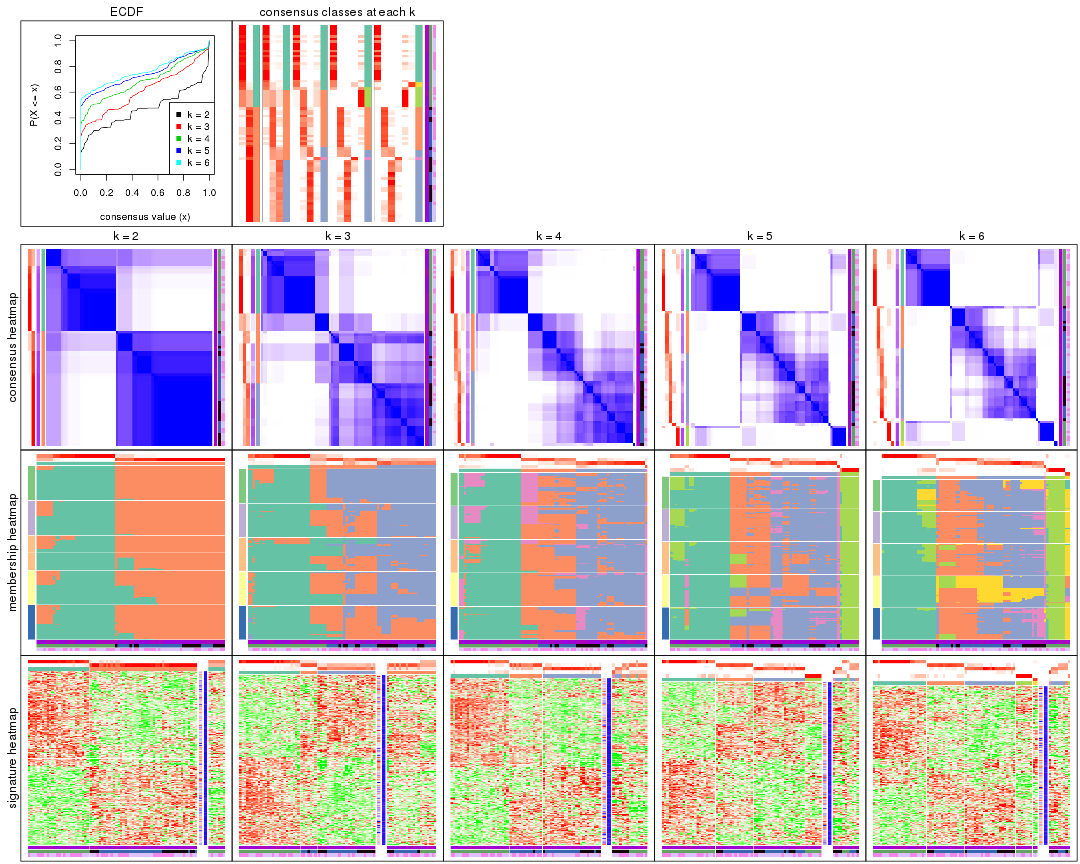
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
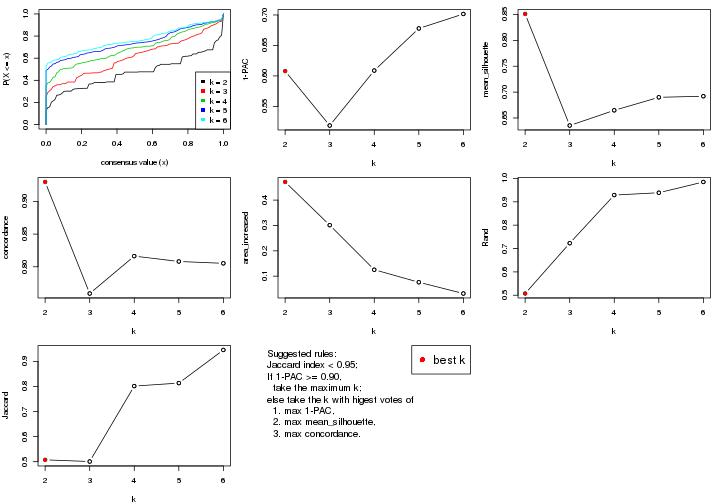
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.608 0.851 0.930 0.4716 0.507 0.507
#> 3 3 0.519 0.635 0.759 0.3012 0.723 0.501
#> 4 4 0.609 0.665 0.816 0.1254 0.929 0.801
#> 5 5 0.678 0.690 0.808 0.0759 0.939 0.813
#> 6 6 0.702 0.692 0.805 0.0315 0.985 0.945
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.940 0.000 1.000
#> GSM907859 2 0.7883 0.711 0.236 0.764
#> GSM907860 2 0.0000 0.940 0.000 1.000
#> GSM907854 2 0.0000 0.940 0.000 1.000
#> GSM907855 2 0.0000 0.940 0.000 1.000
#> GSM907856 2 0.0000 0.940 0.000 1.000
#> GSM907857 2 0.6048 0.829 0.148 0.852
#> GSM907825 2 0.0000 0.940 0.000 1.000
#> GSM907828 2 0.0376 0.939 0.004 0.996
#> GSM907832 2 0.3114 0.916 0.056 0.944
#> GSM907833 2 0.3114 0.916 0.056 0.944
#> GSM907834 2 0.0000 0.940 0.000 1.000
#> GSM907826 2 0.0000 0.940 0.000 1.000
#> GSM907827 2 0.0000 0.940 0.000 1.000
#> GSM907829 2 0.7883 0.711 0.236 0.764
#> GSM907830 2 0.0376 0.939 0.004 0.996
#> GSM907831 2 0.0000 0.940 0.000 1.000
#> GSM907792 1 0.0000 0.885 1.000 0.000
#> GSM907795 1 0.0000 0.885 1.000 0.000
#> GSM907801 1 0.0000 0.885 1.000 0.000
#> GSM907802 1 0.9635 0.450 0.612 0.388
#> GSM907804 1 0.9635 0.450 0.612 0.388
#> GSM907805 1 0.0000 0.885 1.000 0.000
#> GSM907806 1 0.1843 0.880 0.972 0.028
#> GSM907793 1 0.0000 0.885 1.000 0.000
#> GSM907794 1 0.1843 0.880 0.972 0.028
#> GSM907796 1 0.0000 0.885 1.000 0.000
#> GSM907797 1 0.4690 0.831 0.900 0.100
#> GSM907798 1 0.0000 0.885 1.000 0.000
#> GSM907799 1 0.0000 0.885 1.000 0.000
#> GSM907800 1 0.9635 0.450 0.612 0.388
#> GSM907803 1 0.1843 0.880 0.972 0.028
#> GSM907864 2 0.2603 0.922 0.044 0.956
#> GSM907865 2 0.2603 0.922 0.044 0.956
#> GSM907868 2 0.0000 0.940 0.000 1.000
#> GSM907869 2 0.0000 0.940 0.000 1.000
#> GSM907870 2 0.0000 0.940 0.000 1.000
#> GSM907861 2 0.0000 0.940 0.000 1.000
#> GSM907862 2 0.0000 0.940 0.000 1.000
#> GSM907863 2 0.0000 0.940 0.000 1.000
#> GSM907866 2 0.0000 0.940 0.000 1.000
#> GSM907867 2 0.0000 0.940 0.000 1.000
#> GSM907839 2 0.3114 0.916 0.056 0.944
#> GSM907840 2 0.0000 0.940 0.000 1.000
#> GSM907842 2 0.3114 0.916 0.056 0.944
#> GSM907843 2 0.7883 0.711 0.236 0.764
#> GSM907845 2 0.7883 0.711 0.236 0.764
#> GSM907846 2 0.7883 0.711 0.236 0.764
#> GSM907848 2 0.3114 0.916 0.056 0.944
#> GSM907851 2 0.7883 0.711 0.236 0.764
#> GSM907835 2 0.0000 0.940 0.000 1.000
#> GSM907836 2 0.0000 0.940 0.000 1.000
#> GSM907837 2 0.0000 0.940 0.000 1.000
#> GSM907838 2 0.0000 0.940 0.000 1.000
#> GSM907841 2 0.0000 0.940 0.000 1.000
#> GSM907844 2 0.0000 0.940 0.000 1.000
#> GSM907847 2 0.3114 0.916 0.056 0.944
#> GSM907849 2 0.7883 0.711 0.236 0.764
#> GSM907850 2 0.3114 0.916 0.056 0.944
#> GSM907852 2 0.0000 0.940 0.000 1.000
#> GSM907853 2 0.1184 0.934 0.016 0.984
#> GSM907807 1 0.0000 0.885 1.000 0.000
#> GSM907813 1 0.1633 0.881 0.976 0.024
#> GSM907814 1 0.0000 0.885 1.000 0.000
#> GSM907816 1 0.0000 0.885 1.000 0.000
#> GSM907818 1 0.6048 0.791 0.852 0.148
#> GSM907819 1 0.1843 0.880 0.972 0.028
#> GSM907820 1 0.9635 0.450 0.612 0.388
#> GSM907822 1 0.0376 0.885 0.996 0.004
#> GSM907823 1 0.0376 0.885 0.996 0.004
#> GSM907808 1 0.0000 0.885 1.000 0.000
#> GSM907809 1 0.0000 0.885 1.000 0.000
#> GSM907810 1 0.0000 0.885 1.000 0.000
#> GSM907811 1 0.9635 0.450 0.612 0.388
#> GSM907812 1 0.0000 0.885 1.000 0.000
#> GSM907815 1 0.4690 0.831 0.900 0.100
#> GSM907817 1 0.9635 0.450 0.612 0.388
#> GSM907821 1 0.2043 0.878 0.968 0.032
#> GSM907824 1 0.9635 0.450 0.612 0.388
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.4399 0.766 0.000 0.188 0.812
#> GSM907859 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907860 3 0.4974 0.818 0.000 0.236 0.764
#> GSM907854 3 0.4702 0.795 0.000 0.212 0.788
#> GSM907855 3 0.4399 0.766 0.000 0.188 0.812
#> GSM907856 3 0.4399 0.766 0.000 0.188 0.812
#> GSM907857 2 0.6308 -0.233 0.000 0.508 0.492
#> GSM907825 3 0.5859 0.890 0.000 0.344 0.656
#> GSM907828 2 0.6295 -0.620 0.000 0.528 0.472
#> GSM907832 2 0.3752 0.409 0.000 0.856 0.144
#> GSM907833 2 0.4121 0.375 0.000 0.832 0.168
#> GSM907834 3 0.5859 0.890 0.000 0.344 0.656
#> GSM907826 3 0.6180 0.839 0.000 0.416 0.584
#> GSM907827 3 0.5859 0.890 0.000 0.344 0.656
#> GSM907829 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907830 2 0.6291 -0.611 0.000 0.532 0.468
#> GSM907831 3 0.5859 0.890 0.000 0.344 0.656
#> GSM907792 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907802 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907804 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907805 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907806 1 0.4007 0.889 0.880 0.036 0.084
#> GSM907793 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907794 1 0.4007 0.889 0.880 0.036 0.084
#> GSM907796 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907797 1 0.6306 0.727 0.748 0.200 0.052
#> GSM907798 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907800 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907803 1 0.4007 0.889 0.880 0.036 0.084
#> GSM907864 2 0.4702 0.274 0.000 0.788 0.212
#> GSM907865 2 0.4702 0.274 0.000 0.788 0.212
#> GSM907868 3 0.5706 0.884 0.000 0.320 0.680
#> GSM907869 3 0.6215 0.805 0.000 0.428 0.572
#> GSM907870 2 0.6079 -0.381 0.000 0.612 0.388
#> GSM907861 3 0.6225 0.799 0.000 0.432 0.568
#> GSM907862 3 0.5678 0.883 0.000 0.316 0.684
#> GSM907863 3 0.5678 0.883 0.000 0.316 0.684
#> GSM907866 3 0.5397 0.858 0.000 0.280 0.720
#> GSM907867 3 0.6215 0.806 0.000 0.428 0.572
#> GSM907839 2 0.3752 0.409 0.000 0.856 0.144
#> GSM907840 3 0.6026 0.880 0.000 0.376 0.624
#> GSM907842 2 0.4002 0.388 0.000 0.840 0.160
#> GSM907843 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907845 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907846 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907848 2 0.4121 0.375 0.000 0.832 0.168
#> GSM907851 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907835 3 0.6180 0.839 0.000 0.416 0.584
#> GSM907836 3 0.6180 0.839 0.000 0.416 0.584
#> GSM907837 3 0.6026 0.880 0.000 0.376 0.624
#> GSM907838 3 0.6026 0.880 0.000 0.376 0.624
#> GSM907841 3 0.5810 0.890 0.000 0.336 0.664
#> GSM907844 3 0.6140 0.854 0.000 0.404 0.596
#> GSM907847 2 0.3752 0.409 0.000 0.856 0.144
#> GSM907849 2 0.4121 0.558 0.168 0.832 0.000
#> GSM907850 2 0.4002 0.388 0.000 0.840 0.160
#> GSM907852 3 0.6026 0.880 0.000 0.376 0.624
#> GSM907853 2 0.6286 -0.600 0.000 0.536 0.464
#> GSM907807 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907813 1 0.3765 0.893 0.888 0.028 0.084
#> GSM907814 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907816 1 0.0237 0.932 0.996 0.004 0.000
#> GSM907818 1 0.7478 0.642 0.692 0.192 0.116
#> GSM907819 1 0.4007 0.889 0.880 0.036 0.084
#> GSM907820 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907822 1 0.2584 0.912 0.928 0.008 0.064
#> GSM907823 1 0.2584 0.912 0.928 0.008 0.064
#> GSM907808 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907811 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907812 1 0.0000 0.933 1.000 0.000 0.000
#> GSM907815 1 0.6306 0.727 0.748 0.200 0.052
#> GSM907817 2 0.9335 0.145 0.376 0.456 0.168
#> GSM907821 1 0.4206 0.883 0.872 0.040 0.088
#> GSM907824 2 0.9335 0.145 0.376 0.456 0.168
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.4605 0.492 0.000 0.000 0.664 0.336
#> GSM907859 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907860 3 0.3801 0.642 0.000 0.000 0.780 0.220
#> GSM907854 3 0.4222 0.592 0.000 0.000 0.728 0.272
#> GSM907855 3 0.4605 0.492 0.000 0.000 0.664 0.336
#> GSM907856 3 0.4605 0.492 0.000 0.000 0.664 0.336
#> GSM907857 4 0.3945 0.000 0.000 0.216 0.004 0.780
#> GSM907825 3 0.1520 0.814 0.000 0.024 0.956 0.020
#> GSM907828 3 0.4222 0.544 0.000 0.272 0.728 0.000
#> GSM907832 2 0.4661 0.564 0.000 0.652 0.348 0.000
#> GSM907833 2 0.4830 0.503 0.000 0.608 0.392 0.000
#> GSM907834 3 0.1520 0.814 0.000 0.024 0.956 0.020
#> GSM907826 3 0.2530 0.773 0.000 0.112 0.888 0.000
#> GSM907827 3 0.1520 0.814 0.000 0.024 0.956 0.020
#> GSM907829 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907830 3 0.4250 0.536 0.000 0.276 0.724 0.000
#> GSM907831 3 0.1520 0.814 0.000 0.024 0.956 0.020
#> GSM907792 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907802 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907804 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907805 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907806 1 0.5771 0.702 0.712 0.144 0.000 0.144
#> GSM907793 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907794 1 0.5862 0.695 0.704 0.148 0.000 0.148
#> GSM907796 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907797 1 0.4675 0.604 0.736 0.020 0.000 0.244
#> GSM907798 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907799 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907800 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907803 1 0.5862 0.695 0.704 0.148 0.000 0.148
#> GSM907864 2 0.4916 0.416 0.000 0.576 0.424 0.000
#> GSM907865 2 0.4916 0.416 0.000 0.576 0.424 0.000
#> GSM907868 3 0.1940 0.777 0.000 0.000 0.924 0.076
#> GSM907869 3 0.3757 0.745 0.000 0.152 0.828 0.020
#> GSM907870 3 0.4543 0.400 0.000 0.324 0.676 0.000
#> GSM907861 3 0.3806 0.741 0.000 0.156 0.824 0.020
#> GSM907862 3 0.2081 0.773 0.000 0.000 0.916 0.084
#> GSM907863 3 0.2081 0.773 0.000 0.000 0.916 0.084
#> GSM907866 3 0.2704 0.735 0.000 0.000 0.876 0.124
#> GSM907867 3 0.4286 0.766 0.000 0.136 0.812 0.052
#> GSM907839 2 0.4605 0.576 0.000 0.664 0.336 0.000
#> GSM907840 3 0.1211 0.814 0.000 0.040 0.960 0.000
#> GSM907842 2 0.4790 0.524 0.000 0.620 0.380 0.000
#> GSM907843 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907845 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907846 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907848 2 0.4830 0.503 0.000 0.608 0.392 0.000
#> GSM907851 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907835 3 0.2589 0.770 0.000 0.116 0.884 0.000
#> GSM907836 3 0.2589 0.770 0.000 0.116 0.884 0.000
#> GSM907837 3 0.1211 0.814 0.000 0.040 0.960 0.000
#> GSM907838 3 0.1211 0.814 0.000 0.040 0.960 0.000
#> GSM907841 3 0.2443 0.802 0.000 0.024 0.916 0.060
#> GSM907844 3 0.1867 0.799 0.000 0.072 0.928 0.000
#> GSM907847 2 0.4624 0.572 0.000 0.660 0.340 0.000
#> GSM907849 2 0.2760 0.616 0.000 0.872 0.128 0.000
#> GSM907850 2 0.4790 0.524 0.000 0.620 0.380 0.000
#> GSM907852 3 0.1211 0.814 0.000 0.040 0.960 0.000
#> GSM907853 3 0.4134 0.567 0.000 0.260 0.740 0.000
#> GSM907807 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907813 1 0.5321 0.730 0.748 0.112 0.000 0.140
#> GSM907814 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907816 1 0.0937 0.853 0.976 0.012 0.000 0.012
#> GSM907818 1 0.7443 0.248 0.436 0.392 0.000 0.172
#> GSM907819 1 0.5862 0.695 0.704 0.148 0.000 0.148
#> GSM907820 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907822 1 0.2908 0.822 0.896 0.040 0.000 0.064
#> GSM907823 1 0.2908 0.822 0.896 0.040 0.000 0.064
#> GSM907808 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907811 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907812 1 0.0000 0.860 1.000 0.000 0.000 0.000
#> GSM907815 1 0.4675 0.604 0.736 0.020 0.000 0.244
#> GSM907817 2 0.5109 0.417 0.052 0.736 0.000 0.212
#> GSM907821 1 0.5951 0.687 0.696 0.152 0.000 0.152
#> GSM907824 2 0.5109 0.417 0.052 0.736 0.000 0.212
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.3684 0.4414 0.000 0.000 0.720 0.280 0.000
#> GSM907859 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907860 3 0.2773 0.6024 0.000 0.000 0.836 0.164 0.000
#> GSM907854 3 0.3242 0.5354 0.000 0.000 0.784 0.216 0.000
#> GSM907855 3 0.3684 0.4414 0.000 0.000 0.720 0.280 0.000
#> GSM907856 3 0.3684 0.4414 0.000 0.000 0.720 0.280 0.000
#> GSM907857 4 0.1121 0.0000 0.000 0.000 0.044 0.956 0.000
#> GSM907825 3 0.1410 0.7486 0.000 0.060 0.940 0.000 0.000
#> GSM907828 3 0.4304 0.2611 0.000 0.484 0.516 0.000 0.000
#> GSM907832 2 0.2286 0.7683 0.000 0.888 0.108 0.000 0.004
#> GSM907833 2 0.2806 0.7408 0.000 0.844 0.152 0.000 0.004
#> GSM907834 3 0.2020 0.7516 0.000 0.100 0.900 0.000 0.000
#> GSM907826 3 0.3816 0.6349 0.000 0.304 0.696 0.000 0.000
#> GSM907827 3 0.1410 0.7486 0.000 0.060 0.940 0.000 0.000
#> GSM907829 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907830 3 0.4305 0.2502 0.000 0.488 0.512 0.000 0.000
#> GSM907831 3 0.1410 0.7486 0.000 0.060 0.940 0.000 0.000
#> GSM907792 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907804 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907805 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907806 1 0.3837 0.6275 0.692 0.000 0.000 0.000 0.308
#> GSM907793 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907794 1 0.3876 0.6152 0.684 0.000 0.000 0.000 0.316
#> GSM907796 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907797 1 0.5334 0.4371 0.644 0.020 0.000 0.292 0.044
#> GSM907798 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907799 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907803 1 0.3876 0.6152 0.684 0.000 0.000 0.000 0.316
#> GSM907864 2 0.2690 0.6973 0.000 0.844 0.156 0.000 0.000
#> GSM907865 2 0.2690 0.6973 0.000 0.844 0.156 0.000 0.000
#> GSM907868 3 0.1981 0.7149 0.000 0.028 0.924 0.048 0.000
#> GSM907869 3 0.3336 0.6704 0.000 0.228 0.772 0.000 0.000
#> GSM907870 2 0.4273 -0.0473 0.000 0.552 0.448 0.000 0.000
#> GSM907861 3 0.3366 0.6669 0.000 0.232 0.768 0.000 0.000
#> GSM907862 3 0.1965 0.7112 0.000 0.024 0.924 0.052 0.000
#> GSM907863 3 0.1965 0.7112 0.000 0.024 0.924 0.052 0.000
#> GSM907866 3 0.1544 0.6795 0.000 0.000 0.932 0.068 0.000
#> GSM907867 3 0.3805 0.7015 0.000 0.184 0.784 0.032 0.000
#> GSM907839 2 0.2124 0.7712 0.000 0.900 0.096 0.000 0.004
#> GSM907840 3 0.3366 0.7068 0.000 0.232 0.768 0.000 0.000
#> GSM907842 2 0.2674 0.7518 0.000 0.856 0.140 0.000 0.004
#> GSM907843 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907845 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907846 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907848 2 0.2806 0.7408 0.000 0.844 0.152 0.000 0.004
#> GSM907851 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907835 3 0.3837 0.6304 0.000 0.308 0.692 0.000 0.000
#> GSM907836 3 0.3837 0.6304 0.000 0.308 0.692 0.000 0.000
#> GSM907837 3 0.3366 0.7068 0.000 0.232 0.768 0.000 0.000
#> GSM907838 3 0.3366 0.7068 0.000 0.232 0.768 0.000 0.000
#> GSM907841 3 0.2905 0.7494 0.000 0.096 0.868 0.036 0.000
#> GSM907844 3 0.3210 0.7155 0.000 0.212 0.788 0.000 0.000
#> GSM907847 2 0.2179 0.7708 0.000 0.896 0.100 0.000 0.004
#> GSM907849 2 0.2929 0.7155 0.000 0.820 0.000 0.000 0.180
#> GSM907850 2 0.2674 0.7518 0.000 0.856 0.140 0.000 0.004
#> GSM907852 3 0.3366 0.7068 0.000 0.232 0.768 0.000 0.000
#> GSM907853 3 0.4297 0.3003 0.000 0.472 0.528 0.000 0.000
#> GSM907807 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.3612 0.6747 0.732 0.000 0.000 0.000 0.268
#> GSM907814 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0963 0.8508 0.964 0.000 0.000 0.000 0.036
#> GSM907818 5 0.4192 0.1055 0.404 0.000 0.000 0.000 0.596
#> GSM907819 1 0.3876 0.6152 0.684 0.000 0.000 0.000 0.316
#> GSM907820 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907822 1 0.2280 0.8077 0.880 0.000 0.000 0.000 0.120
#> GSM907823 1 0.2280 0.8077 0.880 0.000 0.000 0.000 0.120
#> GSM907808 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907811 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907812 1 0.0000 0.8628 1.000 0.000 0.000 0.000 0.000
#> GSM907815 1 0.5334 0.4371 0.644 0.020 0.000 0.292 0.044
#> GSM907817 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
#> GSM907821 1 0.3932 0.5969 0.672 0.000 0.000 0.000 0.328
#> GSM907824 5 0.0290 0.8960 0.000 0.008 0.000 0.000 0.992
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.3684 0.455 0.000 0.000 0.628 0.372 0.000 0.000
#> GSM907859 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907860 3 0.3198 0.592 0.000 0.000 0.740 0.260 0.000 0.000
#> GSM907854 3 0.3446 0.544 0.000 0.000 0.692 0.308 0.000 0.000
#> GSM907855 3 0.3684 0.455 0.000 0.000 0.628 0.372 0.000 0.000
#> GSM907856 3 0.3684 0.455 0.000 0.000 0.628 0.372 0.000 0.000
#> GSM907857 4 0.2092 0.000 0.000 0.000 0.000 0.876 0.000 0.124
#> GSM907825 3 0.0000 0.727 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907828 3 0.4284 0.299 0.000 0.440 0.544 0.012 0.000 0.004
#> GSM907832 2 0.1806 0.761 0.000 0.908 0.088 0.000 0.004 0.000
#> GSM907833 2 0.2320 0.748 0.000 0.864 0.132 0.000 0.004 0.000
#> GSM907834 3 0.0937 0.729 0.000 0.040 0.960 0.000 0.000 0.000
#> GSM907826 3 0.3633 0.639 0.000 0.252 0.732 0.012 0.000 0.004
#> GSM907827 3 0.0000 0.727 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907829 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907830 3 0.4289 0.290 0.000 0.444 0.540 0.012 0.000 0.004
#> GSM907831 3 0.0000 0.727 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907792 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907804 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907805 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907806 1 0.4829 0.566 0.612 0.000 0.000 0.000 0.308 0.080
#> GSM907793 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907794 1 0.4859 0.554 0.604 0.000 0.000 0.000 0.316 0.080
#> GSM907796 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907797 6 0.1644 1.000 0.076 0.000 0.000 0.000 0.004 0.920
#> GSM907798 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907799 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907803 1 0.4859 0.554 0.604 0.000 0.000 0.000 0.316 0.080
#> GSM907864 2 0.2362 0.705 0.000 0.860 0.136 0.000 0.000 0.004
#> GSM907865 2 0.2362 0.705 0.000 0.860 0.136 0.000 0.000 0.004
#> GSM907868 3 0.2100 0.697 0.000 0.004 0.884 0.112 0.000 0.000
#> GSM907869 3 0.3073 0.640 0.000 0.204 0.788 0.008 0.000 0.000
#> GSM907870 2 0.4393 -0.140 0.000 0.500 0.480 0.016 0.000 0.004
#> GSM907861 3 0.3103 0.638 0.000 0.208 0.784 0.008 0.000 0.000
#> GSM907862 3 0.2234 0.692 0.000 0.004 0.872 0.124 0.000 0.000
#> GSM907863 3 0.2234 0.692 0.000 0.004 0.872 0.124 0.000 0.000
#> GSM907866 3 0.2454 0.669 0.000 0.000 0.840 0.160 0.000 0.000
#> GSM907867 3 0.3481 0.662 0.000 0.160 0.792 0.048 0.000 0.000
#> GSM907839 2 0.1956 0.761 0.000 0.908 0.080 0.000 0.004 0.008
#> GSM907840 3 0.3178 0.701 0.000 0.176 0.804 0.016 0.000 0.004
#> GSM907842 2 0.2191 0.755 0.000 0.876 0.120 0.000 0.004 0.000
#> GSM907843 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907845 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907846 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907848 2 0.2320 0.748 0.000 0.864 0.132 0.000 0.004 0.000
#> GSM907851 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907835 3 0.3656 0.635 0.000 0.256 0.728 0.012 0.000 0.004
#> GSM907836 3 0.3656 0.635 0.000 0.256 0.728 0.012 0.000 0.004
#> GSM907837 3 0.3178 0.701 0.000 0.176 0.804 0.016 0.000 0.004
#> GSM907838 3 0.3178 0.701 0.000 0.176 0.804 0.016 0.000 0.004
#> GSM907841 3 0.2250 0.723 0.000 0.040 0.896 0.064 0.000 0.000
#> GSM907844 3 0.2805 0.709 0.000 0.160 0.828 0.012 0.000 0.000
#> GSM907847 2 0.1700 0.761 0.000 0.916 0.080 0.000 0.004 0.000
#> GSM907849 2 0.2814 0.710 0.000 0.820 0.000 0.000 0.172 0.008
#> GSM907850 2 0.2191 0.755 0.000 0.876 0.120 0.000 0.004 0.000
#> GSM907852 3 0.3178 0.701 0.000 0.176 0.804 0.016 0.000 0.004
#> GSM907853 3 0.4293 0.298 0.000 0.448 0.536 0.012 0.000 0.004
#> GSM907807 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.4654 0.618 0.652 0.000 0.000 0.000 0.268 0.080
#> GSM907814 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0865 0.830 0.964 0.000 0.000 0.000 0.036 0.000
#> GSM907818 5 0.4672 0.190 0.348 0.000 0.000 0.000 0.596 0.056
#> GSM907819 1 0.4859 0.554 0.604 0.000 0.000 0.000 0.316 0.080
#> GSM907820 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907822 1 0.3544 0.742 0.800 0.000 0.000 0.000 0.120 0.080
#> GSM907823 1 0.3544 0.742 0.800 0.000 0.000 0.000 0.120 0.080
#> GSM907808 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907812 1 0.0000 0.845 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907815 6 0.1644 1.000 0.076 0.000 0.000 0.000 0.004 0.920
#> GSM907817 5 0.0000 0.901 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907821 1 0.4900 0.533 0.592 0.000 0.000 0.000 0.328 0.080
#> GSM907824 5 0.0146 0.897 0.000 0.000 0.000 0.000 0.996 0.004
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
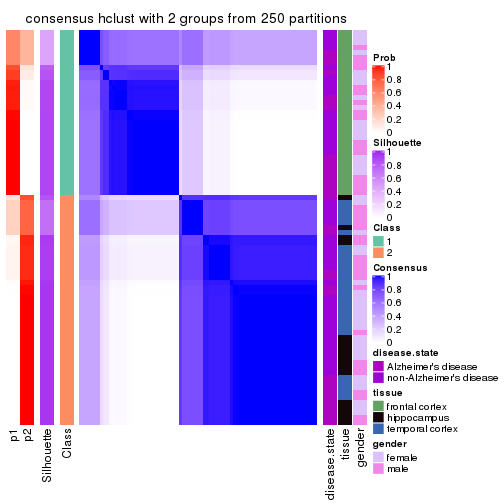
consensus_heatmap(res, k = 3)
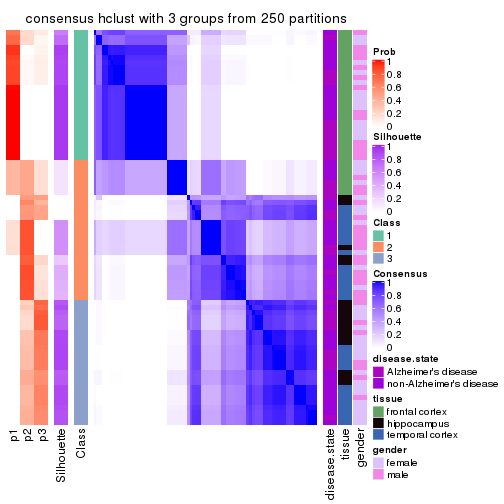
consensus_heatmap(res, k = 4)
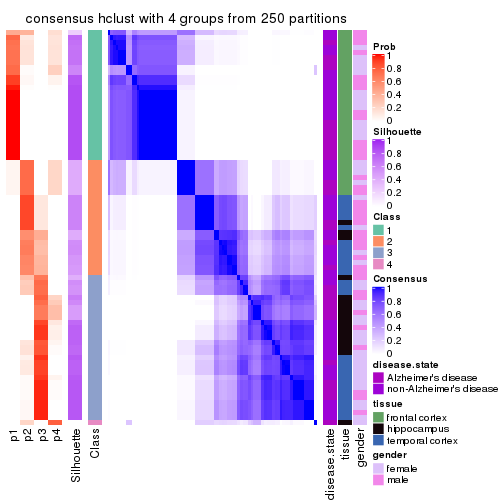
consensus_heatmap(res, k = 5)
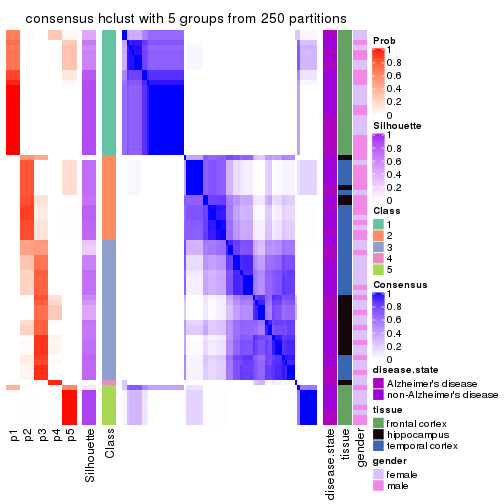
consensus_heatmap(res, k = 6)
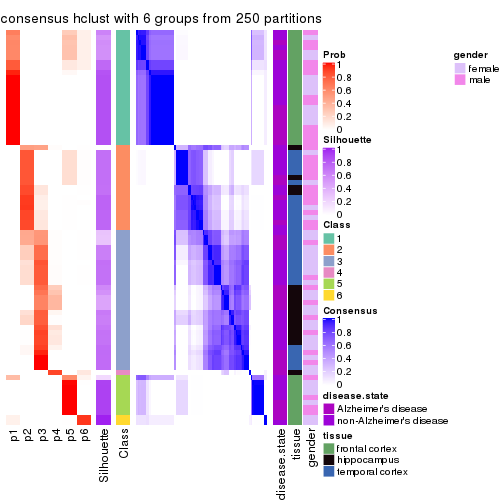
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
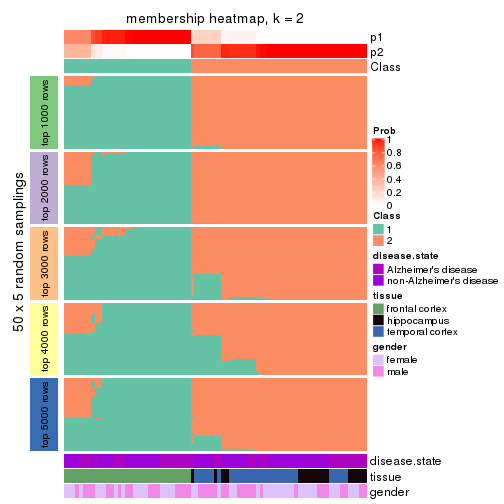
membership_heatmap(res, k = 3)
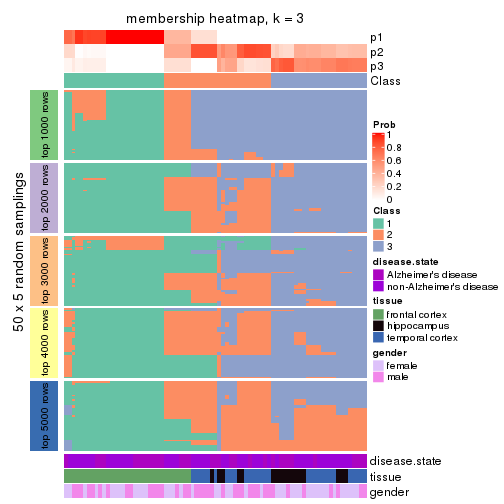
membership_heatmap(res, k = 4)
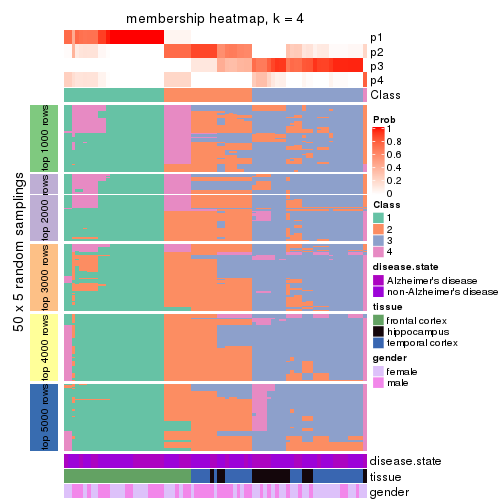
membership_heatmap(res, k = 5)
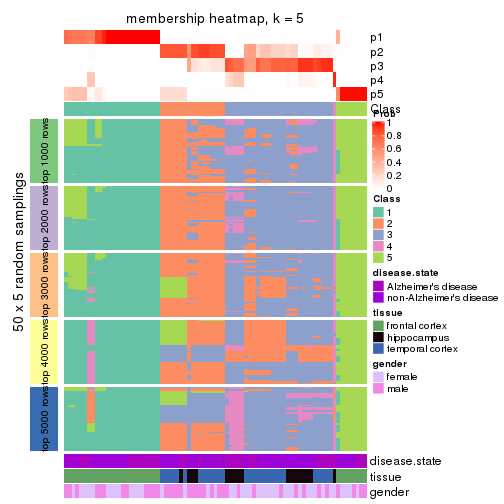
membership_heatmap(res, k = 6)
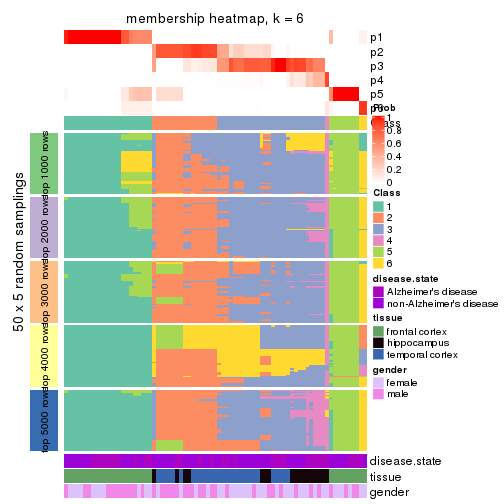
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
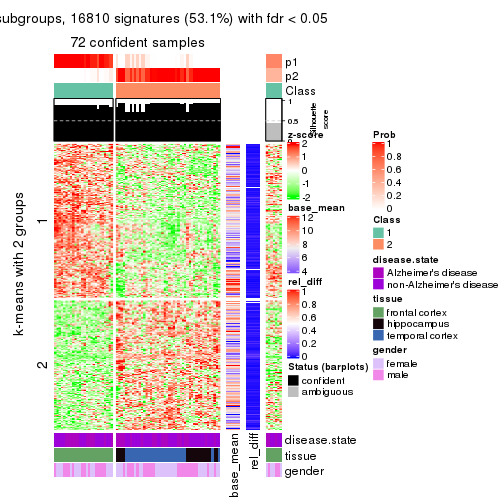
get_signatures(res, k = 3)
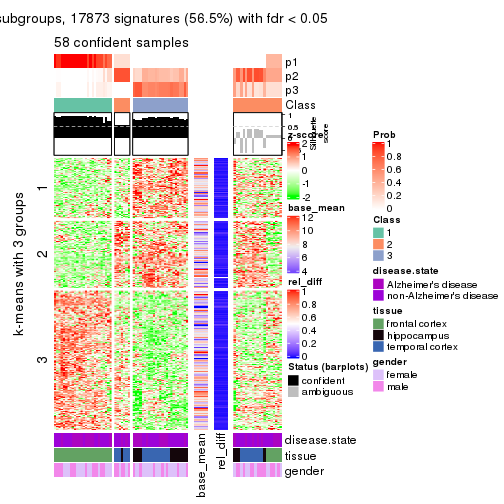
get_signatures(res, k = 4)
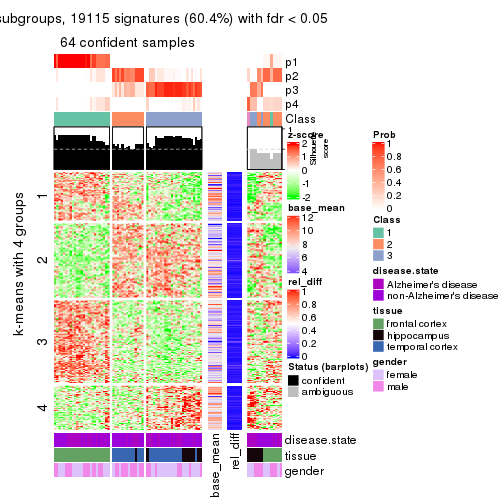
get_signatures(res, k = 5)
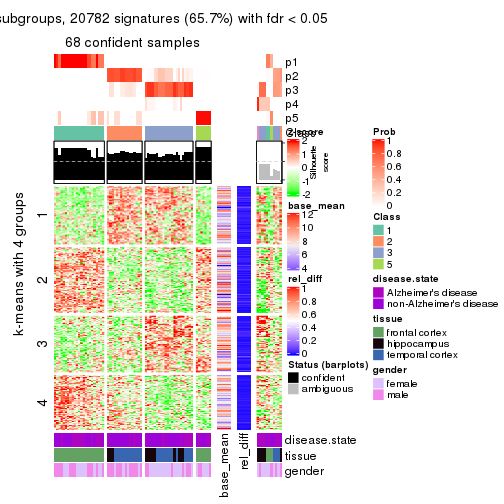
get_signatures(res, k = 6)
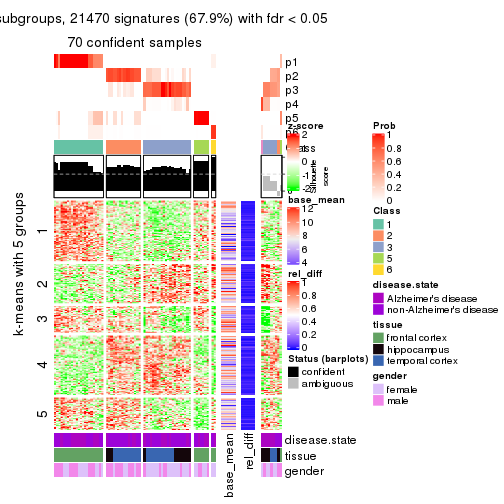
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
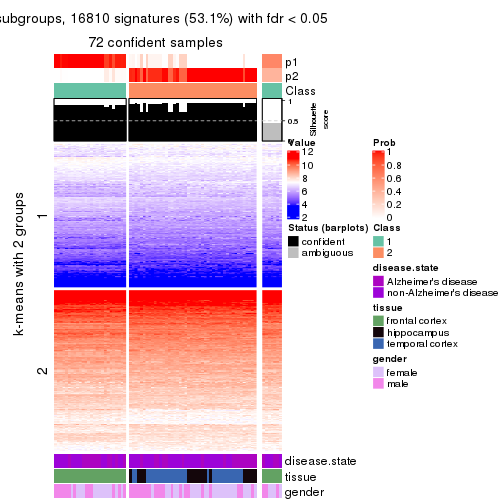
get_signatures(res, k = 3, scale_rows = FALSE)
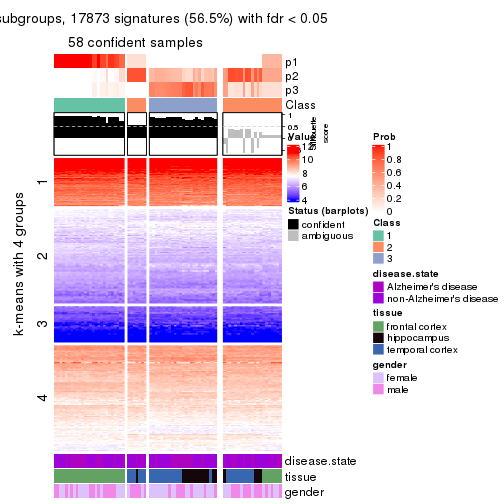
get_signatures(res, k = 4, scale_rows = FALSE)
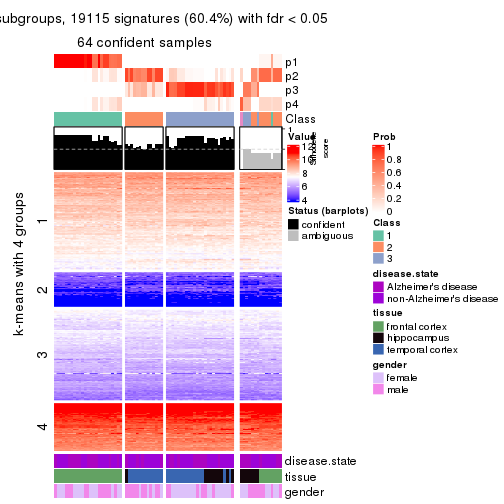
get_signatures(res, k = 5, scale_rows = FALSE)
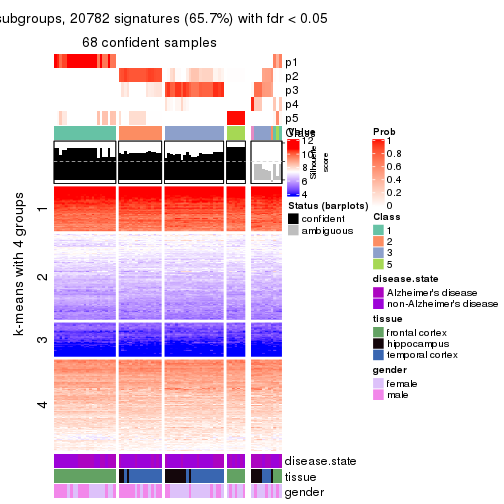
get_signatures(res, k = 6, scale_rows = FALSE)
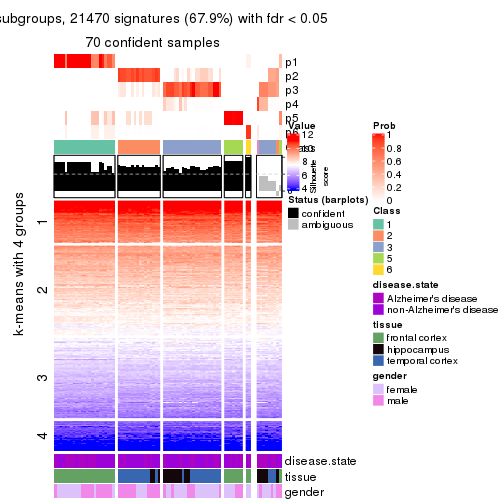
Compare the overlap of signatures from different k:
compare_signatures(res)
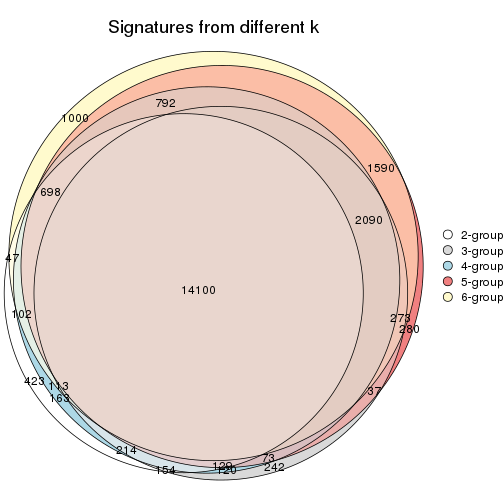
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
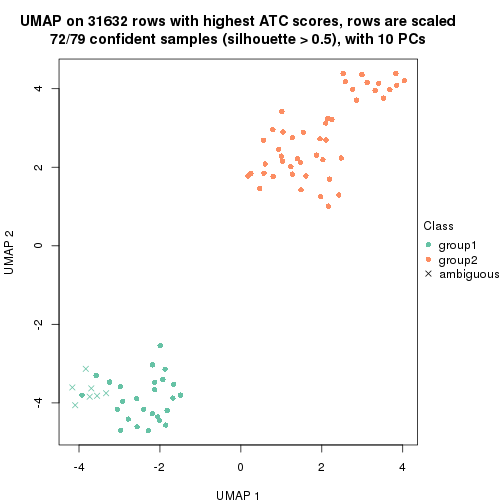
dimension_reduction(res, k = 3, method = "UMAP")
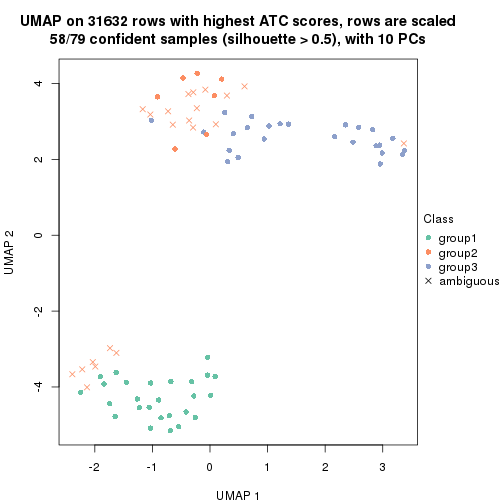
dimension_reduction(res, k = 4, method = "UMAP")
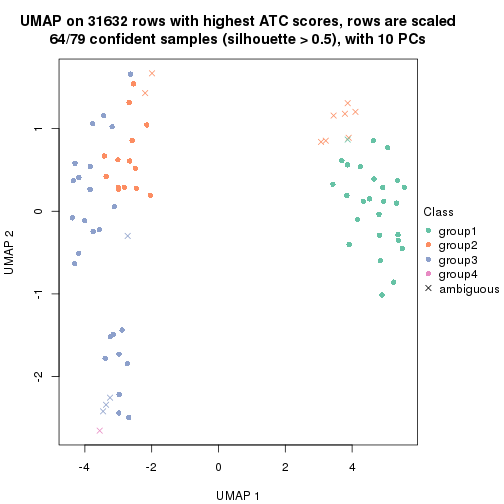
dimension_reduction(res, k = 5, method = "UMAP")
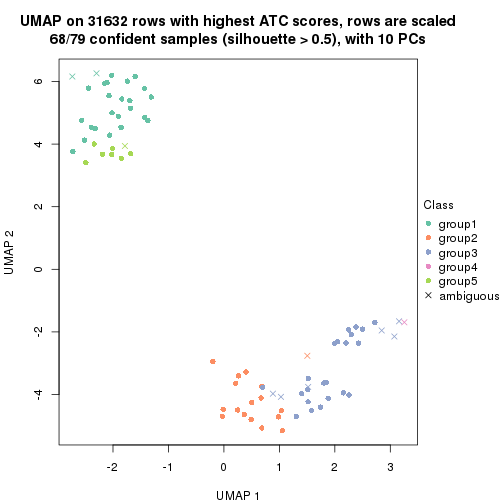
dimension_reduction(res, k = 6, method = "UMAP")
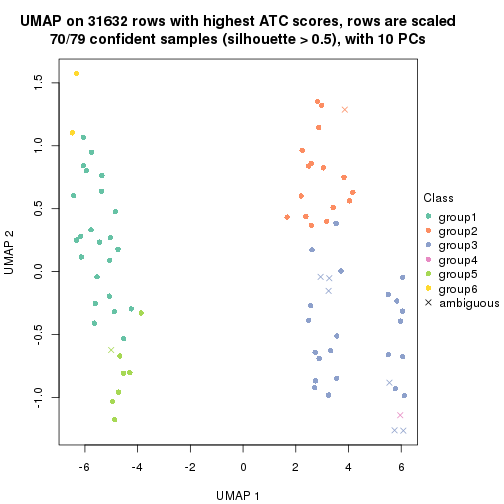
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
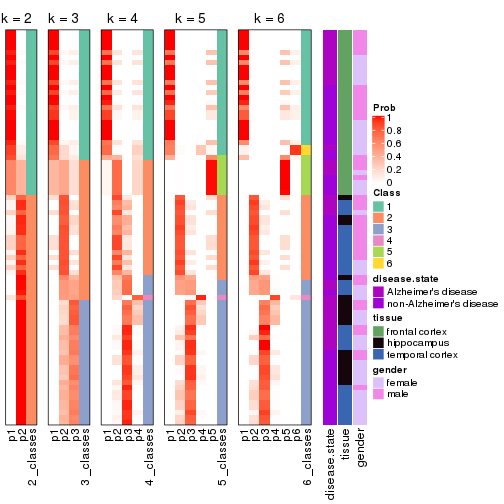
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:hclust 72 0.607 2.32e-16 0.9130 2
#> ATC:hclust 58 0.692 7.96e-13 0.0773 3
#> ATC:hclust 64 0.453 1.84e-14 0.0310 4
#> ATC:hclust 68 0.474 1.77e-13 0.0339 5
#> ATC:hclust 70 0.619 8.27e-13 0.0323 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "kmeans"]
# you can also extract it by
# res = res_list["ATC:kmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'kmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
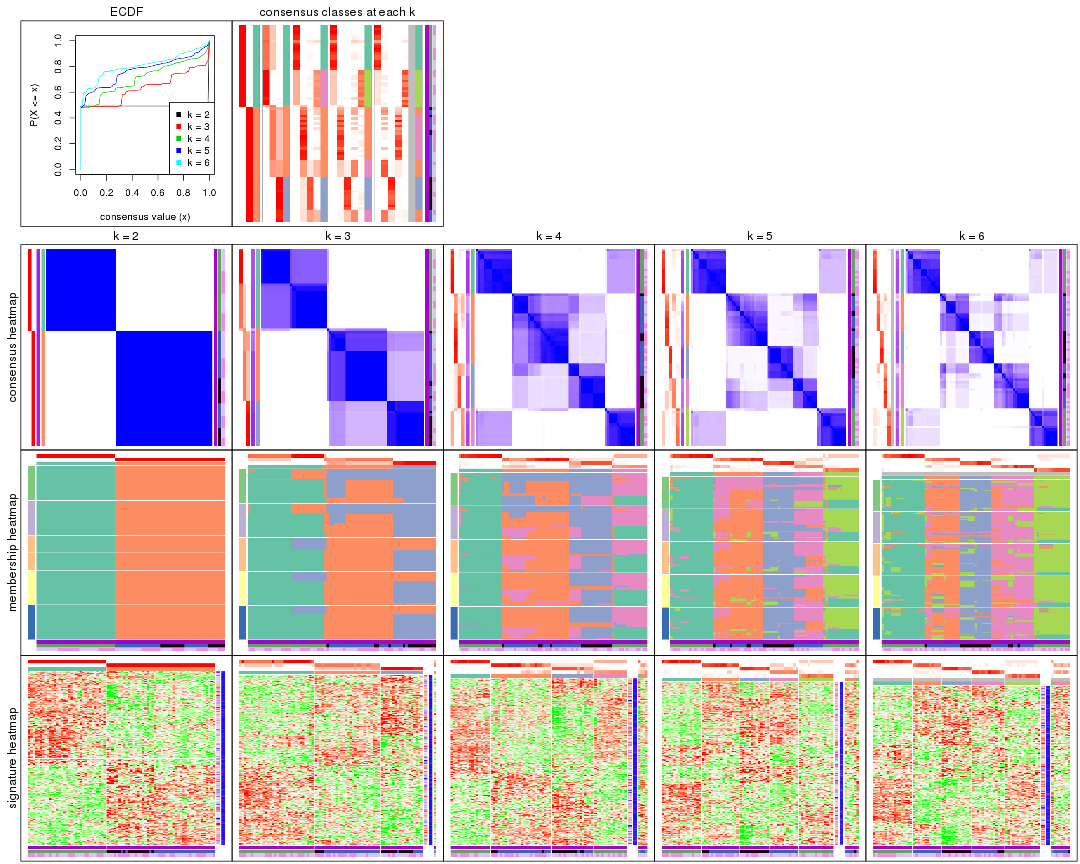
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
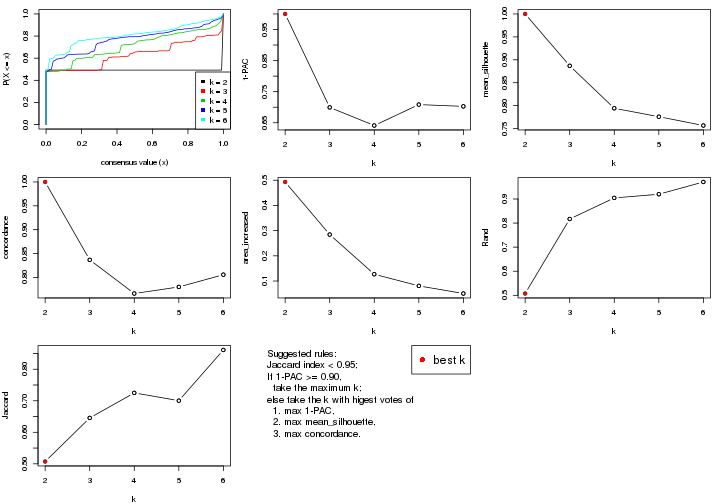
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 1.000 1.000 0.4932 0.507 0.507
#> 3 3 0.699 0.887 0.837 0.2844 0.817 0.646
#> 4 4 0.641 0.794 0.766 0.1269 0.905 0.725
#> 5 5 0.708 0.776 0.780 0.0807 0.920 0.700
#> 6 6 0.703 0.757 0.806 0.0504 0.971 0.861
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0 1 0 1
#> GSM907859 2 0 1 0 1
#> GSM907860 2 0 1 0 1
#> GSM907854 2 0 1 0 1
#> GSM907855 2 0 1 0 1
#> GSM907856 2 0 1 0 1
#> GSM907857 2 0 1 0 1
#> GSM907825 2 0 1 0 1
#> GSM907828 2 0 1 0 1
#> GSM907832 2 0 1 0 1
#> GSM907833 2 0 1 0 1
#> GSM907834 2 0 1 0 1
#> GSM907826 2 0 1 0 1
#> GSM907827 2 0 1 0 1
#> GSM907829 2 0 1 0 1
#> GSM907830 2 0 1 0 1
#> GSM907831 2 0 1 0 1
#> GSM907792 1 0 1 1 0
#> GSM907795 1 0 1 1 0
#> GSM907801 1 0 1 1 0
#> GSM907802 1 0 1 1 0
#> GSM907804 1 0 1 1 0
#> GSM907805 1 0 1 1 0
#> GSM907806 1 0 1 1 0
#> GSM907793 1 0 1 1 0
#> GSM907794 1 0 1 1 0
#> GSM907796 1 0 1 1 0
#> GSM907797 1 0 1 1 0
#> GSM907798 1 0 1 1 0
#> GSM907799 1 0 1 1 0
#> GSM907800 1 0 1 1 0
#> GSM907803 1 0 1 1 0
#> GSM907864 2 0 1 0 1
#> GSM907865 2 0 1 0 1
#> GSM907868 2 0 1 0 1
#> GSM907869 2 0 1 0 1
#> GSM907870 2 0 1 0 1
#> GSM907861 2 0 1 0 1
#> GSM907862 2 0 1 0 1
#> GSM907863 2 0 1 0 1
#> GSM907866 2 0 1 0 1
#> GSM907867 2 0 1 0 1
#> GSM907839 2 0 1 0 1
#> GSM907840 2 0 1 0 1
#> GSM907842 2 0 1 0 1
#> GSM907843 2 0 1 0 1
#> GSM907845 2 0 1 0 1
#> GSM907846 2 0 1 0 1
#> GSM907848 2 0 1 0 1
#> GSM907851 2 0 1 0 1
#> GSM907835 2 0 1 0 1
#> GSM907836 2 0 1 0 1
#> GSM907837 2 0 1 0 1
#> GSM907838 2 0 1 0 1
#> GSM907841 2 0 1 0 1
#> GSM907844 2 0 1 0 1
#> GSM907847 2 0 1 0 1
#> GSM907849 2 0 1 0 1
#> GSM907850 2 0 1 0 1
#> GSM907852 2 0 1 0 1
#> GSM907853 2 0 1 0 1
#> GSM907807 1 0 1 1 0
#> GSM907813 1 0 1 1 0
#> GSM907814 1 0 1 1 0
#> GSM907816 1 0 1 1 0
#> GSM907818 1 0 1 1 0
#> GSM907819 1 0 1 1 0
#> GSM907820 1 0 1 1 0
#> GSM907822 1 0 1 1 0
#> GSM907823 1 0 1 1 0
#> GSM907808 1 0 1 1 0
#> GSM907809 1 0 1 1 0
#> GSM907810 1 0 1 1 0
#> GSM907811 1 0 1 1 0
#> GSM907812 1 0 1 1 0
#> GSM907815 1 0 1 1 0
#> GSM907817 1 0 1 1 0
#> GSM907821 1 0 1 1 0
#> GSM907824 1 0 1 1 0
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907859 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907860 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907854 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907855 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907856 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907857 3 0.0747 0.965 0.000 0.016 0.984
#> GSM907825 3 0.1163 0.960 0.000 0.028 0.972
#> GSM907828 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907832 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907833 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907834 3 0.1163 0.960 0.000 0.028 0.972
#> GSM907826 2 0.6295 0.749 0.000 0.528 0.472
#> GSM907827 3 0.1163 0.960 0.000 0.028 0.972
#> GSM907829 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907830 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907831 3 0.1163 0.960 0.000 0.028 0.972
#> GSM907792 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907795 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907801 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907802 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907804 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907805 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907806 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907793 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907794 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907796 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907797 1 0.4931 0.877 0.768 0.232 0.000
#> GSM907798 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907799 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907800 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907803 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907864 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907865 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907868 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907869 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907870 2 0.6192 0.812 0.000 0.580 0.420
#> GSM907861 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907862 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907863 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907866 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907867 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907839 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907840 2 0.6295 0.749 0.000 0.528 0.472
#> GSM907842 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907843 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907845 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907846 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907848 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907851 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907835 2 0.6295 0.749 0.000 0.528 0.472
#> GSM907836 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907837 2 0.6308 0.711 0.000 0.508 0.492
#> GSM907838 2 0.6308 0.711 0.000 0.508 0.492
#> GSM907841 3 0.0000 0.988 0.000 0.000 1.000
#> GSM907844 2 0.6295 0.749 0.000 0.528 0.472
#> GSM907847 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907849 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907850 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907852 2 0.6295 0.749 0.000 0.528 0.472
#> GSM907853 2 0.5678 0.908 0.000 0.684 0.316
#> GSM907807 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907813 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907814 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907816 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907818 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907819 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907820 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907822 1 0.5397 0.884 0.720 0.280 0.000
#> GSM907823 1 0.5397 0.884 0.720 0.280 0.000
#> GSM907808 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907809 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907810 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907811 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907812 1 0.5560 0.884 0.700 0.300 0.000
#> GSM907815 1 0.1031 0.851 0.976 0.024 0.000
#> GSM907817 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907821 1 0.0000 0.856 1.000 0.000 0.000
#> GSM907824 2 0.6008 0.392 0.372 0.628 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907859 2 0.1022 0.770 0.000 0.968 0.000 0.032
#> GSM907860 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907854 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907855 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907856 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907857 3 0.3427 0.818 0.000 0.112 0.860 0.028
#> GSM907825 3 0.7392 0.552 0.000 0.172 0.472 0.356
#> GSM907828 2 0.3764 0.742 0.000 0.784 0.000 0.216
#> GSM907832 2 0.0592 0.778 0.000 0.984 0.000 0.016
#> GSM907833 2 0.3219 0.760 0.000 0.836 0.000 0.164
#> GSM907834 3 0.7332 0.566 0.000 0.164 0.480 0.356
#> GSM907826 2 0.6961 0.515 0.000 0.524 0.124 0.352
#> GSM907827 3 0.7332 0.566 0.000 0.164 0.480 0.356
#> GSM907829 2 0.0592 0.778 0.000 0.984 0.000 0.016
#> GSM907830 2 0.3400 0.756 0.000 0.820 0.000 0.180
#> GSM907831 3 0.7332 0.566 0.000 0.164 0.480 0.356
#> GSM907792 1 0.0000 0.949 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0469 0.949 0.988 0.000 0.012 0.000
#> GSM907801 1 0.0000 0.949 1.000 0.000 0.000 0.000
#> GSM907802 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907804 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907805 1 0.0188 0.949 0.996 0.000 0.004 0.000
#> GSM907806 4 0.6299 0.880 0.420 0.000 0.060 0.520
#> GSM907793 1 0.0921 0.941 0.972 0.000 0.028 0.000
#> GSM907794 4 0.6299 0.880 0.420 0.000 0.060 0.520
#> GSM907796 1 0.0817 0.942 0.976 0.000 0.024 0.000
#> GSM907797 1 0.5650 0.433 0.716 0.000 0.104 0.180
#> GSM907798 1 0.1022 0.941 0.968 0.000 0.032 0.000
#> GSM907799 1 0.0188 0.948 0.996 0.000 0.004 0.000
#> GSM907800 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907803 4 0.6305 0.876 0.424 0.000 0.060 0.516
#> GSM907864 2 0.0707 0.775 0.000 0.980 0.000 0.020
#> GSM907865 2 0.0707 0.775 0.000 0.980 0.000 0.020
#> GSM907868 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907869 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907870 2 0.6028 0.647 0.000 0.644 0.076 0.280
#> GSM907861 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907862 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907863 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907866 3 0.2973 0.861 0.000 0.144 0.856 0.000
#> GSM907867 3 0.3658 0.860 0.000 0.144 0.836 0.020
#> GSM907839 2 0.0000 0.780 0.000 1.000 0.000 0.000
#> GSM907840 2 0.6930 0.516 0.000 0.524 0.120 0.356
#> GSM907842 2 0.0000 0.780 0.000 1.000 0.000 0.000
#> GSM907843 2 0.0469 0.779 0.000 0.988 0.000 0.012
#> GSM907845 2 0.0592 0.778 0.000 0.984 0.000 0.016
#> GSM907846 2 0.1211 0.760 0.000 0.960 0.000 0.040
#> GSM907848 2 0.3266 0.759 0.000 0.832 0.000 0.168
#> GSM907851 2 0.0469 0.779 0.000 0.988 0.000 0.012
#> GSM907835 2 0.6961 0.515 0.000 0.524 0.124 0.352
#> GSM907836 2 0.4134 0.720 0.000 0.740 0.000 0.260
#> GSM907837 2 0.7042 0.499 0.000 0.516 0.132 0.352
#> GSM907838 2 0.7042 0.499 0.000 0.516 0.132 0.352
#> GSM907841 3 0.7191 0.591 0.000 0.148 0.500 0.352
#> GSM907844 2 0.6961 0.515 0.000 0.524 0.124 0.352
#> GSM907847 2 0.0469 0.779 0.000 0.988 0.000 0.012
#> GSM907849 2 0.0592 0.778 0.000 0.984 0.000 0.016
#> GSM907850 2 0.0921 0.781 0.000 0.972 0.000 0.028
#> GSM907852 2 0.6961 0.515 0.000 0.524 0.124 0.352
#> GSM907853 2 0.4134 0.720 0.000 0.740 0.000 0.260
#> GSM907807 1 0.0000 0.949 1.000 0.000 0.000 0.000
#> GSM907813 4 0.6299 0.880 0.420 0.000 0.060 0.520
#> GSM907814 1 0.0336 0.949 0.992 0.000 0.008 0.000
#> GSM907816 1 0.1118 0.923 0.964 0.000 0.036 0.000
#> GSM907818 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907819 4 0.5708 0.895 0.416 0.000 0.028 0.556
#> GSM907820 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907822 1 0.2222 0.879 0.924 0.000 0.060 0.016
#> GSM907823 1 0.2222 0.879 0.924 0.000 0.060 0.016
#> GSM907808 1 0.0469 0.949 0.988 0.000 0.012 0.000
#> GSM907809 1 0.0469 0.949 0.988 0.000 0.012 0.000
#> GSM907810 1 0.0336 0.949 0.992 0.000 0.008 0.000
#> GSM907811 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907812 1 0.0817 0.942 0.976 0.000 0.024 0.000
#> GSM907815 4 0.6851 0.779 0.400 0.000 0.104 0.496
#> GSM907817 4 0.4898 0.905 0.416 0.000 0.000 0.584
#> GSM907821 4 0.5320 0.902 0.416 0.000 0.012 0.572
#> GSM907824 4 0.6170 0.416 0.068 0.332 0.000 0.600
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907859 2 0.2920 0.727 0.000 0.852 0.000 0.016 0.132
#> GSM907860 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907854 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907855 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907856 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907857 3 0.3052 0.845 0.000 0.016 0.876 0.072 0.036
#> GSM907825 4 0.5879 0.674 0.000 0.052 0.300 0.608 0.040
#> GSM907828 2 0.4196 0.372 0.000 0.640 0.000 0.356 0.004
#> GSM907832 2 0.0963 0.755 0.000 0.964 0.000 0.000 0.036
#> GSM907833 2 0.3814 0.530 0.000 0.720 0.000 0.276 0.004
#> GSM907834 4 0.5930 0.663 0.000 0.052 0.312 0.596 0.040
#> GSM907826 4 0.5279 0.724 0.000 0.268 0.076 0.652 0.004
#> GSM907827 4 0.5945 0.657 0.000 0.052 0.316 0.592 0.040
#> GSM907829 2 0.2068 0.747 0.000 0.904 0.000 0.004 0.092
#> GSM907830 2 0.4009 0.466 0.000 0.684 0.000 0.312 0.004
#> GSM907831 4 0.5930 0.663 0.000 0.052 0.312 0.596 0.040
#> GSM907792 1 0.0000 0.929 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0566 0.928 0.984 0.000 0.004 0.012 0.000
#> GSM907801 1 0.0000 0.929 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907804 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907805 1 0.0290 0.929 0.992 0.000 0.000 0.008 0.000
#> GSM907806 5 0.5551 0.875 0.284 0.000 0.000 0.104 0.612
#> GSM907793 1 0.1544 0.908 0.932 0.000 0.000 0.068 0.000
#> GSM907794 5 0.5506 0.877 0.284 0.000 0.000 0.100 0.616
#> GSM907796 1 0.1478 0.909 0.936 0.000 0.000 0.064 0.000
#> GSM907797 1 0.6567 0.328 0.572 0.000 0.028 0.236 0.164
#> GSM907798 1 0.1638 0.908 0.932 0.000 0.004 0.064 0.000
#> GSM907799 1 0.0404 0.926 0.988 0.000 0.000 0.012 0.000
#> GSM907800 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907803 5 0.5570 0.872 0.288 0.000 0.000 0.104 0.608
#> GSM907864 2 0.2983 0.712 0.000 0.864 0.000 0.040 0.096
#> GSM907865 2 0.2983 0.712 0.000 0.864 0.000 0.040 0.096
#> GSM907868 3 0.2629 0.939 0.000 0.032 0.896 0.008 0.064
#> GSM907869 3 0.3272 0.923 0.000 0.032 0.856 0.012 0.100
#> GSM907870 2 0.6992 -0.219 0.000 0.428 0.056 0.412 0.104
#> GSM907861 3 0.3272 0.923 0.000 0.032 0.856 0.012 0.100
#> GSM907862 3 0.2694 0.938 0.000 0.032 0.892 0.008 0.068
#> GSM907863 3 0.2694 0.938 0.000 0.032 0.892 0.008 0.068
#> GSM907866 3 0.0880 0.944 0.000 0.032 0.968 0.000 0.000
#> GSM907867 3 0.3272 0.922 0.000 0.032 0.856 0.012 0.100
#> GSM907839 2 0.0955 0.750 0.000 0.968 0.000 0.028 0.004
#> GSM907840 4 0.5603 0.693 0.000 0.288 0.076 0.624 0.012
#> GSM907842 2 0.0794 0.750 0.000 0.972 0.000 0.028 0.000
#> GSM907843 2 0.1908 0.748 0.000 0.908 0.000 0.000 0.092
#> GSM907845 2 0.2068 0.747 0.000 0.904 0.000 0.004 0.092
#> GSM907846 2 0.2020 0.744 0.000 0.900 0.000 0.000 0.100
#> GSM907848 2 0.3838 0.524 0.000 0.716 0.000 0.280 0.004
#> GSM907851 2 0.1908 0.748 0.000 0.908 0.000 0.000 0.092
#> GSM907835 4 0.5279 0.724 0.000 0.268 0.076 0.652 0.004
#> GSM907836 2 0.4549 0.027 0.000 0.528 0.000 0.464 0.008
#> GSM907837 4 0.5483 0.736 0.000 0.256 0.088 0.648 0.008
#> GSM907838 4 0.5483 0.736 0.000 0.256 0.088 0.648 0.008
#> GSM907841 4 0.5732 0.630 0.000 0.036 0.328 0.596 0.040
#> GSM907844 4 0.5240 0.731 0.000 0.252 0.080 0.664 0.004
#> GSM907847 2 0.0404 0.755 0.000 0.988 0.000 0.000 0.012
#> GSM907849 2 0.2068 0.747 0.000 0.904 0.000 0.004 0.092
#> GSM907850 2 0.1544 0.737 0.000 0.932 0.000 0.068 0.000
#> GSM907852 4 0.5310 0.729 0.000 0.264 0.080 0.652 0.004
#> GSM907853 2 0.4268 0.126 0.000 0.556 0.000 0.444 0.000
#> GSM907807 1 0.0000 0.929 1.000 0.000 0.000 0.000 0.000
#> GSM907813 5 0.5551 0.875 0.284 0.000 0.000 0.104 0.612
#> GSM907814 1 0.0451 0.928 0.988 0.000 0.004 0.008 0.000
#> GSM907816 1 0.1671 0.881 0.924 0.000 0.000 0.076 0.000
#> GSM907818 5 0.3934 0.904 0.276 0.000 0.000 0.008 0.716
#> GSM907819 5 0.5117 0.891 0.276 0.000 0.000 0.072 0.652
#> GSM907820 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907822 1 0.2795 0.829 0.872 0.000 0.000 0.100 0.028
#> GSM907823 1 0.2795 0.829 0.872 0.000 0.000 0.100 0.028
#> GSM907808 1 0.0566 0.928 0.984 0.000 0.004 0.012 0.000
#> GSM907809 1 0.0566 0.928 0.984 0.000 0.004 0.012 0.000
#> GSM907810 1 0.0324 0.928 0.992 0.000 0.004 0.004 0.000
#> GSM907811 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907812 1 0.1410 0.910 0.940 0.000 0.000 0.060 0.000
#> GSM907815 5 0.7119 0.634 0.272 0.000 0.028 0.228 0.472
#> GSM907817 5 0.3661 0.905 0.276 0.000 0.000 0.000 0.724
#> GSM907821 5 0.4622 0.900 0.276 0.000 0.000 0.040 0.684
#> GSM907824 5 0.3667 0.596 0.020 0.156 0.000 0.012 0.812
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.1138 0.889 0.000 0.000 0.960 0.012 0.004 NA
#> GSM907859 4 0.2815 0.713 0.000 0.000 0.000 0.848 0.032 NA
#> GSM907860 3 0.0363 0.893 0.000 0.000 0.988 0.012 0.000 NA
#> GSM907854 3 0.0508 0.894 0.000 0.000 0.984 0.012 0.000 NA
#> GSM907855 3 0.1138 0.889 0.000 0.000 0.960 0.012 0.004 NA
#> GSM907856 3 0.1138 0.889 0.000 0.000 0.960 0.012 0.004 NA
#> GSM907857 3 0.2737 0.805 0.000 0.000 0.832 0.004 0.004 NA
#> GSM907825 2 0.5526 0.714 0.000 0.692 0.144 0.020 0.064 NA
#> GSM907828 4 0.5347 0.219 0.000 0.384 0.000 0.504 0.000 NA
#> GSM907832 4 0.0146 0.746 0.000 0.000 0.000 0.996 0.004 NA
#> GSM907833 4 0.5221 0.372 0.000 0.328 0.000 0.560 0.000 NA
#> GSM907834 2 0.5660 0.702 0.000 0.676 0.160 0.020 0.064 NA
#> GSM907826 2 0.2979 0.767 0.000 0.848 0.032 0.112 0.008 NA
#> GSM907827 2 0.5660 0.702 0.000 0.676 0.160 0.020 0.064 NA
#> GSM907829 4 0.1845 0.740 0.000 0.000 0.000 0.920 0.052 NA
#> GSM907830 4 0.5327 0.258 0.000 0.372 0.000 0.516 0.000 NA
#> GSM907831 2 0.5660 0.702 0.000 0.676 0.160 0.020 0.064 NA
#> GSM907792 1 0.0000 0.898 1.000 0.000 0.000 0.000 0.000 NA
#> GSM907795 1 0.1218 0.897 0.956 0.028 0.004 0.000 0.000 NA
#> GSM907801 1 0.0146 0.898 0.996 0.000 0.000 0.000 0.000 NA
#> GSM907802 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907804 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907805 1 0.0458 0.899 0.984 0.016 0.000 0.000 0.000 NA
#> GSM907806 5 0.5974 0.821 0.152 0.104 0.000 0.000 0.624 NA
#> GSM907793 1 0.2487 0.870 0.876 0.032 0.000 0.000 0.000 NA
#> GSM907794 5 0.5912 0.826 0.144 0.108 0.000 0.000 0.632 NA
#> GSM907796 1 0.2436 0.871 0.880 0.032 0.000 0.000 0.000 NA
#> GSM907797 1 0.5922 0.269 0.448 0.008 0.008 0.000 0.124 NA
#> GSM907798 1 0.2537 0.870 0.872 0.032 0.000 0.000 0.000 NA
#> GSM907799 1 0.0717 0.895 0.976 0.016 0.000 0.000 0.000 NA
#> GSM907800 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907803 5 0.6008 0.818 0.156 0.108 0.000 0.000 0.620 NA
#> GSM907864 4 0.4498 0.633 0.000 0.056 0.000 0.644 0.000 NA
#> GSM907865 4 0.4518 0.600 0.000 0.044 0.000 0.604 0.000 NA
#> GSM907868 3 0.3018 0.883 0.000 0.004 0.816 0.012 0.000 NA
#> GSM907869 3 0.3394 0.858 0.000 0.000 0.752 0.012 0.000 NA
#> GSM907870 2 0.6212 0.304 0.000 0.476 0.016 0.228 0.000 NA
#> GSM907861 3 0.3533 0.856 0.000 0.004 0.748 0.012 0.000 NA
#> GSM907862 3 0.3018 0.883 0.000 0.004 0.816 0.012 0.000 NA
#> GSM907863 3 0.3018 0.883 0.000 0.004 0.816 0.012 0.000 NA
#> GSM907866 3 0.0820 0.891 0.000 0.000 0.972 0.012 0.000 NA
#> GSM907867 3 0.3341 0.866 0.000 0.004 0.776 0.012 0.000 NA
#> GSM907839 4 0.3270 0.718 0.000 0.060 0.000 0.820 0.000 NA
#> GSM907840 2 0.4174 0.730 0.000 0.788 0.032 0.116 0.008 NA
#> GSM907842 4 0.3315 0.714 0.000 0.076 0.000 0.820 0.000 NA
#> GSM907843 4 0.1856 0.740 0.000 0.000 0.000 0.920 0.048 NA
#> GSM907845 4 0.1845 0.740 0.000 0.000 0.000 0.920 0.052 NA
#> GSM907846 4 0.1845 0.740 0.000 0.000 0.000 0.920 0.052 NA
#> GSM907848 4 0.5221 0.372 0.000 0.328 0.000 0.560 0.000 NA
#> GSM907851 4 0.1921 0.739 0.000 0.000 0.000 0.916 0.052 NA
#> GSM907835 2 0.2979 0.767 0.000 0.848 0.032 0.112 0.008 NA
#> GSM907836 2 0.5363 0.369 0.000 0.580 0.000 0.300 0.008 NA
#> GSM907837 2 0.3028 0.770 0.000 0.848 0.040 0.104 0.008 NA
#> GSM907838 2 0.3028 0.770 0.000 0.848 0.040 0.104 0.008 NA
#> GSM907841 2 0.5642 0.691 0.000 0.672 0.168 0.016 0.064 NA
#> GSM907844 2 0.3589 0.766 0.000 0.824 0.032 0.112 0.008 NA
#> GSM907847 4 0.1863 0.736 0.000 0.000 0.000 0.896 0.000 NA
#> GSM907849 4 0.1921 0.739 0.000 0.000 0.000 0.916 0.052 NA
#> GSM907850 4 0.3873 0.683 0.000 0.124 0.000 0.772 0.000 NA
#> GSM907852 2 0.2979 0.767 0.000 0.848 0.032 0.112 0.008 NA
#> GSM907853 2 0.5312 0.202 0.000 0.524 0.000 0.364 0.000 NA
#> GSM907807 1 0.0000 0.898 1.000 0.000 0.000 0.000 0.000 NA
#> GSM907813 5 0.5945 0.824 0.148 0.108 0.000 0.000 0.628 NA
#> GSM907814 1 0.0508 0.898 0.984 0.000 0.004 0.000 0.000 NA
#> GSM907816 1 0.2852 0.812 0.856 0.080 0.000 0.000 0.000 NA
#> GSM907818 5 0.2784 0.878 0.132 0.008 0.000 0.000 0.848 NA
#> GSM907819 5 0.5254 0.850 0.132 0.088 0.000 0.000 0.696 NA
#> GSM907820 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907822 1 0.4343 0.721 0.760 0.100 0.000 0.000 0.024 NA
#> GSM907823 1 0.4343 0.721 0.760 0.100 0.000 0.000 0.024 NA
#> GSM907808 1 0.1218 0.897 0.956 0.028 0.004 0.000 0.000 NA
#> GSM907809 1 0.1218 0.897 0.956 0.028 0.004 0.000 0.000 NA
#> GSM907810 1 0.0405 0.898 0.988 0.000 0.004 0.000 0.000 NA
#> GSM907811 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907812 1 0.2436 0.871 0.880 0.032 0.000 0.000 0.000 NA
#> GSM907815 5 0.6004 0.562 0.136 0.008 0.008 0.000 0.436 NA
#> GSM907817 5 0.2178 0.879 0.132 0.000 0.000 0.000 0.868 NA
#> GSM907821 5 0.4587 0.865 0.132 0.056 0.000 0.000 0.748 NA
#> GSM907824 5 0.1841 0.773 0.008 0.008 0.000 0.064 0.920 NA
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
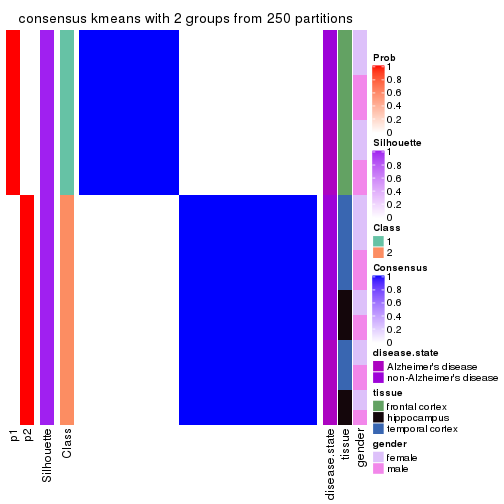
consensus_heatmap(res, k = 3)
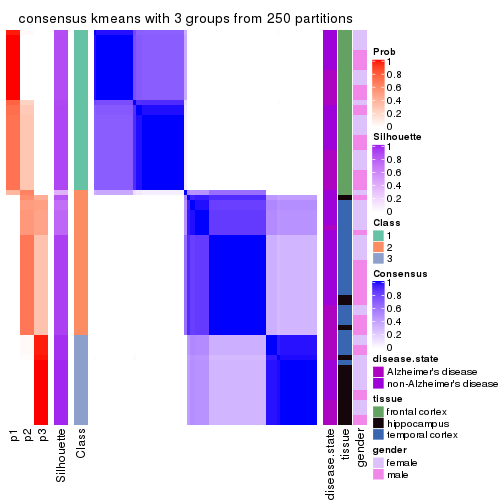
consensus_heatmap(res, k = 4)
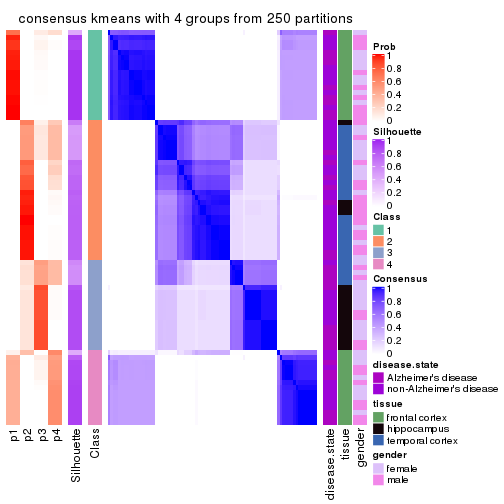
consensus_heatmap(res, k = 5)
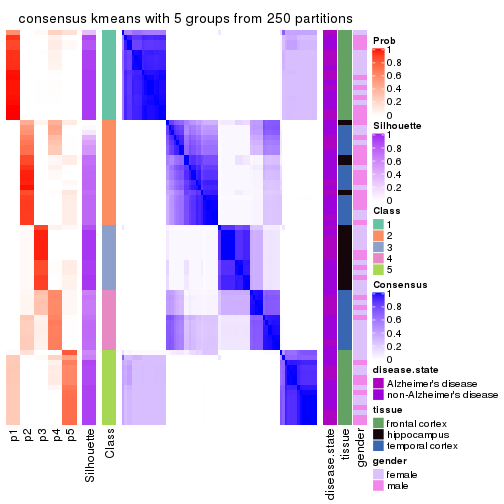
consensus_heatmap(res, k = 6)
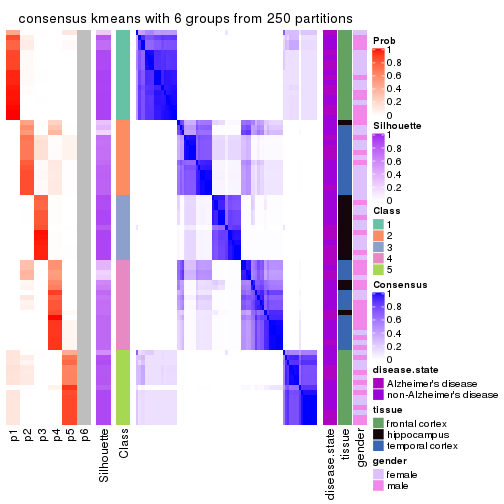
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
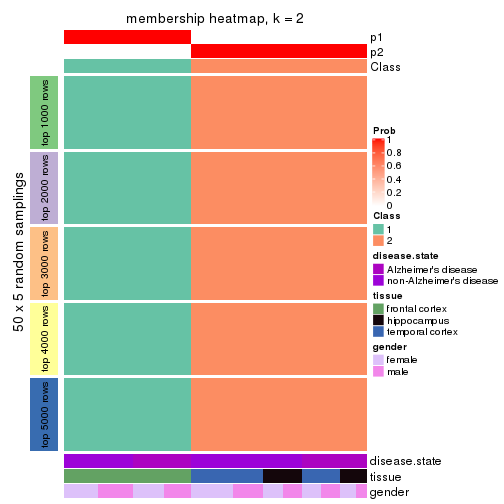
membership_heatmap(res, k = 3)
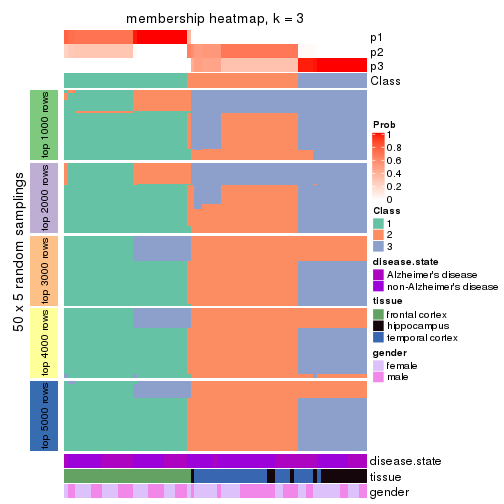
membership_heatmap(res, k = 4)
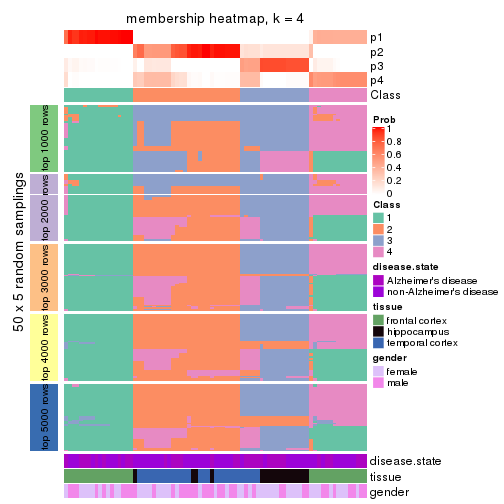
membership_heatmap(res, k = 5)
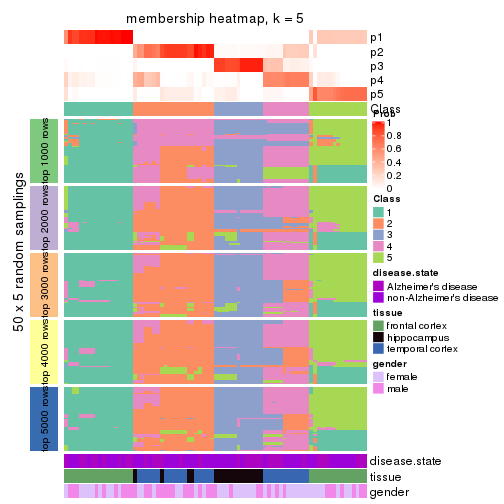
membership_heatmap(res, k = 6)
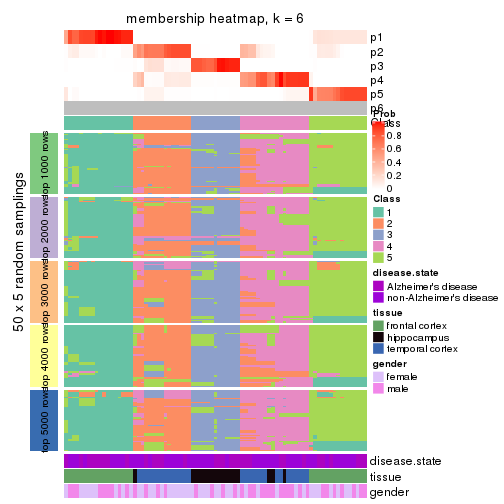
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
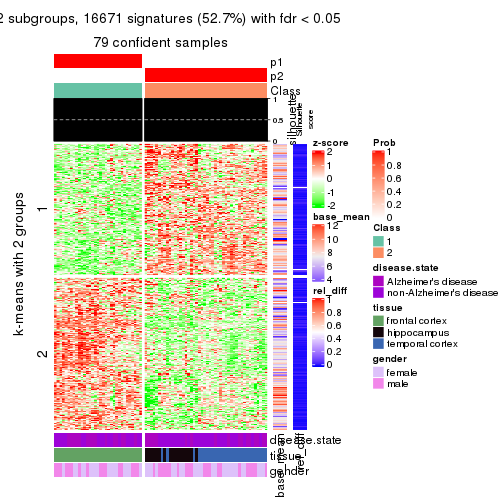
get_signatures(res, k = 3)
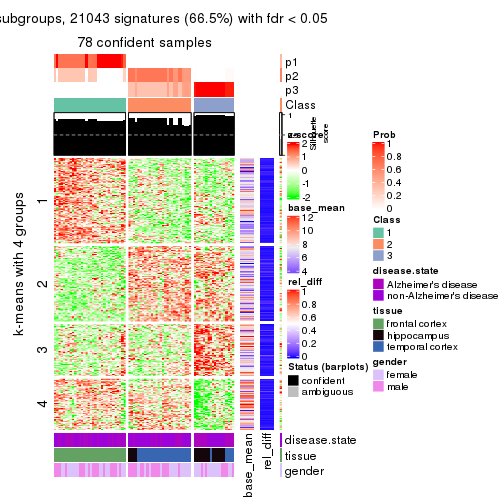
get_signatures(res, k = 4)
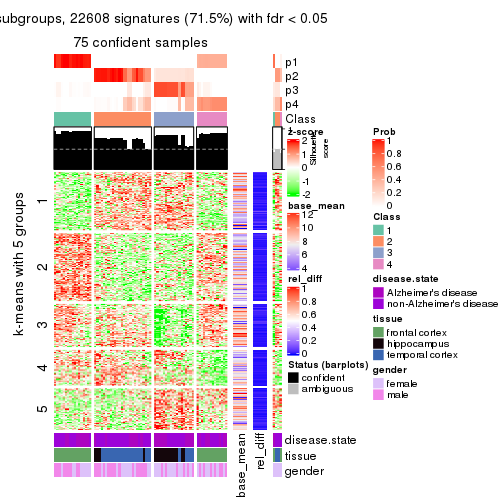
get_signatures(res, k = 5)
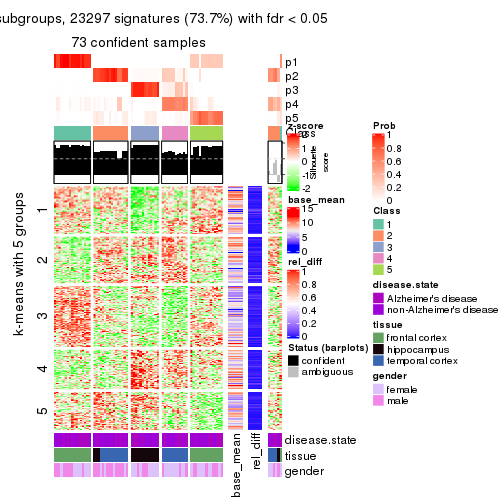
get_signatures(res, k = 6)
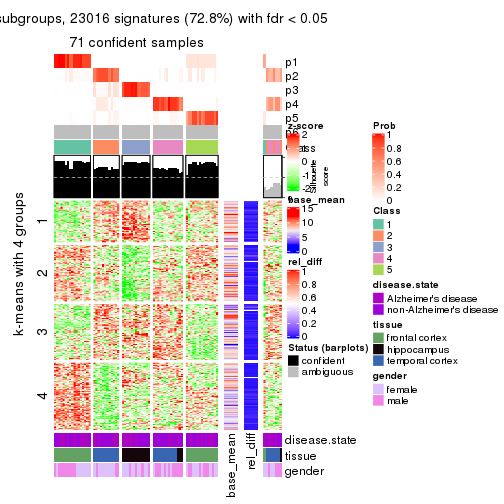
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
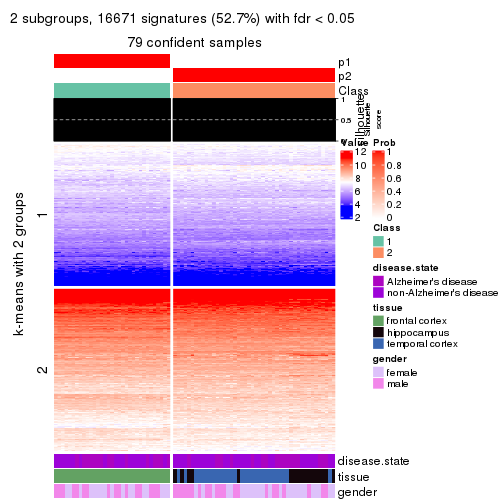
get_signatures(res, k = 3, scale_rows = FALSE)
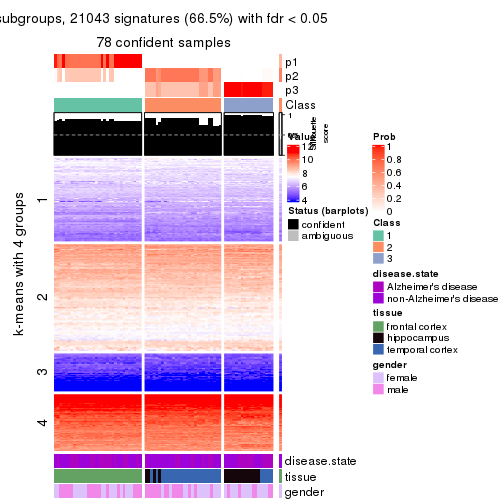
get_signatures(res, k = 4, scale_rows = FALSE)
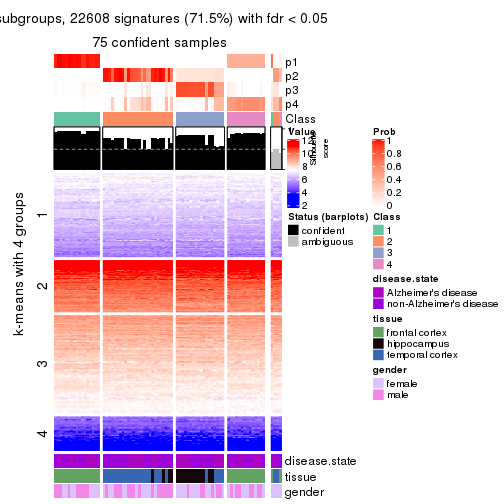
get_signatures(res, k = 5, scale_rows = FALSE)
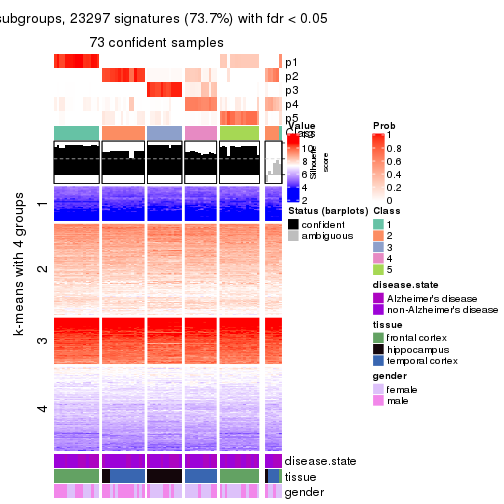
get_signatures(res, k = 6, scale_rows = FALSE)
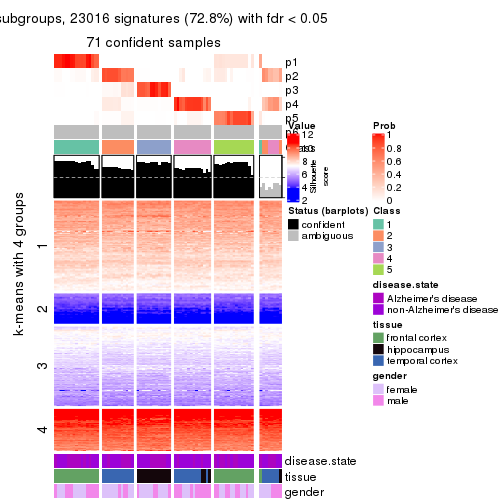
Compare the overlap of signatures from different k:
compare_signatures(res)
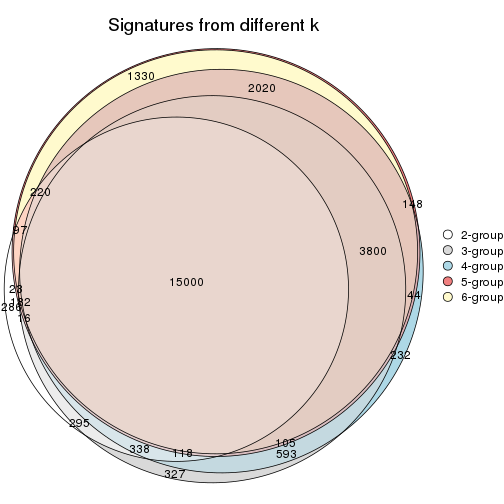
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
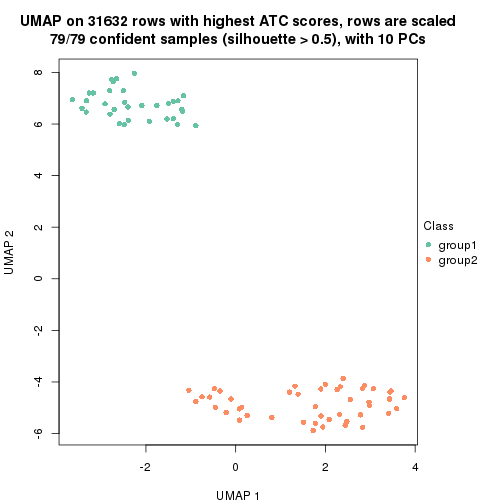
dimension_reduction(res, k = 3, method = "UMAP")
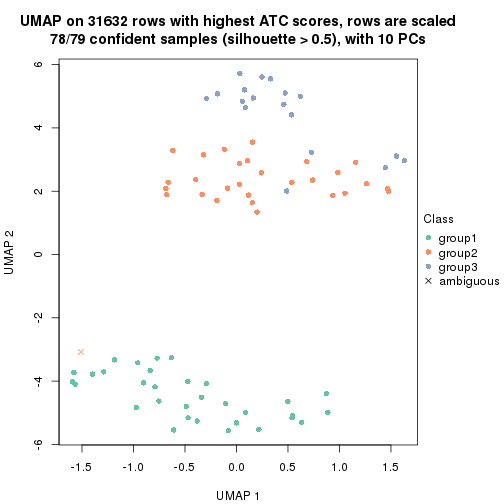
dimension_reduction(res, k = 4, method = "UMAP")
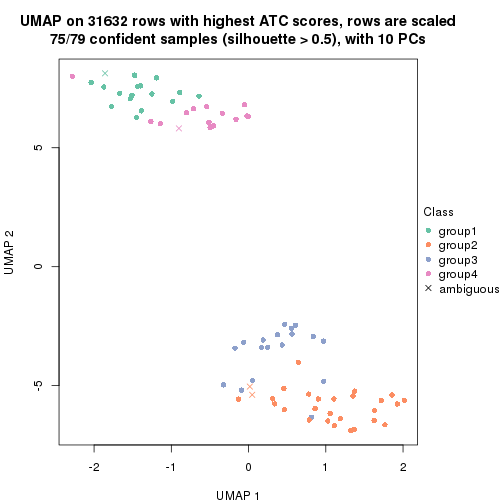
dimension_reduction(res, k = 5, method = "UMAP")
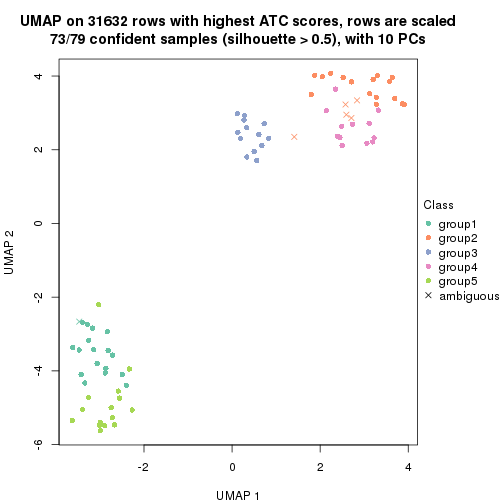
dimension_reduction(res, k = 6, method = "UMAP")
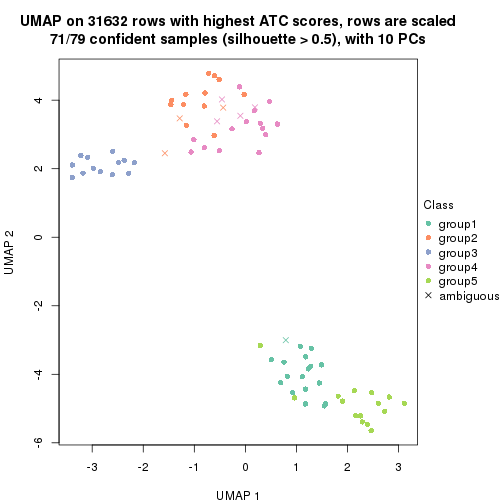
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
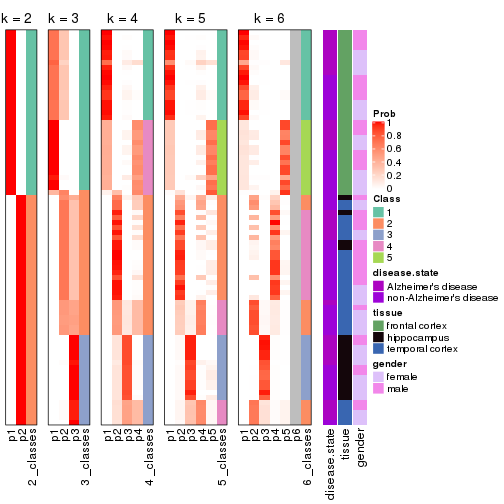
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:kmeans 79 0.5986 7.00e-18 0.9838 2
#> ATC:kmeans 78 0.0823 9.50e-22 0.3785 3
#> ATC:kmeans 75 0.2646 2.89e-19 0.4468 4
#> ATC:kmeans 73 0.7221 8.23e-24 0.0626 5
#> ATC:kmeans 71 0.6291 4.36e-23 0.1207 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "skmeans"]
# you can also extract it by
# res = res_list["ATC:skmeans"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 5.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
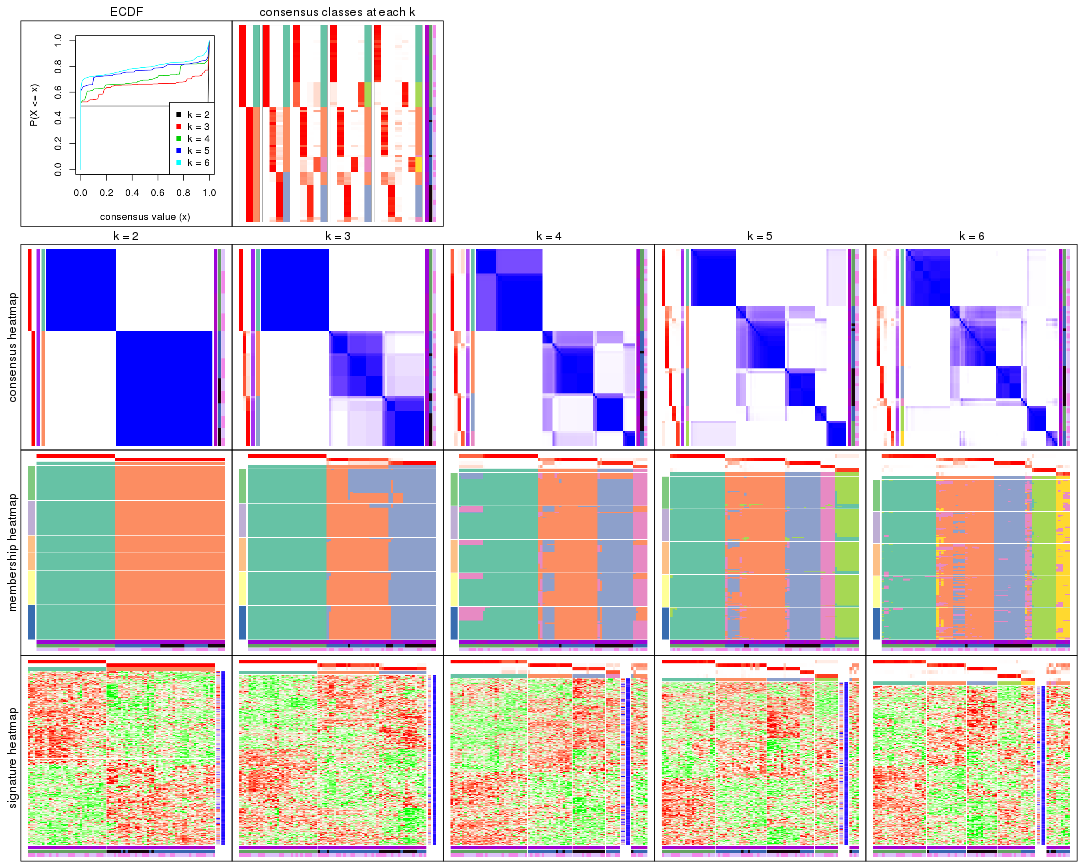
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
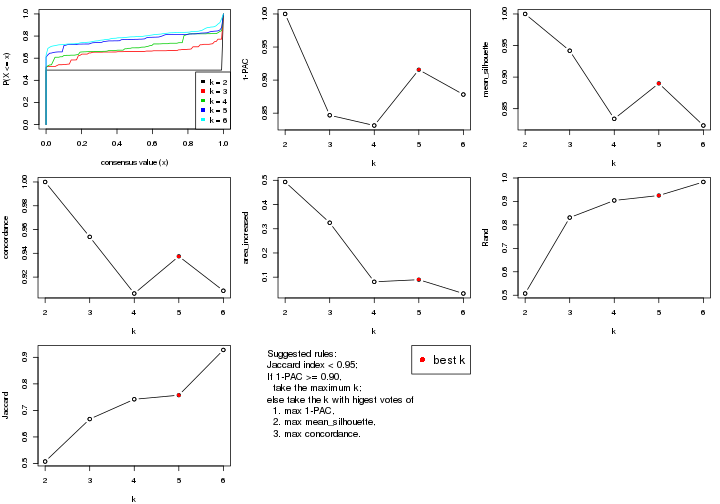
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 1.000 1.000 0.4932 0.507 0.507
#> 3 3 0.847 0.942 0.954 0.3248 0.831 0.667
#> 4 4 0.831 0.834 0.906 0.0809 0.904 0.742
#> 5 5 0.916 0.890 0.937 0.0896 0.925 0.757
#> 6 6 0.878 0.823 0.909 0.0325 0.983 0.928
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 5
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0 1 0 1
#> GSM907859 2 0 1 0 1
#> GSM907860 2 0 1 0 1
#> GSM907854 2 0 1 0 1
#> GSM907855 2 0 1 0 1
#> GSM907856 2 0 1 0 1
#> GSM907857 2 0 1 0 1
#> GSM907825 2 0 1 0 1
#> GSM907828 2 0 1 0 1
#> GSM907832 2 0 1 0 1
#> GSM907833 2 0 1 0 1
#> GSM907834 2 0 1 0 1
#> GSM907826 2 0 1 0 1
#> GSM907827 2 0 1 0 1
#> GSM907829 2 0 1 0 1
#> GSM907830 2 0 1 0 1
#> GSM907831 2 0 1 0 1
#> GSM907792 1 0 1 1 0
#> GSM907795 1 0 1 1 0
#> GSM907801 1 0 1 1 0
#> GSM907802 1 0 1 1 0
#> GSM907804 1 0 1 1 0
#> GSM907805 1 0 1 1 0
#> GSM907806 1 0 1 1 0
#> GSM907793 1 0 1 1 0
#> GSM907794 1 0 1 1 0
#> GSM907796 1 0 1 1 0
#> GSM907797 1 0 1 1 0
#> GSM907798 1 0 1 1 0
#> GSM907799 1 0 1 1 0
#> GSM907800 1 0 1 1 0
#> GSM907803 1 0 1 1 0
#> GSM907864 2 0 1 0 1
#> GSM907865 2 0 1 0 1
#> GSM907868 2 0 1 0 1
#> GSM907869 2 0 1 0 1
#> GSM907870 2 0 1 0 1
#> GSM907861 2 0 1 0 1
#> GSM907862 2 0 1 0 1
#> GSM907863 2 0 1 0 1
#> GSM907866 2 0 1 0 1
#> GSM907867 2 0 1 0 1
#> GSM907839 2 0 1 0 1
#> GSM907840 2 0 1 0 1
#> GSM907842 2 0 1 0 1
#> GSM907843 2 0 1 0 1
#> GSM907845 2 0 1 0 1
#> GSM907846 2 0 1 0 1
#> GSM907848 2 0 1 0 1
#> GSM907851 2 0 1 0 1
#> GSM907835 2 0 1 0 1
#> GSM907836 2 0 1 0 1
#> GSM907837 2 0 1 0 1
#> GSM907838 2 0 1 0 1
#> GSM907841 2 0 1 0 1
#> GSM907844 2 0 1 0 1
#> GSM907847 2 0 1 0 1
#> GSM907849 2 0 1 0 1
#> GSM907850 2 0 1 0 1
#> GSM907852 2 0 1 0 1
#> GSM907853 2 0 1 0 1
#> GSM907807 1 0 1 1 0
#> GSM907813 1 0 1 1 0
#> GSM907814 1 0 1 1 0
#> GSM907816 1 0 1 1 0
#> GSM907818 1 0 1 1 0
#> GSM907819 1 0 1 1 0
#> GSM907820 1 0 1 1 0
#> GSM907822 1 0 1 1 0
#> GSM907823 1 0 1 1 0
#> GSM907808 1 0 1 1 0
#> GSM907809 1 0 1 1 0
#> GSM907810 1 0 1 1 0
#> GSM907811 1 0 1 1 0
#> GSM907812 1 0 1 1 0
#> GSM907815 1 0 1 1 0
#> GSM907817 1 0 1 1 0
#> GSM907821 1 0 1 1 0
#> GSM907824 1 0 1 1 0
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.0000 0.961 0 0.000 1.000
#> GSM907859 3 0.3192 0.856 0 0.112 0.888
#> GSM907860 3 0.0000 0.961 0 0.000 1.000
#> GSM907854 3 0.0000 0.961 0 0.000 1.000
#> GSM907855 3 0.0000 0.961 0 0.000 1.000
#> GSM907856 3 0.0000 0.961 0 0.000 1.000
#> GSM907857 3 0.0000 0.961 0 0.000 1.000
#> GSM907825 3 0.2066 0.920 0 0.060 0.940
#> GSM907828 2 0.3686 0.913 0 0.860 0.140
#> GSM907832 2 0.0000 0.862 0 1.000 0.000
#> GSM907833 2 0.3686 0.913 0 0.860 0.140
#> GSM907834 3 0.2066 0.920 0 0.060 0.940
#> GSM907826 2 0.4235 0.902 0 0.824 0.176
#> GSM907827 3 0.2066 0.920 0 0.060 0.940
#> GSM907829 2 0.5216 0.561 0 0.740 0.260
#> GSM907830 2 0.3686 0.913 0 0.860 0.140
#> GSM907831 3 0.2066 0.920 0 0.060 0.940
#> GSM907792 1 0.0000 1.000 1 0.000 0.000
#> GSM907795 1 0.0000 1.000 1 0.000 0.000
#> GSM907801 1 0.0000 1.000 1 0.000 0.000
#> GSM907802 1 0.0000 1.000 1 0.000 0.000
#> GSM907804 1 0.0000 1.000 1 0.000 0.000
#> GSM907805 1 0.0000 1.000 1 0.000 0.000
#> GSM907806 1 0.0000 1.000 1 0.000 0.000
#> GSM907793 1 0.0000 1.000 1 0.000 0.000
#> GSM907794 1 0.0000 1.000 1 0.000 0.000
#> GSM907796 1 0.0000 1.000 1 0.000 0.000
#> GSM907797 1 0.0000 1.000 1 0.000 0.000
#> GSM907798 1 0.0000 1.000 1 0.000 0.000
#> GSM907799 1 0.0000 1.000 1 0.000 0.000
#> GSM907800 1 0.0000 1.000 1 0.000 0.000
#> GSM907803 1 0.0000 1.000 1 0.000 0.000
#> GSM907864 2 0.4346 0.889 0 0.816 0.184
#> GSM907865 3 0.5216 0.566 0 0.260 0.740
#> GSM907868 3 0.0000 0.961 0 0.000 1.000
#> GSM907869 3 0.0000 0.961 0 0.000 1.000
#> GSM907870 2 0.4235 0.902 0 0.824 0.176
#> GSM907861 3 0.0000 0.961 0 0.000 1.000
#> GSM907862 3 0.0000 0.961 0 0.000 1.000
#> GSM907863 3 0.0000 0.961 0 0.000 1.000
#> GSM907866 3 0.0000 0.961 0 0.000 1.000
#> GSM907867 3 0.0000 0.961 0 0.000 1.000
#> GSM907839 2 0.0237 0.864 0 0.996 0.004
#> GSM907840 2 0.4235 0.902 0 0.824 0.176
#> GSM907842 2 0.3619 0.913 0 0.864 0.136
#> GSM907843 2 0.0000 0.862 0 1.000 0.000
#> GSM907845 2 0.2165 0.833 0 0.936 0.064
#> GSM907846 2 0.0000 0.862 0 1.000 0.000
#> GSM907848 2 0.3686 0.913 0 0.860 0.140
#> GSM907851 2 0.0000 0.862 0 1.000 0.000
#> GSM907835 2 0.4235 0.902 0 0.824 0.176
#> GSM907836 2 0.3686 0.913 0 0.860 0.140
#> GSM907837 2 0.4235 0.902 0 0.824 0.176
#> GSM907838 2 0.4235 0.902 0 0.824 0.176
#> GSM907841 3 0.0000 0.961 0 0.000 1.000
#> GSM907844 2 0.4235 0.902 0 0.824 0.176
#> GSM907847 2 0.0000 0.862 0 1.000 0.000
#> GSM907849 2 0.0000 0.862 0 1.000 0.000
#> GSM907850 2 0.3686 0.913 0 0.860 0.140
#> GSM907852 2 0.4235 0.902 0 0.824 0.176
#> GSM907853 2 0.3686 0.913 0 0.860 0.140
#> GSM907807 1 0.0000 1.000 1 0.000 0.000
#> GSM907813 1 0.0000 1.000 1 0.000 0.000
#> GSM907814 1 0.0000 1.000 1 0.000 0.000
#> GSM907816 1 0.0000 1.000 1 0.000 0.000
#> GSM907818 1 0.0000 1.000 1 0.000 0.000
#> GSM907819 1 0.0000 1.000 1 0.000 0.000
#> GSM907820 1 0.0000 1.000 1 0.000 0.000
#> GSM907822 1 0.0000 1.000 1 0.000 0.000
#> GSM907823 1 0.0000 1.000 1 0.000 0.000
#> GSM907808 1 0.0000 1.000 1 0.000 0.000
#> GSM907809 1 0.0000 1.000 1 0.000 0.000
#> GSM907810 1 0.0000 1.000 1 0.000 0.000
#> GSM907811 1 0.0000 1.000 1 0.000 0.000
#> GSM907812 1 0.0000 1.000 1 0.000 0.000
#> GSM907815 1 0.0000 1.000 1 0.000 0.000
#> GSM907817 1 0.0000 1.000 1 0.000 0.000
#> GSM907821 1 0.0000 1.000 1 0.000 0.000
#> GSM907824 1 0.0000 1.000 1 0.000 0.000
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907859 3 0.4391 0.607 0.000 0.008 0.740 0.252
#> GSM907860 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907854 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907855 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907856 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907857 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907825 2 0.4855 0.388 0.000 0.600 0.400 0.000
#> GSM907828 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907832 2 0.4985 -0.203 0.000 0.532 0.000 0.468
#> GSM907833 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907834 2 0.4855 0.388 0.000 0.600 0.400 0.000
#> GSM907826 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907827 2 0.4941 0.301 0.000 0.564 0.436 0.000
#> GSM907829 4 0.4426 0.852 0.000 0.096 0.092 0.812
#> GSM907830 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907831 2 0.4866 0.379 0.000 0.596 0.404 0.000
#> GSM907792 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907802 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907804 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907805 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907806 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907793 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907794 1 0.0921 0.922 0.972 0.000 0.000 0.028
#> GSM907796 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907797 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907798 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907799 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907800 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907803 1 0.0188 0.931 0.996 0.000 0.000 0.004
#> GSM907864 2 0.1022 0.812 0.000 0.968 0.032 0.000
#> GSM907865 3 0.4661 0.467 0.000 0.348 0.652 0.000
#> GSM907868 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907869 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907870 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907861 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907862 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907863 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907866 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907867 3 0.1211 0.949 0.000 0.040 0.960 0.000
#> GSM907839 2 0.1118 0.791 0.000 0.964 0.000 0.036
#> GSM907840 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907842 2 0.0336 0.825 0.000 0.992 0.000 0.008
#> GSM907843 4 0.3486 0.964 0.000 0.188 0.000 0.812
#> GSM907845 4 0.3881 0.953 0.000 0.172 0.016 0.812
#> GSM907846 4 0.3486 0.964 0.000 0.188 0.000 0.812
#> GSM907848 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907851 4 0.3486 0.964 0.000 0.188 0.000 0.812
#> GSM907835 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907836 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907837 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907838 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907841 2 0.4916 0.331 0.000 0.576 0.424 0.000
#> GSM907844 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907847 2 0.3764 0.537 0.000 0.784 0.000 0.216
#> GSM907849 4 0.3486 0.964 0.000 0.188 0.000 0.812
#> GSM907850 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0188 0.834 0.000 0.996 0.004 0.000
#> GSM907853 2 0.0000 0.833 0.000 1.000 0.000 0.000
#> GSM907807 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907813 1 0.0188 0.931 0.996 0.000 0.000 0.004
#> GSM907814 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907816 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907818 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907819 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907820 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907822 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907811 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907812 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907815 1 0.0000 0.932 1.000 0.000 0.000 0.000
#> GSM907817 1 0.4636 0.833 0.772 0.000 0.040 0.188
#> GSM907821 1 0.4323 0.840 0.788 0.000 0.028 0.184
#> GSM907824 1 0.4636 0.833 0.772 0.000 0.040 0.188
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907859 3 0.4946 0.466 0.000 0.000 0.648 0.300 0.052
#> GSM907860 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907854 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907855 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0162 0.940 0.000 0.000 0.996 0.000 0.004
#> GSM907825 2 0.4317 0.573 0.000 0.668 0.320 0.008 0.004
#> GSM907828 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907832 2 0.4696 0.276 0.000 0.556 0.000 0.428 0.016
#> GSM907833 2 0.0290 0.868 0.000 0.992 0.000 0.000 0.008
#> GSM907834 2 0.4335 0.567 0.000 0.664 0.324 0.008 0.004
#> GSM907826 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907827 2 0.4645 0.380 0.000 0.564 0.424 0.008 0.004
#> GSM907829 4 0.0955 0.975 0.000 0.004 0.000 0.968 0.028
#> GSM907830 2 0.0162 0.869 0.000 0.996 0.000 0.000 0.004
#> GSM907831 2 0.4419 0.536 0.000 0.644 0.344 0.008 0.004
#> GSM907792 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907804 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907805 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907806 1 0.0162 0.991 0.996 0.000 0.000 0.000 0.004
#> GSM907793 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907794 1 0.1792 0.900 0.916 0.000 0.000 0.000 0.084
#> GSM907796 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907797 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907798 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907799 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907800 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907803 1 0.0609 0.976 0.980 0.000 0.000 0.000 0.020
#> GSM907864 2 0.3297 0.799 0.000 0.868 0.040 0.032 0.060
#> GSM907865 3 0.5434 0.518 0.000 0.256 0.664 0.028 0.052
#> GSM907868 3 0.0290 0.941 0.000 0.000 0.992 0.000 0.008
#> GSM907869 3 0.0162 0.941 0.000 0.000 0.996 0.000 0.004
#> GSM907870 2 0.0771 0.862 0.000 0.976 0.004 0.000 0.020
#> GSM907861 3 0.0290 0.941 0.000 0.000 0.992 0.000 0.008
#> GSM907862 3 0.0290 0.941 0.000 0.000 0.992 0.000 0.008
#> GSM907863 3 0.0290 0.941 0.000 0.000 0.992 0.000 0.008
#> GSM907866 3 0.0000 0.942 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.0290 0.941 0.000 0.000 0.992 0.000 0.008
#> GSM907839 2 0.1918 0.838 0.000 0.928 0.000 0.036 0.036
#> GSM907840 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907842 2 0.0912 0.860 0.000 0.972 0.000 0.016 0.012
#> GSM907843 4 0.0912 0.972 0.000 0.012 0.000 0.972 0.016
#> GSM907845 4 0.0794 0.976 0.000 0.000 0.000 0.972 0.028
#> GSM907846 4 0.0992 0.979 0.000 0.008 0.000 0.968 0.024
#> GSM907848 2 0.0290 0.868 0.000 0.992 0.000 0.000 0.008
#> GSM907851 4 0.0693 0.976 0.000 0.012 0.000 0.980 0.008
#> GSM907835 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.0162 0.869 0.000 0.996 0.000 0.000 0.004
#> GSM907837 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907841 2 0.4524 0.390 0.000 0.572 0.420 0.004 0.004
#> GSM907844 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907847 2 0.3476 0.718 0.000 0.804 0.000 0.176 0.020
#> GSM907849 4 0.0290 0.980 0.000 0.008 0.000 0.992 0.000
#> GSM907850 2 0.0693 0.864 0.000 0.980 0.000 0.008 0.012
#> GSM907852 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.0000 0.869 0.000 1.000 0.000 0.000 0.000
#> GSM907807 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.0510 0.980 0.984 0.000 0.000 0.000 0.016
#> GSM907814 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907818 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907819 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907820 5 0.1908 0.971 0.092 0.000 0.000 0.000 0.908
#> GSM907822 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907823 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907808 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907811 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907812 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907815 1 0.0000 0.994 1.000 0.000 0.000 0.000 0.000
#> GSM907817 5 0.1965 0.975 0.096 0.000 0.000 0.000 0.904
#> GSM907821 5 0.3452 0.780 0.244 0.000 0.000 0.000 0.756
#> GSM907824 5 0.1908 0.971 0.092 0.000 0.000 0.000 0.908
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907859 4 0.4704 0.4703 0.000 0.000 0.300 0.628 0.000 0.072
#> GSM907860 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907854 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907855 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907856 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907857 3 0.1007 0.9337 0.000 0.000 0.956 0.044 0.000 0.000
#> GSM907825 2 0.4249 0.5065 0.000 0.688 0.260 0.052 0.000 0.000
#> GSM907828 2 0.0547 0.7741 0.000 0.980 0.000 0.020 0.000 0.000
#> GSM907832 2 0.5842 0.0932 0.000 0.448 0.000 0.196 0.000 0.356
#> GSM907833 2 0.2006 0.7380 0.000 0.892 0.000 0.104 0.000 0.004
#> GSM907834 2 0.4352 0.4799 0.000 0.668 0.280 0.052 0.000 0.000
#> GSM907826 2 0.0000 0.7769 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907827 2 0.4736 0.2764 0.000 0.552 0.396 0.052 0.000 0.000
#> GSM907829 6 0.2020 0.8000 0.000 0.000 0.000 0.096 0.008 0.896
#> GSM907830 2 0.0363 0.7763 0.000 0.988 0.000 0.012 0.000 0.000
#> GSM907831 2 0.4426 0.4564 0.000 0.652 0.296 0.052 0.000 0.000
#> GSM907792 1 0.0000 0.9777 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907795 1 0.0146 0.9777 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907801 1 0.0000 0.9777 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907804 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907805 1 0.0146 0.9777 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907806 1 0.0363 0.9746 0.988 0.000 0.000 0.012 0.000 0.000
#> GSM907793 1 0.0458 0.9744 0.984 0.000 0.000 0.016 0.000 0.000
#> GSM907794 1 0.2070 0.8838 0.892 0.000 0.000 0.008 0.100 0.000
#> GSM907796 1 0.0458 0.9744 0.984 0.000 0.000 0.016 0.000 0.000
#> GSM907797 1 0.2053 0.9023 0.888 0.000 0.000 0.108 0.000 0.004
#> GSM907798 1 0.0458 0.9744 0.984 0.000 0.000 0.016 0.000 0.000
#> GSM907799 1 0.0146 0.9777 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907800 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907803 1 0.0806 0.9642 0.972 0.000 0.000 0.008 0.020 0.000
#> GSM907864 4 0.4411 0.1908 0.000 0.356 0.028 0.612 0.000 0.004
#> GSM907865 4 0.4828 0.5138 0.000 0.064 0.368 0.568 0.000 0.000
#> GSM907868 3 0.0713 0.9694 0.000 0.000 0.972 0.028 0.000 0.000
#> GSM907869 3 0.0632 0.9706 0.000 0.000 0.976 0.024 0.000 0.000
#> GSM907870 2 0.2003 0.7279 0.000 0.884 0.000 0.116 0.000 0.000
#> GSM907861 3 0.1007 0.9592 0.000 0.000 0.956 0.044 0.000 0.000
#> GSM907862 3 0.0865 0.9659 0.000 0.000 0.964 0.036 0.000 0.000
#> GSM907863 3 0.0865 0.9659 0.000 0.000 0.964 0.036 0.000 0.000
#> GSM907866 3 0.0000 0.9722 0.000 0.000 1.000 0.000 0.000 0.000
#> GSM907867 3 0.0865 0.9659 0.000 0.000 0.964 0.036 0.000 0.000
#> GSM907839 2 0.4458 0.3265 0.000 0.608 0.000 0.352 0.000 0.040
#> GSM907840 2 0.0547 0.7743 0.000 0.980 0.000 0.020 0.000 0.000
#> GSM907842 2 0.3003 0.6703 0.000 0.812 0.000 0.172 0.000 0.016
#> GSM907843 6 0.3390 0.7463 0.000 0.000 0.000 0.296 0.000 0.704
#> GSM907845 6 0.1531 0.8148 0.000 0.000 0.000 0.068 0.004 0.928
#> GSM907846 6 0.1124 0.8237 0.000 0.000 0.000 0.036 0.008 0.956
#> GSM907848 2 0.1908 0.7431 0.000 0.900 0.000 0.096 0.000 0.004
#> GSM907851 6 0.3151 0.7862 0.000 0.000 0.000 0.252 0.000 0.748
#> GSM907835 2 0.0000 0.7769 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907836 2 0.0937 0.7689 0.000 0.960 0.000 0.040 0.000 0.000
#> GSM907837 2 0.0000 0.7769 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.7769 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907841 2 0.4587 0.3578 0.000 0.596 0.356 0.048 0.000 0.000
#> GSM907844 2 0.0865 0.7643 0.000 0.964 0.000 0.036 0.000 0.000
#> GSM907847 2 0.5374 0.3275 0.000 0.580 0.000 0.252 0.000 0.168
#> GSM907849 6 0.2562 0.8195 0.000 0.000 0.000 0.172 0.000 0.828
#> GSM907850 2 0.2389 0.7173 0.000 0.864 0.000 0.128 0.000 0.008
#> GSM907852 2 0.0000 0.7769 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907853 2 0.0146 0.7768 0.000 0.996 0.000 0.004 0.000 0.000
#> GSM907807 1 0.0000 0.9777 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 1 0.1151 0.9526 0.956 0.000 0.000 0.012 0.032 0.000
#> GSM907814 1 0.0000 0.9777 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0146 0.9769 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907818 5 0.0405 0.9646 0.008 0.000 0.000 0.004 0.988 0.000
#> GSM907819 5 0.0717 0.9555 0.016 0.000 0.000 0.008 0.976 0.000
#> GSM907820 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907822 1 0.0363 0.9746 0.988 0.000 0.000 0.012 0.000 0.000
#> GSM907823 1 0.0363 0.9746 0.988 0.000 0.000 0.012 0.000 0.000
#> GSM907808 1 0.0146 0.9777 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907809 1 0.0146 0.9777 0.996 0.000 0.000 0.004 0.000 0.000
#> GSM907810 1 0.0000 0.9777 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907811 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907812 1 0.0458 0.9744 0.984 0.000 0.000 0.016 0.000 0.000
#> GSM907815 1 0.2053 0.9023 0.888 0.000 0.000 0.108 0.000 0.004
#> GSM907817 5 0.0260 0.9665 0.008 0.000 0.000 0.000 0.992 0.000
#> GSM907821 5 0.3014 0.7065 0.184 0.000 0.000 0.012 0.804 0.000
#> GSM907824 5 0.0405 0.9645 0.008 0.000 0.000 0.004 0.988 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
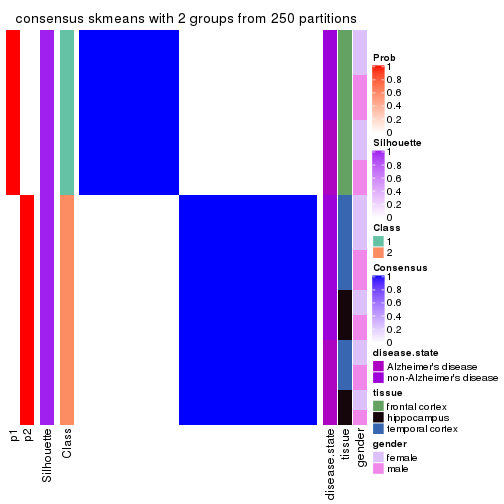
consensus_heatmap(res, k = 3)
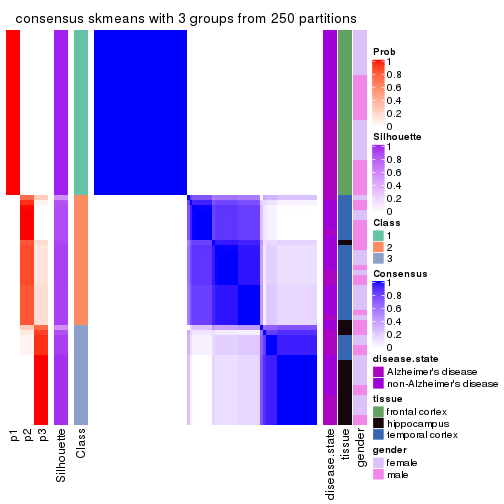
consensus_heatmap(res, k = 4)
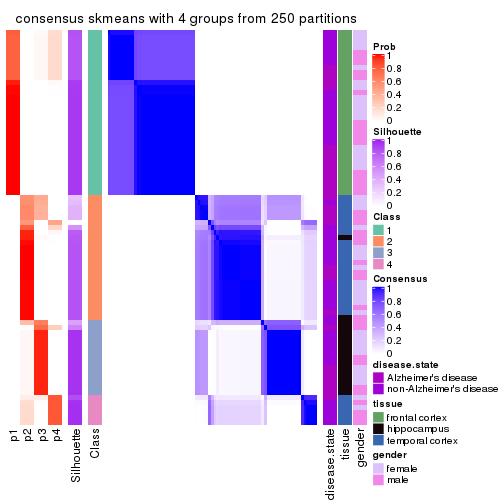
consensus_heatmap(res, k = 5)
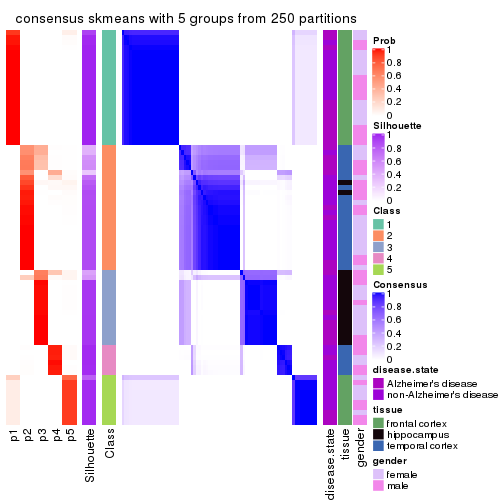
consensus_heatmap(res, k = 6)
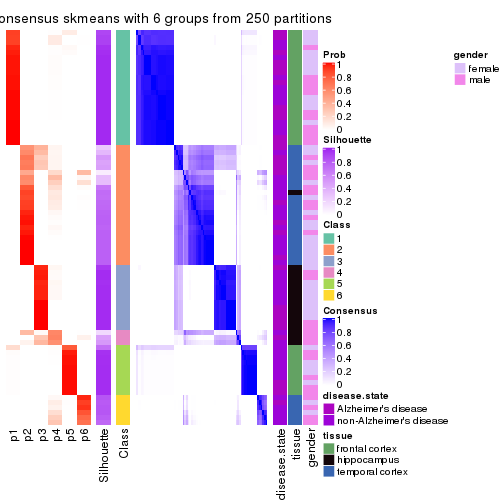
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
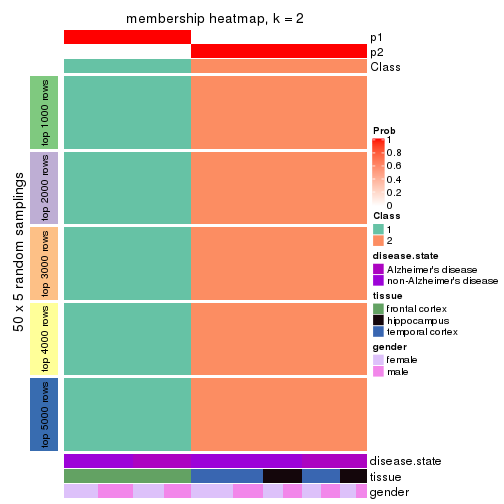
membership_heatmap(res, k = 3)
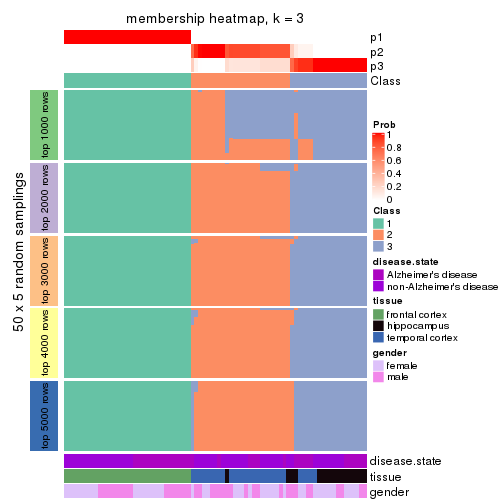
membership_heatmap(res, k = 4)
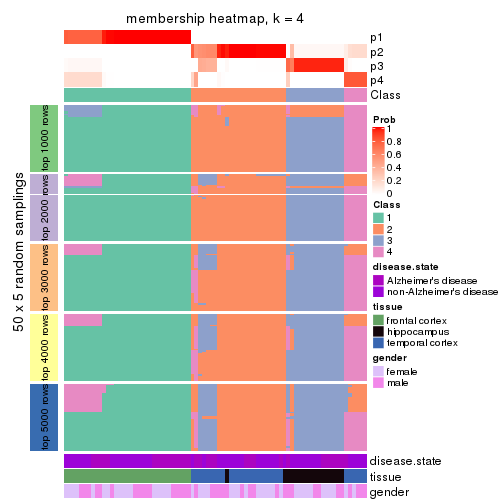
membership_heatmap(res, k = 5)
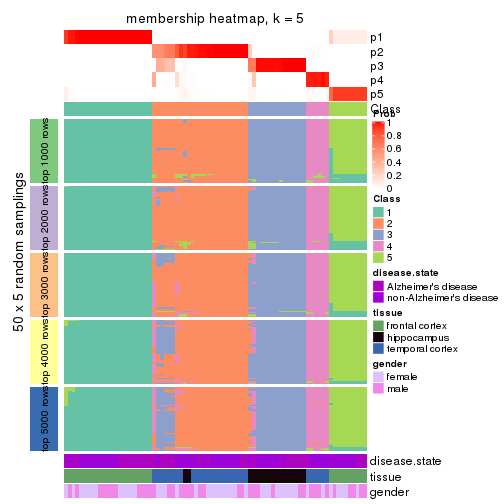
membership_heatmap(res, k = 6)
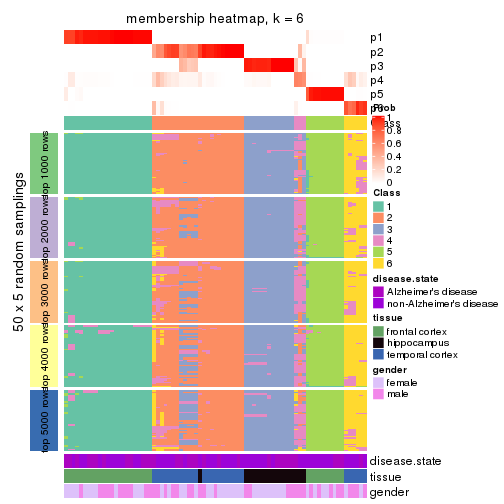
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
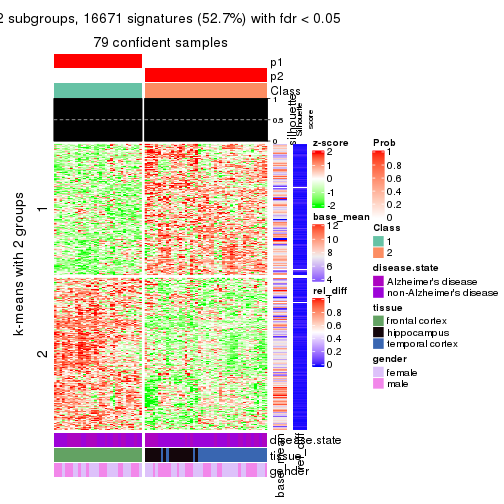
get_signatures(res, k = 3)
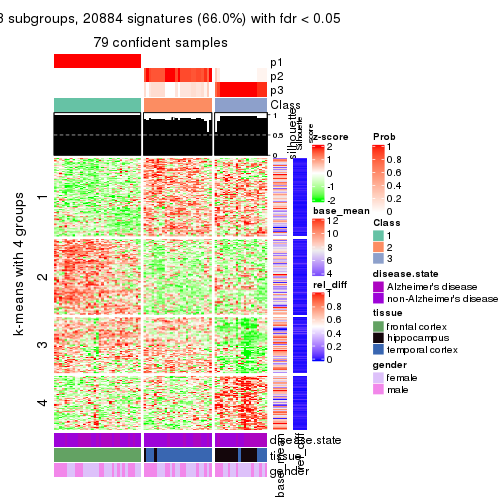
get_signatures(res, k = 4)
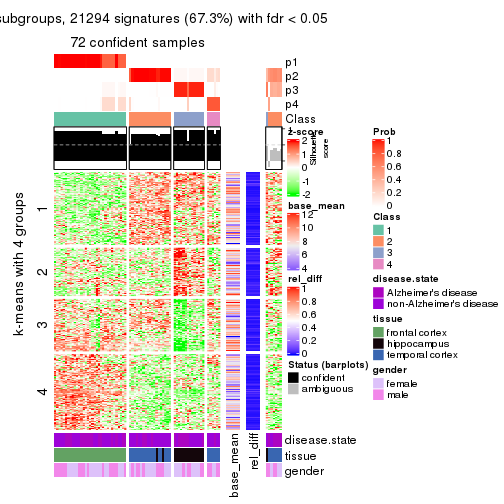
get_signatures(res, k = 5)
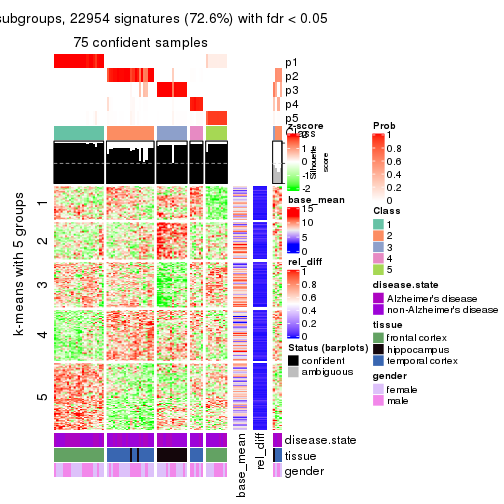
get_signatures(res, k = 6)
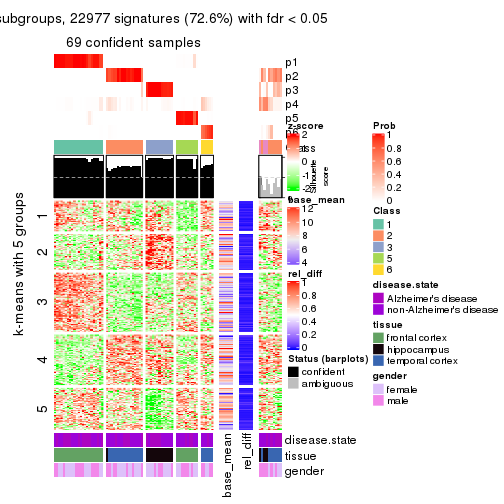
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
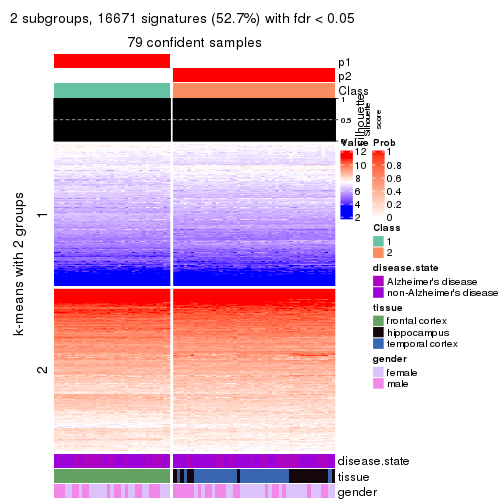
get_signatures(res, k = 3, scale_rows = FALSE)
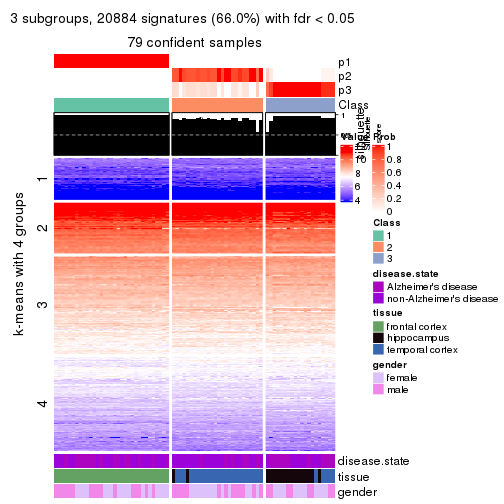
get_signatures(res, k = 4, scale_rows = FALSE)
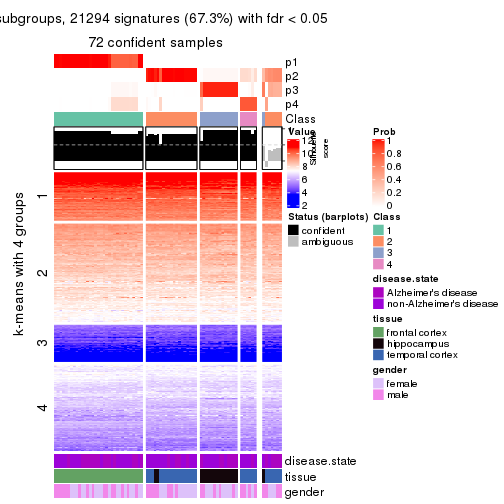
get_signatures(res, k = 5, scale_rows = FALSE)
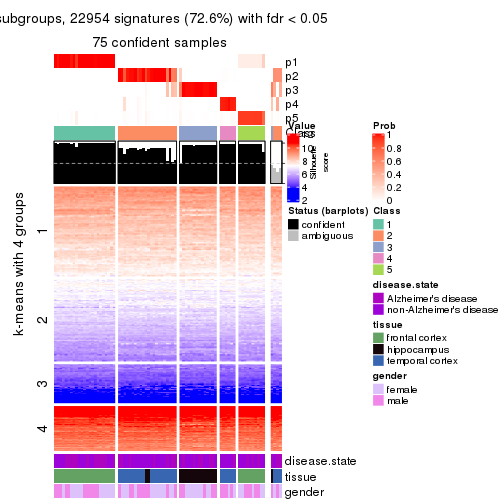
get_signatures(res, k = 6, scale_rows = FALSE)
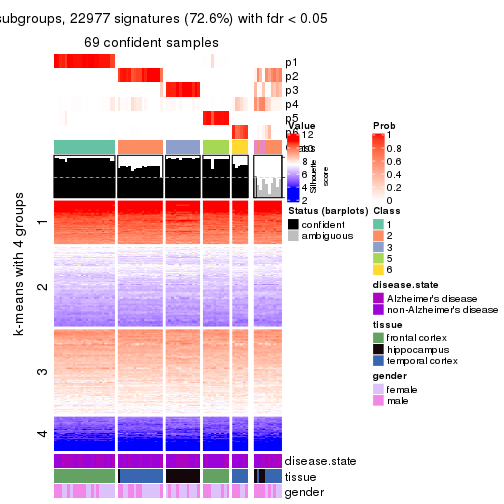
Compare the overlap of signatures from different k:
compare_signatures(res)
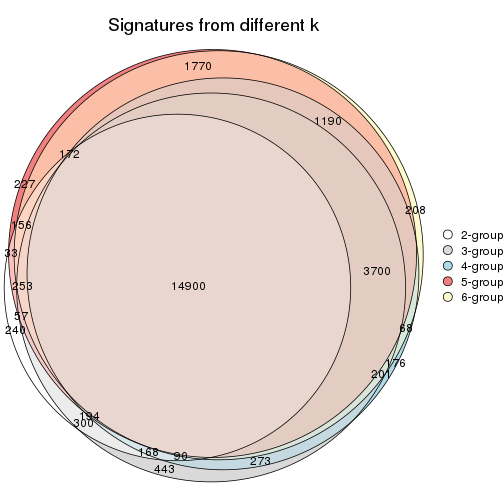
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
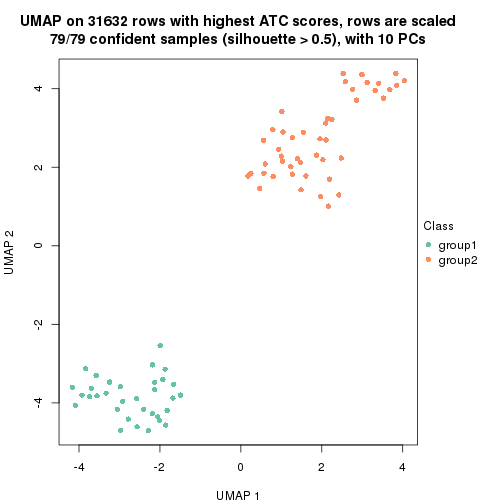
dimension_reduction(res, k = 3, method = "UMAP")
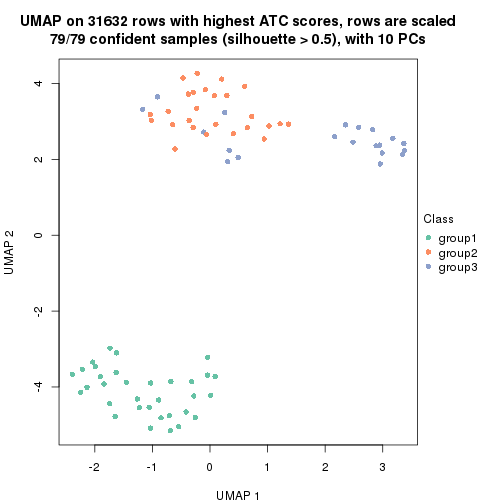
dimension_reduction(res, k = 4, method = "UMAP")
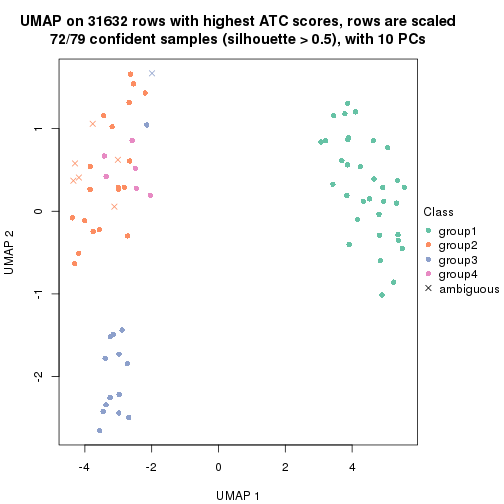
dimension_reduction(res, k = 5, method = "UMAP")
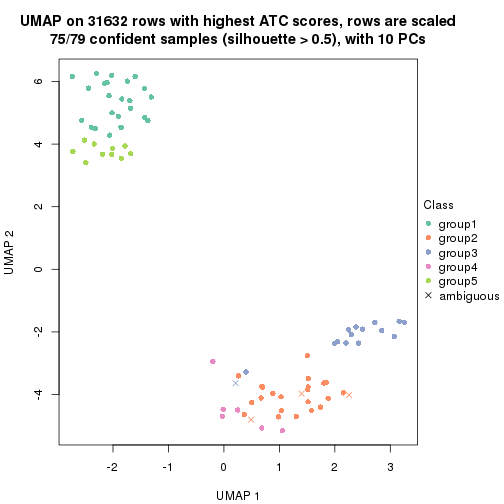
dimension_reduction(res, k = 6, method = "UMAP")
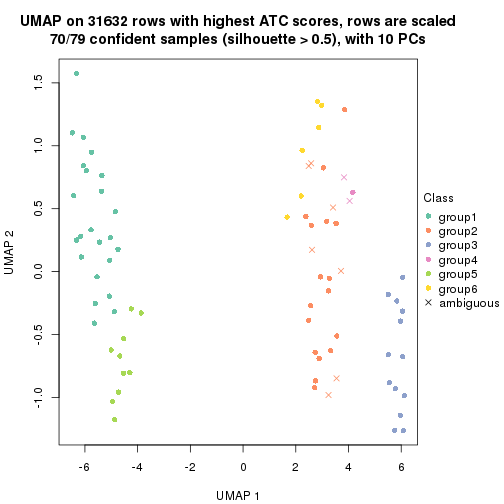
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
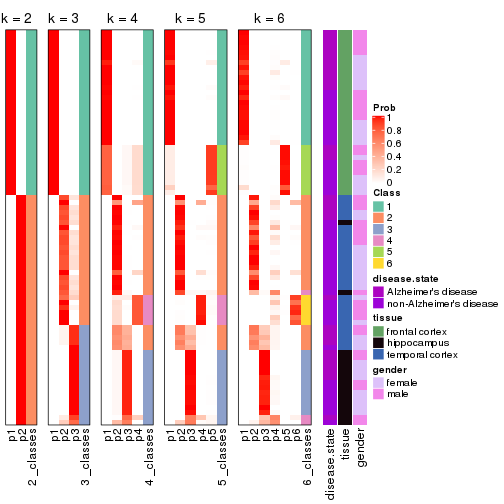
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:skmeans 79 0.5986 7.00e-18 0.984 2
#> ATC:skmeans 79 0.0687 2.64e-24 0.773 3
#> ATC:skmeans 72 0.1626 1.09e-25 0.609 4
#> ATC:skmeans 75 0.4268 1.44e-25 0.789 5
#> ATC:skmeans 70 0.4324 1.37e-23 0.597 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "pam"]
# you can also extract it by
# res = res_list["ATC:pam"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'pam' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 5.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
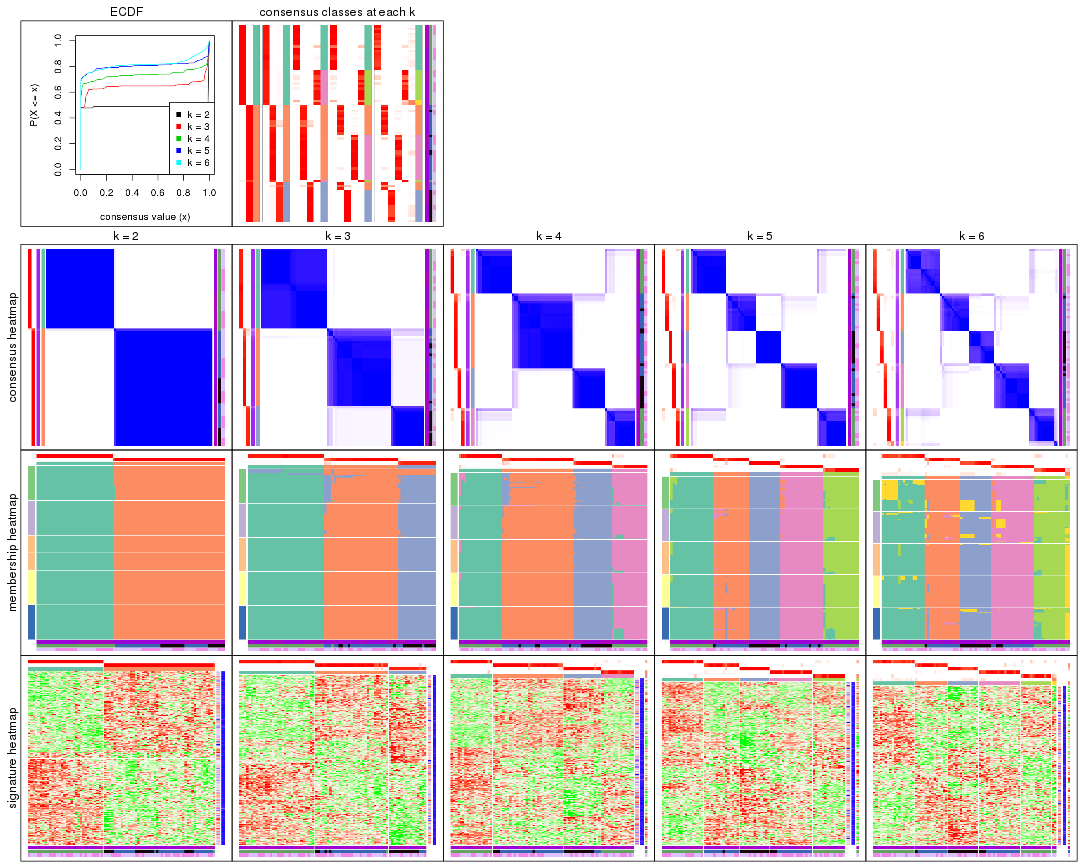
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
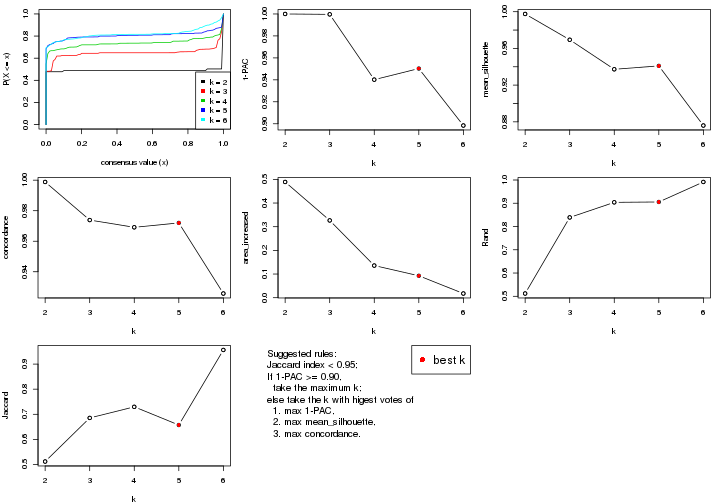
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.998 0.999 0.4891 0.512 0.512
#> 3 3 1.000 0.969 0.974 0.3266 0.839 0.685
#> 4 4 0.940 0.937 0.969 0.1359 0.904 0.730
#> 5 5 0.950 0.941 0.972 0.0927 0.906 0.657
#> 6 6 0.898 0.876 0.926 0.0178 0.992 0.956
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 5
#> attr(,"optional")
#> [1] 2 3 4
There is also optional best \(k\) = 2 3 4 that is worth to check.
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.000 0.998 0.000 1.000
#> GSM907859 2 0.000 0.998 0.000 1.000
#> GSM907860 2 0.000 0.998 0.000 1.000
#> GSM907854 2 0.000 0.998 0.000 1.000
#> GSM907855 2 0.000 0.998 0.000 1.000
#> GSM907856 2 0.000 0.998 0.000 1.000
#> GSM907857 2 0.000 0.998 0.000 1.000
#> GSM907825 2 0.000 0.998 0.000 1.000
#> GSM907828 2 0.000 0.998 0.000 1.000
#> GSM907832 2 0.000 0.998 0.000 1.000
#> GSM907833 2 0.000 0.998 0.000 1.000
#> GSM907834 2 0.000 0.998 0.000 1.000
#> GSM907826 2 0.000 0.998 0.000 1.000
#> GSM907827 2 0.000 0.998 0.000 1.000
#> GSM907829 2 0.000 0.998 0.000 1.000
#> GSM907830 2 0.000 0.998 0.000 1.000
#> GSM907831 2 0.000 0.998 0.000 1.000
#> GSM907792 1 0.000 1.000 1.000 0.000
#> GSM907795 1 0.000 1.000 1.000 0.000
#> GSM907801 1 0.000 1.000 1.000 0.000
#> GSM907802 1 0.000 1.000 1.000 0.000
#> GSM907804 1 0.000 1.000 1.000 0.000
#> GSM907805 1 0.000 1.000 1.000 0.000
#> GSM907806 1 0.000 1.000 1.000 0.000
#> GSM907793 1 0.000 1.000 1.000 0.000
#> GSM907794 1 0.000 1.000 1.000 0.000
#> GSM907796 1 0.000 1.000 1.000 0.000
#> GSM907797 1 0.000 1.000 1.000 0.000
#> GSM907798 1 0.000 1.000 1.000 0.000
#> GSM907799 1 0.000 1.000 1.000 0.000
#> GSM907800 1 0.000 1.000 1.000 0.000
#> GSM907803 1 0.000 1.000 1.000 0.000
#> GSM907864 2 0.000 0.998 0.000 1.000
#> GSM907865 2 0.000 0.998 0.000 1.000
#> GSM907868 2 0.000 0.998 0.000 1.000
#> GSM907869 2 0.000 0.998 0.000 1.000
#> GSM907870 2 0.000 0.998 0.000 1.000
#> GSM907861 2 0.000 0.998 0.000 1.000
#> GSM907862 2 0.000 0.998 0.000 1.000
#> GSM907863 2 0.000 0.998 0.000 1.000
#> GSM907866 2 0.000 0.998 0.000 1.000
#> GSM907867 2 0.000 0.998 0.000 1.000
#> GSM907839 2 0.000 0.998 0.000 1.000
#> GSM907840 2 0.000 0.998 0.000 1.000
#> GSM907842 2 0.000 0.998 0.000 1.000
#> GSM907843 2 0.000 0.998 0.000 1.000
#> GSM907845 2 0.000 0.998 0.000 1.000
#> GSM907846 2 0.000 0.998 0.000 1.000
#> GSM907848 2 0.000 0.998 0.000 1.000
#> GSM907851 2 0.000 0.998 0.000 1.000
#> GSM907835 2 0.000 0.998 0.000 1.000
#> GSM907836 2 0.000 0.998 0.000 1.000
#> GSM907837 2 0.000 0.998 0.000 1.000
#> GSM907838 2 0.000 0.998 0.000 1.000
#> GSM907841 2 0.000 0.998 0.000 1.000
#> GSM907844 2 0.000 0.998 0.000 1.000
#> GSM907847 2 0.000 0.998 0.000 1.000
#> GSM907849 2 0.000 0.998 0.000 1.000
#> GSM907850 2 0.000 0.998 0.000 1.000
#> GSM907852 2 0.000 0.998 0.000 1.000
#> GSM907853 2 0.000 0.998 0.000 1.000
#> GSM907807 1 0.000 1.000 1.000 0.000
#> GSM907813 1 0.000 1.000 1.000 0.000
#> GSM907814 1 0.000 1.000 1.000 0.000
#> GSM907816 1 0.000 1.000 1.000 0.000
#> GSM907818 1 0.000 1.000 1.000 0.000
#> GSM907819 1 0.000 1.000 1.000 0.000
#> GSM907820 1 0.000 1.000 1.000 0.000
#> GSM907822 1 0.000 1.000 1.000 0.000
#> GSM907823 1 0.000 1.000 1.000 0.000
#> GSM907808 1 0.000 1.000 1.000 0.000
#> GSM907809 1 0.000 1.000 1.000 0.000
#> GSM907810 1 0.000 1.000 1.000 0.000
#> GSM907811 1 0.000 1.000 1.000 0.000
#> GSM907812 1 0.000 1.000 1.000 0.000
#> GSM907815 1 0.000 1.000 1.000 0.000
#> GSM907817 1 0.000 1.000 1.000 0.000
#> GSM907821 1 0.000 1.000 1.000 0.000
#> GSM907824 2 0.443 0.899 0.092 0.908
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907859 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907860 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907854 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907855 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907856 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907857 3 0.1529 0.985 0.000 0.040 0.960
#> GSM907825 3 0.1964 0.973 0.000 0.056 0.944
#> GSM907828 2 0.0237 0.972 0.000 0.996 0.004
#> GSM907832 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907834 2 0.1753 0.943 0.000 0.952 0.048
#> GSM907826 2 0.0237 0.972 0.000 0.996 0.004
#> GSM907827 3 0.4235 0.829 0.000 0.176 0.824
#> GSM907829 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907830 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907831 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907792 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907795 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907801 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907802 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907804 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907805 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907806 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907793 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907794 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907796 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907797 1 0.0424 0.986 0.992 0.000 0.008
#> GSM907798 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907799 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907800 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907803 1 0.0747 0.985 0.984 0.000 0.016
#> GSM907864 2 0.0592 0.969 0.000 0.988 0.012
#> GSM907865 2 0.0592 0.969 0.000 0.988 0.012
#> GSM907868 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907869 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907870 2 0.0747 0.968 0.000 0.984 0.016
#> GSM907861 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907862 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907863 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907866 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907867 3 0.1411 0.988 0.000 0.036 0.964
#> GSM907839 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907840 2 0.0747 0.968 0.000 0.984 0.016
#> GSM907842 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907843 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907845 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907846 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907848 2 0.0237 0.972 0.000 0.996 0.004
#> GSM907851 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907835 2 0.0592 0.969 0.000 0.988 0.012
#> GSM907836 2 0.0237 0.972 0.000 0.996 0.004
#> GSM907837 2 0.4002 0.822 0.000 0.840 0.160
#> GSM907838 2 0.3941 0.827 0.000 0.844 0.156
#> GSM907841 2 0.5254 0.661 0.000 0.736 0.264
#> GSM907844 2 0.0747 0.968 0.000 0.984 0.016
#> GSM907847 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907849 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907850 2 0.0000 0.972 0.000 1.000 0.000
#> GSM907852 2 0.0747 0.968 0.000 0.984 0.016
#> GSM907853 2 0.0237 0.972 0.000 0.996 0.004
#> GSM907807 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907813 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907814 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907816 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907818 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907819 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907820 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907822 1 0.0000 0.986 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.986 1.000 0.000 0.000
#> GSM907808 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907809 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907810 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907811 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907812 1 0.0592 0.986 0.988 0.000 0.012
#> GSM907815 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907817 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907821 1 0.1031 0.984 0.976 0.000 0.024
#> GSM907824 2 0.2434 0.916 0.036 0.940 0.024
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907859 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907860 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907854 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907855 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907856 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907857 3 0.0188 0.979 0.000 0.004 0.996 0.000
#> GSM907825 3 0.0927 0.965 0.000 0.016 0.976 0.008
#> GSM907828 2 0.0524 0.969 0.000 0.988 0.004 0.008
#> GSM907832 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907833 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907834 2 0.1722 0.936 0.000 0.944 0.048 0.008
#> GSM907826 2 0.0524 0.969 0.000 0.988 0.004 0.008
#> GSM907827 3 0.3636 0.771 0.000 0.172 0.820 0.008
#> GSM907829 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907830 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907831 3 0.0524 0.975 0.000 0.004 0.988 0.008
#> GSM907792 1 0.0188 0.972 0.996 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907802 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907804 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907805 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907806 4 0.2469 0.884 0.108 0.000 0.000 0.892
#> GSM907793 1 0.0188 0.972 0.996 0.000 0.000 0.004
#> GSM907794 4 0.2704 0.870 0.124 0.000 0.000 0.876
#> GSM907796 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907797 4 0.4877 0.304 0.408 0.000 0.000 0.592
#> GSM907798 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907799 1 0.0188 0.972 0.996 0.000 0.000 0.004
#> GSM907800 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907803 1 0.4356 0.554 0.708 0.000 0.000 0.292
#> GSM907864 2 0.0188 0.970 0.000 0.996 0.004 0.000
#> GSM907865 2 0.0188 0.970 0.000 0.996 0.004 0.000
#> GSM907868 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907869 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907870 2 0.0672 0.968 0.000 0.984 0.008 0.008
#> GSM907861 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907862 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907863 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907866 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907867 3 0.0000 0.983 0.000 0.000 1.000 0.000
#> GSM907839 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907840 2 0.0672 0.968 0.000 0.984 0.008 0.008
#> GSM907842 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907843 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907845 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907846 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907848 2 0.0376 0.970 0.000 0.992 0.004 0.004
#> GSM907851 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907835 2 0.0524 0.969 0.000 0.988 0.004 0.008
#> GSM907836 2 0.0524 0.969 0.000 0.988 0.004 0.008
#> GSM907837 2 0.3852 0.779 0.000 0.800 0.192 0.008
#> GSM907838 2 0.3768 0.789 0.000 0.808 0.184 0.008
#> GSM907841 2 0.4673 0.619 0.000 0.700 0.292 0.008
#> GSM907844 2 0.0672 0.968 0.000 0.984 0.008 0.008
#> GSM907847 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907849 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907850 2 0.0000 0.971 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0672 0.968 0.000 0.984 0.008 0.008
#> GSM907853 2 0.0524 0.969 0.000 0.988 0.004 0.008
#> GSM907807 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907813 4 0.2589 0.878 0.116 0.000 0.000 0.884
#> GSM907814 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907816 1 0.0188 0.972 0.996 0.000 0.000 0.004
#> GSM907818 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907819 4 0.2011 0.903 0.080 0.000 0.000 0.920
#> GSM907820 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907822 1 0.1302 0.938 0.956 0.000 0.000 0.044
#> GSM907823 1 0.1637 0.922 0.940 0.000 0.000 0.060
#> GSM907808 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907811 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907812 1 0.0000 0.973 1.000 0.000 0.000 0.000
#> GSM907815 4 0.0469 0.937 0.012 0.000 0.000 0.988
#> GSM907817 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907821 4 0.0336 0.938 0.008 0.000 0.000 0.992
#> GSM907824 4 0.0336 0.931 0.000 0.008 0.000 0.992
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907859 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907860 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907854 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907855 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907825 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907828 4 0.2773 0.802 0.000 0.164 0.000 0.836 0.000
#> GSM907832 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907833 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907834 2 0.1121 0.940 0.000 0.956 0.000 0.044 0.000
#> GSM907826 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907827 2 0.3928 0.596 0.000 0.700 0.296 0.004 0.000
#> GSM907829 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907830 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907831 2 0.0510 0.944 0.000 0.984 0.016 0.000 0.000
#> GSM907792 1 0.0162 0.972 0.996 0.000 0.000 0.000 0.004
#> GSM907795 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907801 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907804 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907805 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907806 5 0.2074 0.882 0.104 0.000 0.000 0.000 0.896
#> GSM907793 1 0.0162 0.972 0.996 0.000 0.000 0.000 0.004
#> GSM907794 5 0.2280 0.868 0.120 0.000 0.000 0.000 0.880
#> GSM907796 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907797 5 0.4192 0.302 0.404 0.000 0.000 0.000 0.596
#> GSM907798 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907799 1 0.0162 0.972 0.996 0.000 0.000 0.000 0.004
#> GSM907800 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907803 1 0.3774 0.550 0.704 0.000 0.000 0.000 0.296
#> GSM907864 4 0.0290 0.977 0.000 0.008 0.000 0.992 0.000
#> GSM907865 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907868 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907869 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907870 2 0.2020 0.898 0.000 0.900 0.000 0.100 0.000
#> GSM907861 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907862 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907863 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907866 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.0000 1.000 0.000 0.000 1.000 0.000 0.000
#> GSM907839 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907840 2 0.0703 0.943 0.000 0.976 0.000 0.024 0.000
#> GSM907842 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907843 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907845 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907846 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907848 4 0.1965 0.889 0.000 0.096 0.000 0.904 0.000
#> GSM907851 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907835 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907836 2 0.1197 0.938 0.000 0.952 0.000 0.048 0.000
#> GSM907837 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907841 2 0.1331 0.940 0.000 0.952 0.008 0.040 0.000
#> GSM907844 2 0.0510 0.948 0.000 0.984 0.000 0.016 0.000
#> GSM907847 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907849 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907850 4 0.0000 0.983 0.000 0.000 0.000 1.000 0.000
#> GSM907852 2 0.0000 0.949 0.000 1.000 0.000 0.000 0.000
#> GSM907853 2 0.2179 0.886 0.000 0.888 0.000 0.112 0.000
#> GSM907807 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907813 5 0.2179 0.875 0.112 0.000 0.000 0.000 0.888
#> GSM907814 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907816 1 0.0162 0.972 0.996 0.000 0.000 0.000 0.004
#> GSM907818 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907819 5 0.1671 0.900 0.076 0.000 0.000 0.000 0.924
#> GSM907820 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907822 1 0.1121 0.938 0.956 0.000 0.000 0.000 0.044
#> GSM907823 1 0.1410 0.923 0.940 0.000 0.000 0.000 0.060
#> GSM907808 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907811 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907812 1 0.0000 0.973 1.000 0.000 0.000 0.000 0.000
#> GSM907815 5 0.0162 0.935 0.004 0.000 0.000 0.000 0.996
#> GSM907817 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907821 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
#> GSM907824 5 0.0000 0.936 0.000 0.000 0.000 0.000 1.000
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.0146 0.928 0.000 0.000 0.996 0.000 0.000 0.004
#> GSM907859 4 0.1267 0.920 0.000 0.000 0.000 0.940 0.000 0.060
#> GSM907860 3 0.0865 0.930 0.000 0.000 0.964 0.000 0.000 0.036
#> GSM907854 3 0.0458 0.930 0.000 0.000 0.984 0.000 0.000 0.016
#> GSM907855 3 0.0146 0.928 0.000 0.000 0.996 0.000 0.000 0.004
#> GSM907856 3 0.0146 0.928 0.000 0.000 0.996 0.000 0.000 0.004
#> GSM907857 3 0.0146 0.928 0.000 0.000 0.996 0.000 0.000 0.004
#> GSM907825 2 0.0458 0.919 0.000 0.984 0.000 0.000 0.000 0.016
#> GSM907828 4 0.3076 0.688 0.000 0.240 0.000 0.760 0.000 0.000
#> GSM907832 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907833 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907834 2 0.1245 0.913 0.000 0.952 0.000 0.032 0.000 0.016
#> GSM907826 2 0.0000 0.920 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907827 2 0.4228 0.416 0.000 0.588 0.392 0.000 0.000 0.020
#> GSM907829 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907830 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907831 2 0.0914 0.915 0.000 0.968 0.016 0.000 0.000 0.016
#> GSM907792 1 0.0260 0.917 0.992 0.000 0.000 0.000 0.000 0.008
#> GSM907795 1 0.1863 0.901 0.896 0.000 0.000 0.000 0.000 0.104
#> GSM907801 1 0.0000 0.917 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907802 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907804 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907805 1 0.1714 0.906 0.908 0.000 0.000 0.000 0.000 0.092
#> GSM907806 5 0.3738 0.568 0.208 0.000 0.000 0.000 0.752 0.040
#> GSM907793 1 0.1141 0.908 0.948 0.000 0.000 0.000 0.000 0.052
#> GSM907794 5 0.3848 0.540 0.224 0.000 0.000 0.000 0.736 0.040
#> GSM907796 1 0.0713 0.913 0.972 0.000 0.000 0.000 0.000 0.028
#> GSM907797 6 0.5047 0.748 0.136 0.000 0.000 0.000 0.236 0.628
#> GSM907798 1 0.2135 0.896 0.872 0.000 0.000 0.000 0.000 0.128
#> GSM907799 1 0.1387 0.900 0.932 0.000 0.000 0.000 0.000 0.068
#> GSM907800 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907803 1 0.3649 0.640 0.764 0.000 0.000 0.000 0.196 0.040
#> GSM907864 4 0.2520 0.847 0.000 0.004 0.000 0.844 0.000 0.152
#> GSM907865 4 0.2491 0.837 0.000 0.000 0.000 0.836 0.000 0.164
#> GSM907868 3 0.2219 0.922 0.000 0.000 0.864 0.000 0.000 0.136
#> GSM907869 3 0.2003 0.922 0.000 0.000 0.884 0.000 0.000 0.116
#> GSM907870 2 0.3991 0.730 0.000 0.756 0.000 0.088 0.000 0.156
#> GSM907861 3 0.2219 0.922 0.000 0.000 0.864 0.000 0.000 0.136
#> GSM907862 3 0.2219 0.922 0.000 0.000 0.864 0.000 0.000 0.136
#> GSM907863 3 0.2219 0.922 0.000 0.000 0.864 0.000 0.000 0.136
#> GSM907866 3 0.0146 0.928 0.000 0.000 0.996 0.000 0.000 0.004
#> GSM907867 3 0.2219 0.922 0.000 0.000 0.864 0.000 0.000 0.136
#> GSM907839 4 0.1267 0.920 0.000 0.000 0.000 0.940 0.000 0.060
#> GSM907840 2 0.0632 0.913 0.000 0.976 0.000 0.024 0.000 0.000
#> GSM907842 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907843 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907845 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907846 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907848 4 0.1863 0.858 0.000 0.104 0.000 0.896 0.000 0.000
#> GSM907851 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907835 2 0.0000 0.920 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907836 2 0.1204 0.899 0.000 0.944 0.000 0.056 0.000 0.000
#> GSM907837 2 0.0000 0.920 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907838 2 0.0000 0.920 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907841 2 0.1483 0.909 0.000 0.944 0.008 0.036 0.000 0.012
#> GSM907844 2 0.0820 0.919 0.000 0.972 0.000 0.016 0.000 0.012
#> GSM907847 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907849 4 0.0363 0.946 0.000 0.000 0.000 0.988 0.000 0.012
#> GSM907850 4 0.0000 0.947 0.000 0.000 0.000 1.000 0.000 0.000
#> GSM907852 2 0.0000 0.920 0.000 1.000 0.000 0.000 0.000 0.000
#> GSM907853 2 0.1765 0.860 0.000 0.904 0.000 0.096 0.000 0.000
#> GSM907807 1 0.0000 0.917 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907813 5 0.3523 0.616 0.180 0.000 0.000 0.000 0.780 0.040
#> GSM907814 1 0.1863 0.901 0.896 0.000 0.000 0.000 0.000 0.104
#> GSM907816 1 0.0937 0.907 0.960 0.000 0.000 0.000 0.000 0.040
#> GSM907818 5 0.0937 0.840 0.000 0.000 0.000 0.000 0.960 0.040
#> GSM907819 5 0.1794 0.810 0.036 0.000 0.000 0.000 0.924 0.040
#> GSM907820 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907822 1 0.1461 0.898 0.940 0.000 0.000 0.000 0.016 0.044
#> GSM907823 1 0.1633 0.891 0.932 0.000 0.000 0.000 0.024 0.044
#> GSM907808 1 0.1863 0.901 0.896 0.000 0.000 0.000 0.000 0.104
#> GSM907809 1 0.1863 0.901 0.896 0.000 0.000 0.000 0.000 0.104
#> GSM907810 1 0.1863 0.901 0.896 0.000 0.000 0.000 0.000 0.104
#> GSM907811 5 0.0146 0.862 0.000 0.000 0.000 0.000 0.996 0.004
#> GSM907812 1 0.0713 0.913 0.972 0.000 0.000 0.000 0.000 0.028
#> GSM907815 6 0.3684 0.700 0.000 0.000 0.000 0.000 0.372 0.628
#> GSM907817 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
#> GSM907821 5 0.0146 0.862 0.000 0.000 0.000 0.000 0.996 0.004
#> GSM907824 5 0.0000 0.863 0.000 0.000 0.000 0.000 1.000 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
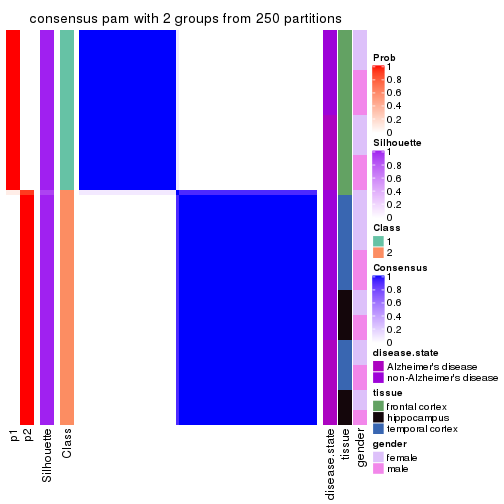
consensus_heatmap(res, k = 3)
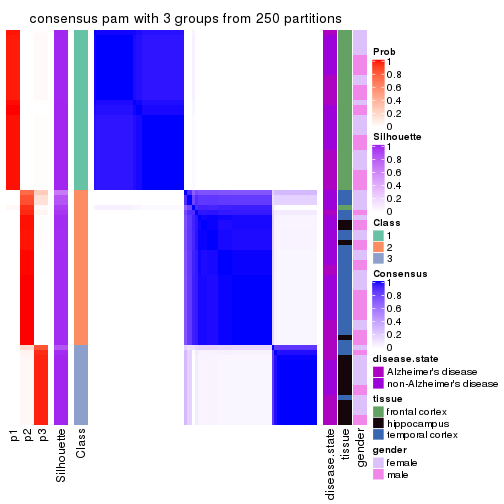
consensus_heatmap(res, k = 4)
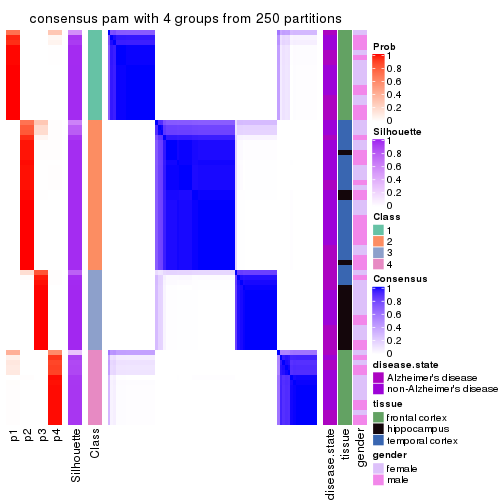
consensus_heatmap(res, k = 5)
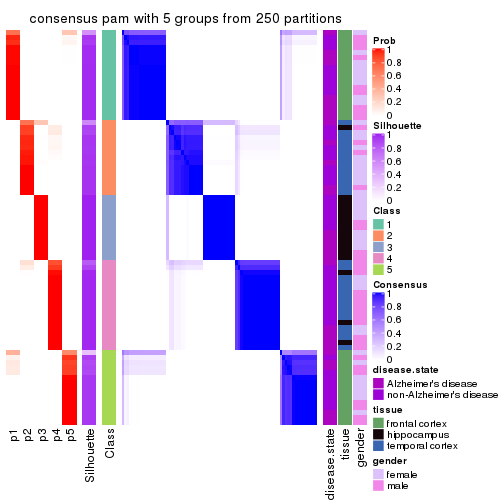
consensus_heatmap(res, k = 6)
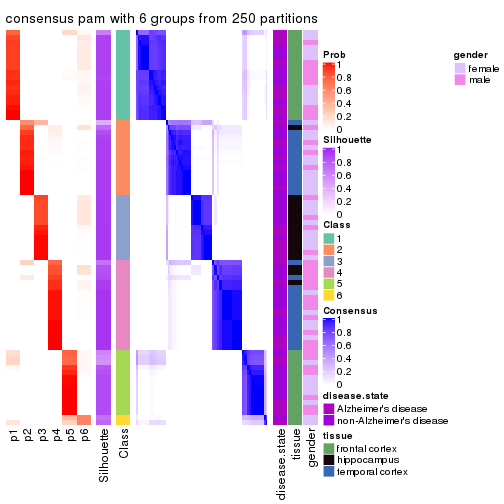
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
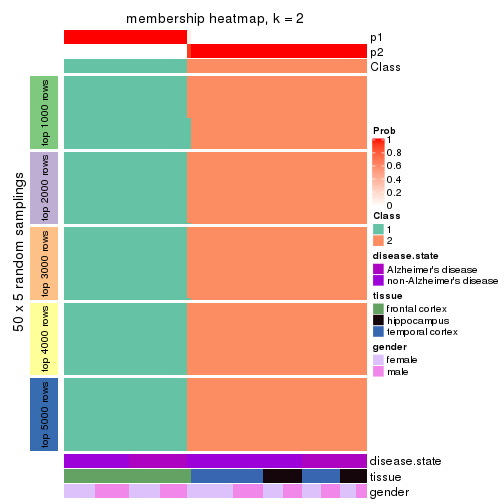
membership_heatmap(res, k = 3)
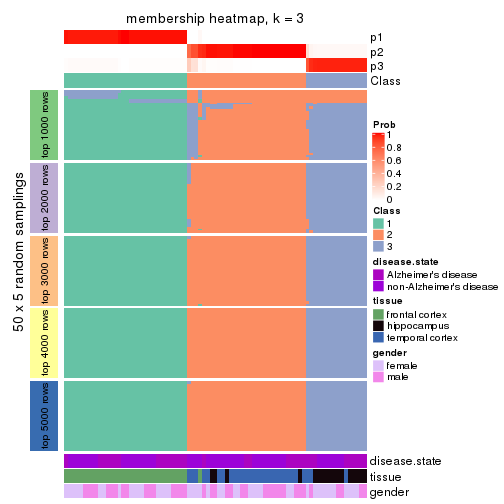
membership_heatmap(res, k = 4)
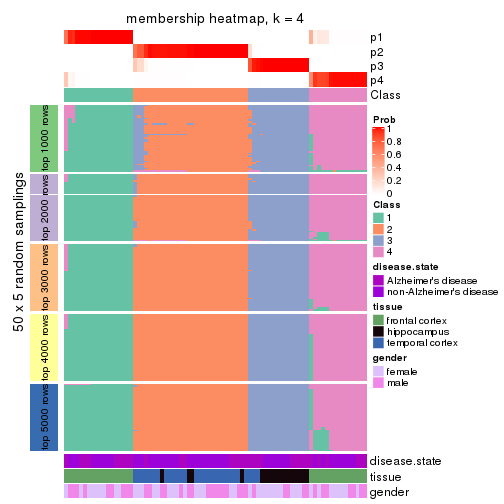
membership_heatmap(res, k = 5)
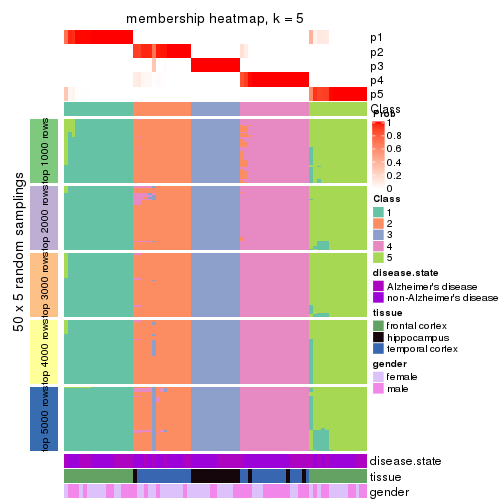
membership_heatmap(res, k = 6)
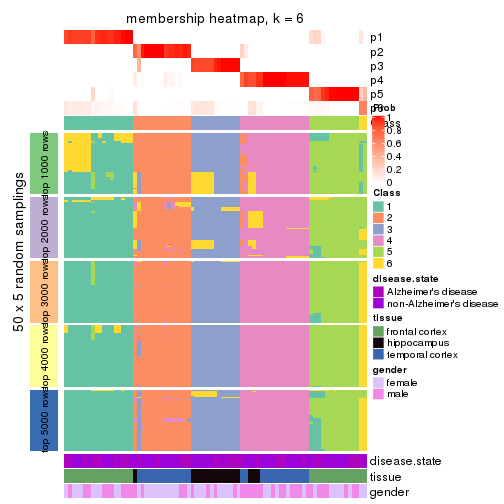
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
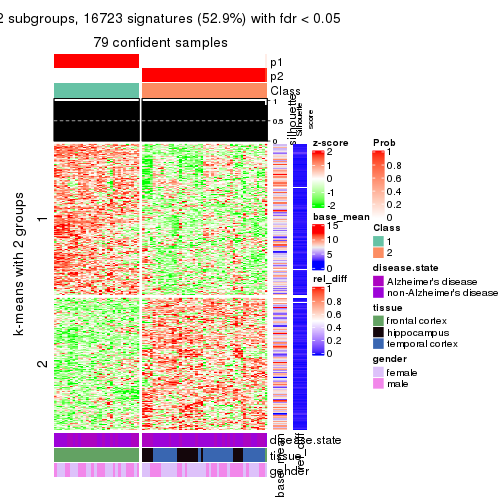
get_signatures(res, k = 3)
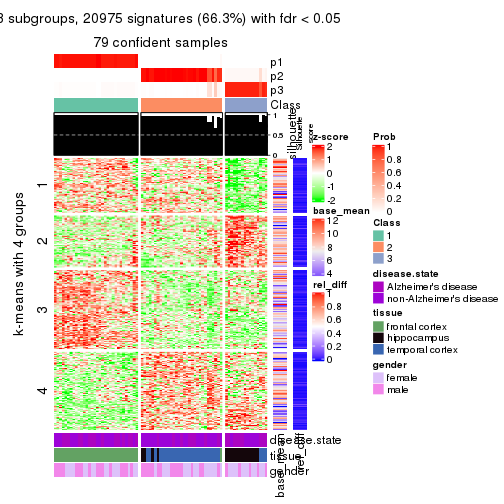
get_signatures(res, k = 4)
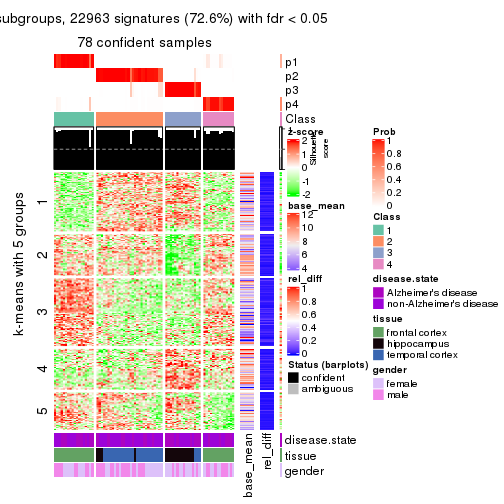
get_signatures(res, k = 5)
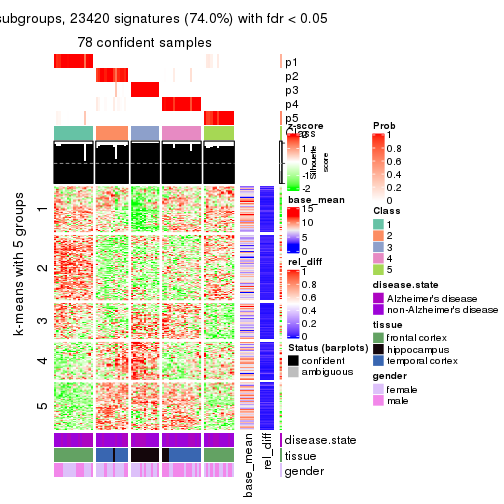
get_signatures(res, k = 6)
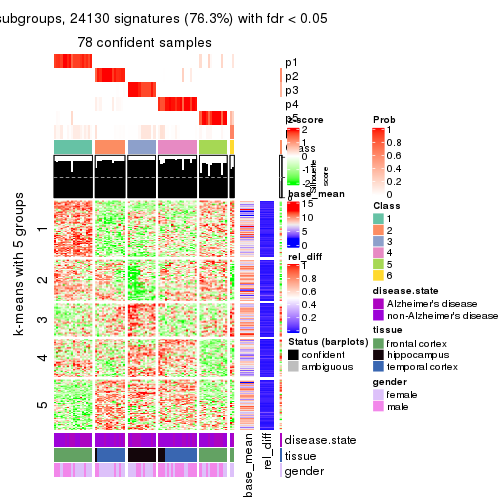
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
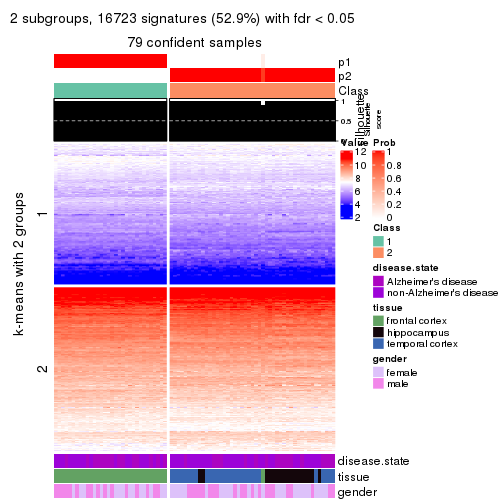
get_signatures(res, k = 3, scale_rows = FALSE)
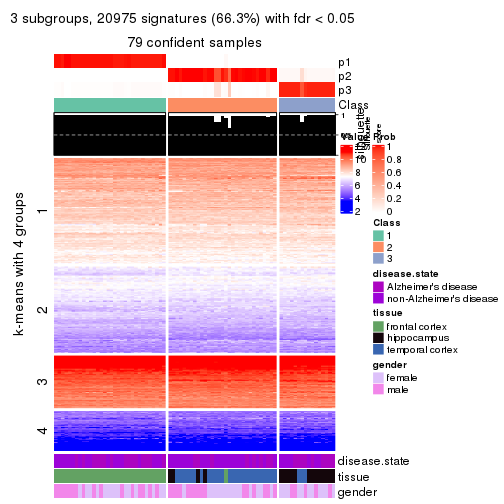
get_signatures(res, k = 4, scale_rows = FALSE)
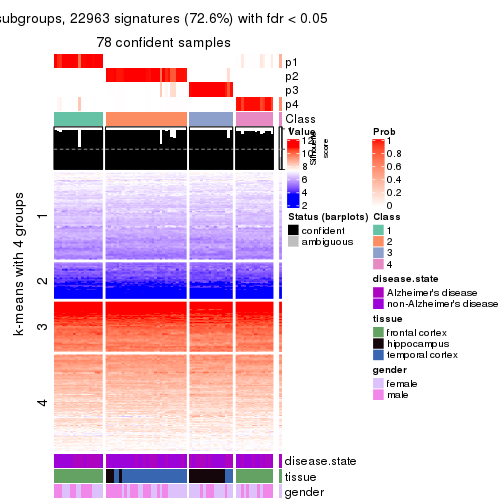
get_signatures(res, k = 5, scale_rows = FALSE)
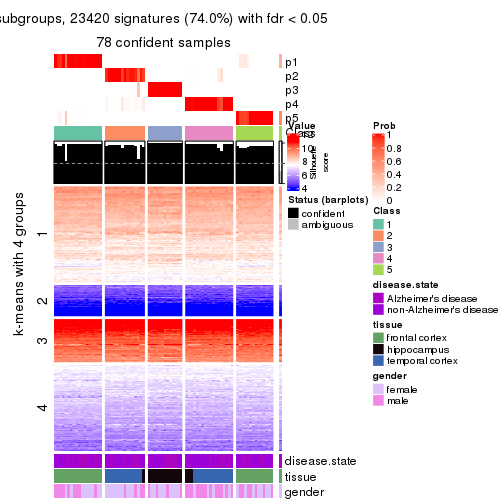
get_signatures(res, k = 6, scale_rows = FALSE)
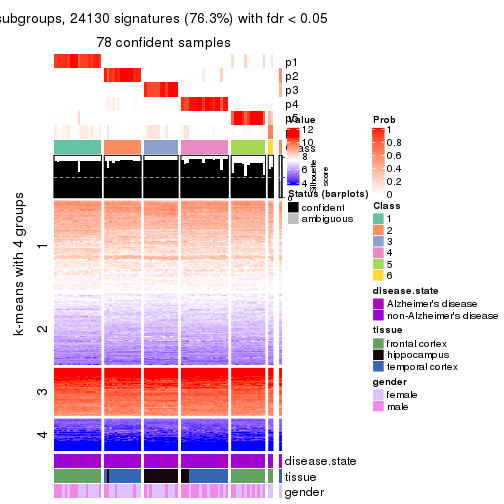
Compare the overlap of signatures from different k:
compare_signatures(res)
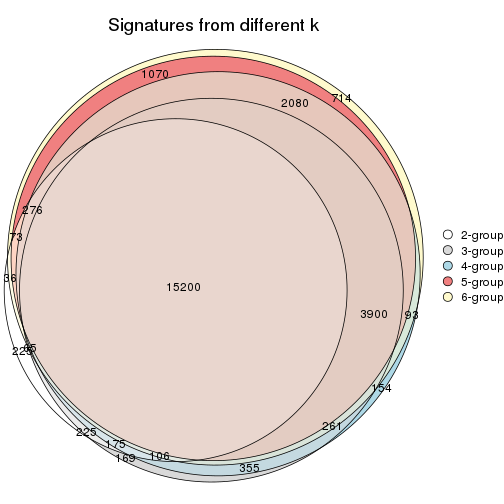
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
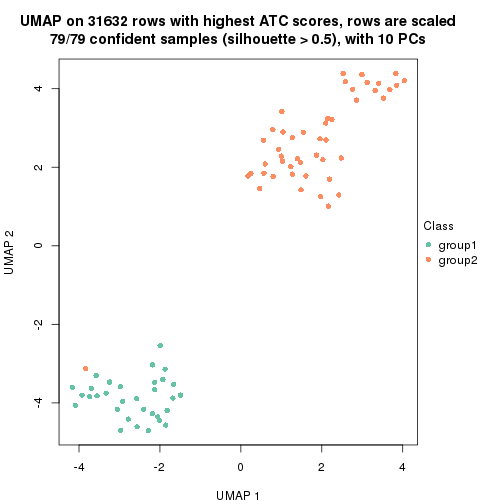
dimension_reduction(res, k = 3, method = "UMAP")
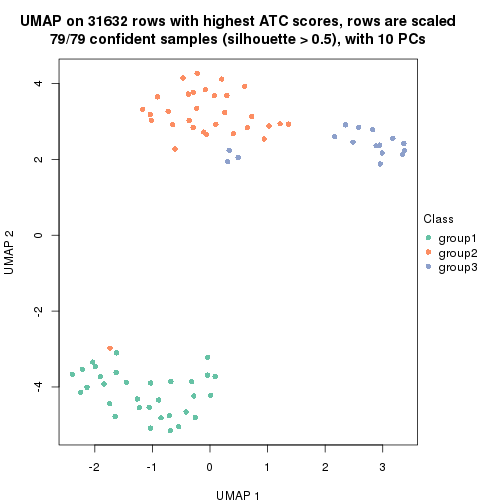
dimension_reduction(res, k = 4, method = "UMAP")
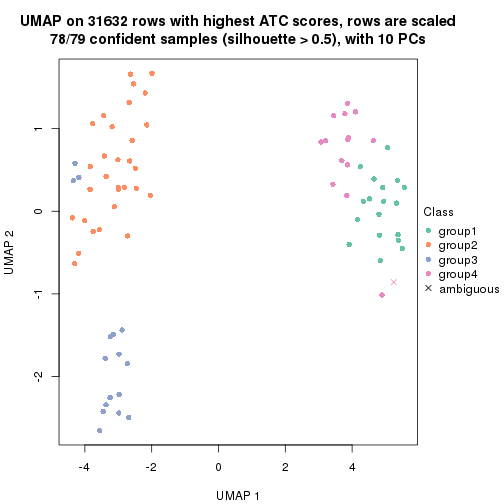
dimension_reduction(res, k = 5, method = "UMAP")
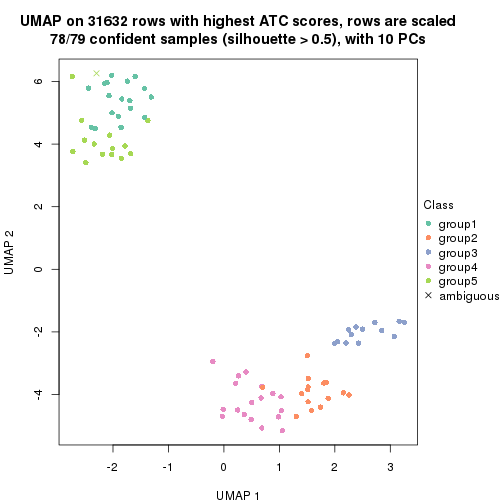
dimension_reduction(res, k = 6, method = "UMAP")
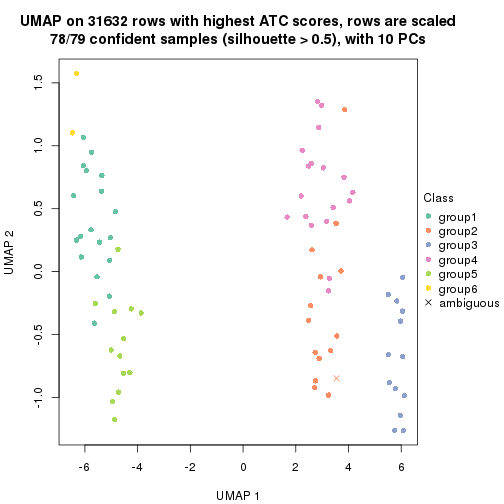
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
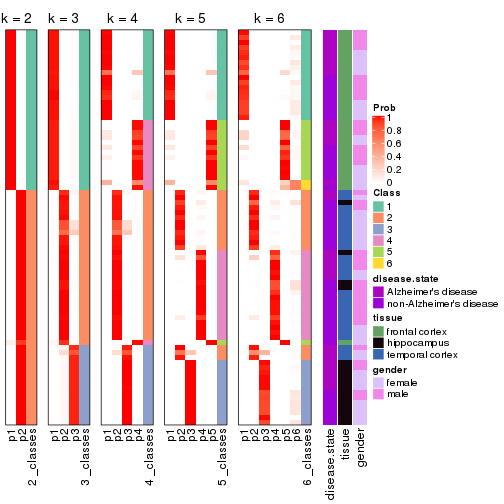
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:pam 79 0.4727 5.24e-17 0.8139 2
#> ATC:pam 79 0.0836 6.92e-23 0.3727 3
#> ATC:pam 78 0.1833 4.73e-22 0.5351 4
#> ATC:pam 78 0.7953 1.74e-24 0.0730 5
#> ATC:pam 78 0.8282 3.33e-23 0.0767 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "mclust"]
# you can also extract it by
# res = res_list["ATC:mclust"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'mclust' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
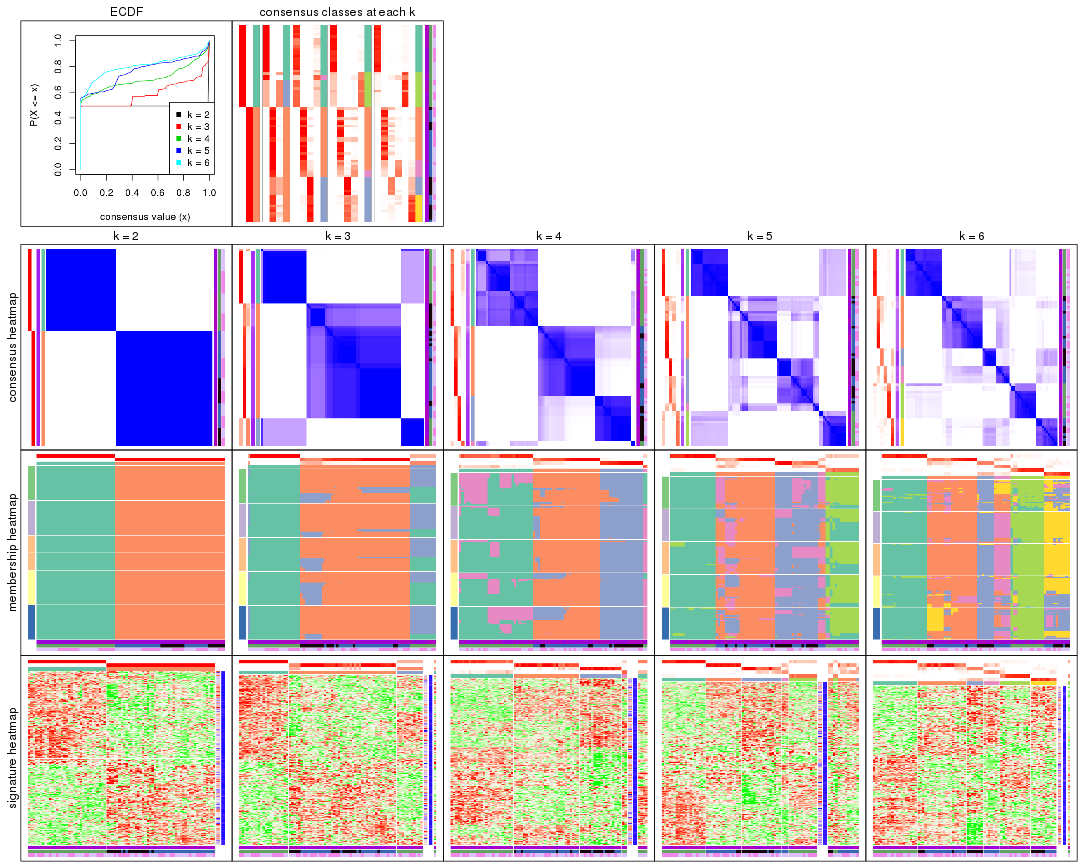
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
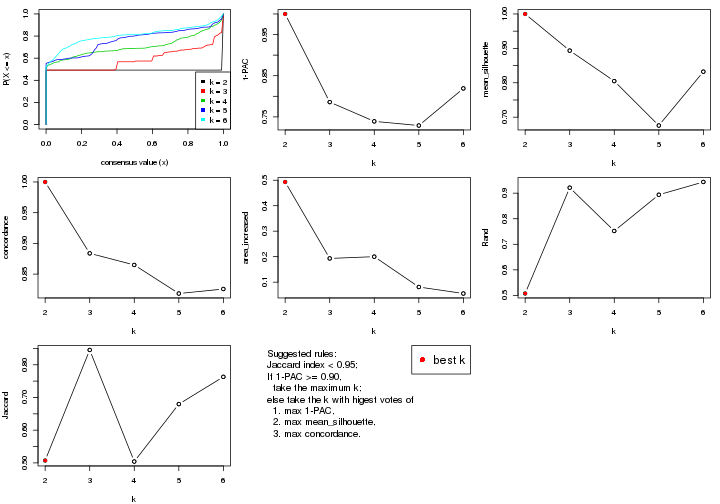
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 1.000 1.000 0.4932 0.507 0.507
#> 3 3 0.786 0.893 0.884 0.1931 0.921 0.845
#> 4 4 0.739 0.805 0.865 0.2000 0.752 0.504
#> 5 5 0.729 0.676 0.818 0.0809 0.894 0.680
#> 6 6 0.819 0.832 0.826 0.0554 0.944 0.763
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0 1 0 1
#> GSM907859 2 0 1 0 1
#> GSM907860 2 0 1 0 1
#> GSM907854 2 0 1 0 1
#> GSM907855 2 0 1 0 1
#> GSM907856 2 0 1 0 1
#> GSM907857 2 0 1 0 1
#> GSM907825 2 0 1 0 1
#> GSM907828 2 0 1 0 1
#> GSM907832 2 0 1 0 1
#> GSM907833 2 0 1 0 1
#> GSM907834 2 0 1 0 1
#> GSM907826 2 0 1 0 1
#> GSM907827 2 0 1 0 1
#> GSM907829 2 0 1 0 1
#> GSM907830 2 0 1 0 1
#> GSM907831 2 0 1 0 1
#> GSM907792 1 0 1 1 0
#> GSM907795 1 0 1 1 0
#> GSM907801 1 0 1 1 0
#> GSM907802 1 0 1 1 0
#> GSM907804 1 0 1 1 0
#> GSM907805 1 0 1 1 0
#> GSM907806 1 0 1 1 0
#> GSM907793 1 0 1 1 0
#> GSM907794 1 0 1 1 0
#> GSM907796 1 0 1 1 0
#> GSM907797 1 0 1 1 0
#> GSM907798 1 0 1 1 0
#> GSM907799 1 0 1 1 0
#> GSM907800 1 0 1 1 0
#> GSM907803 1 0 1 1 0
#> GSM907864 2 0 1 0 1
#> GSM907865 2 0 1 0 1
#> GSM907868 2 0 1 0 1
#> GSM907869 2 0 1 0 1
#> GSM907870 2 0 1 0 1
#> GSM907861 2 0 1 0 1
#> GSM907862 2 0 1 0 1
#> GSM907863 2 0 1 0 1
#> GSM907866 2 0 1 0 1
#> GSM907867 2 0 1 0 1
#> GSM907839 2 0 1 0 1
#> GSM907840 2 0 1 0 1
#> GSM907842 2 0 1 0 1
#> GSM907843 2 0 1 0 1
#> GSM907845 2 0 1 0 1
#> GSM907846 2 0 1 0 1
#> GSM907848 2 0 1 0 1
#> GSM907851 2 0 1 0 1
#> GSM907835 2 0 1 0 1
#> GSM907836 2 0 1 0 1
#> GSM907837 2 0 1 0 1
#> GSM907838 2 0 1 0 1
#> GSM907841 2 0 1 0 1
#> GSM907844 2 0 1 0 1
#> GSM907847 2 0 1 0 1
#> GSM907849 2 0 1 0 1
#> GSM907850 2 0 1 0 1
#> GSM907852 2 0 1 0 1
#> GSM907853 2 0 1 0 1
#> GSM907807 1 0 1 1 0
#> GSM907813 1 0 1 1 0
#> GSM907814 1 0 1 1 0
#> GSM907816 1 0 1 1 0
#> GSM907818 1 0 1 1 0
#> GSM907819 1 0 1 1 0
#> GSM907820 1 0 1 1 0
#> GSM907822 1 0 1 1 0
#> GSM907823 1 0 1 1 0
#> GSM907808 1 0 1 1 0
#> GSM907809 1 0 1 1 0
#> GSM907810 1 0 1 1 0
#> GSM907811 1 0 1 1 0
#> GSM907812 1 0 1 1 0
#> GSM907815 1 0 1 1 0
#> GSM907817 1 0 1 1 0
#> GSM907821 1 0 1 1 0
#> GSM907824 1 0 1 1 0
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907859 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907860 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907854 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907855 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907856 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907857 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907825 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907828 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907832 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907833 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907834 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907826 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907827 2 0.2066 0.914 0.000 0.940 0.060
#> GSM907829 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907830 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907831 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907792 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907795 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907801 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907802 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907804 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907805 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907806 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907793 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907794 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907796 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907797 1 0.0237 0.953 0.996 0.000 0.004
#> GSM907798 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907799 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907800 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907803 3 0.6140 0.986 0.404 0.000 0.596
#> GSM907864 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907865 2 0.2066 0.914 0.000 0.940 0.060
#> GSM907868 2 0.5678 0.764 0.000 0.684 0.316
#> GSM907869 2 0.3038 0.898 0.000 0.896 0.104
#> GSM907870 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907861 2 0.2066 0.914 0.000 0.940 0.060
#> GSM907862 2 0.5138 0.811 0.000 0.748 0.252
#> GSM907863 2 0.4235 0.860 0.000 0.824 0.176
#> GSM907866 2 0.6111 0.698 0.000 0.604 0.396
#> GSM907867 2 0.2878 0.902 0.000 0.904 0.096
#> GSM907839 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907840 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907842 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907843 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907845 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907846 2 0.1964 0.915 0.000 0.944 0.056
#> GSM907848 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907851 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907835 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907836 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907837 2 0.1031 0.918 0.000 0.976 0.024
#> GSM907838 2 0.1163 0.917 0.000 0.972 0.028
#> GSM907841 2 0.3267 0.893 0.000 0.884 0.116
#> GSM907844 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907847 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907849 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907850 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907852 2 0.1753 0.916 0.000 0.952 0.048
#> GSM907853 2 0.0000 0.918 0.000 1.000 0.000
#> GSM907807 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907813 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907814 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907816 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907818 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907819 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907820 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907822 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907823 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907808 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907809 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907810 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907811 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907812 1 0.0000 0.959 1.000 0.000 0.000
#> GSM907815 1 0.0237 0.953 0.996 0.000 0.004
#> GSM907817 3 0.6111 0.999 0.396 0.000 0.604
#> GSM907821 1 0.6309 -0.794 0.500 0.000 0.500
#> GSM907824 3 0.6111 0.999 0.396 0.000 0.604
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907859 2 0.3528 0.844 0.000 0.808 0.192 0.000
#> GSM907860 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907854 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907855 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907856 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907857 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907825 3 0.2011 0.921 0.000 0.080 0.920 0.000
#> GSM907828 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907832 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907833 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907834 3 0.1940 0.926 0.000 0.076 0.924 0.000
#> GSM907826 2 0.2921 0.875 0.000 0.860 0.140 0.000
#> GSM907827 3 0.1940 0.926 0.000 0.076 0.924 0.000
#> GSM907829 2 0.3208 0.871 0.000 0.848 0.148 0.004
#> GSM907830 2 0.0817 0.893 0.000 0.976 0.024 0.000
#> GSM907831 3 0.1940 0.926 0.000 0.076 0.924 0.000
#> GSM907792 1 0.1118 0.751 0.964 0.000 0.000 0.036
#> GSM907795 1 0.1716 0.739 0.936 0.000 0.000 0.064
#> GSM907801 1 0.1022 0.752 0.968 0.000 0.000 0.032
#> GSM907802 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907804 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907805 1 0.2345 0.714 0.900 0.000 0.000 0.100
#> GSM907806 1 0.1211 0.747 0.960 0.000 0.000 0.040
#> GSM907793 1 0.4697 0.247 0.644 0.000 0.000 0.356
#> GSM907794 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907796 1 0.4697 0.247 0.644 0.000 0.000 0.356
#> GSM907797 4 0.3837 1.000 0.224 0.000 0.000 0.776
#> GSM907798 1 0.4697 0.247 0.644 0.000 0.000 0.356
#> GSM907799 1 0.3688 0.576 0.792 0.000 0.000 0.208
#> GSM907800 1 0.4941 0.534 0.564 0.000 0.000 0.436
#> GSM907803 1 0.3764 0.726 0.784 0.000 0.000 0.216
#> GSM907864 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907865 2 0.3486 0.847 0.000 0.812 0.188 0.000
#> GSM907868 3 0.0188 0.965 0.000 0.004 0.996 0.000
#> GSM907869 3 0.1022 0.958 0.000 0.032 0.968 0.000
#> GSM907870 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907861 3 0.1302 0.951 0.000 0.044 0.956 0.000
#> GSM907862 3 0.0188 0.965 0.000 0.004 0.996 0.000
#> GSM907863 3 0.0188 0.965 0.000 0.004 0.996 0.000
#> GSM907866 3 0.0000 0.964 0.000 0.000 1.000 0.000
#> GSM907867 3 0.0921 0.960 0.000 0.028 0.972 0.000
#> GSM907839 2 0.0188 0.891 0.000 0.996 0.004 0.000
#> GSM907840 2 0.2647 0.882 0.000 0.880 0.120 0.000
#> GSM907842 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907843 2 0.0592 0.892 0.000 0.984 0.016 0.000
#> GSM907845 2 0.3208 0.871 0.000 0.848 0.148 0.004
#> GSM907846 2 0.3391 0.870 0.004 0.844 0.148 0.004
#> GSM907848 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907851 2 0.1474 0.891 0.000 0.948 0.052 0.000
#> GSM907835 2 0.2760 0.880 0.000 0.872 0.128 0.000
#> GSM907836 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907837 2 0.4072 0.764 0.000 0.748 0.252 0.000
#> GSM907838 2 0.4564 0.643 0.000 0.672 0.328 0.000
#> GSM907841 3 0.1022 0.958 0.000 0.032 0.968 0.000
#> GSM907844 2 0.2973 0.874 0.000 0.856 0.144 0.000
#> GSM907847 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907849 2 0.2814 0.879 0.000 0.868 0.132 0.000
#> GSM907850 2 0.0000 0.890 0.000 1.000 0.000 0.000
#> GSM907852 2 0.4790 0.534 0.000 0.620 0.380 0.000
#> GSM907853 2 0.0188 0.891 0.000 0.996 0.004 0.000
#> GSM907807 1 0.2469 0.705 0.892 0.000 0.000 0.108
#> GSM907813 1 0.1557 0.742 0.944 0.000 0.000 0.056
#> GSM907814 1 0.1637 0.736 0.940 0.000 0.000 0.060
#> GSM907816 1 0.0469 0.756 0.988 0.000 0.000 0.012
#> GSM907818 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907819 1 0.3975 0.716 0.760 0.000 0.000 0.240
#> GSM907820 1 0.3764 0.726 0.784 0.000 0.000 0.216
#> GSM907822 1 0.1637 0.736 0.940 0.000 0.000 0.060
#> GSM907823 1 0.1637 0.736 0.940 0.000 0.000 0.060
#> GSM907808 1 0.1474 0.745 0.948 0.000 0.000 0.052
#> GSM907809 1 0.1302 0.748 0.956 0.000 0.000 0.044
#> GSM907810 1 0.1022 0.753 0.968 0.000 0.000 0.032
#> GSM907811 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907812 1 0.4679 0.259 0.648 0.000 0.000 0.352
#> GSM907815 4 0.3837 1.000 0.224 0.000 0.000 0.776
#> GSM907817 1 0.3907 0.719 0.768 0.000 0.000 0.232
#> GSM907821 1 0.2973 0.745 0.856 0.000 0.000 0.144
#> GSM907824 1 0.3764 0.726 0.784 0.000 0.000 0.216
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907859 2 0.6636 0.143 0.000 0.452 0.264 0.284 0.000
#> GSM907860 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907854 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907855 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907856 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907857 3 0.1544 0.699 0.000 0.000 0.932 0.068 0.000
#> GSM907825 3 0.5983 0.337 0.000 0.116 0.504 0.380 0.000
#> GSM907828 2 0.0703 0.672 0.000 0.976 0.000 0.024 0.000
#> GSM907832 2 0.0703 0.672 0.000 0.976 0.000 0.024 0.000
#> GSM907833 2 0.0703 0.672 0.000 0.976 0.000 0.024 0.000
#> GSM907834 3 0.4980 0.577 0.000 0.036 0.584 0.380 0.000
#> GSM907826 2 0.4902 -0.595 0.000 0.508 0.024 0.468 0.000
#> GSM907827 3 0.4313 0.657 0.000 0.008 0.636 0.356 0.000
#> GSM907829 2 0.6729 0.108 0.000 0.396 0.256 0.348 0.000
#> GSM907830 2 0.1478 0.647 0.000 0.936 0.000 0.064 0.000
#> GSM907831 3 0.5176 0.550 0.000 0.048 0.572 0.380 0.000
#> GSM907792 1 0.0404 0.968 0.988 0.000 0.000 0.000 0.012
#> GSM907795 1 0.0162 0.968 0.996 0.000 0.000 0.000 0.004
#> GSM907801 1 0.0290 0.969 0.992 0.000 0.000 0.000 0.008
#> GSM907802 5 0.3612 0.863 0.268 0.000 0.000 0.000 0.732
#> GSM907804 5 0.3612 0.863 0.268 0.000 0.000 0.000 0.732
#> GSM907805 1 0.0162 0.969 0.996 0.000 0.000 0.000 0.004
#> GSM907806 1 0.1544 0.939 0.932 0.000 0.000 0.000 0.068
#> GSM907793 1 0.0290 0.968 0.992 0.000 0.000 0.000 0.008
#> GSM907794 5 0.3661 0.861 0.276 0.000 0.000 0.000 0.724
#> GSM907796 1 0.0290 0.968 0.992 0.000 0.000 0.000 0.008
#> GSM907797 5 0.5655 0.361 0.288 0.000 0.000 0.112 0.600
#> GSM907798 1 0.0290 0.968 0.992 0.000 0.000 0.000 0.008
#> GSM907799 1 0.0404 0.968 0.988 0.000 0.000 0.000 0.012
#> GSM907800 5 0.3612 0.863 0.268 0.000 0.000 0.000 0.732
#> GSM907803 5 0.4192 0.691 0.404 0.000 0.000 0.000 0.596
#> GSM907864 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907865 2 0.5899 0.260 0.000 0.592 0.248 0.160 0.000
#> GSM907868 3 0.3109 0.772 0.000 0.000 0.800 0.200 0.000
#> GSM907869 3 0.3534 0.757 0.000 0.000 0.744 0.256 0.000
#> GSM907870 2 0.0794 0.670 0.000 0.972 0.000 0.028 0.000
#> GSM907861 3 0.4419 0.707 0.000 0.020 0.668 0.312 0.000
#> GSM907862 3 0.3210 0.772 0.000 0.000 0.788 0.212 0.000
#> GSM907863 3 0.3242 0.771 0.000 0.000 0.784 0.216 0.000
#> GSM907866 3 0.0000 0.747 0.000 0.000 1.000 0.000 0.000
#> GSM907867 3 0.3636 0.750 0.000 0.000 0.728 0.272 0.000
#> GSM907839 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907840 2 0.4441 0.103 0.000 0.720 0.044 0.236 0.000
#> GSM907842 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907843 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907845 2 0.6729 0.108 0.000 0.396 0.256 0.348 0.000
#> GSM907846 2 0.6712 0.123 0.000 0.412 0.256 0.332 0.000
#> GSM907848 2 0.0703 0.672 0.000 0.976 0.000 0.024 0.000
#> GSM907851 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907835 2 0.4297 -0.531 0.000 0.528 0.000 0.472 0.000
#> GSM907836 2 0.0703 0.672 0.000 0.976 0.000 0.024 0.000
#> GSM907837 4 0.5331 0.832 0.000 0.372 0.060 0.568 0.000
#> GSM907838 4 0.5284 0.826 0.000 0.376 0.056 0.568 0.000
#> GSM907841 3 0.3534 0.759 0.000 0.000 0.744 0.256 0.000
#> GSM907844 2 0.5818 -0.699 0.000 0.464 0.092 0.444 0.000
#> GSM907847 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907849 2 0.3160 0.449 0.000 0.808 0.188 0.004 0.000
#> GSM907850 2 0.0162 0.672 0.000 0.996 0.000 0.004 0.000
#> GSM907852 4 0.6225 0.680 0.000 0.256 0.200 0.544 0.000
#> GSM907853 2 0.1197 0.659 0.000 0.952 0.000 0.048 0.000
#> GSM907807 1 0.0162 0.969 0.996 0.000 0.000 0.000 0.004
#> GSM907813 1 0.1478 0.940 0.936 0.000 0.000 0.000 0.064
#> GSM907814 1 0.1478 0.940 0.936 0.000 0.000 0.000 0.064
#> GSM907816 1 0.1121 0.943 0.956 0.000 0.000 0.000 0.044
#> GSM907818 5 0.3661 0.861 0.276 0.000 0.000 0.000 0.724
#> GSM907819 5 0.3661 0.861 0.276 0.000 0.000 0.000 0.724
#> GSM907820 5 0.3707 0.837 0.284 0.000 0.000 0.000 0.716
#> GSM907822 1 0.1478 0.940 0.936 0.000 0.000 0.000 0.064
#> GSM907823 1 0.1478 0.940 0.936 0.000 0.000 0.000 0.064
#> GSM907808 1 0.0000 0.969 1.000 0.000 0.000 0.000 0.000
#> GSM907809 1 0.0162 0.968 0.996 0.000 0.000 0.000 0.004
#> GSM907810 1 0.0162 0.970 0.996 0.000 0.000 0.000 0.004
#> GSM907811 5 0.3612 0.863 0.268 0.000 0.000 0.000 0.732
#> GSM907812 1 0.0290 0.968 0.992 0.000 0.000 0.000 0.008
#> GSM907815 5 0.5655 0.361 0.288 0.000 0.000 0.112 0.600
#> GSM907817 5 0.3612 0.863 0.268 0.000 0.000 0.000 0.732
#> GSM907821 5 0.4015 0.772 0.348 0.000 0.000 0.000 0.652
#> GSM907824 5 0.3143 0.795 0.204 0.000 0.000 0.000 0.796
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.3647 0.956 0.000 0.000 0.640 0.000 0.000 0.360
#> GSM907859 2 0.5081 0.609 0.000 0.552 0.376 0.064 0.000 0.008
#> GSM907860 3 0.3714 0.945 0.000 0.000 0.656 0.004 0.000 0.340
#> GSM907854 3 0.3659 0.950 0.000 0.000 0.636 0.000 0.000 0.364
#> GSM907855 3 0.3647 0.956 0.000 0.000 0.640 0.000 0.000 0.360
#> GSM907856 3 0.3634 0.956 0.000 0.000 0.644 0.000 0.000 0.356
#> GSM907857 3 0.5112 0.797 0.000 0.000 0.592 0.112 0.000 0.296
#> GSM907825 6 0.4094 0.726 0.000 0.028 0.044 0.160 0.000 0.768
#> GSM907828 2 0.0260 0.787 0.000 0.992 0.000 0.008 0.000 0.000
#> GSM907832 2 0.0622 0.790 0.000 0.980 0.012 0.008 0.000 0.000
#> GSM907833 2 0.0260 0.787 0.000 0.992 0.000 0.008 0.000 0.000
#> GSM907834 6 0.3669 0.752 0.000 0.016 0.044 0.140 0.000 0.800
#> GSM907826 4 0.4958 0.823 0.000 0.364 0.000 0.560 0.000 0.076
#> GSM907827 6 0.1391 0.824 0.000 0.000 0.016 0.040 0.000 0.944
#> GSM907829 2 0.5867 0.558 0.000 0.616 0.208 0.076 0.000 0.100
#> GSM907830 2 0.0972 0.780 0.000 0.964 0.008 0.028 0.000 0.000
#> GSM907831 6 0.4094 0.726 0.000 0.028 0.044 0.160 0.000 0.768
#> GSM907792 1 0.1141 0.958 0.948 0.000 0.000 0.000 0.052 0.000
#> GSM907795 1 0.0260 0.966 0.992 0.000 0.000 0.000 0.008 0.000
#> GSM907801 1 0.1007 0.963 0.956 0.000 0.000 0.000 0.044 0.000
#> GSM907802 5 0.0937 0.892 0.040 0.000 0.000 0.000 0.960 0.000
#> GSM907804 5 0.0937 0.892 0.040 0.000 0.000 0.000 0.960 0.000
#> GSM907805 1 0.0547 0.970 0.980 0.000 0.000 0.000 0.020 0.000
#> GSM907806 1 0.1434 0.948 0.940 0.000 0.012 0.000 0.048 0.000
#> GSM907793 1 0.0713 0.970 0.972 0.000 0.000 0.000 0.028 0.000
#> GSM907794 5 0.1327 0.888 0.064 0.000 0.000 0.000 0.936 0.000
#> GSM907796 1 0.0713 0.970 0.972 0.000 0.000 0.000 0.028 0.000
#> GSM907797 5 0.5467 0.613 0.048 0.000 0.076 0.248 0.628 0.000
#> GSM907798 1 0.0632 0.970 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907799 1 0.1075 0.961 0.952 0.000 0.000 0.000 0.048 0.000
#> GSM907800 5 0.1141 0.892 0.052 0.000 0.000 0.000 0.948 0.000
#> GSM907803 5 0.3817 0.252 0.432 0.000 0.000 0.000 0.568 0.000
#> GSM907864 2 0.3133 0.757 0.000 0.780 0.212 0.008 0.000 0.000
#> GSM907865 2 0.4664 0.651 0.000 0.596 0.356 0.044 0.000 0.004
#> GSM907868 6 0.1765 0.768 0.000 0.000 0.096 0.000 0.000 0.904
#> GSM907869 6 0.2313 0.779 0.000 0.004 0.100 0.012 0.000 0.884
#> GSM907870 2 0.0363 0.785 0.000 0.988 0.000 0.012 0.000 0.000
#> GSM907861 6 0.3399 0.744 0.000 0.088 0.064 0.016 0.000 0.832
#> GSM907862 6 0.1219 0.815 0.000 0.000 0.048 0.004 0.000 0.948
#> GSM907863 6 0.1082 0.816 0.000 0.000 0.040 0.004 0.000 0.956
#> GSM907866 3 0.3634 0.956 0.000 0.000 0.644 0.000 0.000 0.356
#> GSM907867 6 0.1141 0.812 0.000 0.000 0.052 0.000 0.000 0.948
#> GSM907839 2 0.3368 0.753 0.000 0.756 0.232 0.012 0.000 0.000
#> GSM907840 4 0.5325 0.793 0.000 0.388 0.008 0.520 0.000 0.084
#> GSM907842 2 0.1204 0.794 0.000 0.944 0.056 0.000 0.000 0.000
#> GSM907843 2 0.3298 0.753 0.000 0.756 0.236 0.008 0.000 0.000
#> GSM907845 2 0.5842 0.562 0.000 0.620 0.204 0.076 0.000 0.100
#> GSM907846 2 0.5655 0.577 0.000 0.644 0.180 0.064 0.000 0.112
#> GSM907848 2 0.0260 0.787 0.000 0.992 0.000 0.008 0.000 0.000
#> GSM907851 2 0.3298 0.753 0.000 0.756 0.236 0.008 0.000 0.000
#> GSM907835 4 0.4985 0.815 0.000 0.376 0.000 0.548 0.000 0.076
#> GSM907836 2 0.0260 0.787 0.000 0.992 0.000 0.008 0.000 0.000
#> GSM907837 4 0.4687 0.839 0.000 0.180 0.000 0.684 0.000 0.136
#> GSM907838 4 0.4687 0.839 0.000 0.180 0.000 0.684 0.000 0.136
#> GSM907841 6 0.0717 0.823 0.000 0.000 0.016 0.008 0.000 0.976
#> GSM907844 4 0.5100 0.856 0.000 0.260 0.000 0.612 0.000 0.128
#> GSM907847 2 0.2234 0.789 0.000 0.872 0.124 0.004 0.000 0.000
#> GSM907849 2 0.3834 0.743 0.000 0.728 0.244 0.024 0.000 0.004
#> GSM907850 2 0.1267 0.793 0.000 0.940 0.060 0.000 0.000 0.000
#> GSM907852 4 0.4806 0.817 0.000 0.164 0.004 0.684 0.000 0.148
#> GSM907853 2 0.0632 0.782 0.000 0.976 0.000 0.024 0.000 0.000
#> GSM907807 1 0.0632 0.970 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907813 1 0.1461 0.945 0.940 0.000 0.016 0.000 0.044 0.000
#> GSM907814 1 0.1320 0.948 0.948 0.000 0.016 0.000 0.036 0.000
#> GSM907816 1 0.1141 0.960 0.948 0.000 0.000 0.000 0.052 0.000
#> GSM907818 5 0.1075 0.893 0.048 0.000 0.000 0.000 0.952 0.000
#> GSM907819 5 0.1075 0.891 0.048 0.000 0.000 0.000 0.952 0.000
#> GSM907820 5 0.1141 0.883 0.052 0.000 0.000 0.000 0.948 0.000
#> GSM907822 1 0.1391 0.947 0.944 0.000 0.016 0.000 0.040 0.000
#> GSM907823 1 0.1391 0.947 0.944 0.000 0.016 0.000 0.040 0.000
#> GSM907808 1 0.0632 0.969 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907809 1 0.0000 0.963 1.000 0.000 0.000 0.000 0.000 0.000
#> GSM907810 1 0.0632 0.969 0.976 0.000 0.000 0.000 0.024 0.000
#> GSM907811 5 0.1007 0.892 0.044 0.000 0.000 0.000 0.956 0.000
#> GSM907812 1 0.0713 0.970 0.972 0.000 0.000 0.000 0.028 0.000
#> GSM907815 5 0.5467 0.613 0.048 0.000 0.076 0.248 0.628 0.000
#> GSM907817 5 0.0865 0.891 0.036 0.000 0.000 0.000 0.964 0.000
#> GSM907821 5 0.1863 0.847 0.104 0.000 0.000 0.000 0.896 0.000
#> GSM907824 5 0.0790 0.886 0.032 0.000 0.000 0.000 0.968 0.000
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
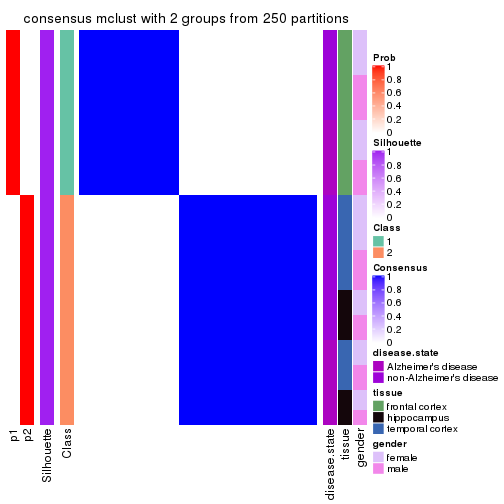
consensus_heatmap(res, k = 3)
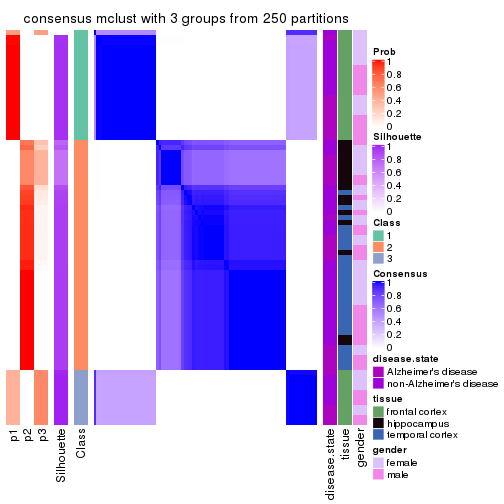
consensus_heatmap(res, k = 4)
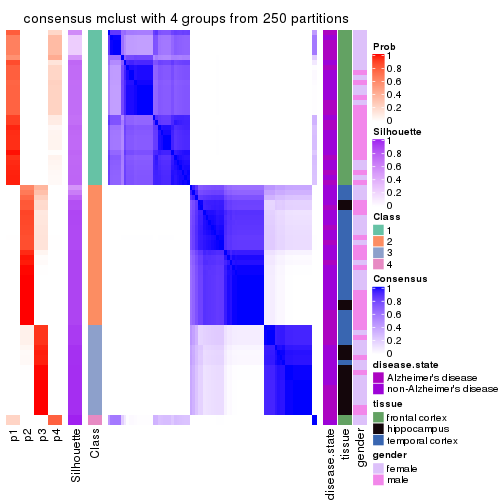
consensus_heatmap(res, k = 5)
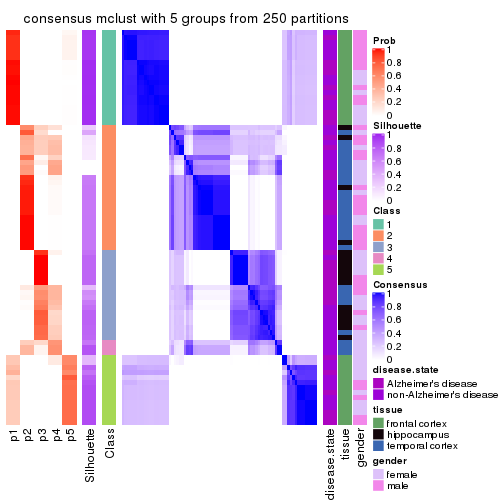
consensus_heatmap(res, k = 6)
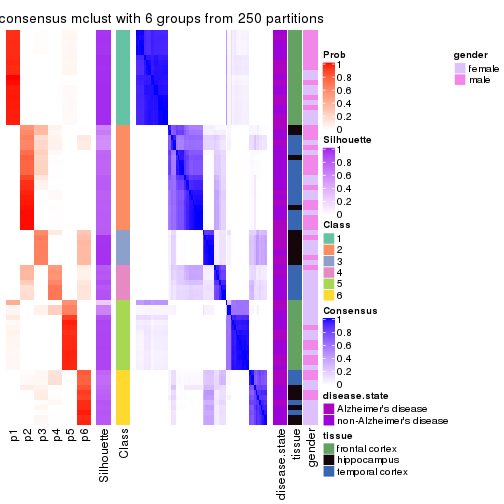
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
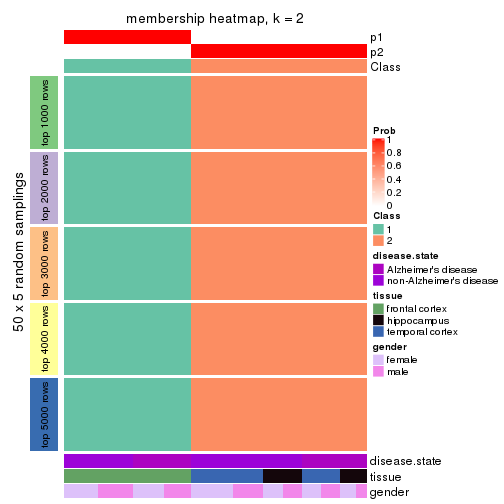
membership_heatmap(res, k = 3)
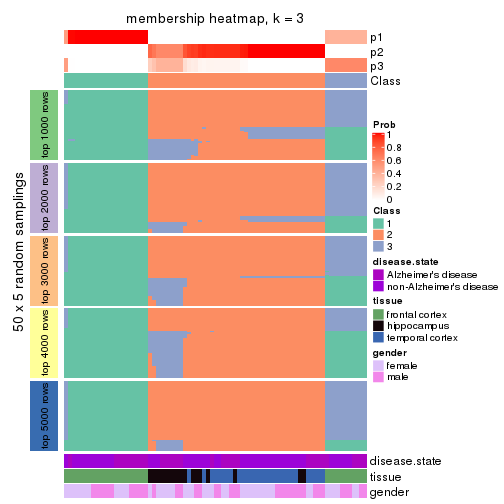
membership_heatmap(res, k = 4)
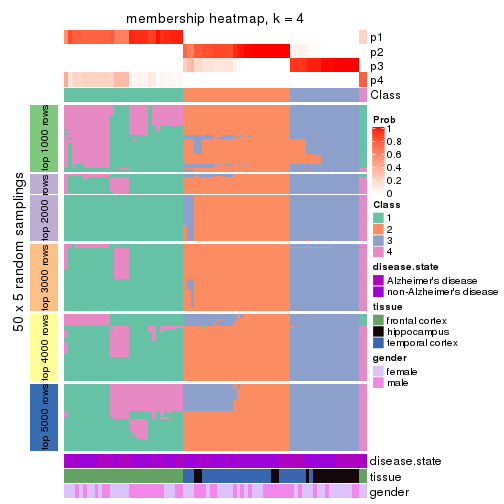
membership_heatmap(res, k = 5)
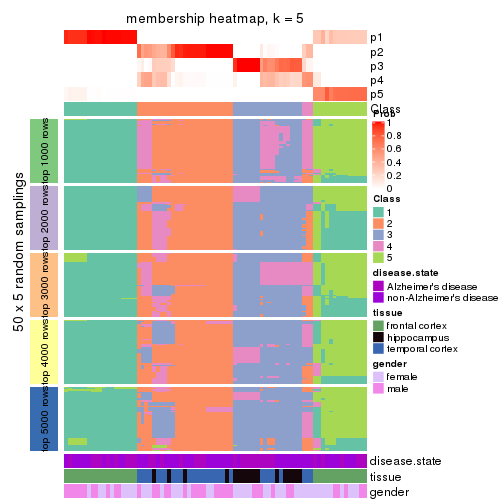
membership_heatmap(res, k = 6)
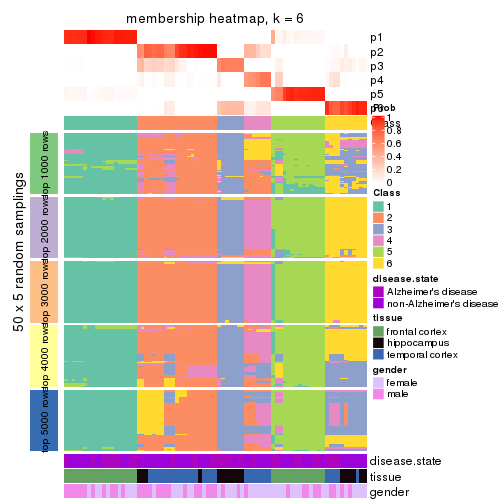
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
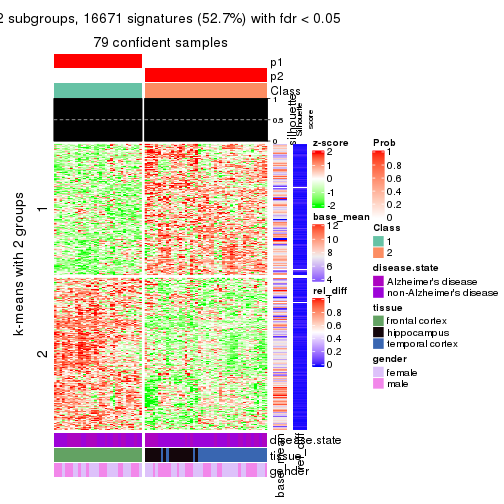
get_signatures(res, k = 3)
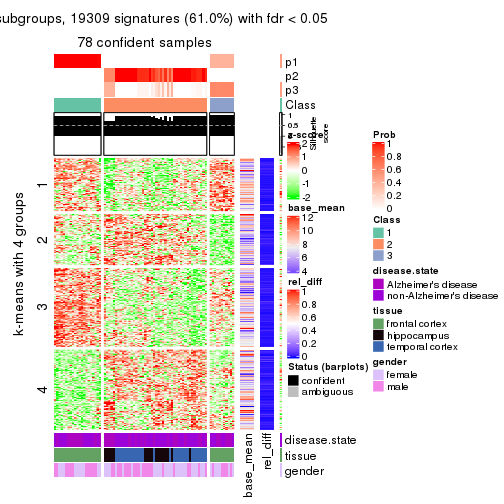
get_signatures(res, k = 4)
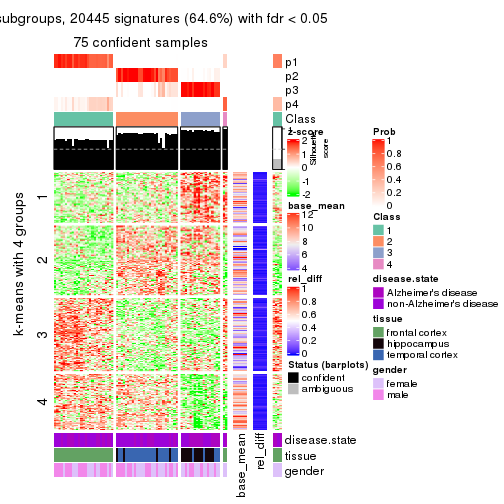
get_signatures(res, k = 5)
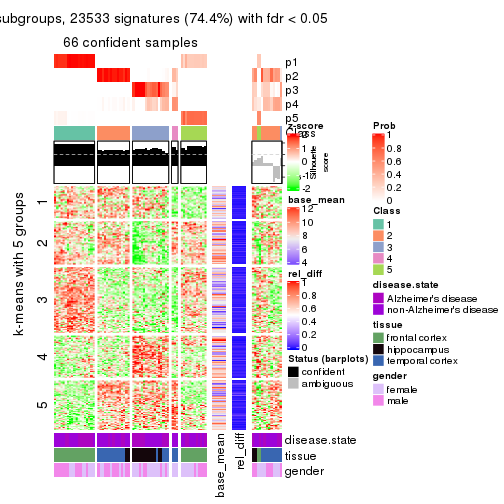
get_signatures(res, k = 6)
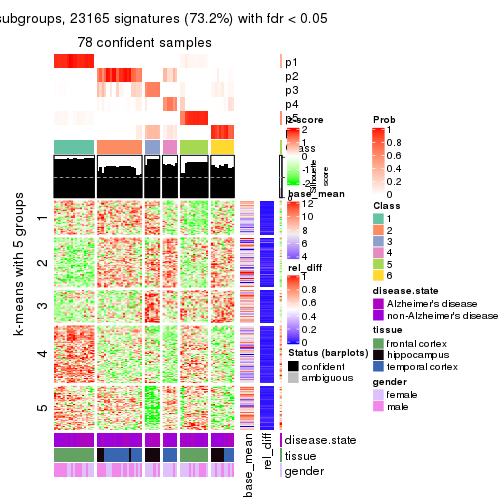
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
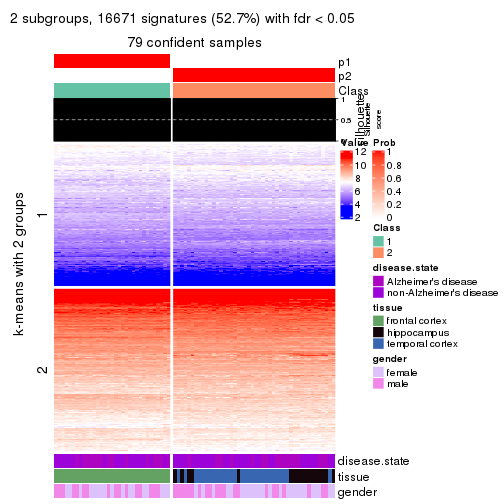
get_signatures(res, k = 3, scale_rows = FALSE)
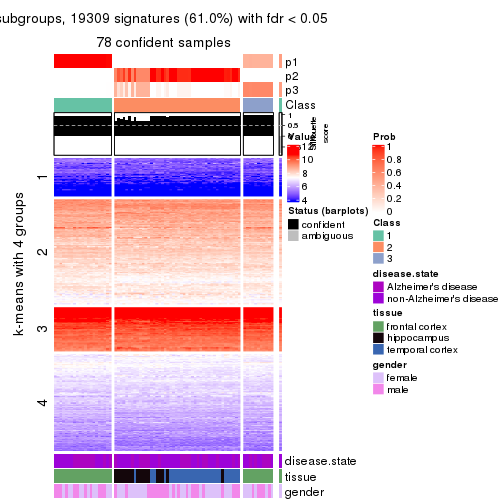
get_signatures(res, k = 4, scale_rows = FALSE)
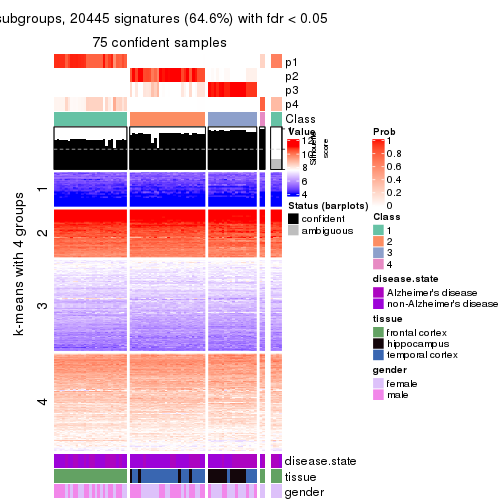
get_signatures(res, k = 5, scale_rows = FALSE)
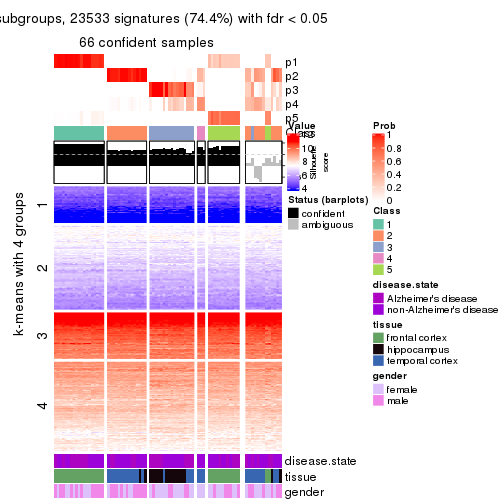
get_signatures(res, k = 6, scale_rows = FALSE)
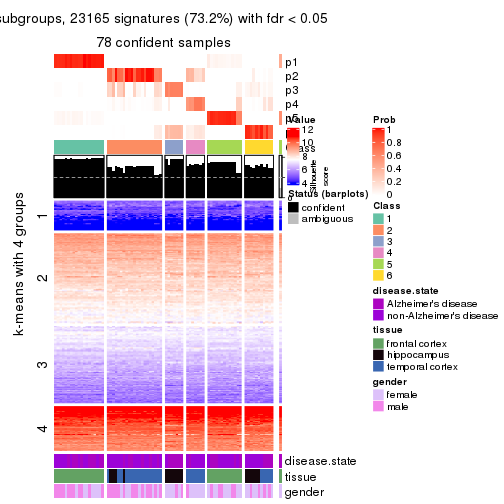
Compare the overlap of signatures from different k:
compare_signatures(res)
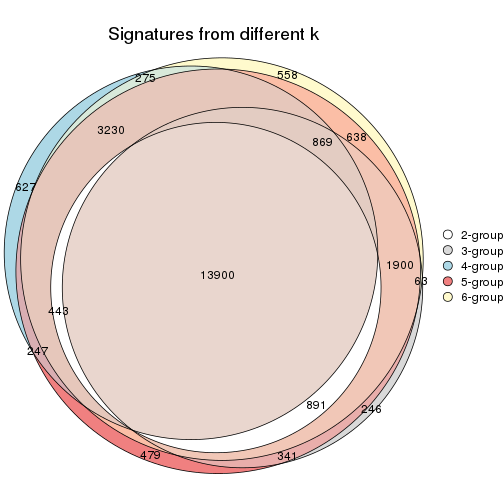
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
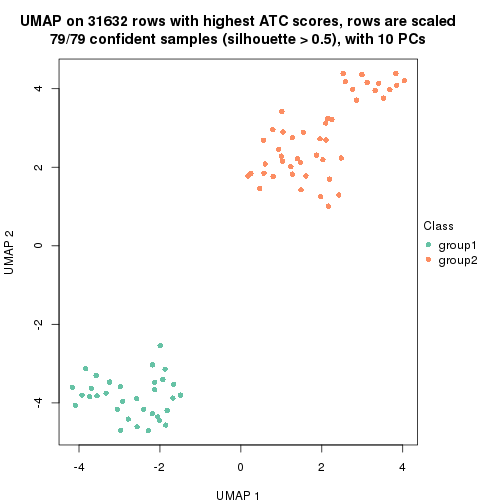
dimension_reduction(res, k = 3, method = "UMAP")
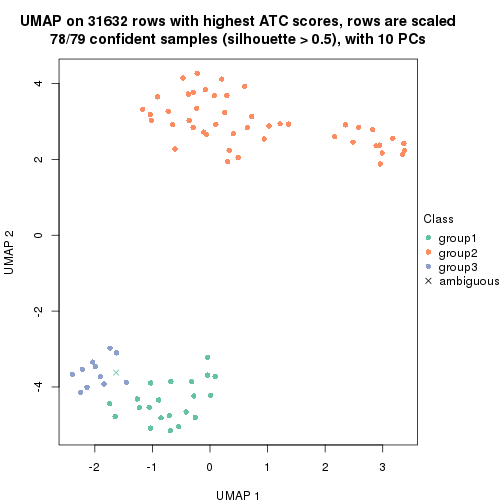
dimension_reduction(res, k = 4, method = "UMAP")
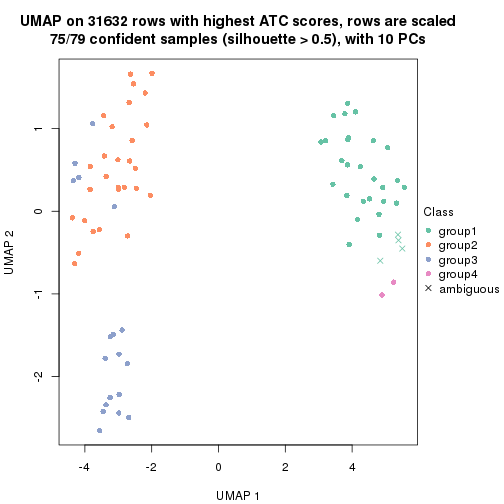
dimension_reduction(res, k = 5, method = "UMAP")
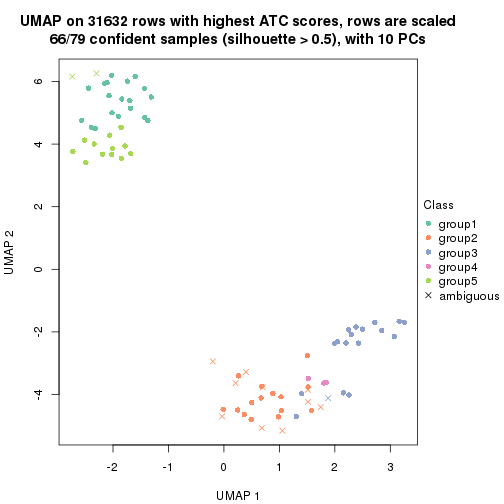
dimension_reduction(res, k = 6, method = "UMAP")
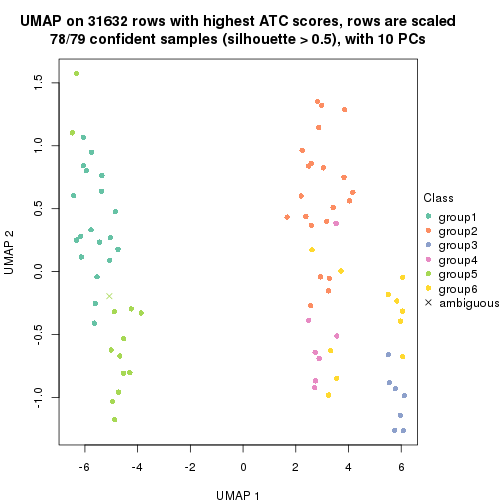
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
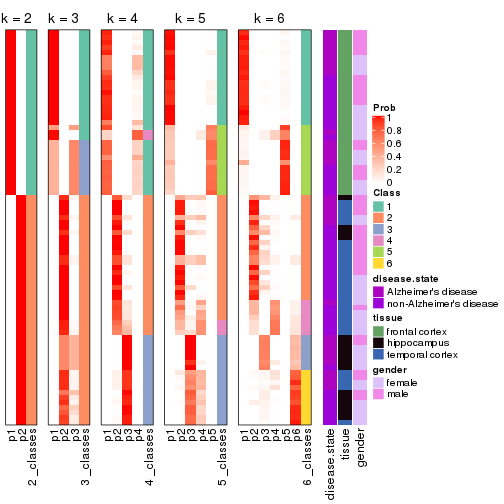
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:mclust 79 0.5986 7.00e-18 0.9838 2
#> ATC:mclust 78 0.6766 4.62e-16 0.8685 3
#> ATC:mclust 75 0.2099 1.76e-19 0.1677 4
#> ATC:mclust 66 0.3212 4.27e-17 0.0865 5
#> ATC:mclust 78 0.0846 1.61e-19 0.1093 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
The object with results only for a single top-value method and a single partition method can be extracted as:
res = res_list["ATC", "NMF"]
# you can also extract it by
# res = res_list["ATC:NMF"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4, 5, 6.
#> On a matrix with 31632 rows and 79 columns.
#> Top rows (1000, 2000, 3000, 4000, 5000) are extracted by 'ATC' method.
#> Subgroups are detected by 'NMF' method.
#> Performed in total 1250 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_signatures"
#> [7] "consensus_heatmap" "dimension_reduction" "functional_enrichment"
#> [10] "get_anno_col" "get_anno" "get_classes"
#> [13] "get_consensus" "get_matrix" "get_membership"
#> [16] "get_param" "get_signatures" "get_stats"
#> [19] "is_best_k" "is_stable_k" "membership_heatmap"
#> [22] "ncol" "nrow" "plot_ecdf"
#> [25] "rownames" "select_partition_number" "show"
#> [28] "suggest_best_k" "test_to_known_factors"
collect_plots() function collects all the plots made from res for all k (number of partitions)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
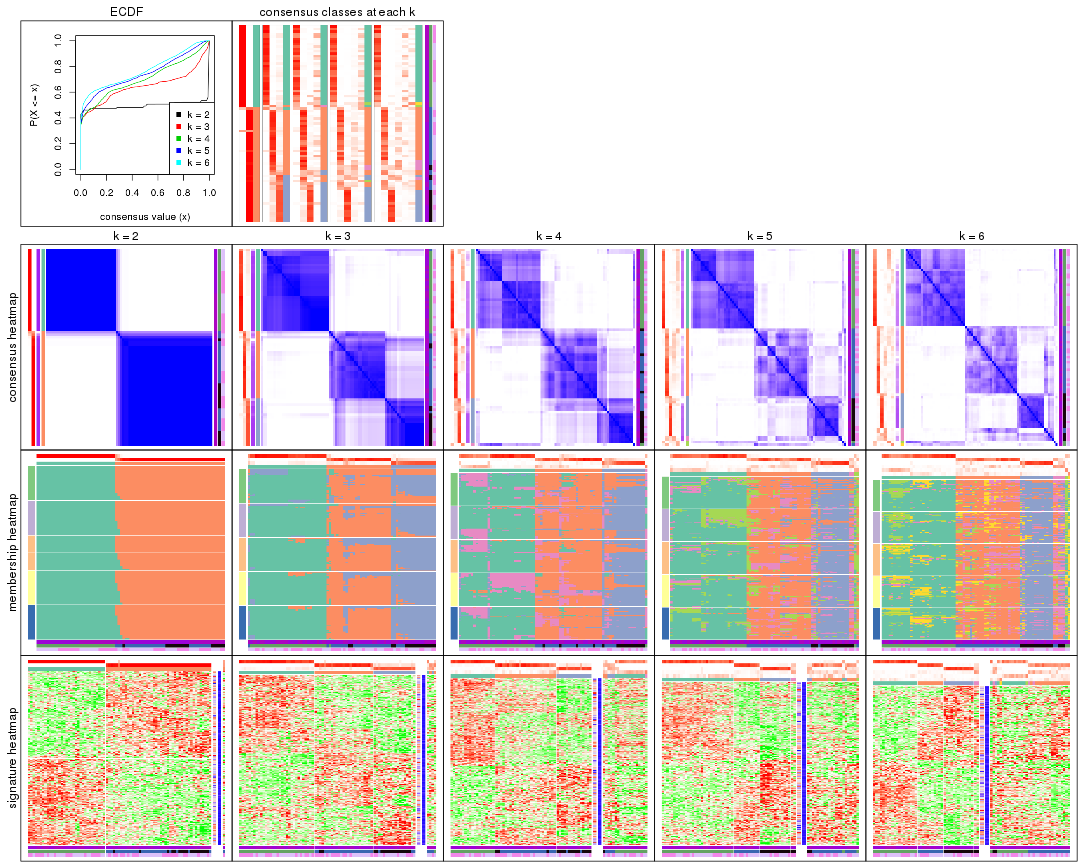
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, lower PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
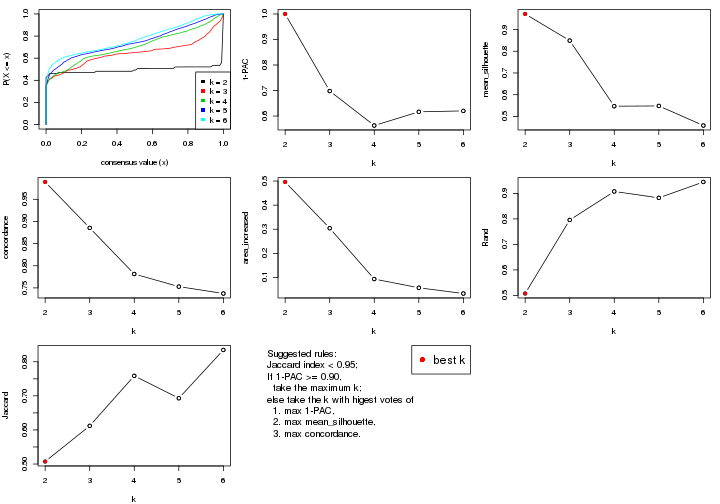
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.972 0.989 0.4962 0.507 0.507
#> 3 3 0.698 0.849 0.885 0.3043 0.796 0.612
#> 4 4 0.563 0.547 0.781 0.0933 0.907 0.759
#> 5 5 0.617 0.548 0.753 0.0571 0.883 0.693
#> 6 6 0.620 0.458 0.737 0.0333 0.945 0.835
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following shows the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall class
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> GSM907858 2 0.0000 0.981 0.000 1.000
#> GSM907859 2 0.0672 0.974 0.008 0.992
#> GSM907860 2 0.0000 0.981 0.000 1.000
#> GSM907854 2 0.0000 0.981 0.000 1.000
#> GSM907855 2 0.0000 0.981 0.000 1.000
#> GSM907856 2 0.0000 0.981 0.000 1.000
#> GSM907857 2 0.0000 0.981 0.000 1.000
#> GSM907825 2 0.0000 0.981 0.000 1.000
#> GSM907828 2 0.0000 0.981 0.000 1.000
#> GSM907832 2 0.0000 0.981 0.000 1.000
#> GSM907833 2 0.0000 0.981 0.000 1.000
#> GSM907834 2 0.0000 0.981 0.000 1.000
#> GSM907826 2 0.0000 0.981 0.000 1.000
#> GSM907827 2 0.0000 0.981 0.000 1.000
#> GSM907829 2 0.8555 0.617 0.280 0.720
#> GSM907830 2 0.0000 0.981 0.000 1.000
#> GSM907831 2 0.0000 0.981 0.000 1.000
#> GSM907792 1 0.0000 1.000 1.000 0.000
#> GSM907795 1 0.0000 1.000 1.000 0.000
#> GSM907801 1 0.0000 1.000 1.000 0.000
#> GSM907802 1 0.0000 1.000 1.000 0.000
#> GSM907804 1 0.0000 1.000 1.000 0.000
#> GSM907805 1 0.0000 1.000 1.000 0.000
#> GSM907806 1 0.0000 1.000 1.000 0.000
#> GSM907793 1 0.0000 1.000 1.000 0.000
#> GSM907794 1 0.0000 1.000 1.000 0.000
#> GSM907796 1 0.0000 1.000 1.000 0.000
#> GSM907797 1 0.0000 1.000 1.000 0.000
#> GSM907798 1 0.0000 1.000 1.000 0.000
#> GSM907799 1 0.0000 1.000 1.000 0.000
#> GSM907800 1 0.0000 1.000 1.000 0.000
#> GSM907803 1 0.0000 1.000 1.000 0.000
#> GSM907864 2 0.0000 0.981 0.000 1.000
#> GSM907865 2 0.0000 0.981 0.000 1.000
#> GSM907868 2 0.0000 0.981 0.000 1.000
#> GSM907869 2 0.0000 0.981 0.000 1.000
#> GSM907870 2 0.0000 0.981 0.000 1.000
#> GSM907861 2 0.0000 0.981 0.000 1.000
#> GSM907862 2 0.0000 0.981 0.000 1.000
#> GSM907863 2 0.0000 0.981 0.000 1.000
#> GSM907866 2 0.0000 0.981 0.000 1.000
#> GSM907867 2 0.0000 0.981 0.000 1.000
#> GSM907839 2 0.0000 0.981 0.000 1.000
#> GSM907840 2 0.0000 0.981 0.000 1.000
#> GSM907842 2 0.0000 0.981 0.000 1.000
#> GSM907843 2 0.0000 0.981 0.000 1.000
#> GSM907845 2 0.0938 0.971 0.012 0.988
#> GSM907846 2 0.9996 0.073 0.488 0.512
#> GSM907848 2 0.0000 0.981 0.000 1.000
#> GSM907851 2 0.0938 0.971 0.012 0.988
#> GSM907835 2 0.0000 0.981 0.000 1.000
#> GSM907836 2 0.0000 0.981 0.000 1.000
#> GSM907837 2 0.0000 0.981 0.000 1.000
#> GSM907838 2 0.0000 0.981 0.000 1.000
#> GSM907841 2 0.0000 0.981 0.000 1.000
#> GSM907844 2 0.0000 0.981 0.000 1.000
#> GSM907847 2 0.0000 0.981 0.000 1.000
#> GSM907849 2 0.3431 0.920 0.064 0.936
#> GSM907850 2 0.0000 0.981 0.000 1.000
#> GSM907852 2 0.0000 0.981 0.000 1.000
#> GSM907853 2 0.0000 0.981 0.000 1.000
#> GSM907807 1 0.0000 1.000 1.000 0.000
#> GSM907813 1 0.0000 1.000 1.000 0.000
#> GSM907814 1 0.0000 1.000 1.000 0.000
#> GSM907816 1 0.0000 1.000 1.000 0.000
#> GSM907818 1 0.0000 1.000 1.000 0.000
#> GSM907819 1 0.0000 1.000 1.000 0.000
#> GSM907820 1 0.0000 1.000 1.000 0.000
#> GSM907822 1 0.0000 1.000 1.000 0.000
#> GSM907823 1 0.0000 1.000 1.000 0.000
#> GSM907808 1 0.0000 1.000 1.000 0.000
#> GSM907809 1 0.0000 1.000 1.000 0.000
#> GSM907810 1 0.0000 1.000 1.000 0.000
#> GSM907811 1 0.0000 1.000 1.000 0.000
#> GSM907812 1 0.0000 1.000 1.000 0.000
#> GSM907815 1 0.0000 1.000 1.000 0.000
#> GSM907817 1 0.0000 1.000 1.000 0.000
#> GSM907821 1 0.0000 1.000 1.000 0.000
#> GSM907824 1 0.0000 1.000 1.000 0.000
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> GSM907858 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907859 3 0.4799 0.891 0.032 0.132 0.836
#> GSM907860 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907854 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907855 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907856 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907857 3 0.4830 0.806 0.084 0.068 0.848
#> GSM907825 2 0.5497 0.502 0.000 0.708 0.292
#> GSM907828 2 0.4121 0.749 0.000 0.832 0.168
#> GSM907832 2 0.1753 0.859 0.000 0.952 0.048
#> GSM907833 2 0.1643 0.859 0.000 0.956 0.044
#> GSM907834 3 0.6260 0.447 0.000 0.448 0.552
#> GSM907826 2 0.1289 0.858 0.000 0.968 0.032
#> GSM907827 3 0.5016 0.881 0.000 0.240 0.760
#> GSM907829 1 0.8223 0.364 0.604 0.108 0.288
#> GSM907830 2 0.1163 0.847 0.000 0.972 0.028
#> GSM907831 2 0.6267 -0.124 0.000 0.548 0.452
#> GSM907792 1 0.0592 0.939 0.988 0.000 0.012
#> GSM907795 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907801 1 0.0000 0.940 1.000 0.000 0.000
#> GSM907802 1 0.3918 0.908 0.868 0.012 0.120
#> GSM907804 1 0.4280 0.901 0.856 0.020 0.124
#> GSM907805 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907806 1 0.1643 0.939 0.956 0.000 0.044
#> GSM907793 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907794 1 0.1753 0.938 0.952 0.000 0.048
#> GSM907796 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907797 1 0.3412 0.864 0.876 0.000 0.124
#> GSM907798 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907799 1 0.0747 0.939 0.984 0.000 0.016
#> GSM907800 1 0.2066 0.937 0.940 0.000 0.060
#> GSM907803 1 0.1753 0.938 0.952 0.000 0.048
#> GSM907864 2 0.4750 0.675 0.000 0.784 0.216
#> GSM907865 3 0.4887 0.893 0.000 0.228 0.772
#> GSM907868 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907869 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907870 2 0.3619 0.790 0.000 0.864 0.136
#> GSM907861 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907862 3 0.4654 0.909 0.000 0.208 0.792
#> GSM907863 3 0.4399 0.922 0.000 0.188 0.812
#> GSM907866 3 0.4062 0.930 0.000 0.164 0.836
#> GSM907867 3 0.4346 0.924 0.000 0.184 0.816
#> GSM907839 2 0.1753 0.822 0.000 0.952 0.048
#> GSM907840 2 0.1643 0.859 0.000 0.956 0.044
#> GSM907842 2 0.1643 0.859 0.000 0.956 0.044
#> GSM907843 2 0.2774 0.796 0.008 0.920 0.072
#> GSM907845 3 0.6872 0.802 0.044 0.276 0.680
#> GSM907846 2 0.5111 0.701 0.036 0.820 0.144
#> GSM907848 2 0.2625 0.839 0.000 0.916 0.084
#> GSM907851 2 0.3445 0.783 0.016 0.896 0.088
#> GSM907835 2 0.1860 0.857 0.000 0.948 0.052
#> GSM907836 2 0.0892 0.856 0.000 0.980 0.020
#> GSM907837 2 0.1860 0.857 0.000 0.948 0.052
#> GSM907838 2 0.1964 0.856 0.000 0.944 0.056
#> GSM907841 3 0.5327 0.840 0.000 0.272 0.728
#> GSM907844 2 0.2165 0.852 0.000 0.936 0.064
#> GSM907847 2 0.1753 0.822 0.000 0.952 0.048
#> GSM907849 2 0.7595 0.597 0.176 0.688 0.136
#> GSM907850 2 0.2537 0.842 0.000 0.920 0.080
#> GSM907852 2 0.0747 0.845 0.000 0.984 0.016
#> GSM907853 2 0.1411 0.859 0.000 0.964 0.036
#> GSM907807 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907813 1 0.3618 0.916 0.884 0.012 0.104
#> GSM907814 1 0.0424 0.940 0.992 0.000 0.008
#> GSM907816 1 0.1753 0.938 0.952 0.000 0.048
#> GSM907818 1 0.2774 0.931 0.920 0.008 0.072
#> GSM907819 1 0.3454 0.919 0.888 0.008 0.104
#> GSM907820 1 0.4779 0.890 0.840 0.036 0.124
#> GSM907822 1 0.1989 0.938 0.948 0.004 0.048
#> GSM907823 1 0.2486 0.934 0.932 0.008 0.060
#> GSM907808 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907809 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907810 1 0.0592 0.939 0.988 0.000 0.012
#> GSM907811 1 0.3459 0.920 0.892 0.012 0.096
#> GSM907812 1 0.0892 0.938 0.980 0.000 0.020
#> GSM907815 1 0.3267 0.871 0.884 0.000 0.116
#> GSM907817 1 0.4413 0.899 0.852 0.024 0.124
#> GSM907821 1 0.1860 0.938 0.948 0.000 0.052
#> GSM907824 2 0.8408 0.444 0.244 0.612 0.144
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> GSM907858 3 0.2011 0.8204 0.000 0.080 0.920 0.000
#> GSM907859 2 0.9175 0.1160 0.116 0.372 0.152 0.360
#> GSM907860 3 0.2944 0.8328 0.000 0.128 0.868 0.004
#> GSM907854 3 0.2654 0.8331 0.000 0.108 0.888 0.004
#> GSM907855 3 0.2216 0.8281 0.000 0.092 0.908 0.000
#> GSM907856 3 0.2266 0.8220 0.000 0.084 0.912 0.004
#> GSM907857 3 0.5251 0.5148 0.028 0.008 0.712 0.252
#> GSM907825 3 0.7860 0.2599 0.000 0.340 0.384 0.276
#> GSM907828 2 0.2198 0.7673 0.000 0.920 0.072 0.008
#> GSM907832 2 0.0844 0.7698 0.012 0.980 0.004 0.004
#> GSM907833 2 0.2089 0.7746 0.000 0.932 0.048 0.020
#> GSM907834 3 0.6389 0.2931 0.000 0.448 0.488 0.064
#> GSM907826 2 0.4831 0.7012 0.000 0.752 0.040 0.208
#> GSM907827 3 0.4456 0.6987 0.000 0.280 0.716 0.004
#> GSM907829 2 0.8010 0.1712 0.312 0.432 0.008 0.248
#> GSM907830 2 0.2197 0.7743 0.000 0.928 0.048 0.024
#> GSM907831 3 0.7502 0.3692 0.000 0.356 0.456 0.188
#> GSM907792 1 0.0524 0.6496 0.988 0.000 0.004 0.008
#> GSM907795 1 0.3279 0.6011 0.872 0.032 0.000 0.096
#> GSM907801 1 0.1004 0.6518 0.972 0.024 0.000 0.004
#> GSM907802 1 0.5050 -0.1894 0.588 0.000 0.004 0.408
#> GSM907804 1 0.4933 -0.2744 0.568 0.000 0.000 0.432
#> GSM907805 1 0.2002 0.6441 0.936 0.020 0.000 0.044
#> GSM907806 1 0.0921 0.6428 0.972 0.000 0.000 0.028
#> GSM907793 1 0.2131 0.6418 0.932 0.000 0.032 0.036
#> GSM907794 1 0.4387 0.3720 0.752 0.000 0.012 0.236
#> GSM907796 1 0.2313 0.6394 0.924 0.000 0.032 0.044
#> GSM907797 1 0.7855 -0.1033 0.400 0.000 0.300 0.300
#> GSM907798 1 0.2715 0.6080 0.892 0.004 0.004 0.100
#> GSM907799 1 0.1629 0.6362 0.952 0.000 0.024 0.024
#> GSM907800 1 0.5174 -0.0805 0.620 0.000 0.012 0.368
#> GSM907803 1 0.4137 0.4266 0.780 0.000 0.012 0.208
#> GSM907864 2 0.1489 0.7757 0.000 0.952 0.044 0.004
#> GSM907865 2 0.3931 0.7088 0.000 0.832 0.128 0.040
#> GSM907868 3 0.2859 0.8337 0.000 0.112 0.880 0.008
#> GSM907869 3 0.2216 0.8282 0.000 0.092 0.908 0.000
#> GSM907870 2 0.4171 0.7371 0.000 0.828 0.088 0.084
#> GSM907861 3 0.3377 0.8296 0.000 0.140 0.848 0.012
#> GSM907862 3 0.3597 0.8236 0.000 0.148 0.836 0.016
#> GSM907863 3 0.3157 0.8289 0.000 0.144 0.852 0.004
#> GSM907866 3 0.2593 0.8322 0.000 0.104 0.892 0.004
#> GSM907867 3 0.3105 0.8300 0.000 0.140 0.856 0.004
#> GSM907839 2 0.0376 0.7735 0.004 0.992 0.004 0.000
#> GSM907840 2 0.4590 0.7254 0.000 0.792 0.060 0.148
#> GSM907842 2 0.1118 0.7751 0.000 0.964 0.036 0.000
#> GSM907843 2 0.2782 0.7337 0.068 0.904 0.004 0.024
#> GSM907845 2 0.6808 0.5097 0.164 0.620 0.004 0.212
#> GSM907846 2 0.3668 0.6969 0.116 0.852 0.004 0.028
#> GSM907848 2 0.1474 0.7727 0.000 0.948 0.052 0.000
#> GSM907851 2 0.4090 0.6886 0.116 0.836 0.008 0.040
#> GSM907835 2 0.4636 0.7242 0.000 0.792 0.068 0.140
#> GSM907836 2 0.3239 0.7652 0.000 0.880 0.052 0.068
#> GSM907837 2 0.5814 0.5927 0.000 0.644 0.056 0.300
#> GSM907838 2 0.6627 0.5105 0.000 0.588 0.112 0.300
#> GSM907841 3 0.4964 0.5365 0.000 0.380 0.616 0.004
#> GSM907844 2 0.4735 0.7195 0.000 0.784 0.068 0.148
#> GSM907847 2 0.1082 0.7672 0.020 0.972 0.004 0.004
#> GSM907849 2 0.5843 0.5969 0.156 0.716 0.004 0.124
#> GSM907850 2 0.1389 0.7738 0.000 0.952 0.048 0.000
#> GSM907852 2 0.5550 0.5202 0.000 0.552 0.020 0.428
#> GSM907853 2 0.3392 0.7619 0.000 0.872 0.056 0.072
#> GSM907807 1 0.0804 0.6501 0.980 0.000 0.008 0.012
#> GSM907813 1 0.3436 0.5808 0.864 0.016 0.008 0.112
#> GSM907814 1 0.3009 0.6211 0.892 0.056 0.000 0.052
#> GSM907816 1 0.1936 0.6450 0.940 0.032 0.000 0.028
#> GSM907818 1 0.4800 0.0908 0.656 0.000 0.004 0.340
#> GSM907819 1 0.4836 0.1544 0.672 0.000 0.008 0.320
#> GSM907820 1 0.5155 -0.4657 0.528 0.000 0.004 0.468
#> GSM907822 1 0.1452 0.6485 0.956 0.036 0.000 0.008
#> GSM907823 1 0.1576 0.6437 0.948 0.048 0.000 0.004
#> GSM907808 1 0.2908 0.6246 0.896 0.040 0.000 0.064
#> GSM907809 1 0.3308 0.6025 0.872 0.036 0.000 0.092
#> GSM907810 1 0.1833 0.6470 0.944 0.032 0.000 0.024
#> GSM907811 1 0.5080 -0.2551 0.576 0.000 0.004 0.420
#> GSM907812 1 0.2125 0.6422 0.932 0.012 0.004 0.052
#> GSM907815 1 0.5764 0.1974 0.644 0.000 0.304 0.052
#> GSM907817 1 0.4941 -0.2943 0.564 0.000 0.000 0.436
#> GSM907821 1 0.4428 0.2905 0.720 0.000 0.004 0.276
#> GSM907824 4 0.5286 0.0000 0.384 0.004 0.008 0.604
cbind(get_classes(res, k = 5), get_membership(res, k = 5))
#> class entropy silhouette p1 p2 p3 p4 p5
#> GSM907858 3 0.1997 0.7622 0.000 0.024 0.932 0.016 0.028
#> GSM907859 3 0.8474 -0.2232 0.016 0.172 0.420 0.236 0.156
#> GSM907860 3 0.1041 0.7658 0.000 0.032 0.964 0.004 0.000
#> GSM907854 3 0.1673 0.7648 0.000 0.032 0.944 0.016 0.008
#> GSM907855 3 0.2072 0.7526 0.000 0.020 0.928 0.036 0.016
#> GSM907856 3 0.2249 0.7481 0.000 0.020 0.920 0.040 0.020
#> GSM907857 3 0.5335 0.5736 0.020 0.004 0.716 0.092 0.168
#> GSM907825 2 0.7103 0.3801 0.000 0.520 0.144 0.276 0.060
#> GSM907828 2 0.2270 0.5802 0.000 0.916 0.052 0.020 0.012
#> GSM907832 2 0.3605 0.5352 0.024 0.848 0.000 0.056 0.072
#> GSM907833 2 0.2095 0.5449 0.000 0.920 0.012 0.060 0.008
#> GSM907834 2 0.6490 0.4296 0.000 0.600 0.164 0.200 0.036
#> GSM907826 2 0.3808 0.5653 0.000 0.840 0.060 0.060 0.040
#> GSM907827 2 0.7293 0.3171 0.000 0.484 0.208 0.260 0.048
#> GSM907829 2 0.7042 -0.2321 0.084 0.436 0.004 0.064 0.412
#> GSM907830 2 0.1522 0.5781 0.000 0.944 0.044 0.012 0.000
#> GSM907831 2 0.7114 0.3659 0.000 0.512 0.160 0.276 0.052
#> GSM907792 1 0.0324 0.7791 0.992 0.000 0.000 0.004 0.004
#> GSM907795 1 0.4391 0.5729 0.744 0.016 0.000 0.024 0.216
#> GSM907801 1 0.1200 0.7773 0.964 0.008 0.000 0.012 0.016
#> GSM907802 1 0.4311 0.7182 0.712 0.000 0.004 0.020 0.264
#> GSM907804 1 0.4288 0.6804 0.664 0.000 0.000 0.012 0.324
#> GSM907805 1 0.2270 0.7498 0.908 0.004 0.000 0.016 0.072
#> GSM907806 1 0.1364 0.7837 0.952 0.000 0.000 0.012 0.036
#> GSM907793 1 0.2407 0.7501 0.896 0.000 0.004 0.012 0.088
#> GSM907794 1 0.3274 0.7518 0.780 0.000 0.000 0.000 0.220
#> GSM907796 1 0.2568 0.7425 0.888 0.000 0.004 0.016 0.092
#> GSM907797 5 0.7769 0.0789 0.344 0.000 0.128 0.120 0.408
#> GSM907798 1 0.3759 0.5835 0.764 0.000 0.000 0.016 0.220
#> GSM907799 1 0.0833 0.7798 0.976 0.000 0.004 0.016 0.004
#> GSM907800 1 0.4403 0.7256 0.724 0.000 0.004 0.032 0.240
#> GSM907803 1 0.3328 0.7634 0.812 0.000 0.004 0.008 0.176
#> GSM907864 4 0.6558 0.8643 0.000 0.300 0.232 0.468 0.000
#> GSM907865 3 0.6911 -0.3913 0.000 0.172 0.424 0.384 0.020
#> GSM907868 3 0.2104 0.7555 0.000 0.060 0.916 0.024 0.000
#> GSM907869 3 0.2086 0.7615 0.000 0.028 0.928 0.028 0.016
#> GSM907870 4 0.7525 0.8544 0.000 0.336 0.184 0.420 0.060
#> GSM907861 3 0.3997 0.7131 0.000 0.092 0.820 0.068 0.020
#> GSM907862 3 0.3471 0.7143 0.000 0.092 0.836 0.072 0.000
#> GSM907863 3 0.3805 0.7013 0.000 0.092 0.820 0.084 0.004
#> GSM907866 3 0.1978 0.7575 0.000 0.024 0.932 0.032 0.012
#> GSM907867 3 0.3577 0.7186 0.000 0.084 0.836 0.076 0.004
#> GSM907839 2 0.5234 0.0565 0.004 0.612 0.000 0.332 0.052
#> GSM907840 2 0.4992 0.0810 0.000 0.640 0.028 0.320 0.012
#> GSM907842 2 0.3803 0.4453 0.004 0.812 0.004 0.144 0.036
#> GSM907843 2 0.6480 0.1456 0.040 0.584 0.000 0.260 0.116
#> GSM907845 5 0.6947 -0.2194 0.080 0.404 0.000 0.072 0.444
#> GSM907846 2 0.6668 0.2131 0.052 0.584 0.008 0.268 0.088
#> GSM907848 2 0.2180 0.5592 0.000 0.924 0.024 0.032 0.020
#> GSM907851 2 0.6839 0.0948 0.056 0.548 0.000 0.276 0.120
#> GSM907835 2 0.3649 0.5676 0.000 0.848 0.064 0.056 0.032
#> GSM907836 2 0.3304 0.4582 0.000 0.816 0.016 0.168 0.000
#> GSM907837 2 0.5722 0.4764 0.000 0.700 0.068 0.152 0.080
#> GSM907838 2 0.5906 0.4559 0.000 0.684 0.064 0.156 0.096
#> GSM907841 3 0.5192 0.1233 0.000 0.388 0.572 0.032 0.008
#> GSM907844 2 0.4411 0.5587 0.000 0.796 0.068 0.104 0.032
#> GSM907847 2 0.4545 0.3527 0.008 0.740 0.000 0.204 0.048
#> GSM907849 2 0.7670 -0.2273 0.100 0.412 0.000 0.136 0.352
#> GSM907850 2 0.2812 0.5051 0.000 0.876 0.004 0.096 0.024
#> GSM907852 2 0.5732 0.5022 0.000 0.684 0.036 0.172 0.108
#> GSM907853 2 0.2568 0.5804 0.000 0.904 0.048 0.032 0.016
#> GSM907807 1 0.1329 0.7783 0.956 0.000 0.004 0.032 0.008
#> GSM907813 1 0.3916 0.7578 0.780 0.000 0.004 0.028 0.188
#> GSM907814 1 0.3326 0.7342 0.860 0.016 0.000 0.044 0.080
#> GSM907816 1 0.1862 0.7841 0.932 0.004 0.000 0.016 0.048
#> GSM907818 1 0.3534 0.7347 0.744 0.000 0.000 0.000 0.256
#> GSM907819 1 0.3817 0.7348 0.740 0.000 0.004 0.004 0.252
#> GSM907820 1 0.4348 0.6824 0.668 0.000 0.000 0.016 0.316
#> GSM907822 1 0.1989 0.7789 0.932 0.016 0.000 0.020 0.032
#> GSM907823 1 0.2494 0.7755 0.908 0.016 0.000 0.032 0.044
#> GSM907808 1 0.3427 0.7179 0.848 0.016 0.000 0.032 0.104
#> GSM907809 1 0.4110 0.6625 0.792 0.012 0.000 0.044 0.152
#> GSM907810 1 0.2027 0.7648 0.928 0.008 0.000 0.024 0.040
#> GSM907811 1 0.4183 0.6834 0.668 0.000 0.000 0.008 0.324
#> GSM907812 1 0.2784 0.7235 0.872 0.004 0.000 0.016 0.108
#> GSM907815 1 0.5831 0.5935 0.700 0.000 0.108 0.108 0.084
#> GSM907817 1 0.4251 0.6874 0.672 0.000 0.000 0.012 0.316
#> GSM907821 1 0.3509 0.7571 0.792 0.000 0.004 0.008 0.196
#> GSM907824 1 0.6966 0.3371 0.460 0.040 0.000 0.132 0.368
cbind(get_classes(res, k = 6), get_membership(res, k = 6))
#> class entropy silhouette p1 p2 p3 p4 p5 p6
#> GSM907858 3 0.2165 0.83991 0.000 0.004 0.912 0.024 0.008 0.052
#> GSM907859 3 0.6751 0.06658 0.008 0.080 0.496 0.328 0.016 0.072
#> GSM907860 3 0.2986 0.82074 0.000 0.048 0.876 0.032 0.012 0.032
#> GSM907854 3 0.1364 0.85089 0.000 0.020 0.952 0.000 0.016 0.012
#> GSM907855 3 0.1452 0.84753 0.000 0.012 0.948 0.000 0.020 0.020
#> GSM907856 3 0.2100 0.83686 0.000 0.008 0.916 0.004 0.024 0.048
#> GSM907857 3 0.4771 0.62797 0.004 0.000 0.684 0.040 0.028 0.244
#> GSM907825 2 0.6457 0.47317 0.000 0.596 0.064 0.024 0.156 0.160
#> GSM907828 2 0.2289 0.59828 0.000 0.912 0.036 0.020 0.008 0.024
#> GSM907832 2 0.3269 0.53704 0.000 0.832 0.000 0.108 0.008 0.052
#> GSM907833 2 0.2798 0.55553 0.000 0.860 0.000 0.108 0.012 0.020
#> GSM907834 2 0.6298 0.48461 0.000 0.592 0.096 0.008 0.204 0.100
#> GSM907826 2 0.4108 0.58171 0.000 0.808 0.040 0.024 0.084 0.044
#> GSM907827 2 0.7081 0.35644 0.000 0.520 0.160 0.020 0.108 0.192
#> GSM907829 2 0.6337 0.38084 0.028 0.568 0.000 0.136 0.028 0.240
#> GSM907830 2 0.2832 0.57650 0.000 0.880 0.008 0.056 0.016 0.040
#> GSM907831 2 0.6336 0.48275 0.000 0.628 0.108 0.028 0.104 0.132
#> GSM907792 1 0.0837 0.65480 0.972 0.000 0.000 0.004 0.020 0.004
#> GSM907795 1 0.4573 0.45469 0.712 0.000 0.000 0.072 0.016 0.200
#> GSM907801 1 0.0653 0.65564 0.980 0.000 0.000 0.004 0.004 0.012
#> GSM907802 1 0.4887 -0.31910 0.536 0.000 0.000 0.008 0.412 0.044
#> GSM907804 1 0.4114 -0.33915 0.532 0.000 0.000 0.004 0.460 0.004
#> GSM907805 1 0.2013 0.64570 0.908 0.000 0.000 0.008 0.008 0.076
#> GSM907806 1 0.1686 0.64031 0.924 0.000 0.000 0.012 0.064 0.000
#> GSM907793 1 0.2565 0.63062 0.872 0.000 0.000 0.016 0.008 0.104
#> GSM907794 1 0.2955 0.54686 0.816 0.000 0.000 0.008 0.172 0.004
#> GSM907796 1 0.3268 0.58639 0.808 0.000 0.000 0.008 0.020 0.164
#> GSM907797 6 0.5874 0.00000 0.288 0.000 0.080 0.008 0.044 0.580
#> GSM907798 1 0.3610 0.51648 0.768 0.000 0.000 0.028 0.004 0.200
#> GSM907799 1 0.1434 0.65683 0.948 0.000 0.000 0.008 0.024 0.020
#> GSM907800 1 0.4433 0.06461 0.616 0.000 0.000 0.000 0.344 0.040
#> GSM907803 1 0.2655 0.58160 0.848 0.000 0.000 0.008 0.140 0.004
#> GSM907864 4 0.6436 0.54041 0.000 0.180 0.228 0.544 0.016 0.032
#> GSM907865 4 0.6284 0.14583 0.000 0.088 0.400 0.460 0.020 0.032
#> GSM907868 3 0.1736 0.84924 0.000 0.020 0.936 0.032 0.004 0.008
#> GSM907869 3 0.3082 0.82059 0.000 0.008 0.860 0.040 0.012 0.080
#> GSM907870 4 0.7550 0.50952 0.000 0.200 0.252 0.436 0.048 0.064
#> GSM907861 3 0.2401 0.83811 0.000 0.020 0.900 0.060 0.004 0.016
#> GSM907862 3 0.3458 0.79730 0.000 0.056 0.840 0.072 0.004 0.028
#> GSM907863 3 0.3561 0.80312 0.000 0.044 0.836 0.080 0.008 0.032
#> GSM907866 3 0.2109 0.84595 0.000 0.024 0.920 0.004 0.028 0.024
#> GSM907867 3 0.2226 0.83861 0.000 0.028 0.904 0.060 0.000 0.008
#> GSM907839 4 0.4456 0.09416 0.000 0.456 0.000 0.520 0.004 0.020
#> GSM907840 2 0.6366 0.14586 0.000 0.548 0.036 0.300 0.056 0.060
#> GSM907842 2 0.3621 0.46974 0.000 0.772 0.000 0.192 0.004 0.032
#> GSM907843 2 0.4802 -0.00475 0.000 0.540 0.000 0.404 0.000 0.056
#> GSM907845 2 0.5903 0.37423 0.012 0.600 0.000 0.160 0.020 0.208
#> GSM907846 2 0.5856 0.20707 0.024 0.556 0.000 0.328 0.020 0.072
#> GSM907848 2 0.2945 0.57881 0.000 0.868 0.000 0.064 0.040 0.028
#> GSM907851 4 0.5432 -0.00543 0.012 0.456 0.000 0.460 0.004 0.068
#> GSM907835 2 0.3669 0.58393 0.000 0.840 0.028 0.036 0.052 0.044
#> GSM907836 2 0.4065 0.39119 0.000 0.708 0.004 0.260 0.004 0.024
#> GSM907837 2 0.6746 0.42994 0.000 0.592 0.076 0.088 0.176 0.068
#> GSM907838 2 0.7143 0.35757 0.000 0.532 0.076 0.100 0.224 0.068
#> GSM907841 2 0.6904 0.19210 0.000 0.480 0.316 0.024 0.076 0.104
#> GSM907844 2 0.3964 0.58879 0.000 0.820 0.064 0.028 0.032 0.056
#> GSM907847 2 0.4395 0.34687 0.000 0.684 0.000 0.264 0.008 0.044
#> GSM907849 2 0.6088 0.20527 0.008 0.536 0.000 0.300 0.024 0.132
#> GSM907850 2 0.3105 0.53924 0.000 0.844 0.000 0.108 0.012 0.036
#> GSM907852 2 0.5169 0.54606 0.004 0.696 0.020 0.020 0.196 0.064
#> GSM907853 2 0.2059 0.59707 0.000 0.924 0.008 0.024 0.024 0.020
#> GSM907807 1 0.1003 0.65577 0.964 0.000 0.000 0.004 0.004 0.028
#> GSM907813 1 0.4022 0.49956 0.764 0.000 0.000 0.036 0.176 0.024
#> GSM907814 1 0.3710 0.58998 0.804 0.000 0.000 0.060 0.016 0.120
#> GSM907816 1 0.2206 0.63415 0.904 0.000 0.000 0.024 0.064 0.008
#> GSM907818 1 0.3915 0.33755 0.696 0.000 0.000 0.008 0.284 0.012
#> GSM907819 1 0.4103 0.25693 0.672 0.000 0.000 0.012 0.304 0.012
#> GSM907820 1 0.4716 -0.44375 0.504 0.008 0.000 0.016 0.464 0.008
#> GSM907822 1 0.1930 0.65106 0.924 0.000 0.000 0.028 0.036 0.012
#> GSM907823 1 0.2570 0.64672 0.892 0.000 0.000 0.032 0.040 0.036
#> GSM907808 1 0.3265 0.62027 0.828 0.000 0.000 0.056 0.004 0.112
#> GSM907809 1 0.3648 0.57332 0.788 0.000 0.000 0.028 0.016 0.168
#> GSM907810 1 0.1769 0.64896 0.924 0.000 0.000 0.012 0.004 0.060
#> GSM907811 1 0.4150 0.10254 0.616 0.000 0.000 0.008 0.368 0.008
#> GSM907812 1 0.2592 0.62160 0.864 0.000 0.000 0.016 0.004 0.116
#> GSM907815 1 0.5993 0.02498 0.596 0.000 0.080 0.012 0.056 0.256
#> GSM907817 1 0.4523 -0.20438 0.556 0.000 0.000 0.012 0.416 0.016
#> GSM907821 1 0.3622 0.44912 0.744 0.000 0.000 0.004 0.236 0.016
#> GSM907824 5 0.5325 0.00000 0.344 0.024 0.004 0.004 0.580 0.044
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
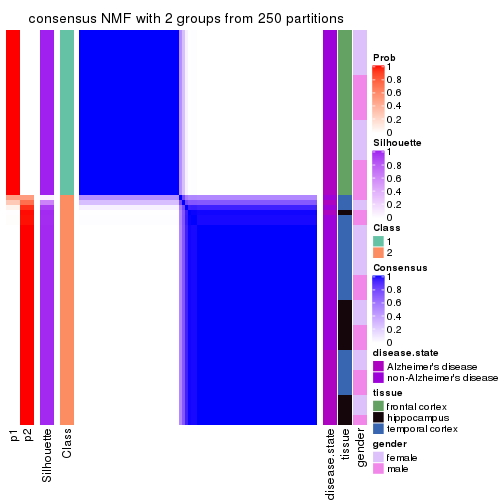
consensus_heatmap(res, k = 3)
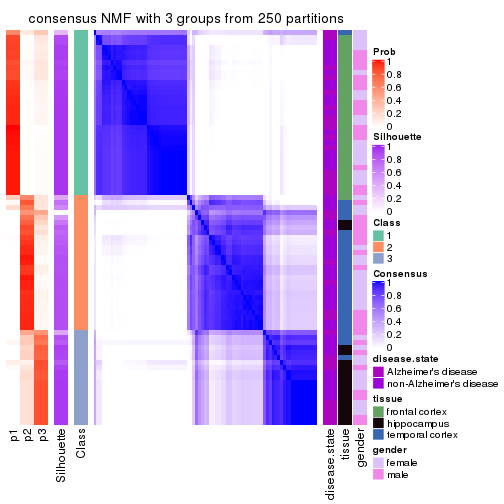
consensus_heatmap(res, k = 4)
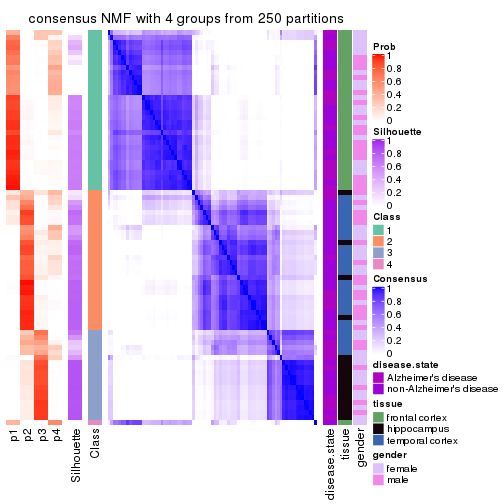
consensus_heatmap(res, k = 5)
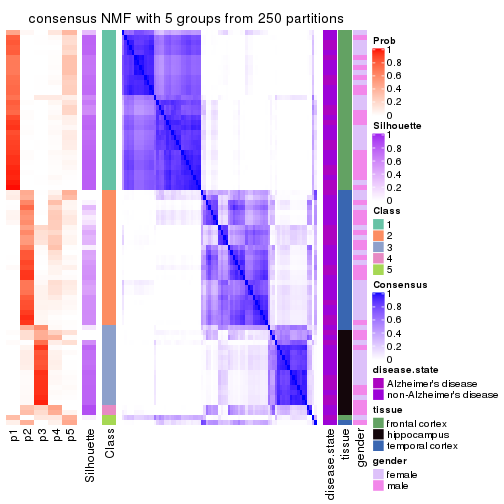
consensus_heatmap(res, k = 6)
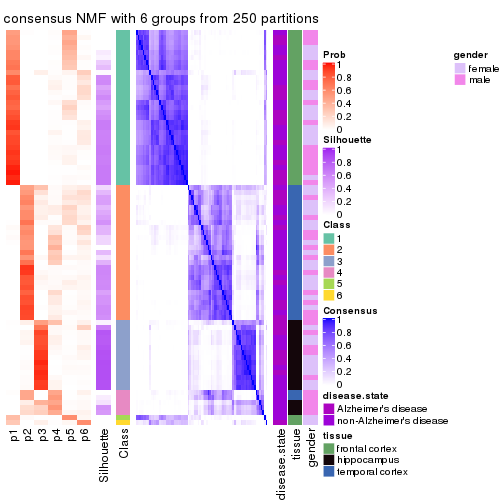
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
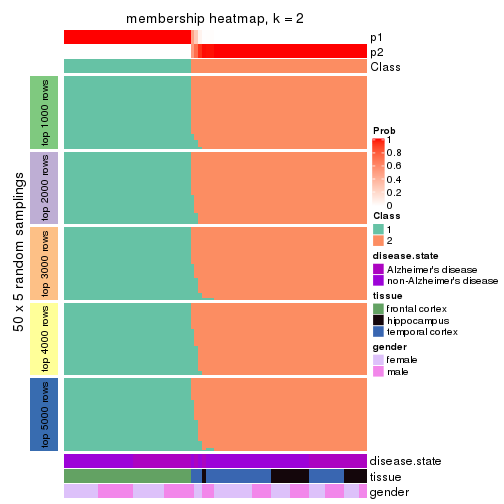
membership_heatmap(res, k = 3)
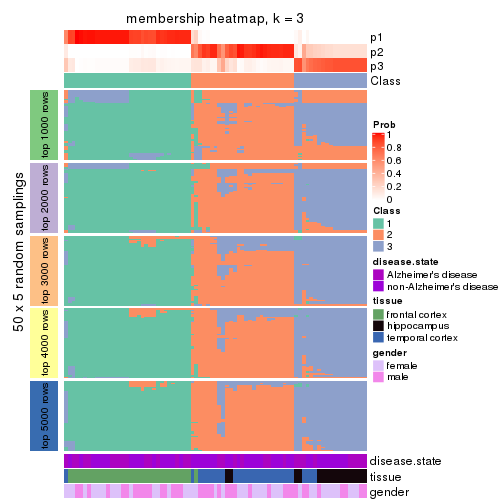
membership_heatmap(res, k = 4)
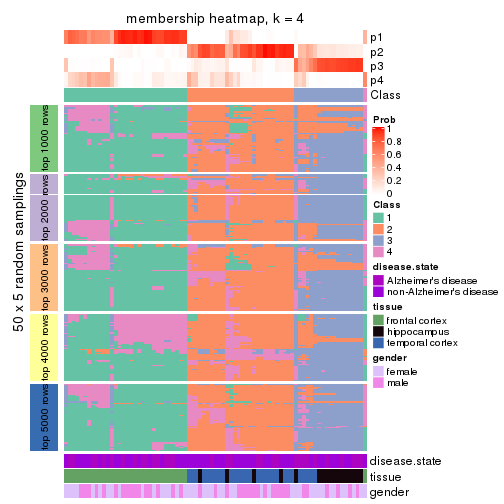
membership_heatmap(res, k = 5)
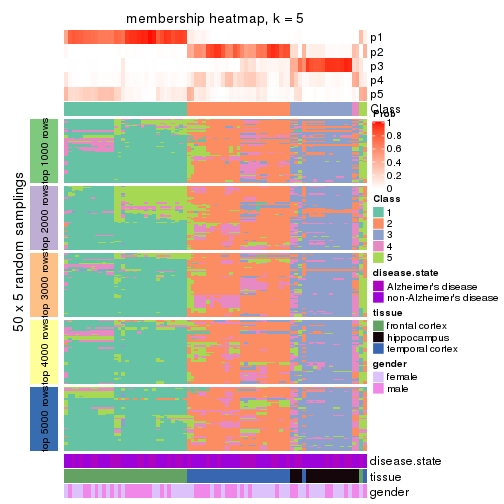
membership_heatmap(res, k = 6)
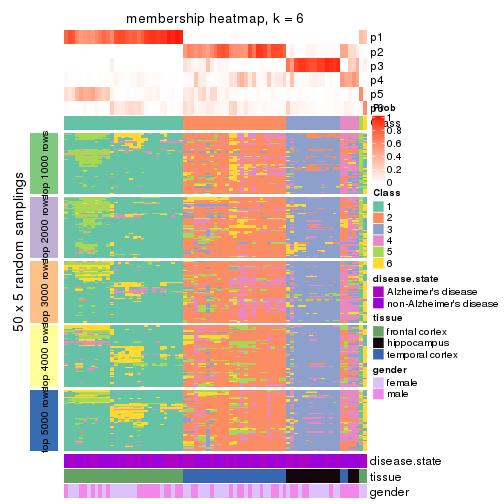
As soon as we have had the classes for columns, we can look for signatures which are significantly different between classes which can be candidate marks for certain classes. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
get_signatures(res, k = 2)
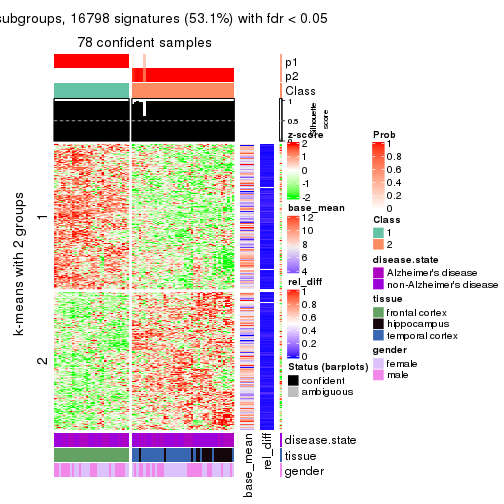
get_signatures(res, k = 3)
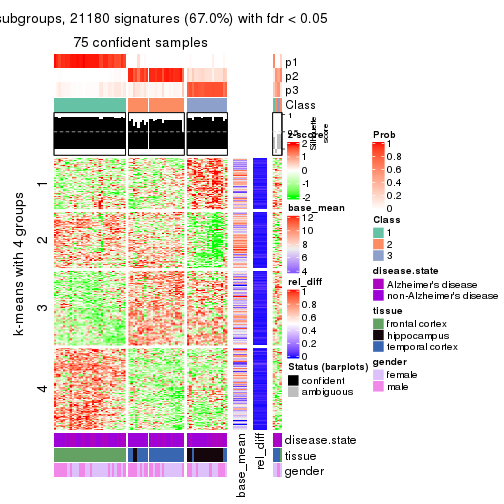
get_signatures(res, k = 4)
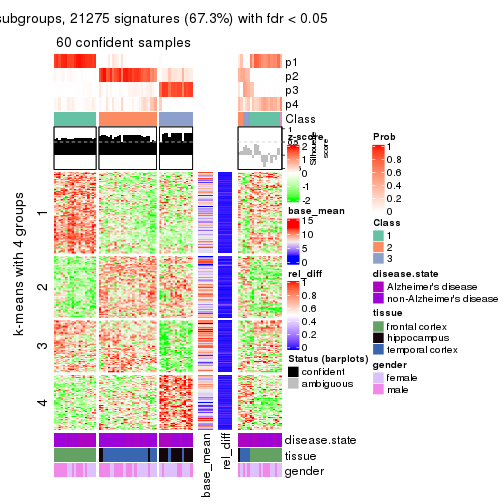
get_signatures(res, k = 5)
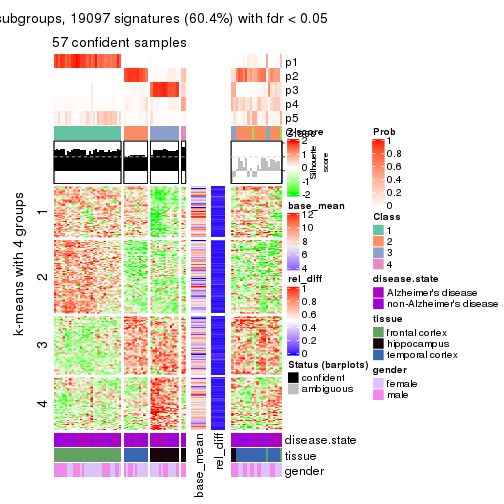
get_signatures(res, k = 6)
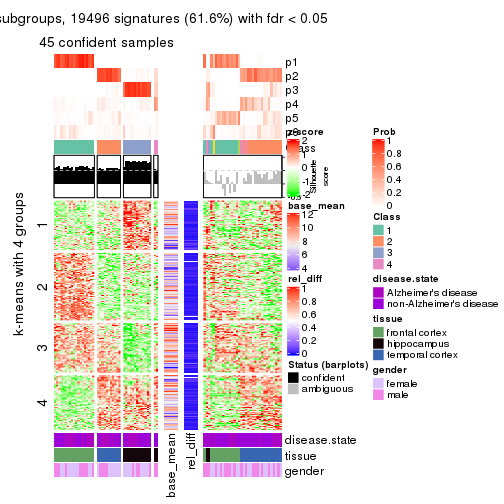
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
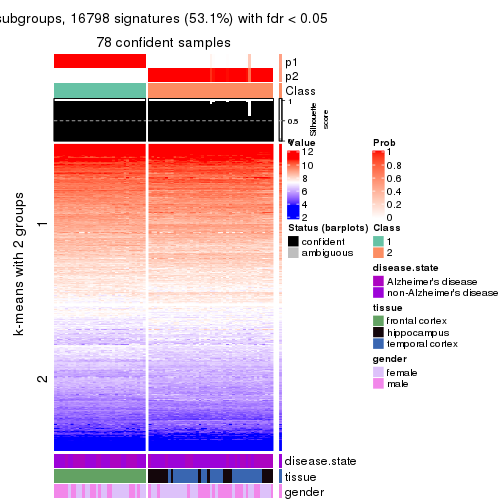
get_signatures(res, k = 3, scale_rows = FALSE)
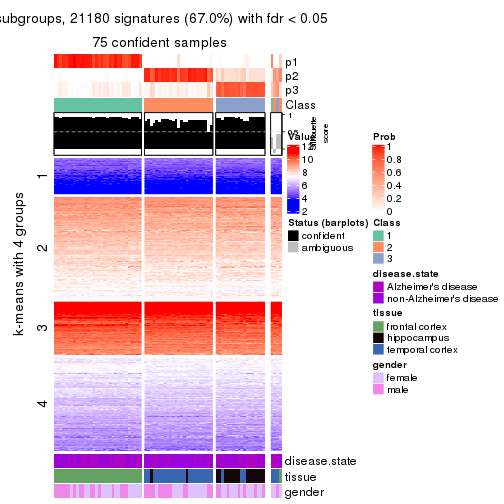
get_signatures(res, k = 4, scale_rows = FALSE)
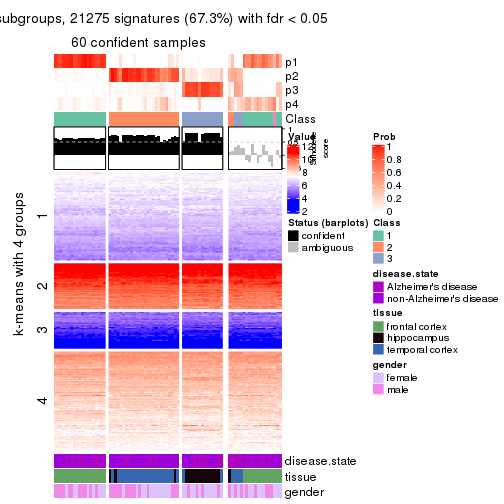
get_signatures(res, k = 5, scale_rows = FALSE)
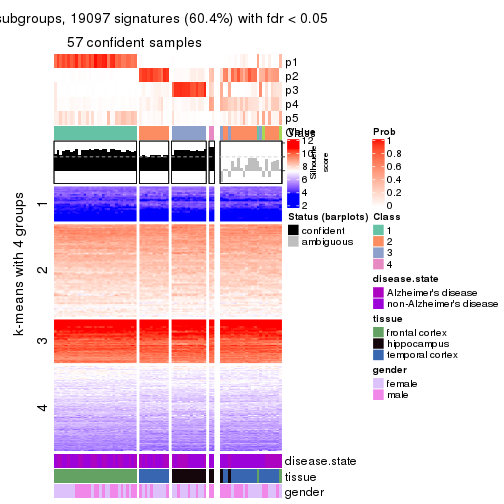
get_signatures(res, k = 6, scale_rows = FALSE)
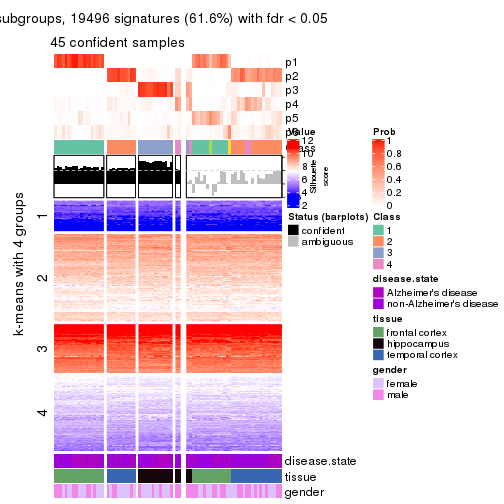
Compare the overlap of signatures from different k:
compare_signatures(res)
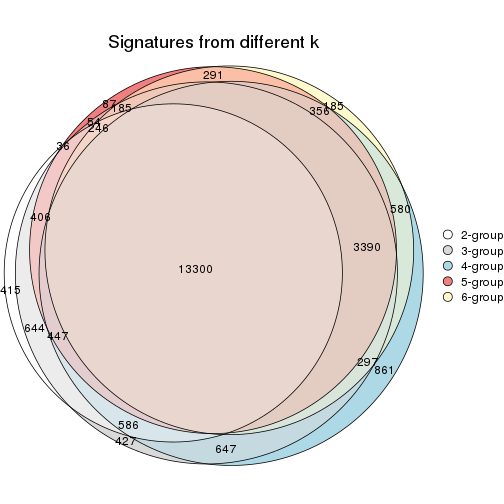
get_signature() returns a data frame invisibly. TO get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows.UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
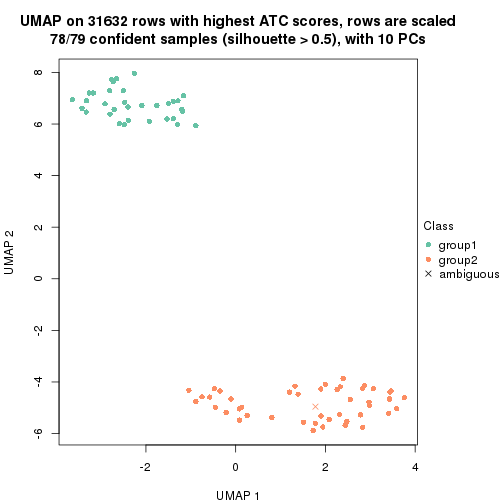
dimension_reduction(res, k = 3, method = "UMAP")
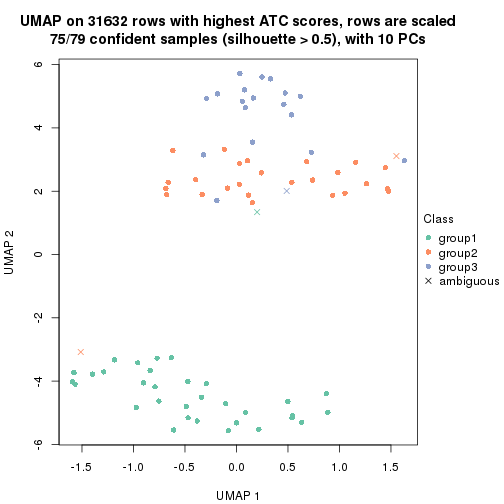
dimension_reduction(res, k = 4, method = "UMAP")
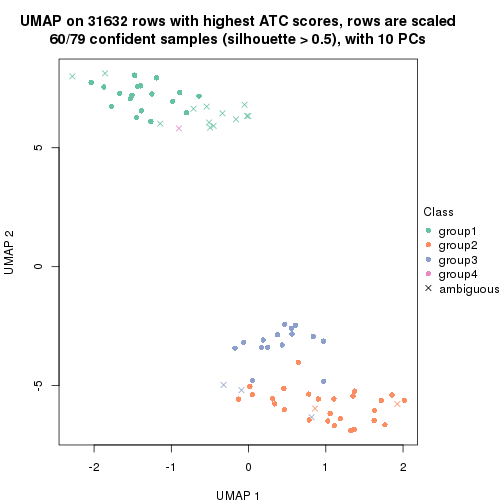
dimension_reduction(res, k = 5, method = "UMAP")
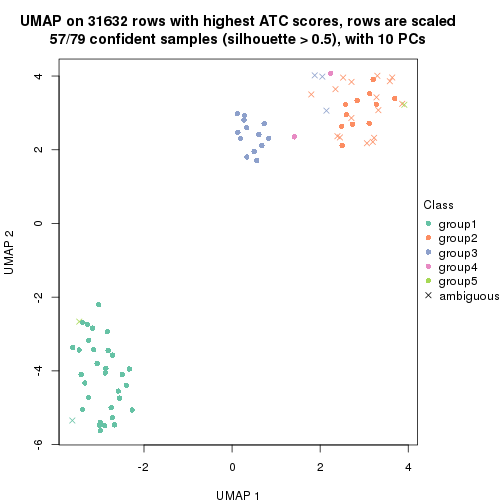
dimension_reduction(res, k = 6, method = "UMAP")
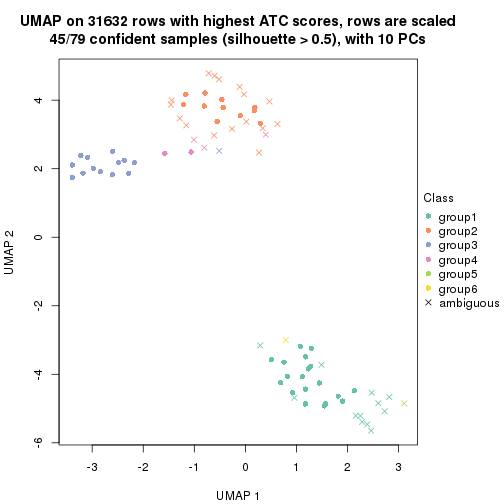
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
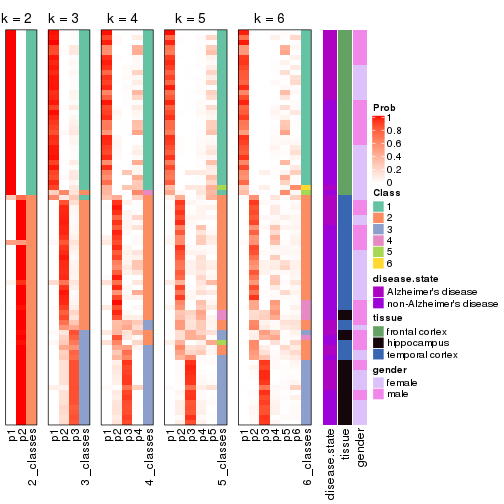
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n disease.state(p) tissue(p) gender(p) k
#> ATC:NMF 78 0.6541 1.15e-17 0.901 2
#> ATC:NMF 75 0.1800 1.21e-24 0.667 3
#> ATC:NMF 60 0.0814 3.01e-19 0.147 4
#> ATC:NMF 57 0.6542 2.96e-22 0.224 5
#> ATC:NMF 45 0.5663 3.03e-17 0.284 6
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
sessionInfo()
#> R version 3.6.0 (2019-04-26)
#> Platform: x86_64-pc-linux-gnu (64-bit)
#> Running under: CentOS Linux 7 (Core)
#>
#> Matrix products: default
#> BLAS: /usr/lib64/libblas.so.3.4.2
#> LAPACK: /usr/lib64/liblapack.so.3.4.2
#>
#> locale:
#> [1] LC_CTYPE=en_GB.UTF-8 LC_NUMERIC=C LC_TIME=en_GB.UTF-8
#> [4] LC_COLLATE=en_GB.UTF-8 LC_MONETARY=en_GB.UTF-8 LC_MESSAGES=en_GB.UTF-8
#> [7] LC_PAPER=en_GB.UTF-8 LC_NAME=C LC_ADDRESS=C
#> [10] LC_TELEPHONE=C LC_MEASUREMENT=en_GB.UTF-8 LC_IDENTIFICATION=C
#>
#> attached base packages:
#> [1] grid stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] genefilter_1.66.0 ComplexHeatmap_2.3.1 markdown_1.1 knitr_1.26
#> [5] GetoptLong_0.1.7 cola_1.3.2
#>
#> loaded via a namespace (and not attached):
#> [1] circlize_0.4.8 shape_1.4.4 xfun_0.11 slam_0.1-46
#> [5] lattice_0.20-38 splines_3.6.0 colorspace_1.4-1 vctrs_0.2.0
#> [9] stats4_3.6.0 blob_1.2.0 XML_3.98-1.20 survival_2.44-1.1
#> [13] rlang_0.4.2 pillar_1.4.2 DBI_1.0.0 BiocGenerics_0.30.0
#> [17] bit64_0.9-7 RColorBrewer_1.1-2 matrixStats_0.55.0 stringr_1.4.0
#> [21] GlobalOptions_0.1.1 evaluate_0.14 memoise_1.1.0 Biobase_2.44.0
#> [25] IRanges_2.18.3 parallel_3.6.0 AnnotationDbi_1.46.1 highr_0.8
#> [29] Rcpp_1.0.3 xtable_1.8-4 backports_1.1.5 S4Vectors_0.22.1
#> [33] annotate_1.62.0 skmeans_0.2-11 bit_1.1-14 microbenchmark_1.4-7
#> [37] brew_1.0-6 impute_1.58.0 rjson_0.2.20 png_0.1-7
#> [41] digest_0.6.23 stringi_1.4.3 polyclip_1.10-0 clue_0.3-57
#> [45] tools_3.6.0 bitops_1.0-6 magrittr_1.5 eulerr_6.0.0
#> [49] RCurl_1.95-4.12 RSQLite_2.1.4 tibble_2.1.3 cluster_2.1.0
#> [53] crayon_1.3.4 pkgconfig_2.0.3 zeallot_0.1.0 Matrix_1.2-17
#> [57] xml2_1.2.2 httr_1.4.1 R6_2.4.1 mclust_5.4.5
#> [61] compiler_3.6.0